Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T01:05:53.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Second flip in the Hassett–Keel program: existence of good moduli spaces

Part of: Algebraic groups Curves Families, fibrations

Published online by Cambridge University Press:  15 May 2017

Jarod Alper ,
Maksym Fedorchuk  and
David Ishii Smyth
Jarod Alper
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 0200, Australia email [email protected]
Maksym Fedorchuk
Affiliation:
Mathematics Department, Boston College, 140 Commonwealth Ave, Chestnut Hill, MA 02467, USA email [email protected]
David Ishii Smyth
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 0200, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

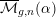We prove a general criterion for an algebraic stack to admit a good moduli space. This result may be considered as a generalization of the Keel–Mori theorem, which guarantees the existence of a coarse moduli space for a separated Deligne–Mumford stack. We apply this result to prove that the moduli stacks $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$ parameterizing 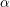$\unicode[STIX]{x1D6FC}$-stable curves introduced in [J. Alper et al., Second flip in the Hassett–Keel program: a local description, Compositio Math. 153 (2017), 1547–1583] admit good moduli spaces.

Keywords

algebraic stacksgood moduli spacesHassett–Keel program

MSC classification

Primary: 14D23: Stacks and moduli problems 14H10: Families, moduli (algebraic) 14L30: Group actions on varieties or schemes (quotients)
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 8 , August 2017 , pp. 1584 - 1609
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alper, J., On the local quotient structure of Artin stacks , J. Pure Appl. Algebra 214 (2010), 1576–1591.CrossRefGoogle Scholar
Alper, J., Good moduli spaces for Artin stacks , Ann. Inst. Fourier (Grenoble) 63 (2013), 2349–2402.Google Scholar
Alper, J., Fedorchuk, M. and Smyth, D. I., Second flip in the Hassett–Keel program: projectivity , Int. Math. Res. Not. IMRN (2016), doi:10.1093/imrn/rnw216.CrossRefGoogle Scholar
Alper, J., Fedorchuk, M., Smyth, D. I. and van der Wyck, F., Second flip in the Hassett–Keel program: a local description , Compositio Math. 153 (2017), 1547–1583.Google Scholar
Alper, J. and Kresch, A., Equivariant versal deformations of semistable curves , Michigan Math. J. 65 (2016), 227–250.Google Scholar
Hassett, B. and Hyeon, D., Log canonical models for the moduli space of curves: the first divisorial contraction , Trans. Amer. Math. Soc. 361 (2009), 4471–4489.Google Scholar
Hassett, B. and Hyeon, D., Log minimal model program for the moduli space of stable curves: the first flip , Ann. of Math. (2) 177 (2013), 911–968.Google Scholar
Keel, S. and Mori, S., Quotients by groupoids , Ann. of Math. (2) 145 (1997), 193–213.Google Scholar
Li, C., Wang, X. and Xu, C., Degeneration of Kähler–Einstein Fano manifolds, Preprint (2014), arXiv:1411.0761v2.Google Scholar
Luna, D., Slices étales , in Sur les groupes algébriques, Bulletin Société Mathématique de France, Mémoire, vol. 33 (Société Mathématique de France, Paris, 1973), 81–105.Google Scholar
Mumford, D., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Neue Folge, Band 34 (Springer, Berlin, 1965).CrossRefGoogle Scholar
Odaka, Y., Compact moduli spaces of Kähler–Einstein Fano varieties , Publ. Res. Inst. Math. Sci. 51 (2015), 549–565.Google Scholar
Smyth, D. I., Modular compactifications of the space of pointed elliptic curves I , Compositio Math. 147 (2011), 877–913.Google Scholar
Smyth, D. I., Modular compactifications of the space of pointed elliptic curves II , Compositio Math. 147 (2011), 1843–1884.Google Scholar
van der Wyck, F., Moduli of singular curves and crimping, PhD thesis, Harvard (2010).Google Scholar