Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T16:09:56.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Schemes over 𝔽1 and zeta functions

Part of: Arithmetic problems. Diophantine geometry Algebraic geometry: Foundations Arithmetic algebraic geometry

Published online by Cambridge University Press:  21 April 2010

Alain Connes  and
Caterina Consani
Alain Connes
Affiliation:
Collège de France 3, I.H.E.S. and Vanderbilt University, rue d’Ulm, Paris F-75005, France (email: [email protected])
Caterina Consani
Affiliation:
Mathematics Department, The Johns Hopkins University, Baltimore, MD 21218, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

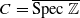We determine the real counting function N(q) (q∈[1,∞)) for the hypothetical ‘curve’ over 𝔽1, whose corresponding zeta function is the complete Riemann zeta function. We show that such a counting function exists as a distribution, is positive on (1,∞) and takes the value −∞ at q=1 as expected from the infinite genus of C. Then, we develop a theory of functorial 𝔽1-schemes which reconciles the previous attempts by Soulé and Deitmar. Our construction fits with the geometry of monoids of Kato, is no longer limited to toric varieties and it covers the case of schemes associated with Chevalley groups. Finally we show, using the monoid of adèle classes over an arbitrary global field, how to apply our functorial theory of 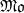-schemes to interpret conceptually the spectral realization of zeros of L-functions.

Keywords

absolute pointcounting functionszeta functions over 𝔽1𝔽1-schemesprojective adèle class spacespectral realization of zeros of L-functions

MSC classification

Secondary: 14A15: Schemes and morphisms 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Compositio Mathematica , Volume 146 , Issue 6 , November 2010 , pp. 1383 - 1415
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Connes, A., Trace formula in non-commutative geometry and the zeros of the Riemann zeta function, Selecta Math. (N.S.) 5 (1999), 29–106.Google Scholar
[2]Connes, A. and Consani, C., On the notion of geometry over 𝔽1, J. Algebraic Geom., to appear, arXiv08092926v2 [mathAG].Google Scholar
[3]Connes, A. and Consani, C., Characteristic 1, entropy and the absolute point. Preprint (2009), arXiv:MathAG0911.3537.Google Scholar
[4]Connes, A., Consani, C. and Marcolli, M., Noncommutative geometry and motives: the thermodynamics of endomotives, Adv. Math. 214 (2007), 761–831.CrossRefGoogle Scholar
[5]Connes, A., Consani, C. and Marcolli, M., The Weil proof and the geometry of the adeles class space, in Algebra, arithmetic and geometry–Manin Festschrift, Progress in Mathematics, vol. 269 (Birkhäuser, Boston, MA, 2008).Google Scholar
[6]Connes, A., Consani, C. and Marcolli, M., Fun with 𝔽1, J. Number Theory 129 (2009), 1532–1561.CrossRefGoogle Scholar
[7]Connes, A. and Marcolli, M., Noncommutative geometry, quantum fields, and motives, Colloquium Publications, vol. 55 (American Mathematical Society, Providence, RI, 2008).Google Scholar
[8]Deitmar, A., Schemes over F1, in Number fields and function fields? Two parallel worlds, Progress in Mathematics, vol. 239 eds van der Geer, G., Moonen, B. and Schoof, R. (Birkhäuser, Boston, MA, 2005).Google Scholar
[9]Deitmar, A., Remarks on zeta functions and K-theory over F1, Proc. Japan Acad. Ser. A Math. Sci. 82 (2006), 141–146.Google Scholar
[10]Deitmar, A., F1-schemes and toric varieties, Contrib. Algebra Geom. 49 (2008), 517–525.Google Scholar
[11]Demazure, M. and Gabriel, P., Groupes algébriques (Masson & CIE Éditeur, Paris, 1970).Google Scholar
[12]Demazure, M., Grothendieck, A.et al., Séminaire de Géométrie Algébrique (SGA3): Schémas en Groupes III, Lecture Notes in Mathematics, vol. 569 (Springer, Berlin, 1977).Google Scholar
[13]Gilmer, R., Commutative semigroup rings (University of Chicago Press, Chicago, IL, 1980).Google Scholar
[14]Grothendieck, A., Sur quelques points d’algèbre homologique, Tohoku Math. J. 9 (1957), 119–183.Google Scholar
[15]Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).CrossRefGoogle Scholar
[16]Ingham, A., The distribution of prime numbers, With a foreword by R. C. Vaughan, in Cambridge mathematical library (Cambridge University Press, Cambridge, 1990).Google Scholar
[17]Kapranov, M. and Smirnov, A., Cohomology determinants and reciprocity laws,http://matrix.cmi.ua.ac.be/fun/index.php/kapranovsmirnov.html.Google Scholar
[18]Kato, K., Toric singularities, Amer. J. Math. 116 (1994), 1073–1099.Google Scholar
[19]Kurokawa, N., Multiple zeta functions: an example, in Zeta functions in geometry (Tokyo, 1990), Advanced Studies in Pure Mathematics, vol. 21 (Kinokuniya, Tokyo, 1992), 219–226.Google Scholar
[20]Kurokawa, N., Ochiai, H. and Wakayama, A., Absolute derivations and zeta functions, Documenta Math., Extra Volume: Kazuya Katos Fiftieth Birthday (2003), 565–584.CrossRefGoogle Scholar
[21]Manin, Y. I., Lectures on zeta functions and motives (according to Deninger and Kurokawa) Columbia university number-theory seminar (1992), Astérisque 4 (1995), 121–163.Google Scholar
[22]Meyer, R., On a representation of the idele class group related to primes and zeros ofL-functions, Duke Math. J. 127 (2005), 519–595.CrossRefGoogle Scholar
[23]Soulé, C., Les variétés sur le corps à un élément, Mosc. Math. J. 4 (2004), 217–244.CrossRefGoogle Scholar
[24]Steinberg, R., A geometric approach to the representations of the full linear group over a Galois field, Trans. Amer. Math. Soc. 71 (1951), 274–282.CrossRefGoogle Scholar
[25]Tits, J., Sur les analogues algébriques des groupes semi-simples complexes. Colloque d’algèbre supérieure, Bruxelles 19–22 décembre 1956, in Centre Belge de Recherches Mathématiques Établissements Ceuterick (Louvain; Librairie Gauthier-Villars, Paris, 1957), 261–289.Google Scholar
[26]Töen, B. and Vaquié, M., Au dessous de Spec(ℤ), J. K-theory 3 (2009), 437–500.CrossRefGoogle Scholar