No CrossRef data available.
Article contents
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
Published online by Cambridge University Press: 24 March 2025
Abstract
Without using the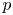 
$p$-adic Langlands correspondence, we prove that for many finite-length smooth representations of 
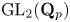$\mathrm {GL}_2(\mathbf {Q}_p)$ on 
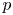$p$-torsion modules the 
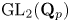$\mathrm {GL}_2(\mathbf {Q}_p)$-linear morphisms coincide with the morphisms that are linear for the normalizer of a parahoric subgroup. We identify this subgroup to be the Iwahori subgroup in the supersingular case, and 
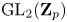$\mathrm {GL}_2(\mathbf {Z}_p)$ in the principal series case. As an application, we relate the action of parahoric subgroups to the action of the inertia group of 
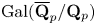$\mathrm {Gal}(\overline {\mathbf {Q}}_p/\mathbf {Q}_p)$, and we prove that if an irreducible Banach space representation 
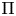$\Pi$ of 
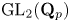$\mathrm {GL}_2(\mathbf {Q}_p)$ has infinite 
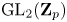$\mathrm {GL}_2(\mathbf {Z}_p)$-length, then a twist of 
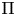$\Pi$ has locally algebraic vectors. This answers a question of Dospinescu. We make the simplifying assumption that 
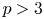$p > 3$ and that all our representations are generic.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Barthel, L. and Livné, R., Irreducible modular representations of 
${\rm GL_2}$ of a local field, Duke Math. J. 75 (1994), 261–292; MR 1290194.Google Scholar
${\rm GL_2}$ of a local field, Duke Math. J. 75 (1994), 261–292; MR 1290194.Google ScholarBreuil, C., Sur quelques représentations modulaires et $p$-adiques de ${\rm GL}_2({\rm Q}_p)$. I, Compos. Math. 138 (2003), 165–188; MR 2018825.CrossRefGoogle Scholar
$p$-adiques de 
${\rm GL}_2({\rm Q}_p)$. I, Compos. Math. 138 (2003), 165–188; MR 2018825.CrossRefGoogle ScholarBreuil, C., Sur quelques représentations modulaires et $p$-adiques de ${\rm GL}_2({\rm Q}_p)$. II, J. Inst. Math. Jussieu 2 (2003), 23–58; MR 1955206.Google Scholar
$p$-adiques de 
${\rm GL}_2({\rm Q}_p)$. II, J. Inst. Math. Jussieu 2 (2003), 23–58; MR 1955206.Google ScholarBreuil, C. and Paškūnas, V., Towards a modulo $p$ Langlands correspondence for ${\rm GL_2}$, Mem. Amer. Math. Soc. 216 (2012); MR 2931521.Google Scholar
$p$ Langlands correspondence for 
${\rm GL_2}$, Mem. Amer. Math. Soc. 216 (2012); MR 2931521.Google ScholarCasselman, W., The restriction of a representation of ${\rm GL}_{2}(k)$ to ${\rm GL}_{2}(\mathfrak {o})$, Math. Ann. 206 (1973), 311–318; MR 0338274.Google Scholar
${\rm GL}_{2}(k)$ to 
${\rm GL}_{2}(\mathfrak {o})$, Math. Ann. 206 (1973), 311–318; MR 0338274.Google ScholarColmez, P. and Dospinescu, G., Completés universels de représentations de ${\rm GL}_2(\Bbb {Q}_p)$, Algebra Number Theory 8 (2014), 1447–1519; MR 3267142.CrossRefGoogle Scholar
${\rm GL}_2(\Bbb {Q}_p)$, Algebra Number Theory 8 (2014), 1447–1519; MR 3267142.CrossRefGoogle ScholarDospinescu, G., Paškūnas, V. and Schraen, B., Infinitesimal characters in arithmetic families, Preprint (2020), arXiv:2012.01041.Google Scholar
Hu, Y. and Wang, H., On some mod $p$ representations of quaternion algebra over $\mathbb {Q}_p$, Preprint (2022), arXiv:2201.01464.Google Scholar
$p$ representations of quaternion algebra over 
$\mathbb {Q}_p$, Preprint (2022), arXiv:2201.01464.Google ScholarHu, Y. and Wang, H., On some $p$-adic and mod $p$ representations of quaternion algebra over $\mathbb {Q}_p$, J. Reine Angew. Math. 812 (2024), 163–210.Google Scholar
$p$-adic and mod 
$p$ representations of quaternion algebra over 
$\mathbb {Q}_p$, J. Reine Angew. Math. 812 (2024), 163–210.Google ScholarMorra, S., Explicit description of irreducible ${\rm GL_2}({\rm Q}_p)$-representations over $\overline {\boldsymbol F}_p$, J. Algebra 339 (2011), 252–303; MR 2811322.Google Scholar
${\rm GL_2}({\rm Q}_p)$-representations over 
$\overline {\boldsymbol F}_p$, J. Algebra 339 (2011), 252–303; MR 2811322.Google ScholarMorra, S., Invariant elements for $p$-modular representations of ${\rm GL}_2({\rm Q}_p)$, Trans. Amer. Math. Soc. 365 (2013), 6625–6667; MR 3105765.Google Scholar
$p$-modular representations of 
${\rm GL}_2({\rm Q}_p)$, Trans. Amer. Math. Soc. 365 (2013), 6625–6667; MR 3105765.Google ScholarMorra, S., Sur les atomes automorphes de longueur 2 de ${\rm GL}_2({\rm Q}_p)$, Doc. Math. 22 (2017), 777–823; MR 3650223.Google Scholar
${\rm GL}_2({\rm Q}_p)$, Doc. Math. 22 (2017), 777–823; MR 3650223.Google ScholarPaškūnas, V., Extensions for supersingular representations of ${\rm GL_2}(\mathbb {Q}_p)$, Astérisque 331 (2010), 317–353; MR 2667891.Google Scholar
${\rm GL_2}(\mathbb {Q}_p)$, Astérisque 331 (2010), 317–353; MR 2667891.Google ScholarPaškūnas, V., The image of Colmez's Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191; MR 3150248.Google Scholar
Paškūnas, V., On some consequences of a theorem of J. Ludwig, Preprint (2018), arXiv:1804.07567.Google Scholar
Serre, J.-P., Arbres, amalgames, ${\rm SL}_{2}$, Astérisque, No. 46, Société Mathématique de France, Paris, 1977, Avec un sommaire anglais, Rédigé avec la collaboration de Hyman Bass; MR 0476875.Google Scholar
${\rm SL}_{2}$, Astérisque, No. 46, Société Mathématique de France, Paris, 1977, Avec un sommaire anglais, Rédigé avec la collaboration de Hyman Bass; MR 0476875.Google ScholarVignéras, M.-F., Représentations l-modulaires d'un groupe réductif p-adique avec l ≠ p, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, MA, 1996); MR 1395151.Google Scholar