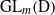Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-04T21:15:18.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Représentations banales de ${\rm GL}_{m}({\rm D})$

Part of: Lie groups

Published online by Cambridge University Press:  02 January 2013

Alberto Mínguez  and
Vincent Sécherre
Alberto Mínguez
Affiliation:
Institut de Mathématiques de Jussieu, Université Pierre et Marie Curie, 4, place Jussieu, 75005 Paris, France (email: [email protected])
Vincent Sécherre
Affiliation:
Université de Versailles Saint-Quentin-en-Yvelines, Laboratoire de Mathématiques de Versailles, 45 avenue des Etats-Unis, 78035 Versailles cedex, France (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 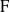${\rm F}$ be a non-Archimedean locally compact field of residue characteristic 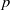$p$, let 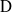${\rm D}$ be a finite-dimensional central division 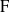${\rm F}$-algebra and let 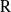${\rm R}$ be an algebraically closed field of characteristic different from 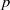$p$. We define banal irreducible 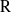${\rm R}$-representations of the group 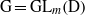${\rm G}={\rm GL}_{m}({\rm D})$. This notion involves a condition on the cuspidal support of the representation depending on the characteristic of 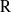${\rm R}$. When this characteristic is banal with respect to 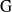${\rm G}$, in particular when 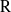${\rm R}$ is the field of complex numbers, any irreducible 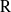${\rm R}$-representation of 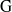${\rm G}$ is banal. In this article, we give a classification of all banal irreducible 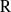${\rm R}$-representations of 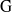${\rm G}$ in terms of certain multisegments, called banal. When 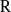${\rm R}$ is the field of complex numbers, our method provides a new proof, entirely local, of Tadić’s classification of irreducible complex smooth representations of 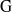${\rm G}$.

Keywords

representations of $p$-adic groupsmodular representationmultisegmentbanal representation

MSC classification

Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 679 - 704
Copyright
Copyright © 2013 The Author(s)

References

[Ari02]Ariki, S., Representations of quantum algebras and combinatorics of Young tableaux, University Lecture Series, vol. 26 (American Mathematical Society, Providence, RI, 2002).CrossRefGoogle Scholar
[Aub95]Aubert, A.-M., Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif $p$-adique, Trans. Amer. Math. Soc. 347 (1995), 2179–2189.Google Scholar
[Aub96]Aubert, A.-M., Erratum à Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif $p$-adique, Trans. Amer. Math. Soc. 348 (1996), 4687–4690.CrossRefGoogle Scholar
[Aue04]Auel, A. N., Une démonstration d’un théorème de Bernstein sur les représentations de quasi carré intégrable de ${{\rm {G}{L}}}_{n}({F})$où ${F}$est un corps local non archimédien, Mémoire de DEA, Université Paris Sud (2004).Google Scholar
[Bad04]Badulescu, A. I., Un résultat d’irréductibilité en caractéristique non nulle, Tohoku Math. J. (2) 56 (2004), 583–592.Google Scholar
[BHLS10]Badulescu, A. I., Henniart, G., Lemaire, B. and Sécherre, V., Sur le dual unitaire de ${\rm GL}_r(D)$, Amer. J. Math. 132 (2010), 1365–1396.Google Scholar
[BR07]Badulescu, A. I. and Renard, D., Zelevinsky involution and Moeglin–Waldspurger algorithm for ${\rm GL}_n(D)$, Funct. Anal. IX 48 (2007), 9–15.Google Scholar
[BZ76]Bernstein, I. N. and Zelevinsky, A. V., Representations of the group ${\rm GL}(n,F)$, where $F$ is a local non-Archimedean field, Uspehi Mat. Nauk 31 (1976), 5–70.Google Scholar
[BZ77]Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive $p$-adic groups. I, Ann. Sci. Éc. Norm. Supér 10 (1977), 441–472.Google Scholar
[CG97]Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, MA, 1997).Google Scholar
[Dat05]Dat, J.-F., $\nu $-tempered representations of $p$-adic groups, I: $l$-adic case, Duke Math. J. 126 (2005), 397–469.Google Scholar
[Dat09]Dat, J.-F., Finitude pour les représentations lisses de groupes $p$-adiques, J. Inst. Math. Jussieu 8 (2009), 261–333.CrossRefGoogle Scholar
[DKV84]Deligne, P., Kazhdan, D. and Vignéras, M.-F., Représentations des algèbres centrales simples $p$-adiques, in Representations of reductive groups over a local field (Travaux en Cours, Hermann, Paris, 1984), 33–117.Google Scholar
[Kat93]Kato, S.-I., Duality for representations of a Hecke algebra, Proc. Amer. Math. Soc. 119 (1993), 941–946.Google Scholar
[LTV99]Leclerc, B., Thibon, J.-Y. and Vasserot, E., Zelevinsky’s involution at roots of unity, J. Reine Angew. Math. 513 (1999), 33–51.CrossRefGoogle Scholar
[Min09]Mínguez, A., Sur l’irréductibilité d’une induite parabolique, J. Reine Angew. Math. 629 (2009), 107–131.Google Scholar
[MS12a]Mínguez, A. and Sécherre, V., Types modulo ℓ pour les formes intérieures de GLn sur un corps local non archimédien, Prépublication (2012).Google Scholar
[MS12b]Mínguez, A. and Sécherre, V., Représentations lisses modulo ℓ de GLm(D), Prépublication (2012).Google Scholar
[Rod82]Rodier, F., Représentations de ${\rm GL}(n,k)$ où $k$ est un corps $p$-adique, in Bourbaki seminar, Vol. 1981/1982, Astérisque, vol. 92 (Soc. Math. France, Paris, 1982), 201–218.Google Scholar
[Tad90]Tadić, M., Induced representations of ${\rm GL}(n,A)$ for $p$-adic division algebras $A$, J. Reine Angew. Math. 405 (1990), 48–77.Google Scholar
[Vig96]Vignéras, M.-F., Représentations l-modulaires d’un groupe réductif p-adique avec l≠p, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, MA, 1996).Google Scholar
[Vig97]Vignéras, M.-F., Cohomology of sheaves on the building and $R$-representations, Invent. Math. 127 (1997), 349–373.Google Scholar
[Vig04]Vignéras, M.-F., On highest Whittaker models and integral structures, in Contributions to Automorphic forms, geometry and number theory: Shalikafest 2002 (Johns Hopkins University Press, 2004), 773–801.Google Scholar
[Zel80]Zelevinsky, A. V., Induced representations of reductive ${\mathfrak {p}}$-adic groups. II. On irreducible representations of ${\rm GL}(n)$, Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 165–210.Google Scholar