Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:28:46.859Z Has data issue: false hasContentIssue false
  • English
  • Français

The remaining cases of the Kramer–Tunnell conjecture

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  29 July 2016

Kęstutis Česnavičius  and
Naoki Imai
Kęstutis Česnavičius
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA email [email protected]
Naoki Imai
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo, 153-8914, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For an elliptic curve 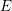$E$ over a local field 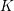$K$ and a separable quadratic extension of 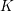$K$ , motivated by connections to the Birch and Swinnerton-Dyer conjecture, Kramer and Tunnell have conjectured a formula for computing the local root number of the base change of 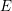$E$ to the quadratic extension in terms of a certain norm index. The formula is known in all cases except some where 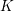$K$ is of characteristic 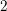$2$ , and we complete its proof by reducing the positive characteristic case to characteristic 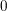$0$ . For this reduction, we exploit the principle that local fields of characteristic 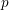$p$ can be approximated by finite extensions of 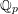$\mathbb{Q}_{p}$ : we find an elliptic curve 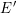$E^{\prime }$ defined over a 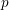$p$ -adic field such that all the terms in the Kramer–Tunnell formula for 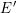$E^{\prime }$ are equal to those for 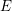$E$ .

Keywords

elliptic curvelocal fieldroot numberWeierstrass equation

MSC classification

Primary: 11G07: Elliptic curves over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 11 , November 2016 , pp. 2255 - 2268
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bushnell, C. J. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), vol. 335 (Springer, Berlin, 2006), xii+347; MR 2234120 (2007m:22013).Google Scholar
Česnavičius, K., The p-parity conjecture for elliptic curves with a p-isogeny , J. reine angew. Math. (2016), to appear. Preprint, arXiv:1207.0431.Google Scholar
Deligne, P., Courbes elliptiques: formulaire d’après J. Tate , in Modular functions of one variable, IV (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, vol. 476 (Springer, Berlin, 1975), 53–73 (French); MR 0387292 (52 #8135).Google Scholar
Deligne, P., Les corps locaux de caractéristique p, limites de corps locaux de caractéristique 0 , in Représentations des groupes réductifs sur un corps local, Travaux en Cours (Hermann, Paris, 1984), 119–157 (French); MR 771673 (86g:11068).Google Scholar
Dokchitser, T. and Dokchitser, V., Root numbers of elliptic curves in residue characteristic 2 , Bull. Lond. Math. Soc. 40 (2008), 516–524; MR 2418807 (2009k:11093).Google Scholar
Dokchitser, T. and Dokchitser, V., Root numbers and parity of ranks of elliptic curves , J. reine angew. Math. 658 (2011), 39–64; MR 2831512.Google Scholar
Dokchitser, T. and Dokchitser, V., Euler factors determine local Weil representations , J. reine angew. Math. (2016). Preprint, arXiv:1112.4889.Google Scholar
Helfgott, H. A., On the behaviour of root numbers in families of elliptic curves, Preprint (2009), arXiv:math/0408141.Google Scholar
Imai, N., Local root numbers of elliptic curves over dyadic fields , J. Math. Sci. Univ. Tokyo 22 (2015), 247–260; MR 3329196.Google Scholar
Kisin, M., Local constancy in p-adic families of Galois representations , Math. Z. 230 (1999), 569–593; MR 1680032 (2000f:14034).Google Scholar
Kramer, K. and Tunnell, J., Elliptic curves and local 𝜀-factors , Compositio Math. 46 (1982), 307–352; MR 664648 (83m:14031).Google Scholar
Rohrlich, D. E., Elliptic curves and the Weil-Deligne group , in Elliptic curves and related topics, CRM Proceedings & Lecture Notes, vol. 4 (American Mathematical Society, Providence, RI, 1994), 125–157; MR 1260960 (95a:11054).Google Scholar
Serre, J.-P., Local fields, Graduate Texts in Mathematics, vol. 67 (Springer, New York, 1979), viii+241; translated from the French by Marvin Jay Greenberg; MR 554237 (82e:12016).CrossRefGoogle Scholar
Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer, New York, 1994), xiv+525; MR 1312368 (96b:11074).Google Scholar