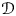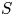1. Introduction
In this article, we are concerned with holomorphic families of coherent ![]() $\mathcal {D}$-modules on a complex manifold
$\mathcal {D}$-modules on a complex manifold ![]() $X$ of dimension
$X$ of dimension ![]() $d_X$, parametrized by a complex manifold
$d_X$, parametrized by a complex manifold ![]() $S$, that is, coherent modules over the ring
$S$, that is, coherent modules over the ring ![]() $\mathcal {D}_{X\times S/S}$ of linear relative differential operators with respect to the projection
$\mathcal {D}_{X\times S/S}$ of linear relative differential operators with respect to the projection ![]() $p_X:X\times S\rightarrow S$ (simply denoted by
$p_X:X\times S\rightarrow S$ (simply denoted by ![]() $p$ when no confusion is possible). More specifically, we consider families for which the characteristic variety in the relative cotangent space
$p$ when no confusion is possible). More specifically, we consider families for which the characteristic variety in the relative cotangent space ![]() $(T^*X)\times S$ is contained in the product by
$(T^*X)\times S$ is contained in the product by ![]() $S$ of a fixed closed conic Lagrangian analytic subset
$S$ of a fixed closed conic Lagrangian analytic subset ![]() $\Lambda \subset T^*X$. Following [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Reference Monteiro Fernandes and SabbahMFS13, Reference Monteiro Fernandes and SabbahMFS19], we call these systems relative holonomic
$\Lambda \subset T^*X$. Following [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Reference Monteiro Fernandes and SabbahMFS13, Reference Monteiro Fernandes and SabbahMFS19], we call these systems relative holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules. Here are some examples.
$\mathcal {D}_{X\times S/S}$-modules. Here are some examples.
(i) Deligne considered in [Reference DeligneDel70] the case of vector bundles
 $E$ on
$E$ on  $X\times S$ with a flat relative connection
$X\times S$ with a flat relative connection  $\nabla$, and established an equivalence with the category of locally constant sheaves of coherent
$\nabla$, and established an equivalence with the category of locally constant sheaves of coherent  $p_X^{-1}\mathcal {O}_S$-modules on
$p_X^{-1}\mathcal {O}_S$-modules on  $X\times S$. In this case, the relative characteristic variety is the product of the zero section
$X\times S$. In this case, the relative characteristic variety is the product of the zero section  $T^*_XX$ by
$T^*_XX$ by  $S$.
$S$.(ii) For any holonomic
 $\mathcal {D}_{X}$-module
$\mathcal {D}_{X}$-module  $\mathcal {M}$ on
$\mathcal {M}$ on  $X$ with characteristic variety
$X$ with characteristic variety  $\Lambda$, the pullback
$\Lambda$, the pullback  $q^*\mathcal {M}=\mathcal {O}_{X\times S}\otimes _{q^{-1}\mathcal {O}_X}q^{-1}\mathcal {M}$ by the projection
$q^*\mathcal {M}=\mathcal {O}_{X\times S}\otimes _{q^{-1}\mathcal {O}_X}q^{-1}\mathcal {M}$ by the projection  $q:X\times S\rightarrow X$ is naturally endowed with a
$q:X\times S\rightarrow X$ is naturally endowed with a  $\mathcal {D}_{X\times S/S}$-module structure, and the relative characteristic variety of
$\mathcal {D}_{X\times S/S}$-module structure, and the relative characteristic variety of  $\mathcal {M}$ is equal to
$\mathcal {M}$ is equal to  $\Lambda \times S$. For
$\Lambda \times S$. For  $(E,\nabla )$ as in example (i), the characteristic variety of
$(E,\nabla )$ as in example (i), the characteristic variety of  $q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}E$ (equipped with its natural
$q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}E$ (equipped with its natural  $\mathcal {D}_{X\times S/S}$-module structure) is contained in
$\mathcal {D}_{X\times S/S}$-module structure) is contained in  $\Lambda \times S$.
$\Lambda \times S$.(iii) Some integral transformations from objects on
 $X$ to objects on
$X$ to objects on  $S$ have kernels which are such flat bundles
$S$ have kernels which are such flat bundles  $(E,\nabla )$. One of them is the Fourier–Mukai transformation
$(E,\nabla )$. One of them is the Fourier–Mukai transformation  $\mathrm {FM}$ introduced by Laumon [Reference LaumonLau96] and Rothstein [Reference RothsteinRot96], which attaches to any bounded complex of
$\mathrm {FM}$ introduced by Laumon [Reference LaumonLau96] and Rothstein [Reference RothsteinRot96], which attaches to any bounded complex of  $\mathcal {D}$-modules with coherent cohomology on an abelian variety
$\mathcal {D}$-modules with coherent cohomology on an abelian variety  $A$ a bounded complex of
$A$ a bounded complex of  $\mathcal {O}$-modules with coherent cohomology on the moduli space
$\mathcal {O}$-modules with coherent cohomology on the moduli space  $A^\sharp$ of line bundles with integrable connection on
$A^\sharp$ of line bundles with integrable connection on  $A$ (cf. [Reference SchnellSch15] and the references therein). It is obtained as the integral transform with kernel
$A$ (cf. [Reference SchnellSch15] and the references therein). It is obtained as the integral transform with kernel  $\mathcal {P}$ on
$\mathcal {P}$ on  $A\times A^\sharp$ associated to the Poincaré bundle on the product
$A\times A^\sharp$ associated to the Poincaré bundle on the product  $A\times \mathrm {Pic}^0(A)$. By construction,
$A\times \mathrm {Pic}^0(A)$. By construction,  $\mathcal {P}$ is equipped with a flat relative connection, i.e., is a
$\mathcal {P}$ is equipped with a flat relative connection, i.e., is a  $\mathcal {D}_{A\times A^\sharp /A^\sharp }$-module. Then
$\mathcal {D}_{A\times A^\sharp /A^\sharp }$-module. Then  $q^*\mathcal {M}\otimes _{\mathcal {O}_{A\times A^\sharp }}\mathcal {P}$ is an instance of example (ii), and
$q^*\mathcal {M}\otimes _{\mathcal {O}_{A\times A^\sharp }}\mathcal {P}$ is an instance of example (ii), and  $\mathrm {FM}(\mathcal {M})$ is the pushforward
$\mathrm {FM}(\mathcal {M})$ is the pushforward  ${}_{\scriptscriptstyle \mathrm {D}}p_*(q^*\mathcal {M}\otimes _{\mathcal {O}_{A\times A^\sharp }}\mathcal {P})$. It is an object of
${}_{\scriptscriptstyle \mathrm {D}}p_*(q^*\mathcal {M}\otimes _{\mathcal {O}_{A\times A^\sharp }}\mathcal {P})$. It is an object of  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {O}_{A^\sharp })$.
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {O}_{A^\sharp })$.(iv) Given a holonomic
 $\mathcal {D}_{X}$-module
$\mathcal {D}_{X}$-module  $\mathcal {M}$ and holomorphic functions
$\mathcal {M}$ and holomorphic functions  $f_1,\ldots,f_p$ on
$f_1,\ldots,f_p$ on  $X$ defining a divisor
$X$ defining a divisor  $Y = \{\mathop {\textstyle \prod } _if_i = 0\}$, and setting
$Y = \{\mathop {\textstyle \prod } _if_i = 0\}$, and setting  $S=\mathbb {C}^p$ with coordinates
$S=\mathbb {C}^p$ with coordinates  $s_1,\ldots, s_p$, the
$s_1,\ldots, s_p$, the  $S$-analytic counterpart of [Reference MaisonobeMai23, Proposition 13] asserts that the
$S$-analytic counterpart of [Reference MaisonobeMai23, Proposition 13] asserts that the  $\mathcal {D}_{X\times S/S}$-submodule generated by
$\mathcal {D}_{X\times S/S}$-submodule generated by  $q^*\mathcal {M}\cdot (\mathop {\textstyle \prod } _if_i^{s_i})$ in the twisted coherent
$q^*\mathcal {M}\cdot (\mathop {\textstyle \prod } _if_i^{s_i})$ in the twisted coherent  $\mathcal {D}_{X\times S/S}(*(Y\times S))$-module
$\mathcal {D}_{X\times S/S}(*(Y\times S))$-module  $q^*\mathcal {M}(*(Y\times S))\cdot (\mathop {\textstyle \prod } _if_i^{s_i})$ is relative holonomic.
$q^*\mathcal {M}(*(Y\times S))\cdot (\mathop {\textstyle \prod } _if_i^{s_i})$ is relative holonomic.(v) In his construction of moduli spaces for regular holonomic
 $\mathcal {D}$-modules, Nitsure [Reference NitsureNit99] fixes a divisor with normal crossings in
$\mathcal {D}$-modules, Nitsure [Reference NitsureNit99] fixes a divisor with normal crossings in  $X$ and deforms pre-
$X$ and deforms pre- $\mathcal {D}$-modules (extending the notion of vector bundle with flat logarithmic connection) relative to this divisor and its canonical stratification. The corresponding holomorphic family of regular holonomic
$\mathcal {D}$-modules (extending the notion of vector bundle with flat logarithmic connection) relative to this divisor and its canonical stratification. The corresponding holomorphic family of regular holonomic  $\mathcal {D}$-modules has its characteristic variety adapted to this stratification, hence of the form
$\mathcal {D}$-modules has its characteristic variety adapted to this stratification, hence of the form  $\Lambda \times S$.
$\Lambda \times S$.(vi) Mixed twistor
 $\mathcal {D}$-modules (cf. [Reference MochizukiMoc15]) are compound objects defined on the product of
$\mathcal {D}$-modules (cf. [Reference MochizukiMoc15]) are compound objects defined on the product of  $X$ by the complex line
$X$ by the complex line  $\mathbb {C}$, whose module components are holomorphic families of holonomic
$\mathbb {C}$, whose module components are holomorphic families of holonomic  $\mathcal {D}$-modules parametrized by
$\mathcal {D}$-modules parametrized by  $S=\mathbb {C}^*$ degenerating at
$S=\mathbb {C}^*$ degenerating at  $0\in \mathbb {C}$ to a coherent module on the cotangent space
$0\in \mathbb {C}$ to a coherent module on the cotangent space  $T^*X$. On
$T^*X$. On  $S$, the characteristic variety of each holonomic
$S$, the characteristic variety of each holonomic  $\mathcal {D}$-module is, by definition, contained in a fixed Lagrangian variety
$\mathcal {D}$-module is, by definition, contained in a fixed Lagrangian variety  $\Lambda$. Of particular interest are the regular mixed twistor
$\Lambda$. Of particular interest are the regular mixed twistor  $\mathcal {D}$-modules, which have furnished the first example of families we are dealing with (cf. [Reference Monteiro Fernandes and SabbahMFS13]).
$\mathcal {D}$-modules, which have furnished the first example of families we are dealing with (cf. [Reference Monteiro Fernandes and SabbahMFS13]).
Our definition of relative holonomicity imposes the following: the only possible changes in the characteristic variety of the restricted ![]() $\mathcal {D}_{X}$-module to a fixed parameter, when the parameter varies, is a change of multiplicities on each irreducible component of
$\mathcal {D}_{X}$-module to a fixed parameter, when the parameter varies, is a change of multiplicities on each irreducible component of ![]() $\Lambda$. This condition is reasonable, as shown by the previous examples.
$\Lambda$. This condition is reasonable, as shown by the previous examples.
In addition, not any relative holonomic ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {K}$ can serve as the kernel of an integral transformation as in example (iii), because it cannot be ensured that, for a holonomic
$\mathcal {K}$ can serve as the kernel of an integral transformation as in example (iii), because it cannot be ensured that, for a holonomic ![]() $\mathcal {D}_{X}$-module
$\mathcal {D}_{X}$-module ![]() $\mathcal {M}$, the tensor product
$\mathcal {M}$, the tensor product ![]() $q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}\mathcal {K}$ is
$q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}\mathcal {K}$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent, in contrast with the classical result when
$\mathcal {D}_{X\times S/S}$-coherent, in contrast with the classical result when ![]() $S$ is reduced to a point. Indeed, in general, Bernstein–Sato theory only applies on some open subset of
$S$ is reduced to a point. Indeed, in general, Bernstein–Sato theory only applies on some open subset of ![]() $S$ depending on
$S$ depending on ![]() $\mathcal {M}$, as exemplified in [Reference Monteiro Fernandes and SabbahMFS17, Example 2.4]. Fortunately, adding the regularity property, as defined in [Reference Monteiro Fernandes and SabbahMFS19], of the kernel
$\mathcal {M}$, as exemplified in [Reference Monteiro Fernandes and SabbahMFS17, Example 2.4]. Fortunately, adding the regularity property, as defined in [Reference Monteiro Fernandes and SabbahMFS19], of the kernel ![]() $\mathcal {K}$ and of
$\mathcal {K}$ and of ![]() $\mathcal {M}$ overcomes this difficulty, as already shown in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] when
$\mathcal {M}$ overcomes this difficulty, as already shown in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] when ![]() $\dim S=1$.
$\dim S=1$.
In order to replace Bernstein–Sato theory, the main tool is the stability of regular holonomicity by ![]() $\mathcal {D}$-module pullback [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Theorem 2], that we generalize to the case where
$\mathcal {D}$-module pullback [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Theorem 2], that we generalize to the case where ![]() $\dim S$ can be arbitrary.
$\dim S$ can be arbitrary.
Theorem 1 (Stability by pullback)
Let ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and let
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and let ![]() $f:Y\rightarrow X$ be a morphism of complex manifolds and let us still denote by
$f:Y\rightarrow X$ be a morphism of complex manifolds and let us still denote by ![]() $f$ the morphism
$f$ the morphism ![]() $f\times \operatorname {Id}$. Then
$f\times \operatorname {Id}$. Then ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{Y\times S/S})$.
${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{Y\times S/S})$.
A possible application of our approach is that, for an integral transformation as in example (iii) with regular holonomic kernel ![]() $\mathcal {K}$, the analysis of local properties of
$\mathcal {K}$, the analysis of local properties of ![]() $q^*\mathcal {M}\otimes ^L_{\mathcal {O}_{X\times S}}\mathcal {K}$ leads to a better understanding of the
$q^*\mathcal {M}\otimes ^L_{\mathcal {O}_{X\times S}}\mathcal {K}$ leads to a better understanding of the ![]() $\mathcal {K}$-transform
$\mathcal {K}$-transform ![]() ${}_{\scriptscriptstyle \mathrm {D}}p_*(q^*\mathcal {M}\otimes ^L_{\mathcal {O}_{X\times S}}\mathcal {K})$ of
${}_{\scriptscriptstyle \mathrm {D}}p_*(q^*\mathcal {M}\otimes ^L_{\mathcal {O}_{X\times S}}\mathcal {K})$ of ![]() $\mathcal {M}$.
$\mathcal {M}$.
Here we give natural examples of regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules.
$\mathcal {D}_{X\times S/S}$-modules.
(i) Coherent
 $\mathcal {D}_{X\times S/S}$-submodules of regular holonomic
$\mathcal {D}_{X\times S/S}$-submodules of regular holonomic  $\mathcal {D}_{X\times S}$-modules, provided that the irreducible components of the characteristic variety of the latter decompose as products with respect to the product decomposition
$\mathcal {D}_{X\times S}$-modules, provided that the irreducible components of the characteristic variety of the latter decompose as products with respect to the product decomposition  $T^*X\times T^*S$ (cf. § 3.c); they can be called integrable regular holonomic
$T^*X\times T^*S$ (cf. § 3.c); they can be called integrable regular holonomic  $\mathcal {D}_{X\times S/S}$-modules.
$\mathcal {D}_{X\times S/S}$-modules.(ii) In the setting of example (iv), let us assume that
 $\mathcal {M}$ is regular holonomic. Then the coherent
$\mathcal {M}$ is regular holonomic. Then the coherent  $\mathcal {D}_{X\times S/S}(*(Y\times S))$-module
$\mathcal {D}_{X\times S/S}(*(Y\times S))$-module  $q^*\mathcal {M}(*Y\times S)\cdot \mathop {\textstyle \prod } _if_i^{s_i}$ is
$q^*\mathcal {M}(*Y\times S)\cdot \mathop {\textstyle \prod } _if_i^{s_i}$ is  $\mathcal {D}_{X\times S/S}$-regular holonomic, hence
$\mathcal {D}_{X\times S/S}$-regular holonomic, hence  $\mathcal {D}_{X\times S/S}$-coherent (cf. Example 4.36) and this enables us to recover the
$\mathcal {D}_{X\times S/S}$-coherent (cf. Example 4.36) and this enables us to recover the  $S$-analytic version of the result of Maisonobe in example (iv) when
$S$-analytic version of the result of Maisonobe in example (iv) when  $\mathcal {M}$ is regular holonomic.
$\mathcal {M}$ is regular holonomic.
We have developed in [Reference Monteiro Fernandes and SabbahMFS13] the notion of relative ![]() $\mathbb {C}$-constructible complex and relative perverse complex on
$\mathbb {C}$-constructible complex and relative perverse complex on ![]() $X\times S$, generalizing the notion of a relative local system of coherent
$X\times S$, generalizing the notion of a relative local system of coherent ![]() $p_X^{-1}\mathcal {O}_S$-modules considered by Deligne. For each stratum
$p_X^{-1}\mathcal {O}_S$-modules considered by Deligne. For each stratum ![]() $X_\alpha$ of a suitable complex stratification
$X_\alpha$ of a suitable complex stratification ![]() $(X_\alpha )$ of
$(X_\alpha )$ of ![]() $X$, each cohomology of such a complex is locally isomorphic to
$X$, each cohomology of such a complex is locally isomorphic to ![]() $p_{X_\alpha }^{-1}G_\alpha$ for some coherent
$p_{X_\alpha }^{-1}G_\alpha$ for some coherent ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $G_\alpha$. We prove here a Riemann–Hilbert correspondence for any
$G_\alpha$. We prove here a Riemann–Hilbert correspondence for any ![]() $\dim S$ (the
$\dim S$ (the ![]() $\dim S=1$ case was proved in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]).
$\dim S=1$ case was proved in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]).
Theorem 2 (Relative Riemann–Hilbert correspondence)
The functors
 \begin{align*} \operatorname{{}^\mathrm{p}Sol}_X: \operatorname{\mathsf{D}}^{\mathrm{b}}_{\mathrm{rhol}}(\mathcal{D}_{X\times S/S})&\longrightarrow \operatorname{\mathsf{D}}^\mathrm{b}_{{\mathbb{C}{-c}}}(p_X^{-1}\mathcal{O}_S) \\ \operatorname{RH}^S_X:\operatorname{\mathsf{D}}^\mathrm{b}_{{\mathbb{C}{-c}}}(p_X^{-1}\mathcal{O}_S)&\longrightarrow \operatorname{\mathsf{D}}^{\mathrm{b}}_{\mathrm{rhol}}(\mathcal{D}_{X\times S/S}) \end{align*}
\begin{align*} \operatorname{{}^\mathrm{p}Sol}_X: \operatorname{\mathsf{D}}^{\mathrm{b}}_{\mathrm{rhol}}(\mathcal{D}_{X\times S/S})&\longrightarrow \operatorname{\mathsf{D}}^\mathrm{b}_{{\mathbb{C}{-c}}}(p_X^{-1}\mathcal{O}_S) \\ \operatorname{RH}^S_X:\operatorname{\mathsf{D}}^\mathrm{b}_{{\mathbb{C}{-c}}}(p_X^{-1}\mathcal{O}_S)&\longrightarrow \operatorname{\mathsf{D}}^{\mathrm{b}}_{\mathrm{rhol}}(\mathcal{D}_{X\times S/S}) \end{align*}
are quasi-inverse equivalences of categories.
The proof of the correspondence is now made possible owing to [Reference Monteiro Fernandes and PrelliMFP21], as we construct the relative Riemann–Hilbert functor ![]() $\operatorname {RH}^S_X$ by means of the site
$\operatorname {RH}^S_X$ by means of the site ![]() $X_{\mathrm {sa}}\times S$ introduced in [Reference Monteiro Fernandes and PrelliMFP21] instead of the subanalytic site
$X_{\mathrm {sa}}\times S$ introduced in [Reference Monteiro Fernandes and PrelliMFP21] instead of the subanalytic site ![]() $X_{\mathrm {sa}}\times S_{\mathrm {sa}}$ considered in [Reference Monteiro Fernandes and PrelliMFP14] and used in [Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. The main results are the exact analogues of Theorems 2 and 1 in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] for
$X_{\mathrm {sa}}\times S_{\mathrm {sa}}$ considered in [Reference Monteiro Fernandes and PrelliMFP14] and used in [Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. The main results are the exact analogues of Theorems 2 and 1 in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] for ![]() $S$ of arbitrary dimension, with the same notation for relative regular holonomic complexes and
$S$ of arbitrary dimension, with the same notation for relative regular holonomic complexes and ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible complexes, and the same meaning for the perverse solution functor
$\mathbb {C}$-constructible complexes, and the same meaning for the perverse solution functor ![]() $\operatorname {{}^\mathrm {p}Sol}_X$. We change the order of the theorems with respect to Theorems 2 and 1 in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] because their proofs are done the other way round in the present paper.
$\operatorname {{}^\mathrm {p}Sol}_X$. We change the order of the theorems with respect to Theorems 2 and 1 in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] because their proofs are done the other way round in the present paper.
The strategy for the proof of these theorems is similar to that of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]: it is made precise in §§ 4.e and 6. However, when ![]() $\dim S\geqslant 2$, we have to distinguish between
$\dim S\geqslant 2$, we have to distinguish between ![]() $S$-torsion-freeness and
$S$-torsion-freeness and ![]() $S$-flatness (also called strictness in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]). Although this is not much trouble for some of the results, owing to the analysis of t-structures made in [Reference Fiorot and Monteiro FernandesFMF18], we are led to using Rossi's flattening theorem of [Reference RossiRos68] at some point.
$S$-flatness (also called strictness in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]). Although this is not much trouble for some of the results, owing to the analysis of t-structures made in [Reference Fiorot and Monteiro FernandesFMF18], we are led to using Rossi's flattening theorem of [Reference RossiRos68] at some point.
Along the way, we complement the results of [Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] by giving further characterizations and properties of regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules or objects of the bounded derived category
$\mathcal {D}_{X\times S/S}$-modules or objects of the bounded derived category ![]() $\operatorname {\mathsf {D}}^{\mathrm {b}}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, which are needed for the proof.
$\operatorname {\mathsf {D}}^{\mathrm {b}}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, which are needed for the proof.
Comparison with other works on regular holonomic  $\mathcal {D}$-modules with parameters
$\mathcal {D}$-modules with parameters
(i) In [Reference D'Agnolo, Guillermou and SchapiraDGS11], the authors introduced a formal parameter ![]() $\hbar$ and the corresponding rings
$\hbar$ and the corresponding rings ![]() $\mathbb {C}[\![\hbar ]\!]$,
$\mathbb {C}[\![\hbar ]\!]$, ![]() $\mathcal {O}_X[\![\hbar ]\!]$,
$\mathcal {O}_X[\![\hbar ]\!]$, ![]() $\mathcal {D}_{X}[\![\hbar ]\!]$ denoted by
$\mathcal {D}_{X}[\![\hbar ]\!]$ denoted by ![]() $\mathcal {D}_{X}^\hbar$. They define the notion of regular holonomic
$\mathcal {D}_{X}^\hbar$. They define the notion of regular holonomic ![]() $\mathcal {D}_{X}^\hbar$-module by asking that the restriction to the closed point
$\mathcal {D}_{X}^\hbar$-module by asking that the restriction to the closed point ![]() $\hbar =0$ is a regular holonomic
$\hbar =0$ is a regular holonomic ![]() $\mathcal {D}_{X}$-module which is different from our point of view because we ask for regular holonomicity at any value of the parameter. They proved a Riemann–Hilbert correspondence with the category of
$\mathcal {D}_{X}$-module which is different from our point of view because we ask for regular holonomicity at any value of the parameter. They proved a Riemann–Hilbert correspondence with the category of ![]() $\mathbb {C}$-constructible complexes of
$\mathbb {C}$-constructible complexes of ![]() $\mathbb {C}_X[\![\hbar ]\!]$-modules by means of a functor they denote by
$\mathbb {C}_X[\![\hbar ]\!]$-modules by means of a functor they denote by ![]() $\operatorname {TH}_\hbar$, which would correspond to the notation
$\operatorname {TH}_\hbar$, which would correspond to the notation ![]() $\operatorname {RH}_X^S$ in the present paper. The main difference with the notions introduced in the present paper (or more precisely with those introduced in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21], which only considered the case where
$\operatorname {RH}_X^S$ in the present paper. The main difference with the notions introduced in the present paper (or more precisely with those introduced in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21], which only considered the case where ![]() $\dim S=1$) is that the sheaves considered in [Reference D'Agnolo, Guillermou and SchapiraDGS11] are sheaves of
$\dim S=1$) is that the sheaves considered in [Reference D'Agnolo, Guillermou and SchapiraDGS11] are sheaves of ![]() $\mathbb {C}[\![\hbar ]\!]$-modules on
$\mathbb {C}[\![\hbar ]\!]$-modules on ![]() $X$, whereas we consider sheaves of
$X$, whereas we consider sheaves of ![]() $p_X^{-1}\mathcal {O}_S$-modules on the product space
$p_X^{-1}\mathcal {O}_S$-modules on the product space ![]() $X\times S$. The authors also considered the restriction at the generic point of
$X\times S$. The authors also considered the restriction at the generic point of ![]() $\mathbb {C}[\![\hbar ]\!]$, that is, modules over the ring
$\mathbb {C}[\![\hbar ]\!]$, that is, modules over the ring ![]() $\mathcal {D}_{X}(\!(\hbar )\!)$ which has no counterpart in our setting.
$\mathcal {D}_{X}(\!(\hbar )\!)$ which has no counterpart in our setting.
(ii) If instead of considering ![]() $\mathcal {D}_{X}$-modules one considers flat meromorphic bundles on
$\mathcal {D}_{X}$-modules one considers flat meromorphic bundles on ![]() $X$ (i.e., meromorphic connections) with fixed pole divisor, there are many works in the algebraic or formal setting, with base fields or rings that can be different from
$X$ (i.e., meromorphic connections) with fixed pole divisor, there are many works in the algebraic or formal setting, with base fields or rings that can be different from ![]() $\mathbb {C}$. As the literature is vast, let us only mention [Reference André, Baldassarri and CailottoABC20] and the more recent preprint [Reference Hai, dos Santos and TâmHdST21]. In the latter preprint, the authors extend Deligne's equivalence result [Reference DeligneDel70, Theorem II.5.9] to an equivalence with a formal parameter. The corresponding equivalence in the present article would be that for
$\mathbb {C}$. As the literature is vast, let us only mention [Reference André, Baldassarri and CailottoABC20] and the more recent preprint [Reference Hai, dos Santos and TâmHdST21]. In the latter preprint, the authors extend Deligne's equivalence result [Reference DeligneDel70, Theorem II.5.9] to an equivalence with a formal parameter. The corresponding equivalence in the present article would be that for ![]() $\mathcal {D}_{X\times S/S}$-modules of D-type, as defined in § 4.
$\mathcal {D}_{X\times S/S}$-modules of D-type, as defined in § 4.
(iii) Wu [Reference WuWu21] has established a Riemann–Hilbert correspondence similar to that of Theorem 2 in the case of Alexander complexes that occur in example (iv).
Organization of the paper
In § 2, we review and complete various results on coherent ![]() $\mathcal {D}_{X\times S/S}$-modules obtained in our previous works [Reference Monteiro Fernandes and SabbahMFS13, Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot and Monteiro FernandesFMF18, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. We emphasize the behavior of holonomicity with respect to pullback and proper pushforward both with respect to
$\mathcal {D}_{X\times S/S}$-modules obtained in our previous works [Reference Monteiro Fernandes and SabbahMFS13, Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot and Monteiro FernandesFMF18, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. We emphasize the behavior of holonomicity with respect to pullback and proper pushforward both with respect to ![]() $X$ and to the parameter space
$X$ and to the parameter space ![]() $S$. Note that the parameter space
$S$. Note that the parameter space ![]() $S$ is always assumed to be a complex manifold, whereas one should be able to generalize various statements to any complex analytic space. For example, the sheaf
$S$ is always assumed to be a complex manifold, whereas one should be able to generalize various statements to any complex analytic space. For example, the sheaf ![]() $\mathcal {D}_{X\times T/T}$ is well-defined if
$\mathcal {D}_{X\times T/T}$ is well-defined if ![]() $T$ is a possibly singular and non-reduced complex analytic space with sheaf of functions
$T$ is a possibly singular and non-reduced complex analytic space with sheaf of functions ![]() $\mathcal {O}_T$. In this work, we restrict the setting to those complex spaces
$\mathcal {O}_T$. In this work, we restrict the setting to those complex spaces ![]() $T$ that are embeddable in a smooth complex manifold
$T$ that are embeddable in a smooth complex manifold ![]() $S$, with ideal
$S$, with ideal ![]() $\mathcal {I}_T\subset \mathcal {O}_S$, and we regard
$\mathcal {I}_T\subset \mathcal {O}_S$, and we regard ![]() $\mathcal {D}_{X\times T/T}$-modules as
$\mathcal {D}_{X\times T/T}$-modules as ![]() $\mathcal {D}_{X\times S/S}$-modules annihilated by
$\mathcal {D}_{X\times S/S}$-modules annihilated by ![]() $\mathcal {I}_T$.
$\mathcal {I}_T$.
In § 3, we complement various results of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] on the regularity property. In particular, we give details on [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Remark 1.11]. Furthermore, the relation with the usual notion of regularity of holonomic ![]() $\mathcal {D}_{X\times S}$-modules is made precise in § 3.c. Stability under base pullback and proper base pushforward is established in § 3.b (as usual, under a goodness assumption for proper pushforward). The case of pushforward with respect to a proper morphism
$\mathcal {D}_{X\times S}$-modules is made precise in § 3.c. Stability under base pullback and proper base pushforward is established in § 3.b (as usual, under a goodness assumption for proper pushforward). The case of pushforward with respect to a proper morphism ![]() $f:X\rightarrow Y$ (with a goodness assumption) has already been treated in [Reference Monteiro Fernandes and SabbahMFS19], and stability by pullback, which is the content of Theorem 1 needs first a detailed analysis of holonomic
$f:X\rightarrow Y$ (with a goodness assumption) has already been treated in [Reference Monteiro Fernandes and SabbahMFS19], and stability by pullback, which is the content of Theorem 1 needs first a detailed analysis of holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules of D-type.
$\mathcal {D}_{X\times S/S}$-modules of D-type.
This analysis is performed in § 4. The reasoning made in [Reference Monteiro Fernandes and SabbahMFS19] when ![]() $\dim S=1$, relying on the property that the torsion-free quotient of a coherent
$\dim S=1$, relying on the property that the torsion-free quotient of a coherent ![]() $\mathcal {O}_S$-module is locally free, has to be adapted by using base changes with respect to
$\mathcal {O}_S$-module is locally free, has to be adapted by using base changes with respect to ![]() $S$, so that the base functoriality properties considered in §§ 2 and 3 are most useful. Theorem 1 is proved in § 4.e in a way similar to that done in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. In § 4.f, we give a characterization of relative regular holonomicity in terms of formal solutions.
$S$, so that the base functoriality properties considered in §§ 2 and 3 are most useful. Theorem 1 is proved in § 4.e in a way similar to that done in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21]. In § 4.f, we give a characterization of relative regular holonomicity in terms of formal solutions.
Section 6 gives details on the main steps of the proof of Theorem 2. The strategy is similar to that in [Reference Monteiro Fernandes and SabbahMFS19], although we need various new technical details contained in § 5. On the one hand, the construction of the Riemann–Hilbert functor ![]() $\operatorname {RH}_X^S$ is now performed by using the partial subanalytic site
$\operatorname {RH}_X^S$ is now performed by using the partial subanalytic site ![]() $X_{\mathrm {sa}}\times S$ introduced in [Reference Monteiro Fernandes and PrelliMFP21]. On the other hand, the comparison between two definitions of Deligne's extension, one using the standard notion of moderate growth and the other obtained via the complex of tempered holomorphic functions on the partial subanalytic site
$X_{\mathrm {sa}}\times S$ introduced in [Reference Monteiro Fernandes and PrelliMFP21]. On the other hand, the comparison between two definitions of Deligne's extension, one using the standard notion of moderate growth and the other obtained via the complex of tempered holomorphic functions on the partial subanalytic site ![]() $X_{\mathrm {sa}}\times S$, is also done in § 5, relying once more on results of [Reference Monteiro Fernandes and PrelliMFP21]. We emphasize that the proof given here is simpler, when
$X_{\mathrm {sa}}\times S$, is also done in § 5, relying once more on results of [Reference Monteiro Fernandes and PrelliMFP21]. We emphasize that the proof given here is simpler, when ![]() $\dim S=1$, than that given in [Reference Monteiro Fernandes and SabbahMFS19].
$\dim S=1$, than that given in [Reference Monteiro Fernandes and SabbahMFS19].
2. A review on relative coherent and holonomic  $\mathcal {D}$-modules
$\mathcal {D}$-modules
For complex analytic manifolds ![]() $X$ and
$X$ and ![]() $S$, we denote the projections by
$S$, we denote the projections by
and we use the notation ![]() $p,q$ when there is no confusion possible. The sheaf of relative differential operators
$p,q$ when there is no confusion possible. The sheaf of relative differential operators ![]() $\mathcal {D}_{X\times S/S}$ is naturally defined as
$\mathcal {D}_{X\times S/S}$ is naturally defined as
2.a Coherence, goodness, and holonomicity
We adapt the definitions of [Reference KashiwaraKas03, § 4.7], which we refer to for properties and proofs.
Definition 2.2 We say that an ![]() $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module ![]() $\mathcal {F}$ is:
$\mathcal {F}$ is:
(i)
 $\mathcal {O}$-good on
$\mathcal {O}$-good on  $X\times S$ if, on any relatively compact open set
$X\times S$ if, on any relatively compact open set  $U$ of
$U$ of  $X\times S$,
$X\times S$,  $\mathcal {F}_{|U}$ is the direct limit of an increasing sequence of
$\mathcal {F}_{|U}$ is the direct limit of an increasing sequence of  $\mathcal {O}_U$-coherent submodules (equivalently, the direct limit of an inductive system of
$\mathcal {O}_U$-coherent submodules (equivalently, the direct limit of an inductive system of  $\mathcal {O}_U$-coherent modules);
$\mathcal {O}_U$-coherent modules);(ii)
 $\mathcal {O}$-quasi-coherent if each point of
$\mathcal {O}$-quasi-coherent if each point of  $X\times S$ has an open neighborhood
$X\times S$ has an open neighborhood  $U$ on which
$U$ on which  $\mathcal {F}$ is
$\mathcal {F}$ is  $\mathcal {O}$-good.
$\mathcal {O}$-good.
We say that a ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ is:
$\mathcal {M}$ is:
(iii) good on
 $X\times S$ if it is
$X\times S$ if it is  $\mathcal {O}$-good on
$\mathcal {O}$-good on  $X\times S$ and
$X\times S$ and  $\mathcal {D}_{X\times S/S}$-coherent.
$\mathcal {D}_{X\times S/S}$-coherent.
The category ![]() $\mathrm {Mod}_{\mathcal {O} {-}\mathrm {q} {-}\mathrm {coh}}(\mathcal {O}_{X\times S})$ of
$\mathrm {Mod}_{\mathcal {O} {-}\mathrm {q} {-}\mathrm {coh}}(\mathcal {O}_{X\times S})$ of ![]() $\mathcal {O}$-quasi-coherent
$\mathcal {O}$-quasi-coherent ![]() $\mathcal {O}_{X\times S}$-modules is an abelian full subcategory of
$\mathcal {O}_{X\times S}$-modules is an abelian full subcategory of ![]() $\mathrm {Mod}(\mathcal {O}_{X\times S})$ closed under extensions. Let
$\mathrm {Mod}(\mathcal {O}_{X\times S})$ closed under extensions. Let ![]() $Y$ be a hypersurface of
$Y$ be a hypersurface of ![]() $X$. We denote by
$X$. We denote by ![]() $\bullet(*Y)$, instead of
$\bullet(*Y)$, instead of ![]() $\bullet(*(Y\times S))$, the localization functor along the hypersurface
$\bullet(*(Y\times S))$, the localization functor along the hypersurface ![]() $Y\times S$ of
$Y\times S$ of ![]() $X\times S$. We use the notation
$X\times S$. We use the notation ![]() $X^*=X\smallsetminus Y$.
$X^*=X\smallsetminus Y$.
Lemma 2.3
(i) Let
 $\mathcal {L}$ be an
$\mathcal {L}$ be an  $\mathcal {O}$-quasi-coherent module. Then
$\mathcal {O}$-quasi-coherent module. Then  $\mathcal {L}(*Y)$ is
$\mathcal {L}(*Y)$ is  $\mathcal {O}$-quasi-coherent.
$\mathcal {O}$-quasi-coherent.(ii) Let
 $\mathcal {L}$ be an
$\mathcal {L}$ be an  $\mathcal {O}$-quasi-coherent module supported on
$\mathcal {O}$-quasi-coherent module supported on  $Y\times S$ and localized along
$Y\times S$ and localized along  $Y\times S$ (i.e.,
$Y\times S$ (i.e.,  $\mathcal {L}\simeq \mathcal {L}(*Y)$). Then
$\mathcal {L}\simeq \mathcal {L}(*Y)$). Then  $\mathcal {L}=0$.
$\mathcal {L}=0$.(iii) Let
 $\mathcal {M}\stackrel {\phi }{\longrightarrow } \mathcal {N}$ be a morphism of
$\mathcal {M}\stackrel {\phi }{\longrightarrow } \mathcal {N}$ be a morphism of  $\mathcal {O}$-quasi-coherent modules which are localized along
$\mathcal {O}$-quasi-coherent modules which are localized along  $Y\times S$. If the restriction of
$Y\times S$. If the restriction of  $\phi$ at
$\phi$ at  $X^*\times S$ is an isomorphism (respectively, zero), then
$X^*\times S$ is an isomorphism (respectively, zero), then  $\phi$ is an isomorphism (respectively, zero).
$\phi$ is an isomorphism (respectively, zero).
Proof. (i) By definition, any point of ![]() $X\times S$ has an open neighborhood
$X\times S$ has an open neighborhood ![]() $U$, which we can suppose to be a relatively compact open set, on which
$U$, which we can suppose to be a relatively compact open set, on which ![]() $\mathcal {L}_{|U} = \mathop {\textstyle \bigcup } _i\mathcal {L}_i$ is the direct limit of an increasing sequence of
$\mathcal {L}_{|U} = \mathop {\textstyle \bigcup } _i\mathcal {L}_i$ is the direct limit of an increasing sequence of ![]() $\mathcal {O}$-coherent submodules
$\mathcal {O}$-coherent submodules ![]() $\mathcal {L}_i$. As
$\mathcal {L}_i$. As ![]() $\mathcal {L}_i(*Y)$, being equal to
$\mathcal {L}_i(*Y)$, being equal to ![]() $\mathop {\textstyle \bigcup } _n\mathcal {I}_{Y\times S}^{-n}\mathcal {L}_i$, is
$\mathop {\textstyle \bigcup } _n\mathcal {I}_{Y\times S}^{-n}\mathcal {L}_i$, is ![]() $\mathcal {O}$-quasi-coherent for every
$\mathcal {O}$-quasi-coherent for every ![]() $i$, so is
$i$, so is ![]() $\mathcal {L}_{|U}(*Y)=\mathop {\textstyle \bigcup } _i\mathcal {L}_i(*Y)$.
$\mathcal {L}_{|U}(*Y)=\mathop {\textstyle \bigcup } _i\mathcal {L}_i(*Y)$.
(ii) The question is local. As ![]() $\mathcal {L}$ is an
$\mathcal {L}$ is an ![]() $\mathcal {O}$-quasi-coherent module supported on
$\mathcal {O}$-quasi-coherent module supported on ![]() $Y\times S$, we can suppose (up to shrinking the neighborhood) that it is a direct limit
$Y\times S$, we can suppose (up to shrinking the neighborhood) that it is a direct limit ![]() $\mathcal {L} = \mathop {\textstyle \bigcup } _i\mathcal {L}_i$ of an increasing sequence of
$\mathcal {L} = \mathop {\textstyle \bigcup } _i\mathcal {L}_i$ of an increasing sequence of ![]() $\mathcal {O}$-coherent submodules
$\mathcal {O}$-coherent submodules ![]() $\mathcal {L}_i$ which are supported on
$\mathcal {L}_i$ which are supported on ![]() $Y\times S$. Therefore,
$Y\times S$. Therefore, ![]() $\mathcal {L}_i(*Y)=0$ for every
$\mathcal {L}_i(*Y)=0$ for every ![]() $i$ and, thus,
$i$ and, thus, ![]() $\mathcal {L}(*Y)=\mathop {\textstyle \bigcup } _i\mathcal {L}_i(*Y)=0$.
$\mathcal {L}(*Y)=\mathop {\textstyle \bigcup } _i\mathcal {L}_i(*Y)=0$.
(iii) Let us denote by ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $\mathcal {L}'$ the kernel and the cokernel of
$\mathcal {L}'$ the kernel and the cokernel of ![]() $\phi$, respectively. They are
$\phi$, respectively. They are ![]() $\mathcal {O}$-quasi-coherent modules. If the restriction of
$\mathcal {O}$-quasi-coherent modules. If the restriction of ![]() $\phi$ to
$\phi$ to ![]() $X^*\times S$ is an isomorphism, they are supported on
$X^*\times S$ is an isomorphism, they are supported on ![]() $Y\times S$. By applying the localization functor along
$Y\times S$. By applying the localization functor along ![]() $Y$, we get the following exact sequence of
$Y$, we get the following exact sequence of ![]() $\mathcal {O}$-quasi-coherent modules (by the first point)
$\mathcal {O}$-quasi-coherent modules (by the first point)
By hypothesis, ![]() $\mathcal {M}(*Y)\simeq \mathcal {M}$ and
$\mathcal {M}(*Y)\simeq \mathcal {M}$ and ![]() $\mathcal {N}(*Y)\simeq \mathcal {N}$, thus
$\mathcal {N}(*Y)\simeq \mathcal {N}$, thus ![]() $\mathcal {L}(*Y)\simeq \mathcal {L}$,
$\mathcal {L}(*Y)\simeq \mathcal {L}$, ![]() $\mathcal {L}'(*Y)\simeq \mathcal {L}'$ and by the previous point
$\mathcal {L}'(*Y)\simeq \mathcal {L}'$ and by the previous point ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $\mathcal {L}'$ are zero. If
$\mathcal {L}'$ are zero. If ![]() $\phi _{|X^*\times S}$ is zero, then
$\phi _{|X^*\times S}$ is zero, then ![]() $\mathcal {L}\rightarrow \mathcal {M}$ is an isomorphism on
$\mathcal {L}\rightarrow \mathcal {M}$ is an isomorphism on ![]() $X^*\times S$, hence it is an isomorphism and so
$X^*\times S$, hence it is an isomorphism and so ![]() $\phi$ is zero.
$\phi$ is zero.
Let ![]() $\mathcal {D}_{X\times S/S}(*Y)$ be the coherent sheaf of rings
$\mathcal {D}_{X\times S/S}(*Y)$ be the coherent sheaf of rings ![]() $\mathcal {O}_{X\times S}(*Y)\otimes _{\mathcal {O}_{X\times S}}\mathcal {D}_{X\times S/S}$. Then any coherent
$\mathcal {O}_{X\times S}(*Y)\otimes _{\mathcal {O}_{X\times S}}\mathcal {D}_{X\times S/S}$. Then any coherent ![]() $\mathcal {D}_{X\times S/S}$- or
$\mathcal {D}_{X\times S/S}$- or ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module is
$\mathcal {D}_{X\times S/S}(*Y)$-module is ![]() $\mathcal {O}$-quasi-coherent. On the other hand, any
$\mathcal {O}$-quasi-coherent. On the other hand, any ![]() $\mathcal {O}$-quasi-coherent
$\mathcal {O}$-quasi-coherent ![]() $\mathcal {D}_{X\times S/S}$-submodule
$\mathcal {D}_{X\times S/S}$-submodule ![]() $\mathcal {N}$ of a coherent
$\mathcal {N}$ of a coherent ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent. The next lemma follows by an easy adaptation of [Reference KashiwaraKas03, Proposition 4.23].
$\mathcal {D}_{X\times S/S}$-coherent. The next lemma follows by an easy adaptation of [Reference KashiwaraKas03, Proposition 4.23].
Lemma 2.4
(i) The category of coherent, respectively,
 $\mathcal {O}$-good,
$\mathcal {O}$-good,  $\mathcal {D}_{X\times S/S}$-modules, is abelian and stable by extensions in
$\mathcal {D}_{X\times S/S}$-modules, is abelian and stable by extensions in  $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$, and
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$, and  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$, respectively,
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$, respectively,  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {good}(\mathcal {D}_{X\times S/S})$, is a triangulated full subcategory of
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {good}(\mathcal {D}_{X\times S/S})$, is a triangulated full subcategory of  $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$.
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$.(ii) Let
 $\mathcal {M}^\bullet$ be a bounded complex of
$\mathcal {M}^\bullet$ be a bounded complex of  $\mathcal {O}$-good
$\mathcal {O}$-good  $\mathcal {D}_{X\times S/S}$-modules. Then each cohomology
$\mathcal {D}_{X\times S/S}$-modules. Then each cohomology  $\mathcal {H}^\ell (\mathcal {M}^\bullet)$ is
$\mathcal {H}^\ell (\mathcal {M}^\bullet)$ is  $\mathcal {O}$-good on
$\mathcal {O}$-good on  $X\times S$.
$X\times S$.(iii) On any relatively compact open subset
 $U \Subset X\times S$, each good
$U \Subset X\times S$, each good  $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module  $\mathcal {N}$ comes in an exact sequence
with
$\mathcal {N}$ comes in an exact sequence
with \[ 0\longrightarrow\mathcal{N}'\longrightarrow\mathcal{D}_{X\times S/S}\otimes_{\mathcal{O}_{X\times S}}\mathcal{L}\longrightarrow\mathcal{N}_{|U}\longrightarrow0, \]
\[ 0\longrightarrow\mathcal{N}'\longrightarrow\mathcal{D}_{X\times S/S}\otimes_{\mathcal{O}_{X\times S}}\mathcal{L}\longrightarrow\mathcal{N}_{|U}\longrightarrow0, \]
 $\mathcal {L}$ being
$\mathcal {L}$ being  $\mathcal {O}_U$-coherent and
$\mathcal {O}_U$-coherent and  $\mathcal {N}'$ being good on
$\mathcal {N}'$ being good on  $U$. In particular,
$U$. In particular,  $\mathcal {N}_{|U}$ has a coherent
$\mathcal {N}_{|U}$ has a coherent  $F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$-filtration.
$F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$-filtration.
Remark 2.5 (i) With a slight adaptation of the proof of Lemma 2.3(i) we conclude that if ![]() $\mathcal {M}$ is good (respectively,
$\mathcal {M}$ is good (respectively, ![]() $\mathcal {D}_{X\times S/S}$-coherent), then
$\mathcal {D}_{X\times S/S}$-coherent), then ![]() $\mathcal {M}(*Y)$ is
$\mathcal {M}(*Y)$ is ![]() $\mathcal {O}$-good (respectively,
$\mathcal {O}$-good (respectively, ![]() $\mathcal {O}$-quasi-coherent).
$\mathcal {O}$-quasi-coherent).
(ii) If a local section ![]() $m$ of an
$m$ of an ![]() $\mathcal {O}$-quasi-coherent module satisfying
$\mathcal {O}$-quasi-coherent module satisfying ![]() $\mathcal {M}=\mathcal {M}(*Y)$ is zero when restricted to
$\mathcal {M}=\mathcal {M}(*Y)$ is zero when restricted to ![]() $X^*\times S$, then it is zero. Indeed if
$X^*\times S$, then it is zero. Indeed if ![]() $m$ is defined on
$m$ is defined on ![]() $U\times U_S$,
$U\times U_S$, ![]() $m$ generates an
$m$ generates an ![]() $\mathcal {O}$-coherent submodule of
$\mathcal {O}$-coherent submodule of ![]() $\mathcal {M}(*Y)_{|U\times U_S}$ which is supported on
$\mathcal {M}(*Y)_{|U\times U_S}$ which is supported on ![]() $Y\times S$; given a local defining equation
$Y\times S$; given a local defining equation ![]() $f=0$ for
$f=0$ for ![]() $Y$, we have
$Y$, we have ![]() $f^km=0$ for some
$f^km=0$ for some ![]() $k$, thus
$k$, thus ![]() $m=0$.
$m=0$.
Characteristic varieties
To any object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ is associated, by means of local coherent
$\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ is associated, by means of local coherent ![]() $\mathcal {O}_{X\times S}$-filtrations, its characteristic variety
$\mathcal {O}_{X\times S}$-filtrations, its characteristic variety ![]() $\operatorname {Char}(\mathcal {M})$, which is contained in
$\operatorname {Char}(\mathcal {M})$, which is contained in ![]() $T^*X\times S$. A coherent
$T^*X\times S$. A coherent ![]() $\mathcal {D}_{X\times S/S}$-module is holonomic if its characteristic variety is contained in
$\mathcal {D}_{X\times S/S}$-module is holonomic if its characteristic variety is contained in ![]() $\Lambda \times S$, with
$\Lambda \times S$, with ![]() $\Lambda$ closed complex analytic Lagrangian
$\Lambda$ closed complex analytic Lagrangian ![]() $\mathbb {C}^*$-homogeneous in
$\mathbb {C}^*$-homogeneous in ![]() $T^*X$. The derived categories
$T^*X$. The derived categories ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ and
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ and ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})$ and the characteristic variety
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})$ and the characteristic variety ![]() $\operatorname {Char}(\mathcal {M})$ for such objects
$\operatorname {Char}(\mathcal {M})$ for such objects ![]() $\mathcal {M}$ are defined correspondingly.
$\mathcal {M}$ are defined correspondingly.
The structure of the characteristic variety of a holonomic ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ is described in [Reference Fiorot and Monteiro FernandesFMF18, Lemma 2.10]: for each irreducible component
$\mathcal {M}$ is described in [Reference Fiorot and Monteiro FernandesFMF18, Lemma 2.10]: for each irreducible component ![]() $\Lambda _i$ of
$\Lambda _i$ of ![]() $\Lambda$ (
$\Lambda$ (![]() $i\in I$) there exists a locally finite family
$i\in I$) there exists a locally finite family ![]() $(T_{ij})_{j\in J_i}$ of closed analytic subsets of
$(T_{ij})_{j\in J_i}$ of closed analytic subsets of ![]() $S$ such that
$S$ such that
The projection to ![]() $X$ of
$X$ of ![]() $\Lambda _i$ is an irreducible closed analytic subset of
$\Lambda _i$ is an irreducible closed analytic subset of ![]() $X$ that we denote by
$X$ that we denote by ![]() $Z_i$. These subsets form a locally finite family of closed analytic subsets of
$Z_i$. These subsets form a locally finite family of closed analytic subsets of ![]() $X$. We have
$X$. We have
and we set
that we call the ![]() $X$-support (which is a closed analytic subset of
$X$-support (which is a closed analytic subset of ![]() $X$) and the
$X$) and the ![]() $S$-support of
$S$-support of ![]() $\mathcal {M}$ (which may be not closed analytic if
$\mathcal {M}$ (which may be not closed analytic if ![]() $I$ is infinite), respectively. Anyway, we set
$I$ is infinite), respectively. Anyway, we set ![]() $\dim \operatorname {Supp}_S(\mathcal {M})=\max _{i,j}\dim T_{ij}\leqslant \dim S$.
$\dim \operatorname {Supp}_S(\mathcal {M})=\max _{i,j}\dim T_{ij}\leqslant \dim S$.
Any ![]() $\mathcal {D}_{X\times S/S}$-coherent submodule or quotient module of
$\mathcal {D}_{X\times S/S}$-coherent submodule or quotient module of ![]() $\mathcal {M}$ is holonomic and its characteristic variety is the union of some irreducible components of
$\mathcal {M}$ is holonomic and its characteristic variety is the union of some irreducible components of ![]() $\operatorname {Char}(\mathcal {M})$.
$\operatorname {Char}(\mathcal {M})$.
Lemma 2.8 The category ![]() $\mathrm {Mod}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ of holonomic
$\mathrm {Mod}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ of holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules is closed under taking extensions in the category
$\mathcal {D}_{X\times S/S}$-modules is closed under taking extensions in the category ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$, and under taking sub-quotients in the category
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$, and under taking sub-quotients in the category ![]() $\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$.
$\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$.
We say that a local section ![]() $m$ of a
$m$ of a ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ is an
$\mathcal {M}$ is an ![]() $S$-torsion section if it is annihilated by some holomorphic function on
$S$-torsion section if it is annihilated by some holomorphic function on ![]() $S$. The
$S$. The ![]() $S$-torsion submodule
$S$-torsion submodule ![]() $\mathcal {M}_\mathrm {t}$ of
$\mathcal {M}_\mathrm {t}$ of ![]() $\mathcal {M}$ is the submodule consisting of
$\mathcal {M}$ is the submodule consisting of ![]() $S$-torsion local sections. Note that if
$S$-torsion local sections. Note that if ![]() $\mathcal {M}$ is a holonomic
$\mathcal {M}$ is a holonomic ![]() $\mathcal {D}_{X\times S/S}$-module, then the
$\mathcal {D}_{X\times S/S}$-module, then the ![]() $\mathcal {D}_{X\times S/S}$-submodule
$\mathcal {D}_{X\times S/S}$-submodule ![]() $\mathcal {M}_\mathrm {t}$ is holonomic because it is an
$\mathcal {M}_\mathrm {t}$ is holonomic because it is an ![]() $\mathcal {O}$-quasi-coherent submodule of
$\mathcal {O}$-quasi-coherent submodule of ![]() $\mathcal {M}$. We say that
$\mathcal {M}$. We say that ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $S$-torsion-free if
$S$-torsion-free if ![]() $\mathcal {M}_\mathrm {t}=0$. We denote by
$\mathcal {M}_\mathrm {t}=0$. We denote by ![]() $\mathcal {M}_{\mathrm {tf}}:\mathcal {M}/\mathcal {M}_\mathrm {t}$ the torsion-free quotient.
$\mathcal {M}_{\mathrm {tf}}:\mathcal {M}/\mathcal {M}_\mathrm {t}$ the torsion-free quotient.
We recall that the duality functor ![]() $\boldsymbol {D}$ for
$\boldsymbol {D}$ for ![]() $\mathcal {D}_{X\times S/S}$-modules was considered in [Reference Monteiro Fernandes and SabbahMFS13, Definition 3.4] and that
$\mathcal {D}_{X\times S/S}$-modules was considered in [Reference Monteiro Fernandes and SabbahMFS13, Definition 3.4] and that ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ is stable under duality which is an involution.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ is stable under duality which is an involution.
2.b Behavior with respect to pullback, pushforward, and external product
(i) For a holomorphic map
 $f:X\rightarrow X'$, we also denote by
$f:X\rightarrow X'$, we also denote by  $f$ the morphism of complex manifolds
$f$ the morphism of complex manifolds  $f\times \operatorname {Id}:X\times S\rightarrow X'\times S$ and by
$f\times \operatorname {Id}:X\times S\rightarrow X'\times S$ and by  ${}_{\scriptscriptstyle \mathrm {D}}f^*$ and
${}_{\scriptscriptstyle \mathrm {D}}f^*$ and  ${}_{\scriptscriptstyle \mathrm {D}}f_*$ the pullback and pushforward functors in the derived category of relative
${}_{\scriptscriptstyle \mathrm {D}}f_*$ the pullback and pushforward functors in the derived category of relative  $\mathcal {D}$-modules.
$\mathcal {D}$-modules.(ii) For a morphism
 $\pi :S\rightarrow S'$ between analytic spaces, we denote by
$\pi :S\rightarrow S'$ between analytic spaces, we denote by  $\pi ^*$ and
$\pi ^*$ and  $R\pi _*$ the natural extension to the category of relative
$R\pi _*$ the natural extension to the category of relative  $\mathcal {D}$-modules of the similar functors defined on the categories of
$\mathcal {D}$-modules of the similar functors defined on the categories of  $\mathcal {O}$-modules
$\mathcal {O}$-modules
Definition 2.10 We say that a ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $f$-(
$f$-( ![]() $\mathcal {O}$-)good (respectively,
$\mathcal {O}$-)good (respectively, ![]() $\pi$-(
$\pi$-( ![]() $\mathcal {O}$-)good) if it is (
$\mathcal {O}$-)good) if it is (![]() $\mathcal {O}$-)good in some neighborhood of each fiber of
$\mathcal {O}$-)good in some neighborhood of each fiber of ![]() $f$ (respectively,
$f$ (respectively, ![]() $\pi$).
$\pi$).
We recall results concerning the behavior with respect to a morphism of complex manifolds.
Proposition 2.11 Let ![]() $\mathcal {M}$ be a coherent
$\mathcal {M}$ be a coherent ![]() $\mathcal {D}_{X\times S/S}$-module.
$\mathcal {D}_{X\times S/S}$-module.
(i) If
 $f:X'\rightarrow X$ is a holomorphic map of complex manifolds, then, for each
$f:X'\rightarrow X$ is a holomorphic map of complex manifolds, then, for each  $\ell \in \mathbb {Z}$,
$\ell \in \mathbb {Z}$,  $\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$ is an
$\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$ is an  $f$-
$f$- $\mathcal {O}$-good
$\mathcal {O}$-good  $\mathcal {D}_{X'\times S/S}$-module.
$\mathcal {D}_{X'\times S/S}$-module.(ii) Let
 $f:X\rightarrow X'$ be a proper holomorphic map. If
$f:X\rightarrow X'$ be a proper holomorphic map. If  $\mathcal {M}$ is
$\mathcal {M}$ is  $f$-good (respectively,
$f$-good (respectively,  $f$-good and holonomic), then, for each
$f$-good and holonomic), then, for each  $\ell$,
$\ell$,  $\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}$ is
$\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}$ is  $\mathcal {D}_{X'\times S/S}$-coherent (respectively, holonomic).
$\mathcal {D}_{X'\times S/S}$-coherent (respectively, holonomic).
Proof. We refer to [Reference Schapira and SchneidersSS94, Theorem 4.2 and Corollary 4.3] for the proof of part (ii) (or one can adapt the proof of [Reference KashiwaraKas03, Theorems 4.25 and 4.27]), whereas for the proof of part (i) we can easily adapt the argument of [Reference Laurent and SchapiraLS87, Proposition 2.1] which gives the absolute case.
Base pullback
Let ![]() $\pi :S'\rightarrow S$ be a morphism of complex analytic manifolds. We also denote by
$\pi :S'\rightarrow S$ be a morphism of complex analytic manifolds. We also denote by ![]() $\pi$ the induced map
$\pi$ the induced map ![]() $\operatorname {Id}\times \pi :X\times S'\to X\times S$. We have
$\operatorname {Id}\times \pi :X\times S'\to X\times S$. We have
hence, ![]() $\mathcal {D}_{X\times S'/S'}$ is a right
$\mathcal {D}_{X\times S'/S'}$ is a right ![]() $\pi ^{-1}\mathcal {D}_{X\times S/S}$-module. One can then define in a natural way the functor
$\pi ^{-1}\mathcal {D}_{X\times S/S}$-module. One can then define in a natural way the functor ![]() $L\pi ^*:\operatorname {\mathsf {D}}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}(\mathcal {D}_{X\times S'/S'})$ as
$L\pi ^*:\operatorname {\mathsf {D}}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}(\mathcal {D}_{X\times S'/S'})$ as ![]() $L\pi ^*(\bullet)=\mathcal {D}_{X\times S'/S'}\otimes ^L_{\pi ^{-1}\mathcal {D}_{X\times S/S}}(\bullet)$.
$L\pi ^*(\bullet)=\mathcal {D}_{X\times S'/S'}\otimes ^L_{\pi ^{-1}\mathcal {D}_{X\times S/S}}(\bullet)$.
The following is straightforward.
Lemma 2.13 Let ![]() $\mathcal {L}$ be an
$\mathcal {L}$ be an ![]() $\mathcal {O}$-quasi-coherent
$\mathcal {O}$-quasi-coherent ![]() $\mathcal {O}_{X\times S}$-module. Then each cohomology sheaf
$\mathcal {O}_{X\times S}$-module. Then each cohomology sheaf ![]() $L^j\pi ^*\mathcal {L}$ is
$L^j\pi ^*\mathcal {L}$ is ![]() $\pi$-
$\pi$-![]() $\mathcal {O}$-good.
$\mathcal {O}$-good.
Lemma 2.14 The functor ![]() $L\pi ^*$ induces a functor
$L\pi ^*$ induces a functor ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S'/S'})$. For a holonomic
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S'/S'})$. For a holonomic ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ and for each
$\mathcal {M}$ and for each ![]() $j$, the characteristic variety
$j$, the characteristic variety ![]() $\operatorname {Char} L^j\pi ^*\mathcal {M}$ is contained in the pullback
$\operatorname {Char} L^j\pi ^*\mathcal {M}$ is contained in the pullback ![]() $\pi ^{-1}\operatorname {Char}\mathcal {M}$ (here,
$\pi ^{-1}\operatorname {Char}\mathcal {M}$ (here, ![]() $\pi$ denotes the map
$\pi$ denotes the map ![]() $T^*X\times S'\rightarrow T^*X\times S$).
$T^*X\times S'\rightarrow T^*X\times S$).
Proof. By using that, locally, a coherent ![]() $\mathcal {D}_{X\times S/S}$-module has a resolution of length
$\mathcal {D}_{X\times S/S}$-module has a resolution of length ![]() $2\dim X$ by free
$2\dim X$ by free ![]() $\mathcal {D}_{X\times S/S}$-modules of finite rank, one obtains the first point for
$\mathcal {D}_{X\times S/S}$-modules of finite rank, one obtains the first point for ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. It thus suffices to prove the second point, which is a local question. One can find such a resolution which is strictly compatible with coherent filtrations relative to
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. It thus suffices to prove the second point, which is a local question. One can find such a resolution which is strictly compatible with coherent filtrations relative to ![]() $F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$. In such a way, one can find that for each
$F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$. In such a way, one can find that for each ![]() $j$,
$j$, ![]() $\operatorname {Char} L^j\pi ^*\mathcal {M}$ is contained in the support of
$\operatorname {Char} L^j\pi ^*\mathcal {M}$ is contained in the support of ![]() $L\pi ^*\mathrm {gr}^F\mathcal {M}$, hence the assertion.
$L\pi ^*\mathrm {gr}^F\mathcal {M}$, hence the assertion.
Base pushforward
We now consider pushforward by a proper morphism ![]() $\pi :S'\rightarrow S$. Owing to (2.12), we have a natural morphism
$\pi :S'\rightarrow S$. Owing to (2.12), we have a natural morphism ![]() $\pi ^{-1}\mathcal {D}_{X\times S/S}\rightarrow \mathcal {D}_{X\times S'/S'}$ which, by adjunction, entails a natural morphism
$\pi ^{-1}\mathcal {D}_{X\times S/S}\rightarrow \mathcal {D}_{X\times S'/S'}$ which, by adjunction, entails a natural morphism ![]() $\mathcal {D}_{X\times S/S}\rightarrow \pi _*\mathcal {D}_{X\times S'/S'}$.
$\mathcal {D}_{X\times S/S}\rightarrow \pi _*\mathcal {D}_{X\times S'/S'}$.
We recall [Reference Monteiro Fernandes and SabbahMFS19, Proposition 1.6].
Proposition 2.15 Assume that ![]() $\pi$ is proper and that
$\pi$ is proper and that ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S'/S'}$-holonomic and
$\mathcal {D}_{X\times S'/S'}$-holonomic and ![]() $\pi$-good. Then, for each
$\pi$-good. Then, for each ![]() $j$,
$j$, ![]() $R^j\pi _*\mathcal {M}$ is
$R^j\pi _*\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S/S}$-holonomic with characteristic variety contained in
$\mathcal {D}_{X\times S/S}$-holonomic with characteristic variety contained in ![]() $\pi (\operatorname {Char}\mathcal {M})$.
$\pi (\operatorname {Char}\mathcal {M})$.
An adjunction formula
Let ![]() $\pi :S'\rightarrow S$ be a morphism of complex manifolds. We make use of the following adjunction formula.
$\pi :S'\rightarrow S$ be a morphism of complex manifolds. We make use of the following adjunction formula.
Lemma 2.16 Let ![]() $\mathcal {M},\mathcal {N}$ be objects of
$\mathcal {M},\mathcal {N}$ be objects of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. Then there is a bi-functorial isomorphism in
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. Then there is a bi-functorial isomorphism in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$:
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$:
If ![]() $\mathcal {N}$ is a coherent
$\mathcal {N}$ is a coherent ![]() $\mathcal {D}_{X\times S/S}$-module, there are functorial morphisms in
$\mathcal {D}_{X\times S/S}$-module, there are functorial morphisms in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$:
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$:
and if ![]() $\pi$ is proper,
$\pi$ is proper, ![]() $R\pi _*L\pi ^*\mathcal {N}\simeq (R\pi _*\mathcal {D}_{X\times S'/S'})\otimes ^L_{\mathcal {D}_{X\times S/S}}\mathcal {N}$ belongs to
$R\pi _*L\pi ^*\mathcal {N}\simeq (R\pi _*\mathcal {D}_{X\times S'/S'})\otimes ^L_{\mathcal {D}_{X\times S/S}}\mathcal {N}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$.
Proof. We have (cf. [Reference KashiwaraKas03, p. 241])
hence (2.16 *) is obtained by adjunction (cf. [Reference Kashiwara and SchapiraKS90, (2.6.15)]). By setting ![]() $\mathcal {M}=\mathcal {N}$ in (2.16 *) we get
$\mathcal {M}=\mathcal {N}$ in (2.16 *) we get ![]() $\operatorname {Hom}_{\mathcal {D}_{X\times S'/S'}}(L\pi ^*\mathcal {N},L\pi ^*\mathcal {N})\simeq \operatorname {Hom}_{\mathcal {D}_{X\times S/S}}(\mathcal {N},R\pi _*L\pi ^*\mathcal {N})$. The image of
$\operatorname {Hom}_{\mathcal {D}_{X\times S'/S'}}(L\pi ^*\mathcal {N},L\pi ^*\mathcal {N})\simeq \operatorname {Hom}_{\mathcal {D}_{X\times S/S}}(\mathcal {N},R\pi _*L\pi ^*\mathcal {N})$. The image of ![]() $\operatorname {Id}$ by this isomorphism is the first morphism in (2.16 **) while the natural morphism
$\operatorname {Id}$ by this isomorphism is the first morphism in (2.16 **) while the natural morphism ![]() $L\pi ^*\mathcal {N}\rightarrow \pi ^*\mathcal {N}$ in
$L\pi ^*\mathcal {N}\rightarrow \pi ^*\mathcal {N}$ in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S'/S'})$ provides the desired morphism
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S'/S'})$ provides the desired morphism ![]() $R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$. The last isomorphism is obtained by the projection formula (cf. [Reference Kashiwara and SchapiraKS90, Proposition 2.6.6]).
$R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$. The last isomorphism is obtained by the projection formula (cf. [Reference Kashiwara and SchapiraKS90, Proposition 2.6.6]).
Remark 2.17 ((External) tensor product)
If ![]() $\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^-(\mathcal {D}_{X\times S/S})$, the tensor product
$\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^-(\mathcal {D}_{X\times S/S})$, the tensor product
is isomorphic to the pullback ![]() ${}_{\scriptscriptstyle \mathrm {D}}\delta ^*(\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N})$ of the
${}_{\scriptscriptstyle \mathrm {D}}\delta ^*(\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N})$ of the ![]() $S$-external tensor product (recall that
$S$-external tensor product (recall that ![]() $\mathcal {D}_{X\times X\times S/S}$ is flat over
$\mathcal {D}_{X\times X\times S/S}$ is flat over ![]() $\mathcal {D}_{X\times S/S}\boxtimes _{\mathcal {O}_S}\mathcal {D}_{X\times S/S}$)
$\mathcal {D}_{X\times S/S}\boxtimes _{\mathcal {O}_S}\mathcal {D}_{X\times S/S}$)
by the diagonal embedding ![]() $\delta :X\times S\mathrel {\hookrightarrow}(X\times X)\times S$ over
$\delta :X\times S\mathrel {\hookrightarrow}(X\times X)\times S$ over ![]() $S$. If
$S$. If ![]() $\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$,
$\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$, ![]() $\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$ belongs to
$\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times X\times S/S})$ and we have
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times X\times S/S})$ and we have
This is seen by considering local resolutions of ![]() $\mathcal {M}$ (respectively,
$\mathcal {M}$ (respectively, ![]() $\mathcal {N}$) by free
$\mathcal {N}$) by free ![]() $\mathcal {D}_{X\times S/S}$-modules, showing both inclusions
$\mathcal {D}_{X\times S/S}$-modules, showing both inclusions ![]() $C\subset T^*X\times \operatorname {Char}(\mathcal {N})$ and
$C\subset T^*X\times \operatorname {Char}(\mathcal {N})$ and ![]() $C\subset \operatorname {Char}(\mathcal {M})\times T^*X$. Therefore, if
$C\subset \operatorname {Char}(\mathcal {M})\times T^*X$. Therefore, if ![]() $\mathcal {M},\mathcal {N}$ are holonomic, so is
$\mathcal {M},\mathcal {N}$ are holonomic, so is ![]() $\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$.
$\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$.
3. Regular holonomic  $\mathcal {D}_{X\times S/S}$-modules
$\mathcal {D}_{X\times S/S}$-modules
In the special case of Lemma 2.14 where ![]() $\pi$ is the inclusion
$\pi$ is the inclusion ![]() $i_{s_o}:\{s_o\}\mathrel {\hookrightarrow} S$ of a point
$i_{s_o}:\{s_o\}\mathrel {\hookrightarrow} S$ of a point ![]() $s_o$ in
$s_o$ in ![]() $S$, we recall a consequence of [Reference KashiwaraKas03, (A.10)].
$S$, we recall a consequence of [Reference KashiwaraKas03, (A.10)].
Proposition 3.1 (Cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 3.1])
For any ![]() $\mathcal {M}, \mathcal {N}$ in
$\mathcal {M}, \mathcal {N}$ in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$, for any
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$, for any ![]() $s_o\in S$, the natural morphism
$s_o\in S$, the natural morphism
is an isomorphism in ![]() $\operatorname {\mathsf {D}}(\mathbb {C}_X)$.
$\operatorname {\mathsf {D}}(\mathbb {C}_X)$.
3.a Characterization of relative regular holonomicity
The category of regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules was introduced in [Reference Monteiro Fernandes and SabbahMFS19] as well as the full subcategory
$\mathcal {D}_{X\times S/S}$-modules was introduced in [Reference Monteiro Fernandes and SabbahMFS19] as well as the full subcategory ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ of
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ of bounded complexes of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ of bounded complexes of ![]() $\mathcal {D}_{X\times S/S}$-modules having regular holonomic cohomology. According to [Reference Monteiro Fernandes and SabbahMFS19], we say that an object
$\mathcal {D}_{X\times S/S}$-modules having regular holonomic cohomology. According to [Reference Monteiro Fernandes and SabbahMFS19], we say that an object ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ is regular if it satisfies:
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ is regular if it satisfies:
![]() $(\mathrm {Reg}\,1)$ For each
$(\mathrm {Reg}\,1)$ For each ![]() $s_o\in S$ and any
$s_o\in S$ and any ![]() $j\in \mathbb {Z}$,
$j\in \mathbb {Z}$, ![]() $Li^*_{s_o}\mathcal {H}^j(\mathcal {M})\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$.
$Li^*_{s_o}\mathcal {H}^j(\mathcal {M})\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$.
An alternative and natural property of regularity would be the following:
![]() $(\mathrm {Reg}\,2)$ For each
$(\mathrm {Reg}\,2)$ For each ![]() $s_o\in S$,
$s_o\in S$, ![]() $Li^*_{s_o}\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$.
$Li^*_{s_o}\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$.
Regularity in either sense is the same property for objects of ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$. Property
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$. Property ![]() $(\mathrm {Reg}\,1)$ is, by definition, compatible with the truncation functors whereas property
$(\mathrm {Reg}\,1)$ is, by definition, compatible with the truncation functors whereas property ![]() $(\mathrm {Reg}\,2)$ is compatible with base change on
$(\mathrm {Reg}\,2)$ is compatible with base change on ![]() $S$, meaning that, for any morphism
$S$, meaning that, for any morphism ![]() $\pi :S'\rightarrow S$ of complex manifolds and any object
$\pi :S'\rightarrow S$ of complex manifolds and any object ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ which satisfies property
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$ which satisfies property ![]() $(\mathrm {Reg}\,2)$, the pullback
$(\mathrm {Reg}\,2)$, the pullback ![]() $L\pi ^\ast (\mathcal {M})\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X'\times S/S})$ satisfies property
$L\pi ^\ast (\mathcal {M})\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X'\times S/S})$ satisfies property ![]() $(\mathrm {Reg}\,2)$ too. We enlarge the setting for further use because both conditions make sense for any complex in
$(\mathrm {Reg}\,2)$ too. We enlarge the setting for further use because both conditions make sense for any complex in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$.
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$.
Proposition 3.2 Let ![]() $Y$ be a hypersurface of
$Y$ be a hypersurface of ![]() $X$. On any complex manifold
$X$. On any complex manifold ![]() $S$:
$S$:
(i) for a complex in
 $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ (respectively, in
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$ (respectively, in  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$), the condition
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$), the condition  $(\mathrm {Reg}\,1)$ is equivalent to
$(\mathrm {Reg}\,1)$ is equivalent to  $(\mathrm {Reg}\,2)$, and we denote both by
$(\mathrm {Reg}\,2)$, and we denote both by  $(\mathrm {Reg})$;
$(\mathrm {Reg})$;(ii) the category of coherent
 $\mathcal {D}_{X\times S/S}$ (respectively, coherent
$\mathcal {D}_{X\times S/S}$ (respectively, coherent  $\mathcal {D}_{X\times S/S}(*Y)$)-modules satisfying
$\mathcal {D}_{X\times S/S}(*Y)$)-modules satisfying  $(\mathrm {Reg})$ is closed under taking extensions in the category
$(\mathrm {Reg})$ is closed under taking extensions in the category  $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$(respectively, in
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$(respectively, in  $\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$) and sub-quotients in the category
$\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$) and sub-quotients in the category  $\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$ (respectively,
$\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$ (respectively,  $\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$);
$\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$);(iii) the category of regular holonomic
 $\mathcal {D}_{X\times S/S}$-modules is closed under taking extensions in
$\mathcal {D}_{X\times S/S}$-modules is closed under taking extensions in  $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ and sub-quotients in
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ and sub-quotients in  $\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$.
$\mathrm {Mod}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$.
We note that statement (iii) follows from statements (i) and (ii) together with Lemma 2.8, so that we focus on the latter properties. The proof in both cases is the same because it is based on the coherence of the rings involved. We provide it in the localized case.
Lemma 3.3 Condition ![]() $(\mathrm {Reg}\,1)$ implies condition
$(\mathrm {Reg}\,1)$ implies condition ![]() $(\mathrm {Reg}\,2)$.
$(\mathrm {Reg}\,2)$.
Proof. We argue by induction on the amplitude of the complex ![]() $\mathcal {M}$. We may assume that
$\mathcal {M}$. We may assume that ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^{\geqslant 0}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ and we consider the following distinguished triangle:
$\mathcal {M}\in \operatorname {\mathsf {D}}^{\geqslant 0}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ and we consider the following distinguished triangle:
where ![]() $\tau ^{\geqslant 1}$ is the truncation functor with respect to the natural
$\tau ^{\geqslant 1}$ is the truncation functor with respect to the natural ![]() $t$-structure on
$t$-structure on ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$. Let us assume that
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$. Let us assume that ![]() $\mathcal {M}$ satisfies
$\mathcal {M}$ satisfies ![]() $(\mathrm {Reg}\,1)$, hence by definition and induction, both
$(\mathrm {Reg}\,1)$, hence by definition and induction, both ![]() $\mathcal {H}^0\mathcal {M}$ and
$\mathcal {H}^0\mathcal {M}$ and ![]() $\tau ^{\geqslant 1}\mathcal {M}$ satisfy
$\tau ^{\geqslant 1}\mathcal {M}$ satisfy ![]() $(\mathrm {Reg}\,1)$. As remarked,
$(\mathrm {Reg}\,1)$. As remarked, ![]() $\mathcal {H}^0\mathcal {M}$ satisfies
$\mathcal {H}^0\mathcal {M}$ satisfies ![]() $(\mathrm {Reg}\,2)$ too and by induction on the amplitude of
$(\mathrm {Reg}\,2)$ too and by induction on the amplitude of ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $\tau ^{\geqslant 1}\mathcal {M}$ satisfies
$\tau ^{\geqslant 1}\mathcal {M}$ satisfies ![]() $(\mathrm {Reg}\,2)$.
$(\mathrm {Reg}\,2)$.
Proof of Proposition 3.2 For ![]() $d\geqslant 0$, we denote by
$d\geqslant 0$, we denote by ![]() $(\mathrm {Reg}\,1)_d$, respectively,
$(\mathrm {Reg}\,1)_d$, respectively, ![]() $(\mathrm {Reg}\,2)_d$, the corresponding condition for
$(\mathrm {Reg}\,2)_d$, the corresponding condition for ![]() $\dim S\leqslant d$. If
$\dim S\leqslant d$. If ![]() $\dim S=0$,
$\dim S=0$, ![]() $(i)_{0}$ holds true, and (ii)
$(i)_{0}$ holds true, and (ii)![]() $_{0}$ is proved, e.g., in [Reference BjörkBjö93, Theorem 5.3.4]. We thus assume from now on that
$_{0}$ is proved, e.g., in [Reference BjörkBjö93, Theorem 5.3.4]. We thus assume from now on that ![]() $d\geqslant 1$ and we proceed by induction on
$d\geqslant 1$ and we proceed by induction on ![]() $d:=\dim S$, denoting by (i)
$d:=\dim S$, denoting by (i)![]() $_{d}$ and (ii)
$_{d}$ and (ii)![]() $_{d}$ the statements of the proposition restricted to
$_{d}$ the statements of the proposition restricted to ![]() $\dim S\leqslant d$. We prove the following implications for
$\dim S\leqslant d$. We prove the following implications for ![]() $d\geqslant 1$:
$d\geqslant 1$:
(a)
 ${\rm (i)}_{d-1} \wedge {\rm (ii)}_{d-1}\Longrightarrow {\rm (i)}_{d}$;
${\rm (i)}_{d-1} \wedge {\rm (ii)}_{d-1}\Longrightarrow {\rm (i)}_{d}$;(b)
 ${\rm (i)}_{d}\wedge {\rm (ii)}_{d-1} \Longrightarrow {\rm (ii)}_{d}$.
${\rm (i)}_{d}\wedge {\rm (ii)}_{d-1} \Longrightarrow {\rm (ii)}_{d}$.
Let us start with implication (a). Assuming that both (i)![]() $_{d-1}$ and (ii)
$_{d-1}$ and (ii)![]() $_{d-1}$ hold, we have to prove that
$_{d-1}$ hold, we have to prove that ![]() $(\mathrm {Reg}\,2)_d\Rightarrow (\mathrm {Reg}\,1)_d$. Owing to the induction hypothesis (i)
$(\mathrm {Reg}\,2)_d\Rightarrow (\mathrm {Reg}\,1)_d$. Owing to the induction hypothesis (i)![]() $_{d-1}$ we simply write
$_{d-1}$ we simply write ![]() $(\mathrm {Reg})_{d-1}$ for either
$(\mathrm {Reg})_{d-1}$ for either ![]() $(\mathrm {Reg}\,1)_{d-1}$ or
$(\mathrm {Reg}\,1)_{d-1}$ or ![]() $(\mathrm {Reg}\,2)_{d-1}$.
$(\mathrm {Reg}\,2)_{d-1}$.
We note that ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ satisfies
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ satisfies ![]() $(\mathrm {Reg}\,2)_d$ if and only if for each smooth codimension-one germ
$(\mathrm {Reg}\,2)_d$ if and only if for each smooth codimension-one germ ![]() $(H,s_o)\subset (S,s_o)$,
$(H,s_o)\subset (S,s_o)$, ![]() $Li_H^*\mathcal {M}$ satisfies
$Li_H^*\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$. It is then enough to prove that, for such an
$(\mathrm {Reg})_{d-1}$. It is then enough to prove that, for such an ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $Li_H^*\mathcal {H}^j\mathcal {M}$ satisfies
$Li_H^*\mathcal {H}^j\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$ for any
$(\mathrm {Reg})_{d-1}$ for any ![]() $j$ and
$j$ and ![]() $H$. We shall argue by induction on the amplitude of
$H$. We shall argue by induction on the amplitude of ![]() $\mathcal {M}$. We may assume that
$\mathcal {M}$. We may assume that ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^{\geqslant 0}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ and we consider the distinguished triangle (3.4). We deduce an isomorphism
$\mathcal {M}\in \operatorname {\mathsf {D}}^{\geqslant 0}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S}(*Y))$ and we consider the distinguished triangle (3.4). We deduce an isomorphism
and an exact sequence
(Note that ![]() $\mathcal {H}^kLi^*_{H}\mathcal {H}^0\mathcal {M}=0$ for
$\mathcal {H}^kLi^*_{H}\mathcal {H}^0\mathcal {M}=0$ for ![]() $k\neq 0, -1$.) As
$k\neq 0, -1$.) As ![]() $L i^*_{H}\mathcal {M}$ satisfies
$L i^*_{H}\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$, so does
$(\mathrm {Reg})_{d-1}$, so does ![]() $\mathcal {H}^k L i^*_{H}\mathcal {M}$ (
$\mathcal {H}^k L i^*_{H}\mathcal {M}$ (![]() $k=-1,0$), and so does
$k=-1,0$), and so does ![]() $\mathcal {H}^{-1}Li^*_{H}\mathcal {H}^0\mathcal {M}$ by (3.5). Since (ii)
$\mathcal {H}^{-1}Li^*_{H}\mathcal {H}^0\mathcal {M}$ by (3.5). Since (ii)![]() $_{d-1}$ is assumed to hold, any coherent sub-quotient of
$_{d-1}$ is assumed to hold, any coherent sub-quotient of ![]() $\mathcal {H}^0 L i^*_{H}\mathcal {M}$ satisfies
$\mathcal {H}^0 L i^*_{H}\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$, hence so does
$(\mathrm {Reg})_{d-1}$, hence so does ![]() $\mathcal {H}^0 L i^*_{H}\mathcal {H}^0\mathcal {M}$, which proves, following Lemma 3.3, that
$\mathcal {H}^0 L i^*_{H}\mathcal {H}^0\mathcal {M}$, which proves, following Lemma 3.3, that ![]() $Li^*_{H}\mathcal {H}^0\mathcal {M}$ satisfies
$Li^*_{H}\mathcal {H}^0\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$. Thus,
$(\mathrm {Reg})_{d-1}$. Thus, ![]() $\mathcal {H}^0\mathcal {M}$ satisfies
$\mathcal {H}^0\mathcal {M}$ satisfies ![]() $(\mathrm {Reg}\,2)_d$ and, by the distinguished triangle (3.4),
$(\mathrm {Reg}\,2)_d$ and, by the distinguished triangle (3.4), ![]() $\tau ^{\geqslant 1}\mathcal {M}$ satisfies
$\tau ^{\geqslant 1}\mathcal {M}$ satisfies ![]() $(\mathrm {Reg}\,2)_d$. Induction on the cohomological length applied to
$(\mathrm {Reg}\,2)_d$. Induction on the cohomological length applied to ![]() $\tau ^{\geqslant 1}\mathcal {M}$ implies that
$\tau ^{\geqslant 1}\mathcal {M}$ implies that ![]() $Li_H^*\mathcal {H}^j\mathcal {M}$ satisfies
$Li_H^*\mathcal {H}^j\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$ for any
$(\mathrm {Reg})_{d-1}$ for any ![]() $j\geqslant 1$, which concludes the proof of implication (a) and we now simply write
$j\geqslant 1$, which concludes the proof of implication (a) and we now simply write ![]() $(\mathrm {Reg})_d$.
$(\mathrm {Reg})_d$.
Let us now prove implication (b). The extension property in (ii)![]() $_d$ is clear. Let us consider stability by sub-quotients in
$_d$ is clear. Let us consider stability by sub-quotients in ![]() $\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$. Let
$\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$. Let ![]() $\mathcal {M}\in \mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$ satisfy
$\mathcal {M}\in \mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$ satisfy ![]() $(\mathrm {Reg})_d$. Given any short exact sequence
$(\mathrm {Reg})_d$. Given any short exact sequence
of coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-modules, we wish to prove that
$\mathcal {D}_{X\times S/S}(*Y)$-modules, we wish to prove that ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ satisfy
$\mathcal {M}_2$ satisfy ![]() $(\mathrm {Reg})_d$. Owing to our assumption on
$(\mathrm {Reg})_d$. Owing to our assumption on ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $Li^*_H\mathcal {M}$ satisfies
$Li^*_H\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$ for any smooth codimension-one germ
$(\mathrm {Reg})_{d-1}$ for any smooth codimension-one germ ![]() $(H,s_o)\subset (S,s_o)$, and it is enough to prove that either
$(H,s_o)\subset (S,s_o)$, and it is enough to prove that either ![]() $Li^*_H\mathcal {M}_1$ or
$Li^*_H\mathcal {M}_1$ or ![]() $Li^*_H\mathcal {M}_2$ satisfies
$Li^*_H\mathcal {M}_2$ satisfies ![]() $(\mathrm {Reg})_{d-1}$. From (3.6) we obtain the long exact sequence:
$(\mathrm {Reg})_{d-1}$. From (3.6) we obtain the long exact sequence:
 \begin{align} 0&\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}_1\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}_2\nonumber\\ &\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_1\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_2\longrightarrow 0. \end{align}
\begin{align} 0&\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}_1\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{-1}Li^*_H\mathcal{M}_2\nonumber\\ &\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_1\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_2\longrightarrow 0. \end{align}
As ![]() $Li^*_H\mathcal {M}$ satisfies
$Li^*_H\mathcal {M}$ satisfies ![]() $(\mathrm {Reg})_{d-1}$, then so do
$(\mathrm {Reg})_{d-1}$, then so do ![]() $\mathcal {H}^{-1}Li^*_H\mathcal {M}_1$ and
$\mathcal {H}^{-1}Li^*_H\mathcal {M}_1$ and ![]() $\mathcal {H}^{0}Li^*_H\mathcal {M}_2$ owing to (ii)
$\mathcal {H}^{0}Li^*_H\mathcal {M}_2$ owing to (ii)![]() $_{d-1}$, and it remains to be proved that either
$_{d-1}$, and it remains to be proved that either ![]() $\mathcal {H}^{-1}Li^*_H\mathcal {M}_2$, or
$\mathcal {H}^{-1}Li^*_H\mathcal {M}_2$, or ![]() $\mathcal {H}^{0}Li^*_H\mathcal {M}_1$, satisfies
$\mathcal {H}^{0}Li^*_H\mathcal {M}_1$, satisfies ![]() $(\mathrm {Reg})_{d-1}$. Let
$(\mathrm {Reg})_{d-1}$. Let ![]() $s$ be a local coordinate on
$s$ be a local coordinate on ![]() $S$ vanishing on
$S$ vanishing on ![]() $H$.
$H$.
Let us denote by ![]() $\mathcal {M}'$ the pullback of
$\mathcal {M}'$ the pullback of ![]() $\mathcal {M}'_2:=\mathrm {tors}_H(\mathcal {M}_2)$ in
$\mathcal {M}'_2:=\mathrm {tors}_H(\mathcal {M}_2)$ in ![]() $\mathcal {M}$ and by
$\mathcal {M}$ and by ![]() $\mathcal {M}_{2,\mathrm {tf}}$ the quotient
$\mathcal {M}_{2,\mathrm {tf}}$ the quotient ![]() $\mathcal {M}_2/\mathcal {M}'_2$. The following commutative diagram is Cartesian and its columns and rows are short exact sequences.
$\mathcal {M}_2/\mathcal {M}'_2$. The following commutative diagram is Cartesian and its columns and rows are short exact sequences.

As ![]() $\mathcal {M}_{2,\mathrm {tf}}$ is
$\mathcal {M}_{2,\mathrm {tf}}$ is ![]() $i^*_{H}$-acyclic, the exact sequence (3.7) for the middle column splits as
$i^*_{H}$-acyclic, the exact sequence (3.7) for the middle column splits as
 \[\begin{gathered} \mathcal{H}^{-1}Li^*_H\mathcal{M}'\stackrel{\sim}{\longrightarrow} \mathcal{H}^{-1}Li^*_H\mathcal{M},\\ 0\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}'\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_{2,\mathrm{tf}}\longrightarrow 0, \end{gathered}\]
\[\begin{gathered} \mathcal{H}^{-1}Li^*_H\mathcal{M}'\stackrel{\sim}{\longrightarrow} \mathcal{H}^{-1}Li^*_H\mathcal{M},\\ 0\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}'\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}\longrightarrow \mathcal{H}^{0}Li^*_H\mathcal{M}_{2,\mathrm{tf}}\longrightarrow 0, \end{gathered}\]
which implies that ![]() $Li_H^*\mathcal {M}'$ and
$Li_H^*\mathcal {M}'$ and ![]() $Li_H^*\mathcal {M}_{2,\mathrm {tf}}$ satisfy
$Li_H^*\mathcal {M}_{2,\mathrm {tf}}$ satisfy ![]() $(\mathrm {Reg})_{d-1}$ by (ii)
$(\mathrm {Reg})_{d-1}$ by (ii)![]() $_{d-1}$, hence
$_{d-1}$, hence ![]() $\mathcal {M}'$ and
$\mathcal {M}'$ and ![]() $\mathcal {M}_{2,\mathrm {tf}}$ satisfy
$\mathcal {M}_{2,\mathrm {tf}}$ satisfy ![]() $(\mathrm {Reg})_{d}$. We now prove that
$(\mathrm {Reg})_{d}$. We now prove that ![]() $Li_H^*\mathcal {M}'_2$ satisfies
$Li_H^*\mathcal {M}'_2$ satisfies ![]() $(\mathrm {Reg})_{d-1}$, which will conclude the proof. As
$(\mathrm {Reg})_{d-1}$, which will conclude the proof. As ![]() $\mathcal {M}'_2$ is
$\mathcal {M}'_2$ is ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent, there exists locally an integer
$\mathcal {D}_{X\times S/S}(*Y)$-coherent, there exists locally an integer ![]() $k\geqslant 1$ such that
$k\geqslant 1$ such that ![]() $s^k\mathcal {M}'_2= 0$. We prove by induction on
$s^k\mathcal {M}'_2= 0$. We prove by induction on ![]() $k$ that any
$k$ that any ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent torsion quotient of a
$\mathcal {D}_{X\times S/S}(*Y)$-coherent torsion quotient of a ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent module satisfying
$\mathcal {D}_{X\times S/S}(*Y)$-coherent module satisfying ![]() $(\mathrm {Reg})_{d}$, satisfies
$(\mathrm {Reg})_{d}$, satisfies ![]() $(\mathrm {Reg})_{d}$ too.
$(\mathrm {Reg})_{d}$ too.
If ![]() $k=1$, we have
$k=1$, we have ![]() $\mathcal {H}^{-1}Li^*_{H}\mathcal {M}'_2\simeq \mathcal {H}^{0}Li^*_{H}\mathcal {M}'_2$, and, by (ii)
$\mathcal {H}^{-1}Li^*_{H}\mathcal {M}'_2\simeq \mathcal {H}^{0}Li^*_{H}\mathcal {M}'_2$, and, by (ii)![]() $_{d-1}$ the latter satisfies
$_{d-1}$ the latter satisfies ![]() $(\mathrm {Reg})_{d-1}$, being a quotient of
$(\mathrm {Reg})_{d-1}$, being a quotient of ![]() $\mathcal {H}^{0}Li^*_{H}\mathcal {M}'$.
$\mathcal {H}^{0}Li^*_{H}\mathcal {M}'$.
If ![]() $k>1$, we argue with the following Cartesian commutative diagram, analogous to (3.8).
$k>1$, we argue with the following Cartesian commutative diagram, analogous to (3.8).

By the induction hypothesis on ![]() $k$,
$k$, ![]() $Li_H^*(s\cdot \mathcal {M}'_2)$ satisfies
$Li_H^*(s\cdot \mathcal {M}'_2)$ satisfies ![]() $(\mathrm {Reg})_{d-1}$ because
$(\mathrm {Reg})_{d-1}$ because ![]() $s\cdot \mathcal {M}'_2$ is a
$s\cdot \mathcal {M}'_2$ is a ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent quotient of
$\mathcal {D}_{X\times S/S}(*Y)$-coherent quotient of ![]() $\mathcal {M}'$ which is annihilated by
$\mathcal {M}'$ which is annihilated by ![]() $s^{k-1}$. It follows that, by considering the middle vertical sequence, so does
$s^{k-1}$. It follows that, by considering the middle vertical sequence, so does ![]() $Li_H^*\mathcal {M}''$. As
$Li_H^*\mathcal {M}''$. As ![]() $\mathcal {M}''_2$ is a
$\mathcal {M}''_2$ is a ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent quotient of
$\mathcal {D}_{X\times S/S}(*Y)$-coherent quotient of ![]() $\mathcal {M}''$ annihilated by
$\mathcal {M}''$ annihilated by ![]() $s$,
$s$, ![]() $Li_H^*(\mathcal {M}''_2)$ satisfies
$Li_H^*(\mathcal {M}''_2)$ satisfies ![]() $(\mathrm {Reg})_{d-1}$. It follows that, by considering the first horizontal sequence, so does
$(\mathrm {Reg})_{d-1}$. It follows that, by considering the first horizontal sequence, so does ![]() $Li_H^*\mathcal {M}_1$, hence, finally, by considering the middle horizontal sequence, so does
$Li_H^*\mathcal {M}_1$, hence, finally, by considering the middle horizontal sequence, so does ![]() $Li_H^*\mathcal {M}'_2$, as required.
$Li_H^*\mathcal {M}'_2$, as required.
Corollary 3.9 The category ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ is a full triangulated subcategory of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ is a full triangulated subcategory of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$ stable by duality.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$ stable by duality.
Proof. We note that ![]() $(\mathrm {Reg}\,2)$ implies that
$(\mathrm {Reg}\,2)$ implies that ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ is a full triangulated subcategory of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ is a full triangulated subcategory of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$. As the latter is a full triangulated subcategory of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S/S})$. As the latter is a full triangulated subcategory of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$, the first assertion follows. Stability by duality follows from the same property in the absolute case (cf., e.g., [Reference BjörkBjö93, Theorem 5.4.15 (4)]), together with the isomorphism
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {coh}}(\mathcal {D}_{X\times S/S})$, the first assertion follows. Stability by duality follows from the same property in the absolute case (cf., e.g., [Reference BjörkBjö93, Theorem 5.4.15 (4)]), together with the isomorphism ![]() $Li^*_{s_o}\boldsymbol {D}\mathcal {M}\simeq \boldsymbol {D} Li^*_{s_o}\mathcal {M}$, which follows from Proposition 3.1.
$Li^*_{s_o}\boldsymbol {D}\mathcal {M}\simeq \boldsymbol {D} Li^*_{s_o}\mathcal {M}$, which follows from Proposition 3.1.
3.b Stability of regular holonomicity under base pullback and base pushforward
For a proper morphism ![]() $f:X\rightarrow Y$, it has been shown in [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.4] that if
$f:X\rightarrow Y$, it has been shown in [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.4] that if ![]() $\mathcal {M}$ is an object of
$\mathcal {M}$ is an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ with
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ with ![]() $f$-good cohomology, then
$f$-good cohomology, then ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}$ belongs to
${}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{Y\times S/S})$. On the other hand, stability of regular holonomicity (and, hence, its coherence) by pullback
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{Y\times S/S})$. On the other hand, stability of regular holonomicity (and, hence, its coherence) by pullback ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*$ has been shown in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] only if
${}_{\scriptscriptstyle \mathrm {D}}f^*$ has been shown in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21] only if ![]() $\dim S=1$ as a consequence of the Riemann–Hilbert correspondence proved there. This will be obtained in general by the proof of Theorem 1 in § 4.e. In this section, we consider on the other hand the behavior with respect to base pullback and pushforward.
$\dim S=1$ as a consequence of the Riemann–Hilbert correspondence proved there. This will be obtained in general by the proof of Theorem 1 in § 4.e. In this section, we consider on the other hand the behavior with respect to base pullback and pushforward.
Proposition 3.10 (Stability under base pullback)
Let ![]() $\pi :S'\rightarrow S$ be a morphism of complex manifolds and let
$\pi :S'\rightarrow S$ be a morphism of complex manifolds and let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$. Then
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$. Then ![]() $L\pi ^*\mathcal {M}$ belongs to
$L\pi ^*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S'/S'})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S'/S'})$.
Proof. We already know that ![]() $L\pi ^*\mathcal {M}$ belongs to
$L\pi ^*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S'/S'})$ by Lemma 2.14. Regularity follows from the isomorphism of functors
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S'/S'})$ by Lemma 2.14. Regularity follows from the isomorphism of functors ![]() $Li_{s'_o}^*L\pi ^*\simeq Li_{\pi (s'_o)}^*$ for any
$Li_{s'_o}^*L\pi ^*\simeq Li_{\pi (s'_o)}^*$ for any ![]() $s'_o\in S'$.
$s'_o\in S'$.
Let ![]() $t_o$ be a fat point of
$t_o$ be a fat point of ![]() $S$, that is, a complex subspace of
$S$, that is, a complex subspace of ![]() $S$ supported on a reduced point
$S$ supported on a reduced point ![]() $|t_o|\in S$. In other words, the ideal
$|t_o|\in S$. In other words, the ideal ![]() $\mathcal {I}_{t_o}\subset \mathcal {O}_S$, which satisfies
$\mathcal {I}_{t_o}\subset \mathcal {O}_S$, which satisfies ![]() $\mathcal {I}_{t_o}\subset \mathfrak {m}_{|t_o|}$ (which is the ideal associated to
$\mathcal {I}_{t_o}\subset \mathfrak {m}_{|t_o|}$ (which is the ideal associated to ![]() $|t_o|$ such that its fiber in
$|t_o|$ such that its fiber in ![]() $|t_o|$ is the maximal ideal of
$|t_o|$ is the maximal ideal of ![]() $\mathcal {O}_{S,|t_o|}$), contains some power
$\mathcal {O}_{S,|t_o|}$), contains some power ![]() $\mathfrak {m}_{|t_o|}^k$. By abuse of notation we still denote by
$\mathfrak {m}_{|t_o|}^k$. By abuse of notation we still denote by ![]() $\mathcal {I}_{t_o}$ (respectively,
$\mathcal {I}_{t_o}$ (respectively, ![]() $\mathfrak {m}_{|t_o|}$) the ideal
$\mathfrak {m}_{|t_o|}$) the ideal ![]() $\mathcal {I}_{t_o,|t_o|}$ (respectively,
$\mathcal {I}_{t_o,|t_o|}$ (respectively, ![]() $\mathfrak {m}_{|t_o|, |t_o|}$) and also the sheaf
$\mathfrak {m}_{|t_o|, |t_o|}$) and also the sheaf ![]() $p^{-1}\mathcal {I}_{t_o}$ (respectively,
$p^{-1}\mathcal {I}_{t_o}$ (respectively, ![]() $p^{-1}\mathfrak {m}_{|t_o|}$). Let
$p^{-1}\mathfrak {m}_{|t_o|}$). Let ![]() $i_{t_o}:t_o\rightarrow S$ denote the natural morphism of complex spaces defined by the surjective morphism
$i_{t_o}:t_o\rightarrow S$ denote the natural morphism of complex spaces defined by the surjective morphism ![]() $\mathcal {O}_S\rightarrow \mathcal {O}_S/\mathcal {I}_{t_o}$. For an
$\mathcal {O}_S\rightarrow \mathcal {O}_S/\mathcal {I}_{t_o}$. For an ![]() $\mathcal {O}_{X\times S}$-module, respectively, a
$\mathcal {O}_{X\times S}$-module, respectively, a ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$, we set
$\mathcal {M}$, we set
that we regard in a natural way as a ![]() $\mathcal {D}_{X}$-module because
$\mathcal {D}_{X}$-module because ![]() $\mathcal {O}_{S,|t_o|}/\mathcal {I}_{t_o}$ is a finite-dimensional vector space. We define thereby the pullback functor
$\mathcal {O}_{S,|t_o|}/\mathcal {I}_{t_o}$ is a finite-dimensional vector space. We define thereby the pullback functor
We note that, endowed with its natural structure of ![]() $\mathcal {D}_{X}$-module,
$\mathcal {D}_{X}$-module, ![]() $i_{t_o}^*\mathcal {D}_{X\times S/S}$ is coherent. As a consequence, if
$i_{t_o}^*\mathcal {D}_{X\times S/S}$ is coherent. As a consequence, if ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent, then
$\mathcal {D}_{X\times S/S}$-coherent, then ![]() $Li_{t_o}^*\mathcal {M}$ has
$Li_{t_o}^*\mathcal {M}$ has ![]() $\mathcal {D}_{X}$-coherent cohomology. In other words,
$\mathcal {D}_{X}$-coherent cohomology. In other words, ![]() $Li_{t_o}^*$ induces a functor
$Li_{t_o}^*$ induces a functor ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X})$.
Corollary 3.11 Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. Then, for any fat point
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S/S})$. Then, for any fat point ![]() $t_o$ of
$t_o$ of ![]() $S$,
$S$, ![]() $Li_{t_o}^*\mathcal {M}$ belongs to
$Li_{t_o}^*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X})$ if and only if
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X})$ if and only if ![]() $Li_{|t_o|}^*\mathcal {M}$ does so.
$Li_{|t_o|}^*\mathcal {M}$ does so.
Proof. For ![]() $k\geqslant 0$, we set
$k\geqslant 0$, we set ![]() $\mathcal {I}_k=\mathcal {I}_{t_o}\cap \mathfrak {m}_{|t_o|}^k$ (with
$\mathcal {I}_k=\mathcal {I}_{t_o}\cap \mathfrak {m}_{|t_o|}^k$ (with ![]() $\mathfrak {m}_{|t_o|}^0:=\mathcal {O}_S$), so that
$\mathfrak {m}_{|t_o|}^0:=\mathcal {O}_S$), so that ![]() $\mathcal {I}_1=\mathcal {I}_{t_o}$ and
$\mathcal {I}_1=\mathcal {I}_{t_o}$ and ![]() $\mathcal {I}_k=\mathfrak {m}_{|t_o|}^k$ for
$\mathcal {I}_k=\mathfrak {m}_{|t_o|}^k$ for ![]() $k$ large enough. It is enough to prove that
$k$ large enough. It is enough to prove that ![]() $p^{-1}(\mathcal {I}_k/\mathcal {I}_{k+1})\otimes ^L_{p^{-1}\mathcal {O}_S}\mathcal {M}$ belongs to
$p^{-1}(\mathcal {I}_k/\mathcal {I}_{k+1})\otimes ^L_{p^{-1}\mathcal {O}_S}\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X})$ for any
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X})$ for any ![]() $k$ if and only if
$k$ if and only if ![]() $Li_{|t_o|}^*\mathcal {M}$ does so. As the sheaf
$Li_{|t_o|}^*\mathcal {M}$ does so. As the sheaf ![]() $\mathcal {I}_k/\mathcal {I}_{k+1}$ is an
$\mathcal {I}_k/\mathcal {I}_{k+1}$ is an ![]() $\mathcal {O}_S/\mathfrak {m}_{|t_o|}$-module supported on
$\mathcal {O}_S/\mathfrak {m}_{|t_o|}$-module supported on ![]() $|t_o|$ whose fiber is a finite-dimensional vector space, we have
$|t_o|$ whose fiber is a finite-dimensional vector space, we have
 \begin{align*} p^{-1}(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes^L_{p^{-1}\mathcal{O}_S}\mathcal{M} &\simeq p^{-1}(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes^L_{p^{-1} (\mathcal{O}_S/\mathfrak{m}_{|t_o|})}(p^{-1}(\mathcal{O}_S/ \mathfrak{m}_{|t_o|})\otimes^L_{p^{-1}\mathcal{O}_S}\mathcal{M})\\ &=(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes Li^*_{|t_o|}\mathcal{M}, \end{align*}
\begin{align*} p^{-1}(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes^L_{p^{-1}\mathcal{O}_S}\mathcal{M} &\simeq p^{-1}(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes^L_{p^{-1} (\mathcal{O}_S/\mathfrak{m}_{|t_o|})}(p^{-1}(\mathcal{O}_S/ \mathfrak{m}_{|t_o|})\otimes^L_{p^{-1}\mathcal{O}_S}\mathcal{M})\\ &=(\mathcal{I}_k/\mathcal{I}_{k+1})\otimes Li^*_{|t_o|}\mathcal{M}, \end{align*}
and the conclusion follows.
Setting 3.12 We consider a local setting where ![]() $S$ is a polydisc
$S$ is a polydisc ![]() $\Delta ^d$ written as
$\Delta ^d$ written as ![]() $\Delta ^{d-1} \times \Delta =S'\times \Delta$, and we denote by
$\Delta ^{d-1} \times \Delta =S'\times \Delta$, and we denote by ![]() $q:S\rightarrow S'$ the projection
$q:S\rightarrow S'$ the projection ![]() $(s',t)\mapsto s'$, and we keep the same notation after taking the product with
$(s',t)\mapsto s'$, and we keep the same notation after taking the product with ![]() $X$. Recall (cf., e.g., [Reference KashiwaraKas03, Proposition A.14]) that the sheaves of rings
$X$. Recall (cf., e.g., [Reference KashiwaraKas03, Proposition A.14]) that the sheaves of rings ![]() $q^{-1}\mathcal {O}_{S'}$,
$q^{-1}\mathcal {O}_{S'}$, ![]() $q^{-1}\mathcal {O}_{X\times S'}$ and
$q^{-1}\mathcal {O}_{X\times S'}$ and ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$ are Noetherian.
$q^{-1}\mathcal {D}_{X\times S'/S'}$ are Noetherian.
Let ![]() $h(s',t)=t^k+\sum _{i=0}^{k-1}h_i(s')t^i$ be a Weierstrass polynomial, with
$h(s',t)=t^k+\sum _{i=0}^{k-1}h_i(s')t^i$ be a Weierstrass polynomial, with ![]() $h_i$ holomorphic on
$h_i$ holomorphic on ![]() $S'$ and let
$S'$ and let ![]() $T=h^{-1}(0)$. The equivalence between the categories of:
$T=h^{-1}(0)$. The equivalence between the categories of:
• coherent
 $\mathcal {O}_S$-modules supported on
$\mathcal {O}_S$-modules supported on  $T$;
$T$;•
 $h$-nilpotent coherent
$h$-nilpotent coherent  $q^{-1}\mathcal {O}_{S'}[t]$-modules;
$q^{-1}\mathcal {O}_{S'}[t]$-modules;•
 $h$-nilpotent
$h$-nilpotent  $q^{-1}\mathcal {O}_{S'}[t]$-modules which are
$q^{-1}\mathcal {O}_{S'}[t]$-modules which are  $q^{-1}\mathcal {O}_{S'}$-coherent;
$q^{-1}\mathcal {O}_{S'}$-coherent;
extends in a natural way to ![]() $\mathcal {O}_{X\times S}$, to
$\mathcal {O}_{X\times S}$, to ![]() $\mathcal {D}_{X\times S/S}$ and to
$\mathcal {D}_{X\times S/S}$ and to ![]() $\mathcal {D}_{X\times S/S}(*Y)$ for a given hypersurface
$\mathcal {D}_{X\times S/S}(*Y)$ for a given hypersurface ![]() $Y$ of
$Y$ of ![]() $X$. For example, in one direction, if
$X$. For example, in one direction, if ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent and supported on
$\mathcal {D}_{X\times S/S}$-coherent and supported on ![]() $X\times T$, then
$X\times T$, then ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-coherent and each local section is annihilated by some power of
$q^{-1}\mathcal {D}_{X\times S'/S'}$-coherent and each local section is annihilated by some power of ![]() $h$. By taking local
$h$. By taking local ![]() $\mathcal {D}_{X\times S/S}$-generators of
$\mathcal {D}_{X\times S/S}$-generators of ![]() $\mathcal {M}$, we conclude that there exists locally an integer
$\mathcal {M}$, we conclude that there exists locally an integer ![]() $\ell \geqslant 1$ such that
$\ell \geqslant 1$ such that ![]() $h^\ell \mathcal {M}=0$. Conversely, if
$h^\ell \mathcal {M}=0$. Conversely, if ![]() $\mathcal {M}$ satisfies the latter property, we can regard it as an
$\mathcal {M}$ satisfies the latter property, we can regard it as an ![]() $h$-nilpotent coherent
$h$-nilpotent coherent ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}[t]$-module and the associated
$q^{-1}\mathcal {D}_{X\times S'/S'}[t]$-module and the associated ![]() $\mathcal {D}_{X\times S/S}$-module is
$\mathcal {D}_{X\times S/S}$-module is ![]() $\mathcal {D}_{X\times S/S}\otimes _{q^{-1}\mathcal {D}_{X\times S'/S'}[t]}\mathcal {M}$.
$\mathcal {D}_{X\times S/S}\otimes _{q^{-1}\mathcal {D}_{X\times S'/S'}[t]}\mathcal {M}$.
By definition, the characteristic variety of a coherent ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-module is (locally) the support in
$q^{-1}\mathcal {D}_{X\times S'/S'}$-module is (locally) the support in ![]() $(T^*X)\times S$ of the graded coherent
$(T^*X)\times S$ of the graded coherent ![]() $q^{-1}\mathrm {gr}^F\mathcal {D}_{X\times S'/S'}$-module with respect to any local coherent
$q^{-1}\mathrm {gr}^F\mathcal {D}_{X\times S'/S'}$-module with respect to any local coherent ![]() $q^{-1}F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S'/S'}$-filtration. Such a module is said to be holonomic if this support is contained in
$q^{-1}F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S'/S'}$-filtration. Such a module is said to be holonomic if this support is contained in ![]() $\Lambda \times S$ for some Lagrangian variety
$\Lambda \times S$ for some Lagrangian variety ![]() $\Lambda \subset T^*X$.
$\Lambda \subset T^*X$.
Remark 3.13 (Holonomic and regular holonomic  $q^{-1}\mathcal {D}_{X\times S'/S'}$-modules)
$q^{-1}\mathcal {D}_{X\times S'/S'}$-modules)
Given a coherent ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ supported on
$\mathcal {M}$ supported on ![]() $T$ as above, one checks that a coherent
$T$ as above, one checks that a coherent ![]() $F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$-filtration is also a coherent
$F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S/S}$-filtration is also a coherent ![]() $q^{-1}F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S'/S'}$-filtration by the above correspondence. As a consequence, such a module is
$q^{-1}F_{\scriptscriptstyle \bullet }\mathcal {D}_{X\times S'/S'}$-filtration by the above correspondence. As a consequence, such a module is ![]() $\mathcal {D}_{X\times S/S}$-holonomic if and only if it is
$\mathcal {D}_{X\times S/S}$-holonomic if and only if it is ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-holonomic.
$q^{-1}\mathcal {D}_{X\times S'/S'}$-holonomic.
On the other hand, we say that a holonomic ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-module
$q^{-1}\mathcal {D}_{X\times S'/S'}$-module ![]() $\mathcal {M}$ is regular if, for any
$\mathcal {M}$ is regular if, for any ![]() $s'_o\in S'$ and any
$s'_o\in S'$ and any ![]() $s_o\in q^{-1}(s'_o)$, the holonomic
$s_o\in q^{-1}(s'_o)$, the holonomic ![]() $\mathcal {D}_{X}$-module
$\mathcal {D}_{X}$-module ![]() $i_{s_o}^{-1}(Li_{q^{-1}(s'_o)}^*\mathcal {M})$ is regular.
$i_{s_o}^{-1}(Li_{q^{-1}(s'_o)}^*\mathcal {M})$ is regular.
Corollary 3.14 A coherent ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}$ supported on
$\mathcal {M}$ supported on ![]() $X\times T$ is regular holonomic if and only if, when regarded as a
$X\times T$ is regular holonomic if and only if, when regarded as a ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-module, it is regular holonomic.
$q^{-1}\mathcal {D}_{X\times S'/S'}$-module, it is regular holonomic.
Proof. By Remark 3.13, we only need to check regularity, and we can suppose from the start that ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mathcal {D}_{X\times S/S}$-holonomic supported on
$\mathcal {D}_{X\times S/S}$-holonomic supported on ![]() $X\times T$. We assume first that
$X\times T$. We assume first that ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-regular. We wish to prove that
$q^{-1}\mathcal {D}_{X\times S'/S'}$-regular. We wish to prove that ![]() $Li_{s_o}^*\mathcal {M}$ is
$Li_{s_o}^*\mathcal {M}$ is ![]() $\mathcal {D}_{X}$-regular holonomic for any
$\mathcal {D}_{X}$-regular holonomic for any ![]() $s_o\in S$. It is enough to prove this for
$s_o\in S$. It is enough to prove this for ![]() $s_o\in T$. Let us choose coordinates
$s_o\in T$. Let us choose coordinates ![]() $(s'_1,\ldots,s'_{d-1},t)$ of
$(s'_1,\ldots,s'_{d-1},t)$ of ![]() $S'\times \Delta$ centered at
$S'\times \Delta$ centered at ![]() $s_o$. There exists
$s_o$. There exists ![]() $k\geqslant 1$ such that
$k\geqslant 1$ such that ![]() $\mathcal {O}_S/(h^k)\otimes ^L_{\mathcal {O}_S}\mathcal {M}\simeq \mathcal {M}[1]\oplus \mathcal {M}$, because
$\mathcal {O}_S/(h^k)\otimes ^L_{\mathcal {O}_S}\mathcal {M}\simeq \mathcal {M}[1]\oplus \mathcal {M}$, because ![]() $h^k\mathcal {M}=0$ for some
$h^k\mathcal {M}=0$ for some ![]() $k\geqslant 1$, so, by the assumption,
$k\geqslant 1$, so, by the assumption,
is a regular holonomic ![]() $\mathcal {D}_{X}$-module. As the support of
$\mathcal {D}_{X}$-module. As the support of ![]() $\mathcal {O}_S/(s'_1,\ldots,s'_{d-1},h^k)$ is a finite union of fat points in
$\mathcal {O}_S/(s'_1,\ldots,s'_{d-1},h^k)$ is a finite union of fat points in ![]() $S$ (defined by the ideal generated by
$S$ (defined by the ideal generated by ![]() $h^k(0,t)$), one of which is supported at
$h^k(0,t)$), one of which is supported at ![]() $s_o$, we conclude that
$s_o$, we conclude that ![]() $Li_{s_o}^*\mathcal {M}$ is a regular holonomic
$Li_{s_o}^*\mathcal {M}$ is a regular holonomic ![]() $\mathcal {D}_{X}$-module by applying Corollary 3.11. The converse is proved similarly.
$\mathcal {D}_{X}$-module by applying Corollary 3.11. The converse is proved similarly.
Theorem 3.15 (Stability under projective base pushforward)
Let ![]() $\pi :S\rightarrow S'$ be a projective morphism of complex manifolds and let
$\pi :S\rightarrow S'$ be a projective morphism of complex manifolds and let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$. Assume that the cohomology of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$. Assume that the cohomology of ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\pi$-good. Then
$\pi$-good. Then ![]() $R\pi _*\mathcal {M}$ belongs to
$R\pi _*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S'/S'})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S'/S'})$.
Proof. A standard consequence of Proposition 2.15 is that ![]() $R\pi _*\mathcal {M}$ belongs to
$R\pi _*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S'/S'})$. Furthermore, we note that the question is local with respect to
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {hol}}(\mathcal {D}_{X\times S'/S'})$. Furthermore, we note that the question is local with respect to ![]() $X$ and to
$X$ and to ![]() $S'$.
$S'$.
Step 1: reduction to the case where ![]() $S'$ is a point. As
$S'$ is a point. As ![]() $\pi$ is projective, we can regard
$\pi$ is projective, we can regard ![]() $\pi$ (locally with respect to
$\pi$ (locally with respect to ![]() $S'$) as the composition of the inclusion
$S'$) as the composition of the inclusion ![]() $S\mathrel {\hookrightarrow}\mathbb {P}^m\times S'$ and the projection
$S\mathrel {\hookrightarrow}\mathbb {P}^m\times S'$ and the projection ![]() ${\mathbb {P}^m\times S'\rightarrow S'}$ for a suitable
${\mathbb {P}^m\times S'\rightarrow S'}$ for a suitable ![]() $m$. Moreover, we note that the result is easy if
$m$. Moreover, we note that the result is easy if ![]() $\pi$ is a closed embedding. We can thus assume that
$\pi$ is a closed embedding. We can thus assume that ![]() $\pi$ is a projection
$\pi$ is a projection ![]() $S=\mathbb {P}^m\times S'\rightarrow S'$. For a complex
$S=\mathbb {P}^m\times S'\rightarrow S'$. For a complex ![]() $\mathcal {M}$ in
$\mathcal {M}$ in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, proving the
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, proving the ![]() $\mathcal {D}_{X\times S'/S'}$-regularity of
$\mathcal {D}_{X\times S'/S'}$-regularity of ![]() $R\pi _*\mathcal {M}$ amounts to proving the
$R\pi _*\mathcal {M}$ amounts to proving the ![]() $\mathcal {D}_{X}$-regularity of
$\mathcal {D}_{X}$-regularity of ![]() $Li_{s'_o}^*R\pi _*\mathcal {M}$ for any
$Li_{s'_o}^*R\pi _*\mathcal {M}$ for any ![]() $s'_o\in S'$. Let
$s'_o\in S'$. Let ![]() $\mathfrak {m}_{s'_o}$ be the maximal ideal sheaf of
$\mathfrak {m}_{s'_o}$ be the maximal ideal sheaf of ![]() $\mathcal {O}_{S'}$ at
$\mathcal {O}_{S'}$ at ![]() $s'_o$. Let us set
$s'_o$. Let us set ![]() $\mathbb {P}^m_{s'_o}=\mathbb {P}^m\times \{s'_o\}$ and consider the following Cartesian square.
$\mathbb {P}^m_{s'_o}=\mathbb {P}^m\times \{s'_o\}$ and consider the following Cartesian square.

Then we have
 \begin{align*} Li_{s'_o}^*R\pi_*\mathcal{M}&=i_{s'_0}^{-1}((\mathcal{O}_{X\times S'}/p^{-1} (\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'})\otimes_{\mathcal{O}_{X\times S'}}^LR\pi_*\mathcal{M})\\ &\simeq i^{-1}_{s'_o}R\pi_* \Big(\pi^{-1}(\mathcal{O}_{X\times S'}/p^{-1}(\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'}) \otimes^L_{\pi^{-1}\mathcal{O}_{X\times S'}}\mathcal{M}\Big)\\ &\simeq R\pi'_*{i'}^{-1}\Big(\pi^{-1}(\mathcal{O}_{X\times S'}/p^{-1} (\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'})\otimes^L_{\pi^{-1}\mathcal{O}_{X\times S'}}\mathcal{M}\Big)\\ &\overset{(*)}{\simeq}R\pi'_*\Big(\mathcal{O}_{X\times \mathbb{P}^m_{s'_o}} \otimes^L_{i'^{-1}\mathcal{O}_{X\times S}}i'^{-1}\mathcal{M}\Big)\\ &=R\pi'_*(Li^{\prime*}\mathcal{M}), \end{align*}
\begin{align*} Li_{s'_o}^*R\pi_*\mathcal{M}&=i_{s'_0}^{-1}((\mathcal{O}_{X\times S'}/p^{-1} (\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'})\otimes_{\mathcal{O}_{X\times S'}}^LR\pi_*\mathcal{M})\\ &\simeq i^{-1}_{s'_o}R\pi_* \Big(\pi^{-1}(\mathcal{O}_{X\times S'}/p^{-1}(\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'}) \otimes^L_{\pi^{-1}\mathcal{O}_{X\times S'}}\mathcal{M}\Big)\\ &\simeq R\pi'_*{i'}^{-1}\Big(\pi^{-1}(\mathcal{O}_{X\times S'}/p^{-1} (\mathfrak{m}_{s'_o})\mathcal{O}_{X\times S'})\otimes^L_{\pi^{-1}\mathcal{O}_{X\times S'}}\mathcal{M}\Big)\\ &\overset{(*)}{\simeq}R\pi'_*\Big(\mathcal{O}_{X\times \mathbb{P}^m_{s'_o}} \otimes^L_{i'^{-1}\mathcal{O}_{X\times S}}i'^{-1}\mathcal{M}\Big)\\ &=R\pi'_*(Li^{\prime*}\mathcal{M}), \end{align*}
where the isomorphism ![]() $(*)$ follows by extension of scalars because
$(*)$ follows by extension of scalars because ![]() $\mathcal {M}$ is a complex of
$\mathcal {M}$ is a complex of ![]() $\mathcal {O}_{X\times S}$-modules. By Proposition 3.10,
$\mathcal {O}_{X\times S}$-modules. By Proposition 3.10, ![]() $Li^{\prime *}\mathcal {M}$ is a complex with regular holonomic cohomologies, so that if we know the theorem for
$Li^{\prime *}\mathcal {M}$ is a complex with regular holonomic cohomologies, so that if we know the theorem for ![]() $\pi '$, we deduce it for
$\pi '$, we deduce it for ![]() $\pi$.
$\pi$.
From now on, we assume that ![]() $S'$ is a point. In such a case,
$S'$ is a point. In such a case, ![]() $S$ is a projective space
$S$ is a projective space ![]() $\mathbb {P}^m$. As the question is local with respect to
$\mathbb {P}^m$. As the question is local with respect to ![]() $X$ and since
$X$ and since ![]() $S$ is compact, we can assume that the sets
$S$ is compact, we can assume that the sets ![]() $I$ and
$I$ and ![]() $J_i$ occurring in (2.6) are finite, so the
$J_i$ occurring in (2.6) are finite, so the ![]() $S$-support
$S$-support ![]() $T$ of
$T$ of ![]() $\mathcal {M}$ is a closed analytic subset of
$\mathcal {M}$ is a closed analytic subset of ![]() $S$. We argue by induction on the dimension of the
$S$. We argue by induction on the dimension of the ![]() $S$-support of
$S$-support of ![]() $\mathcal {M}$.
$\mathcal {M}$.
Step 2: the case ![]() $\dim \operatorname {Supp}_S\mathcal {M}=0$. If the
$\dim \operatorname {Supp}_S\mathcal {M}=0$. If the ![]() $S$-support of
$S$-support of ![]() $\mathcal {M}$ has dimension zero, it consists of a finite number of points, and it is enough to consider the case where the support consists of one point
$\mathcal {M}$ has dimension zero, it consists of a finite number of points, and it is enough to consider the case where the support consists of one point ![]() $s_o\in S$. By a standard argument we may assume that
$s_o\in S$. By a standard argument we may assume that ![]() $\mathcal {M}$ is concentrated in degree zero and locally we can assume that there exists
$\mathcal {M}$ is concentrated in degree zero and locally we can assume that there exists ![]() $k\geqslant 1$ such that, denoting by
$k\geqslant 1$ such that, denoting by ![]() $\mathfrak {m}_{s_o}$ the maximal ideal sheaf of
$\mathfrak {m}_{s_o}$ the maximal ideal sheaf of ![]() $s_o$ in
$s_o$ in ![]() $S$, we have
$S$, we have ![]() $\mathfrak {m}_{s_o}^k\mathcal {M}=0$. If we denote by
$\mathfrak {m}_{s_o}^k\mathcal {M}=0$. If we denote by ![]() $t_o$ the fat point supported by
$t_o$ the fat point supported by ![]() $s_o$ with ring
$s_o$ with ring ![]() $\mathcal {O}_S/\mathfrak {m}_{s_o}^k\mathcal {O}_S$, we conclude that
$\mathcal {O}_S/\mathfrak {m}_{s_o}^k\mathcal {O}_S$, we conclude that ![]() $\mathcal {M}=i_{s_o*}i_{t_o}^*\mathcal {M}$. Therefore,
$\mathcal {M}=i_{s_o*}i_{t_o}^*\mathcal {M}$. Therefore, ![]() $R\pi _*\mathcal {M}= R\pi _*i_{s_o*}i_{t_o}^*\mathcal {M}=i_{t_o}^*\mathcal {M}$. In this case, the theorem follows from Corollary 3.11.
$R\pi _*\mathcal {M}= R\pi _*i_{s_o*}i_{t_o}^*\mathcal {M}=i_{t_o}^*\mathcal {M}$. In this case, the theorem follows from Corollary 3.11.
Step 3: the case ![]() $\dim \operatorname {Supp}_S\mathcal {M}\geqslant 1$. We recall that, in this step,
$\dim \operatorname {Supp}_S\mathcal {M}\geqslant 1$. We recall that, in this step, ![]() $\pi$ is the constant map on
$\pi$ is the constant map on ![]() $S=\mathbb {P}^m$.
$S=\mathbb {P}^m$.
(i) Proof of the regularity of ![]() $\pi _*\mathcal {M}$. Let
$\pi _*\mathcal {M}$. Let ![]() $d\geqslant 1$. We now assume that the statement holds true for any complex
$d\geqslant 1$. We now assume that the statement holds true for any complex ![]() $\mathcal {M}'$ whose
$\mathcal {M}'$ whose ![]() $S$-support has dimension
$S$-support has dimension ![]() $< d$ and we aim at proving the same property for any complex
$< d$ and we aim at proving the same property for any complex ![]() $\mathcal {M}$ with
$\mathcal {M}$ with ![]() $S$-support
$S$-support ![]() $T$ of dimension
$T$ of dimension ![]() $d$. We may then reduce again to the case where
$d$. We may then reduce again to the case where ![]() $\mathcal {M}$ is a single module.
$\mathcal {M}$ is a single module.
We first prove that ![]() $\pi _*\mathcal {M}$ is regular holonomic (instead of all modules
$\pi _*\mathcal {M}$ is regular holonomic (instead of all modules ![]() $R^k\pi _*\mathcal {M}$).
$R^k\pi _*\mathcal {M}$).
One checks that the ![]() $\mathcal {D}_{X\times S/S}$-submodule
$\mathcal {D}_{X\times S/S}$-submodule ![]() $\mathcal {M}'$ of
$\mathcal {M}'$ of ![]() $\mathcal {M}$ consisting of local sections
$\mathcal {M}$ consisting of local sections ![]() $m$ such that the
$m$ such that the ![]() $S$-support of
$S$-support of ![]() $\mathcal {D}_{X\times S/S}\cdot m$ has dimension
$\mathcal {D}_{X\times S/S}\cdot m$ has dimension ![]() $< d$ is holonomic (denoting by
$< d$ is holonomic (denoting by ![]() $T_{< d}$ the union of irreducible components of
$T_{< d}$ the union of irreducible components of ![]() $T$ of dimension
$T$ of dimension ![]() $< d$,
$< d$, ![]() $\mathcal {M}'$ is locally defined as the sheaf of local sections annihilated by some power of the ideal
$\mathcal {M}'$ is locally defined as the sheaf of local sections annihilated by some power of the ideal ![]() $\mathcal {I}_{T_{< d}}$ of
$\mathcal {I}_{T_{< d}}$ of ![]() $T_{< d}$ in
$T_{< d}$ in ![]() $\mathcal {O}_S$). By Proposition 3.2(iii),
$\mathcal {O}_S$). By Proposition 3.2(iii), ![]() $\mathcal {M}'$ is regular holonomic and, by the induction hypothesis,
$\mathcal {M}'$ is regular holonomic and, by the induction hypothesis, ![]() $\pi _*\mathcal {M}'$ is regular holonomic. It is thus enough to prove regularity of
$\pi _*\mathcal {M}'$ is regular holonomic. It is thus enough to prove regularity of ![]() $\pi _*(\mathcal {M}/\mathcal {M}')$, and we can likewise assume that
$\pi _*(\mathcal {M}/\mathcal {M}')$, and we can likewise assume that
(3.16)
 $\mathcal {M}$ has no non-zero coherent submodule with
$\mathcal {M}$ has no non-zero coherent submodule with  $S$-support of dimension
$S$-support of dimension  $< d$.
$< d$.
Let us denote by ![]() $\Lambda$ a Lagrangian subvariety of
$\Lambda$ a Lagrangian subvariety of ![]() $T^*X$ such that the characteristic variety of
$T^*X$ such that the characteristic variety of ![]() $\mathcal {M}$ is contained in
$\mathcal {M}$ is contained in ![]() $\Lambda \times S$. As
$\Lambda \times S$. As ![]() $T$ is compact, it has a finite number of irreducible components and we index by
$T$ is compact, it has a finite number of irreducible components and we index by ![]() $I_d$ those which are of dimension
$I_d$ those which are of dimension ![]() $d$. We choose a point
$d$. We choose a point ![]() $s_i$ on the smooth part of each
$s_i$ on the smooth part of each ![]() $T_i$ (
$T_i$ (![]() $i\in I_d$). For the sake of simplicity, we denote by
$i\in I_d$). For the sake of simplicity, we denote by ![]() $\boldsymbol {s}_o$ the finite set
$\boldsymbol {s}_o$ the finite set ![]() $\{s_i\mid i\in I_d\}$.
$\{s_i\mid i\in I_d\}$.
There is a natural morphism of ![]() $\mathcal {D}_{X}$-modules
$\mathcal {D}_{X}$-modules
which associates to a section ![]() $m\in \Gamma (U;\pi _*\mathcal {M})=\Gamma (U\times S;\mathcal {M})$ (
$m\in \Gamma (U;\pi _*\mathcal {M})=\Gamma (U\times S;\mathcal {M})$ (![]() $U$ open in
$U$ open in ![]() $X$) its germ along
$X$) its germ along ![]() $U\times \boldsymbol {s}_o$. As
$U\times \boldsymbol {s}_o$. As ![]() $\mathcal {M}$ has no
$\mathcal {M}$ has no ![]() $S$-torsion supported in dimension
$S$-torsion supported in dimension ![]() $< d$, this morphism is injective. Indeed, let
$< d$, this morphism is injective. Indeed, let ![]() $x_o\in U\subseteq X$ and let
$x_o\in U\subseteq X$ and let ![]() $m\in \Gamma (U\times S;\mathcal {M})$ belong to the kernel, that is, such that its germ at
$m\in \Gamma (U\times S;\mathcal {M})$ belong to the kernel, that is, such that its germ at ![]() $(x_o,\boldsymbol {s}_o)$ vanishes, i.e.,
$(x_o,\boldsymbol {s}_o)$ vanishes, i.e., ![]() $m$ is zero in some neighborhood of
$m$ is zero in some neighborhood of ![]() $(x_o,\boldsymbol {s}_o)$ that we write
$(x_o,\boldsymbol {s}_o)$ that we write ![]() $U\times V$, up to shrinking
$U\times V$, up to shrinking ![]() $U$. Let us suppose by contradiction that
$U$. Let us suppose by contradiction that ![]() $m\not =0$. Let us consider the coherent
$m\not =0$. Let us consider the coherent ![]() $\mathcal {D}_{U\times S/S}$-submodule
$\mathcal {D}_{U\times S/S}$-submodule ![]() $\mathcal {D}_{U\times S/S}\cdot m\subset \mathcal {M}_{|U\times S}$ which is holonomic with
$\mathcal {D}_{U\times S/S}\cdot m\subset \mathcal {M}_{|U\times S}$ which is holonomic with ![]() $S$-support contained in
$S$-support contained in ![]() $T$. By (3.16)
$T$. By (3.16) ![]() $\mathcal {D}_{U\times S/S}\cdot m$ has
$\mathcal {D}_{U\times S/S}\cdot m$ has ![]() $S$-support of dimension
$S$-support of dimension ![]() $d$. Hence, any irreducible
$d$. Hence, any irreducible ![]() $d$-dimensional component of its
$d$-dimensional component of its ![]() $S$-support is equal to some
$S$-support is equal to some ![]() $T_i$ for a suitable
$T_i$ for a suitable ![]() $i\in I_d$, but because
$i\in I_d$, but because ![]() $m$ is zero on
$m$ is zero on ![]() $U\times V$ this is not possible.
$U\times V$ this is not possible.
Let ![]() $\mathfrak {m}_{\boldsymbol {s}_o}$ denote the ideal sheaf of
$\mathfrak {m}_{\boldsymbol {s}_o}$ denote the ideal sheaf of ![]() $\boldsymbol {s}_o$ in
$\boldsymbol {s}_o$ in ![]() $\mathcal {O}_S$. For each
$\mathcal {O}_S$. For each ![]() $k\geqslant 1$, we consider the induced morphism
$k\geqslant 1$, we consider the induced morphism
The proposition will be proved if we prove that this morphism is injective for ![]() $k$ large enough, because the right-hand side is regular holonomic by Corollary 3.11.
$k$ large enough, because the right-hand side is regular holonomic by Corollary 3.11.
Its kernel ![]() $\mathcal {N}_k$ is a coherent, hence holonomic,
$\mathcal {N}_k$ is a coherent, hence holonomic, ![]() $\mathcal {D}_{X}$-submodule of
$\mathcal {D}_{X}$-submodule of ![]() $\pi _*\mathcal {M}$ and the sequence
$\pi _*\mathcal {M}$ and the sequence ![]() $(\mathcal {N}_k)$ is decreasing with characteristic variety contained in
$(\mathcal {N}_k)$ is decreasing with characteristic variety contained in ![]() $\Lambda$. It is thus stationary. Let
$\Lambda$. It is thus stationary. Let ![]() $\mathcal {N}\subset \pi _*\mathcal {M}$ denote this constant value. We conclude that the map
$\mathcal {N}\subset \pi _*\mathcal {M}$ denote this constant value. We conclude that the map
is zero for any ![]() $k$. As
$k$. As ![]() $\mathcal {N}=\mathcal {N}_k$ for
$\mathcal {N}=\mathcal {N}_k$ for ![]() $k$ large enough, we aim at proving that
$k$ large enough, we aim at proving that ![]() $\mathcal {N}=0$.
$\mathcal {N}=0$.
The image of ![]() $\mathcal {N}$ by (3.17) is contained in
$\mathcal {N}$ by (3.17) is contained in ![]() $\mathop {\textstyle \bigcap } _ki_{\boldsymbol {s}_o}^{-1}\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}$, and because (3.17) is injective, it suffices to prove that
$\mathop {\textstyle \bigcap } _ki_{\boldsymbol {s}_o}^{-1}\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}$, and because (3.17) is injective, it suffices to prove that ![]() $\mathcal {M}':=\mathop {\textstyle \bigcap } _ki_{\boldsymbol {s}_o}^{-1}\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}=0$. For
$\mathcal {M}':=\mathop {\textstyle \bigcap } _ki_{\boldsymbol {s}_o}^{-1}\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}=0$. For ![]() $x_o\in X$, let us denote by
$x_o\in X$, let us denote by ![]() $\mathcal {D}_{(x_o,\boldsymbol {s}_o)}$ the germ at
$\mathcal {D}_{(x_o,\boldsymbol {s}_o)}$ the germ at ![]() $(x_o,\boldsymbol {s}_o)$ of
$(x_o,\boldsymbol {s}_o)$ of ![]() $\mathcal {D}_{X\times S/S}$ and similarly by
$\mathcal {D}_{X\times S/S}$ and similarly by ![]() $\mathcal {M}_{(x_o,\boldsymbol {s}_o)}$ that of
$\mathcal {M}_{(x_o,\boldsymbol {s}_o)}$ that of ![]() $\mathcal {M}$. It thus suffices to prove that, for all
$\mathcal {M}$. It thus suffices to prove that, for all ![]() $x_o\in X$, the germ
$x_o\in X$, the germ ![]() $\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=\mathop {\textstyle \bigcap } _k\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}_{(x_o,\boldsymbol {s}_o)}$ is zero. We note that
$\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=\mathop {\textstyle \bigcap } _k\mathfrak {m}_{\boldsymbol {s}_o}^k\mathcal {M}_{(x_o,\boldsymbol {s}_o)}$ is zero. We note that ![]() $\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$ is of finite type over
$\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$ is of finite type over ![]() $\mathcal {D}_{(x_o,\boldsymbol {s}_o)}$ because the latter ring is Noetherian, hence
$\mathcal {D}_{(x_o,\boldsymbol {s}_o)}$ because the latter ring is Noetherian, hence ![]() $\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$ is holonomic with characteristic variety contained in
$\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$ is holonomic with characteristic variety contained in ![]() $\Lambda _{x_o}\times (S,\boldsymbol {s}_o)$, where
$\Lambda _{x_o}\times (S,\boldsymbol {s}_o)$, where ![]() $\Lambda _{x_o}$ is the germ of
$\Lambda _{x_o}$ is the germ of ![]() $\Lambda$ along
$\Lambda$ along ![]() $T^*_{x_o}X$. Furthermore, it satisfies
$T^*_{x_o}X$. Furthermore, it satisfies ![]() $\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=\mathfrak {m}_{\boldsymbol {s}_o}\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$. The Nakayama-type argument given in the proof of [Reference Monteiro Fernandes and SabbahMFS19, Proposition 1.9(1)] shows that
$\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=\mathfrak {m}_{\boldsymbol {s}_o}\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}$. The Nakayama-type argument given in the proof of [Reference Monteiro Fernandes and SabbahMFS19, Proposition 1.9(1)] shows that ![]() $\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=0$ for each
$\mathcal {M}'_{(x_o,\boldsymbol {s}_o)}=0$ for each ![]() $x_o$. This concludes the proof of step 3(i).
$x_o$. This concludes the proof of step 3(i).
(ii) Regularity of ![]() $R^k\pi _*\mathcal {M}$. We use the result of step 3(i) in order to prove holonomicity and regularity of
$R^k\pi _*\mathcal {M}$. We use the result of step 3(i) in order to prove holonomicity and regularity of ![]() $R^k\pi _*\mathcal {M}$ for all
$R^k\pi _*\mathcal {M}$ for all ![]() $k$.
$k$.
For any ![]() $\ell \in \mathbb {Z}$, we consider the line bundle
$\ell \in \mathbb {Z}$, we consider the line bundle ![]() $\mathcal {O}_S(\ell )$ that we can realize as
$\mathcal {O}_S(\ell )$ that we can realize as ![]() $\mathcal {O}_S(\ell H)$ for any hyperplane
$\mathcal {O}_S(\ell H)$ for any hyperplane ![]() $H$ of
$H$ of ![]() $S$. For a
$S$. For a ![]() $\mathcal {D}_{X\times S/S}$-module or an
$\mathcal {D}_{X\times S/S}$-module or an ![]() $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module ![]() $\mathcal {N}$, we set
$\mathcal {N}$, we set ![]() $\mathcal {N}(\ell )=p^{-1}\mathcal {O}_S(\ell )\otimes _{p^{-1}\mathcal {O}_S} \mathcal {N}$.
$\mathcal {N}(\ell )=p^{-1}\mathcal {O}_S(\ell )\otimes _{p^{-1}\mathcal {O}_S} \mathcal {N}$.
We apply the technical Lemma 3.18 below to ![]() $\mathcal {M}$. We note that
$\mathcal {M}$. We note that ![]() $\mathcal {M}(\ell )$ is
$\mathcal {M}(\ell )$ is ![]() $\mathcal {D}_{X\times S/S}$ regular holonomic: indeed, this is a local property on
$\mathcal {D}_{X\times S/S}$ regular holonomic: indeed, this is a local property on ![]() $S$, and locally
$S$, and locally ![]() $\mathcal {O}_S(\ell )\simeq \mathcal {O}_S$. In addition,
$\mathcal {O}_S(\ell )\simeq \mathcal {O}_S$. In addition, ![]() $\mathcal {M}(\ell )$ is
$\mathcal {M}(\ell )$ is ![]() $\pi$-good. Furthermore, we choose a hyperplane
$\pi$-good. Furthermore, we choose a hyperplane ![]() $H\subset S$ such that
$H\subset S$ such that ![]() $\dim H\cap T<\dim T$, and we realize
$\dim H\cap T<\dim T$, and we realize ![]() $\mathcal {O}_S(\ell )$ as
$\mathcal {O}_S(\ell )$ as ![]() $\mathcal {O}_S(\ell H)$. We also consider
$\mathcal {O}_S(\ell H)$. We also consider ![]() $\mathcal {M}(\ell H)$ with such a choice of
$\mathcal {M}(\ell H)$ with such a choice of ![]() $H$. From step 3(i), we know that
$H$. From step 3(i), we know that ![]() $\pi _*\mathcal {M}(\ell H)$ is
$\pi _*\mathcal {M}(\ell H)$ is ![]() $\mathcal {D}_{X}$-regular. Let us consider the sheaf
$\mathcal {D}_{X}$-regular. Let us consider the sheaf ![]() $\mathcal {O}_{\ell H}$ defined by the exact sequence
$\mathcal {O}_{\ell H}$ defined by the exact sequence
yielding to the distinguished triangle
where ![]() $\mathcal {N}$ is a complex in
$\mathcal {N}$ is a complex in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ with
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ with ![]() $S$-support contained in
$S$-support contained in ![]() $T\cap H$. We deduce the long exact sequence
$T\cap H$. We deduce the long exact sequence
and the isomorphisms ![]() $R^{k+1}\pi _*\mathcal {M}\simeq H^kR\pi _*\mathcal {N}$ for
$R^{k+1}\pi _*\mathcal {M}\simeq H^kR\pi _*\mathcal {N}$ for ![]() $k\geqslant 1$. By the induction hypothesis,
$k\geqslant 1$. By the induction hypothesis, ![]() $R\pi _*\mathcal {N}$ belongs to
$R\pi _*\mathcal {N}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$. The latter isomorphism implies the regularity of
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$. The latter isomorphism implies the regularity of ![]() $R^{k+1}\pi _*\mathcal {M}$ for
$R^{k+1}\pi _*\mathcal {M}$ for ![]() $k\geqslant 1$, and, together with Corollary 3.9, it implies that of
$k\geqslant 1$, and, together with Corollary 3.9, it implies that of ![]() $\pi _*\mathcal {M}$ and
$\pi _*\mathcal {M}$ and ![]() $R^1\pi _*\mathcal {M}$.
$R^1\pi _*\mathcal {M}$.
Lemma 3.18 Let us assume ![]() $S=\mathbb {P}^ m$. Let
$S=\mathbb {P}^ m$. Let ![]() $\mathcal {N}$ be a coherent
$\mathcal {N}$ be a coherent ![]() $\pi$-good
$\pi$-good ![]() $\mathcal {D}_{X\times S/S}$-module. Then, for any
$\mathcal {D}_{X\times S/S}$-module. Then, for any ![]() $x_o\in X$, there exists a neighborhood
$x_o\in X$, there exists a neighborhood ![]() $\mathrm {nb}(x_o)\subset X$ and an integer
$\mathrm {nb}(x_o)\subset X$ and an integer ![]() $\ell \geqslant 0$ such that, for any
$\ell \geqslant 0$ such that, for any ![]() $k\geqslant 1$,
$k\geqslant 1$, ![]() $R^k\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}=0$.
$R^k\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}=0$.
A similar result is well-known to hold for a coherent ![]() $\mathcal {O}_{X\times S}$-module, as a consequence of Grauert–Remmert's Theorems A and B (cf. [Reference Grauert and RemmertGR58] and [Reference Bănică and StănăşilăBS76, Theorem IV.2.1]).
$\mathcal {O}_{X\times S}$-module, as a consequence of Grauert–Remmert's Theorems A and B (cf. [Reference Grauert and RemmertGR58] and [Reference Bănică and StănăşilăBS76, Theorem IV.2.1]).
Proof. For any ![]() $N\geqslant 1$, by iteration of Lemma 2.4(iii) we obtain a distinguished triangle on
$N\geqslant 1$, by iteration of Lemma 2.4(iii) we obtain a distinguished triangle on ![]() $\mathrm {nb}(x_o)\times S$:
$\mathrm {nb}(x_o)\times S$:
Let us choose ![]() $N=2m+1$ and let
$N=2m+1$ and let ![]() $\ell$ be an integer given by Grauert–Remmert's theorems for
$\ell$ be an integer given by Grauert–Remmert's theorems for ![]() $\mathcal {L}_i$ (
$\mathcal {L}_i$ (![]() $i=-N,\ldots,0$) in
$i=-N,\ldots,0$) in ![]() $\mathrm {nb}(x_o)$. We consider the same triangle obtained after tensoring with
$\mathrm {nb}(x_o)$. We consider the same triangle obtained after tensoring with ![]() $p^{-1}\mathcal {O}_S(\ell )$. As
$p^{-1}\mathcal {O}_S(\ell )$. As ![]() $\pi$ has cohomological dimension
$\pi$ has cohomological dimension ![]() $2m$, we find that
$2m$, we find that ![]() $R^k\pi _*\mathcal {N}'(\ell )[N]=0$ for any
$R^k\pi _*\mathcal {N}'(\ell )[N]=0$ for any ![]() $k\geqslant 0$. On the other hand, on
$k\geqslant 0$. On the other hand, on ![]() $\mathrm {nb}(x_o)$ (cf. (2.1)),
$\mathrm {nb}(x_o)$ (cf. (2.1)),
 \begin{align*} R\pi_*(\mathcal{D}_{X\times S/S}\otimes_{\mathcal{O}_{X\times S}}\mathcal{L}_i(\ell))&\simeq R\pi_*(\pi^{-1}\mathcal{D}_{X}\otimes_{\pi^{-1}\mathcal{O}_X}\mathcal{L}_i(\ell))\\ &\simeq\mathcal{D}_{X}\otimes_{\mathcal{O}_X}R\pi_*\mathcal{L}_i(\ell)=\mathcal{D}_{X}\otimes_{\mathcal{O}_X}\pi_*\mathcal{L}_i(\ell). \end{align*}
\begin{align*} R\pi_*(\mathcal{D}_{X\times S/S}\otimes_{\mathcal{O}_{X\times S}}\mathcal{L}_i(\ell))&\simeq R\pi_*(\pi^{-1}\mathcal{D}_{X}\otimes_{\pi^{-1}\mathcal{O}_X}\mathcal{L}_i(\ell))\\ &\simeq\mathcal{D}_{X}\otimes_{\mathcal{O}_X}R\pi_*\mathcal{L}_i(\ell)=\mathcal{D}_{X}\otimes_{\mathcal{O}_X}\pi_*\mathcal{L}_i(\ell). \end{align*}
As ![]() $R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$ is in non-negative degrees, it follows that
$R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$ is in non-negative degrees, it follows that ![]() $R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$ is isomorphic to the complex
$R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$ is isomorphic to the complex ![]() $\tau ^{\geqslant 0}(\mathcal {D}_{X}\otimes _{\mathcal {O}_X}\pi _*\mathcal {L}_{\scriptscriptstyle \bullet }(\ell ))$ and because the latter is in non-positive degrees, we conclude that
$\tau ^{\geqslant 0}(\mathcal {D}_{X}\otimes _{\mathcal {O}_X}\pi _*\mathcal {L}_{\scriptscriptstyle \bullet }(\ell ))$ and because the latter is in non-positive degrees, we conclude that ![]() $R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}\simeq \pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$.
$R\pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}\simeq \pi _*\mathcal {N}(\ell )_{|\mathrm {nb}(x_o)}$.
3.c Integrable regular holonomic  $\mathcal {D}_{X\times S/S}$-modules
$\mathcal {D}_{X\times S/S}$-modules
The following proposition, answering a question of Lei Wu, shows that, under a suitable condition on the characteristic variety, a coherent ![]() $\mathcal {D}_{X\times S/S}$-submodule of a regular holonomic
$\mathcal {D}_{X\times S/S}$-submodule of a regular holonomic ![]() $\mathcal {D}_{X\times S}$-module is relatively regular holonomic. We call such
$\mathcal {D}_{X\times S}$-module is relatively regular holonomic. We call such ![]() $\mathcal {D}_{X\times S/S}$-modules integrable because their relative connection can be lifted as an integrable connection, i.e., a
$\mathcal {D}_{X\times S/S}$-modules integrable because their relative connection can be lifted as an integrable connection, i.e., a ![]() $\mathcal {D}_{X\times S}$-module structure.The condition on the characteristic variety is due to the restrictive definition of a holonomic
$\mathcal {D}_{X\times S}$-module structure.The condition on the characteristic variety is due to the restrictive definition of a holonomic ![]() $\mathcal {D}_{X\times S/S}$-module (cf. after Lemma 2.4).
$\mathcal {D}_{X\times S/S}$-module (cf. after Lemma 2.4).
Proposition 3.19 Let ![]() $X$ and
$X$ and ![]() $S$ be complex manifolds and let
$S$ be complex manifolds and let ![]() $\mathcal {N}$ be a regular holonomic
$\mathcal {N}$ be a regular holonomic ![]() $\mathcal {D}_{X\times S}$-module. Assume that the characteristic variety of
$\mathcal {D}_{X\times S}$-module. Assume that the characteristic variety of ![]() $\mathcal {N}$ is contained in
$\mathcal {N}$ is contained in ![]() $\Lambda \times T^*S$ for some conic Lagrangian closed analytic subset
$\Lambda \times T^*S$ for some conic Lagrangian closed analytic subset ![]() $\Lambda$ in
$\Lambda$ in ![]() $T^*X$. Let
$T^*X$. Let ![]() $\mathcal {M}$ be a coherent
$\mathcal {M}$ be a coherent ![]() $\mathcal {D}_{X\times S/S}$-submodule of
$\mathcal {D}_{X\times S/S}$-submodule of ![]() $\mathcal {N}$. Then
$\mathcal {N}$. Then ![]() $\mathcal {M}$ is a regular holonomic
$\mathcal {M}$ is a regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-module.
$\mathcal {D}_{X\times S/S}$-module.
Let us first recall two properties (see (3.20) and (3.21)) of regular holonomic ![]() $\mathcal {D}_{X\times S}$-modules that will be useful for the proof and do not depend on the assumption on
$\mathcal {D}_{X\times S}$-modules that will be useful for the proof and do not depend on the assumption on ![]() $\operatorname {Char}\mathcal {N}$ made in the proposition.
$\operatorname {Char}\mathcal {N}$ made in the proposition.
Let ![]() $\mathcal {N}$ be any regular holonomic
$\mathcal {N}$ be any regular holonomic ![]() $\mathcal {D}_{X\times S}$-module and let
$\mathcal {D}_{X\times S}$-module and let ![]() $\mathcal {M}$ be a coherent
$\mathcal {M}$ be a coherent ![]() $\mathcal {D}_{X\times S/S}$-submodule of
$\mathcal {D}_{X\times S/S}$-submodule of ![]() $\mathcal {N}$. Any irreducible component of
$\mathcal {N}$. Any irreducible component of ![]() $\operatorname {Char}\mathcal {N}$ projects to
$\operatorname {Char}\mathcal {N}$ projects to ![]() $X\times S$ as an irreducible closed analytic subset
$X\times S$ as an irreducible closed analytic subset ![]() $Z$ and, denoting by
$Z$ and, denoting by ![]() $Z^\circ$ the smooth part of
$Z^\circ$ the smooth part of ![]() $Z$, this irreducible component is the closure of the conormal bundle
$Z$, this irreducible component is the closure of the conormal bundle ![]() $T^*_{Z^\circ }(X\times S)$, that we denote by
$T^*_{Z^\circ }(X\times S)$, that we denote by ![]() $T^*_Z(X\times S)$. We also denote by
$T^*_Z(X\times S)$. We also denote by ![]() $Z^{\circ \circ }$ the open set of the smooth locus
$Z^{\circ \circ }$ the open set of the smooth locus ![]() $Z^\circ$ on which
$Z^\circ$ on which ![]() $p_{Z^\circ }:Z^\circ \rightarrow S$ has maximal rank. The closure in the relative cotangent space
$p_{Z^\circ }:Z^\circ \rightarrow S$ has maximal rank. The closure in the relative cotangent space ![]() $T^*(X\times S/S)$ of the relative conormal bundle
$T^*(X\times S/S)$ of the relative conormal bundle ![]() $T^*_{p|Z^{\circ \circ }}(X\times S/S)$ is denoted by
$T^*_{p|Z^{\circ \circ }}(X\times S/S)$ is denoted by ![]() $T^*_{p|Z}(X\times S/S)$, and is a conic analytic subset of
$T^*_{p|Z}(X\times S/S)$, and is a conic analytic subset of ![]() $T^*(X\times S/S)$.
$T^*(X\times S/S)$.
(3.20) According to [Reference SabbahSab87, Theorem 3.2] any irreducible component of
 $\operatorname {Char}\mathcal {M}$ is equal to
$\operatorname {Char}\mathcal {M}$ is equal to  $T^*_{p|Z}(X\times S/S)$ for some
$T^*_{p|Z}(X\times S/S)$ for some  $Z$ such that
$Z$ such that  $T^*_Z(X\times S)$ is an irreducible component of
$T^*_Z(X\times S)$ is an irreducible component of  $\operatorname {Char}\mathcal {N}$.
$\operatorname {Char}\mathcal {N}$.
Assume furthermore that ![]() $\dim S=1$. For each
$\dim S=1$. For each ![]() $s_o\in S$, we denote by
$s_o\in S$, we denote by ![]() $s$ a local coordinate on
$s$ a local coordinate on ![]() $S$ vanishing at
$S$ vanishing at ![]() $s_o$. We postpone after the proof of Proposition 3.19 that of the following classical result.
$s_o$. We postpone after the proof of Proposition 3.19 that of the following classical result.
(3.21) Under the above assumptions, the kernel and cokernel of
 $s:\mathcal {M}\rightarrow \mathcal {M}$ are regular holonomic
$s:\mathcal {M}\rightarrow \mathcal {M}$ are regular holonomic  $\mathcal {D}_{X}$-modules.
$\mathcal {D}_{X}$-modules.
Proof of Proposition 3.19, step 1 We now add the assumption on ![]() $\operatorname {Char}\mathcal {N}$. We first show that
$\operatorname {Char}\mathcal {N}$. We first show that ![]() $\mathcal {M}$ is relative holonomic with characteristic variety contained in
$\mathcal {M}$ is relative holonomic with characteristic variety contained in ![]() $\Lambda \times S$. We note that
$\Lambda \times S$. We note that ![]() $T^*_Z(X\times S)$ is contained in
$T^*_Z(X\times S)$ is contained in ![]() $\Lambda \times T^*S$ if and only if
$\Lambda \times T^*S$ if and only if ![]() $Z$ decomposes as the product
$Z$ decomposes as the product ![]() $Y\times T$ for some irreducible closed analytic subsets
$Y\times T$ for some irreducible closed analytic subsets ![]() $Y\subset X$ and
$Y\subset X$ and ![]() $T\subset S$ and
$T\subset S$ and ![]() $T^*_YX$ is an irreducible component of
$T^*_YX$ is an irreducible component of ![]() $\Lambda$ (this seen by considering first the smooth part
$\Lambda$ (this seen by considering first the smooth part ![]() $Z^\circ$). It is then easily seen that
$Z^\circ$). It is then easily seen that ![]() $T^*_{p|Z}(X\times S/S)=(T^*_YX)\times T,$ hence is contained in
$T^*_{p|Z}(X\times S/S)=(T^*_YX)\times T,$ hence is contained in ![]() $\Lambda \times S$. The conclusion follows from (3.20).
$\Lambda \times S$. The conclusion follows from (3.20).
Proof of Proposition 3.19, step 2 It remains to show the relative regularity of ![]() $\mathcal {M}$. We argue by induction on
$\mathcal {M}$. We argue by induction on ![]() $d=\dim S$. If
$d=\dim S$. If ![]() $d=1$, relative regularity is provided by (3.21), because we already have relative holonomicity by step 1. We thus assume that the statement of the proposition holds whenever
$d=1$, relative regularity is provided by (3.21), because we already have relative holonomicity by step 1. We thus assume that the statement of the proposition holds whenever ![]() $\dim S\leqslant d-1$ and we assume
$\dim S\leqslant d-1$ and we assume ![]() $\dim S=d\geqslant 2$. The question being local, we fix a local coordinate
$\dim S=d\geqslant 2$. The question being local, we fix a local coordinate ![]() $s$ in
$s$ in ![]() $S$, defining a smooth hypersurface
$S$, defining a smooth hypersurface ![]() $H:=\{s=0\}$. Locally, we can assume that
$H:=\{s=0\}$. Locally, we can assume that ![]() $S=H\times \mathbb {C}$. According to Proposition 3.2, we are reduced to proving the following.
$S=H\times \mathbb {C}$. According to Proposition 3.2, we are reduced to proving the following.
(3.22) The kernel and cokernel of
 $s\colon \mathcal {M} \rightarrow \mathcal {M}$ are regular holonomic
$s\colon \mathcal {M} \rightarrow \mathcal {M}$ are regular holonomic  $\mathcal {D}_{X\times H/H}$-modules.
$\mathcal {D}_{X\times H/H}$-modules.
For the sake of clarity we set
We denote by ![]() $\mathcal {M}_1$ the
$\mathcal {M}_1$ the ![]() $\mathcal {D}_{X'\times S'/S'}$-submodule of the regular holonomic
$\mathcal {D}_{X'\times S'/S'}$-submodule of the regular holonomic ![]() $\mathcal {D}_{X'\times S'}$-module
$\mathcal {D}_{X'\times S'}$-module ![]() $\mathcal {N}$ generated by
$\mathcal {N}$ generated by ![]() $\mathcal {M}$. It is
$\mathcal {M}$. It is ![]() $\mathcal {D}_{X'\times S'/S'}$–coherent, so by (3.21), the kernel
$\mathcal {D}_{X'\times S'/S'}$–coherent, so by (3.21), the kernel ![]() $\mathcal {N}_1$ and the cokernel
$\mathcal {N}_1$ and the cokernel ![]() $\mathcal {N}'_1$ of
$\mathcal {N}'_1$ of ![]() $s:\mathcal {M}_1\rightarrow \mathcal {M}_1$ are
$s:\mathcal {M}_1\rightarrow \mathcal {M}_1$ are ![]() $\mathcal {D}_{X'}$-regular holonomic.
$\mathcal {D}_{X'}$-regular holonomic.
Claim The characteristic varieties ![]() $\operatorname {Char}\mathcal {N}_1$ and
$\operatorname {Char}\mathcal {N}_1$ and ![]() $\operatorname {Char}\mathcal {N}'_1$ are contained in
$\operatorname {Char}\mathcal {N}'_1$ are contained in ![]() $\Lambda \times T^*H$.
$\Lambda \times T^*H$.
Proof. We apply (3.20) to ![]() $\mathcal {M}_1 \subset \mathcal {N}$ and to the map
$\mathcal {M}_1 \subset \mathcal {N}$ and to the map ![]() $X'\times S' \rightarrow S'$. As any irreducible component of
$X'\times S' \rightarrow S'$. As any irreducible component of ![]() $\operatorname {Char}\mathcal {N}$ takes the form
$\operatorname {Char}\mathcal {N}$ takes the form ![]() $T^*_YX\times T^*_TS=T^*_Z(X'\times S')$ with
$T^*_YX\times T^*_TS=T^*_Z(X'\times S')$ with ![]() $Z=Y\times T$, any irreducible component of
$Z=Y\times T$, any irreducible component of ![]() $\operatorname {Char}\mathcal {M}_1$ takes the form
$\operatorname {Char}\mathcal {M}_1$ takes the form ![]() $T^*_{p'_{|Z}}(X'\times S'/S')$ for some such
$T^*_{p'_{|Z}}(X'\times S'/S')$ for some such ![]() $Z$. Denoting by
$Z$. Denoting by ![]() $q:S\rightarrow S'$ the projection
$q:S\rightarrow S'$ the projection ![]() $H\times S'\rightarrow S'$, the latter space reads
$H\times S'\rightarrow S'$, the latter space reads
The fiber of the composition ![]() $T^*_{q|T}(H\times S'/S')\rightarrow T\rightarrow S'$ above
$T^*_{q|T}(H\times S'/S')\rightarrow T\rightarrow S'$ above ![]() $s=0$ (
$s=0$ (![]() $s$ is the coordinate on
$s$ is the coordinate on ![]() $S'$) is contained in
$S'$) is contained in ![]() $T^*H$ and is Lagrangian: indeed, it has dimension
$T^*H$ and is Lagrangian: indeed, it has dimension ![]() $\dim H$ since
$\dim H$ since ![]() $T^*_{s|T}(H\times S'/S')$ has dimension
$T^*_{s|T}(H\times S'/S')$ has dimension ![]() $\dim H+1$, and it is easily seen to be isotropic. We denote it by
$\dim H+1$, and it is easily seen to be isotropic. We denote it by ![]() $\Lambda _T$. The characteristic varieties of
$\Lambda _T$. The characteristic varieties of ![]() $\mathcal {N}_1$ and
$\mathcal {N}_1$ and ![]() $\mathcal {N}'_1$ are contained in the fiber above
$\mathcal {N}'_1$ are contained in the fiber above ![]() $s=0$ of
$s=0$ of ![]() $\operatorname {Char}\mathcal {M}_1$, hence in the union, over
$\operatorname {Char}\mathcal {M}_1$, hence in the union, over ![]() $Y,T$ occurring in
$Y,T$ occurring in ![]() $\operatorname {Char}\mathcal {N}$, of the Lagrangian subsets
$\operatorname {Char}\mathcal {N}$, of the Lagrangian subsets ![]() $T^*_YX\times \Lambda _T$, as claimed, because
$T^*_YX\times \Lambda _T$, as claimed, because ![]() $\Lambda$ is nothing but
$\Lambda$ is nothing but ![]() $\mathop {\textstyle \bigcup } _YT^*_YX$.
$\mathop {\textstyle \bigcup } _YT^*_YX$.
As a consequence, ![]() $\mathcal {N}_1$ is a regular holonomic
$\mathcal {N}_1$ is a regular holonomic ![]() $\mathcal {D}_{X\times H}$-module satisfying the assumption of the proposition, and
$\mathcal {D}_{X\times H}$-module satisfying the assumption of the proposition, and ![]() $\ker (s:\mathcal {M}\rightarrow \mathcal {M})$ is a coherent
$\ker (s:\mathcal {M}\rightarrow \mathcal {M})$ is a coherent ![]() $\mathcal {D}_{X\times H/H}$-submodule of it. We can thus apply the induction hypothesis to conclude that (3.22) holds for
$\mathcal {D}_{X\times H/H}$-submodule of it. We can thus apply the induction hypothesis to conclude that (3.22) holds for ![]() $\ker s$.
$\ker s$.
On the other hand, for each ![]() $k\geqslant 0$, by applying (3.21) to
$k\geqslant 0$, by applying (3.21) to ![]() $s^k\mathcal {M}_1$, we obtain, according to the claim, that
$s^k\mathcal {M}_1$, we obtain, according to the claim, that ![]() $s^k\mathcal {M}_1/s^{k+1}\mathcal {M}_1$ is a regular holonomic
$s^k\mathcal {M}_1/s^{k+1}\mathcal {M}_1$ is a regular holonomic ![]() $\mathcal {D}_{X\times H}$-module with characteristic variety contained in
$\mathcal {D}_{X\times H}$-module with characteristic variety contained in ![]() $\Lambda \times T^*H$. Then
$\Lambda \times T^*H$. Then
is a coherent ![]() $\mathcal {D}_{X\times H/H}$-submodule of
$\mathcal {D}_{X\times H/H}$-submodule of ![]() $s^k\mathcal {M}_1/s^{k+1}\mathcal {M}_1$. The induction hypothesis implies that
$s^k\mathcal {M}_1/s^{k+1}\mathcal {M}_1$. The induction hypothesis implies that ![]() $\mathcal {M}^{(k)}$ is
$\mathcal {M}^{(k)}$ is ![]() $\mathcal {D}_{X\times H/H}$-regular holonomic. It follows by Proposition 3.2(iii) that
$\mathcal {D}_{X\times H/H}$-regular holonomic. It follows by Proposition 3.2(iii) that ![]() $\mathcal {M}/(\mathcal {M}\cap s^{k+1}\mathcal {M}_1)$ is also a regular holonomic
$\mathcal {M}/(\mathcal {M}\cap s^{k+1}\mathcal {M}_1)$ is also a regular holonomic ![]() $\mathcal {D}_{X\times H/H}$-module. It remains to note that coherence implies that, locally on
$\mathcal {D}_{X\times H/H}$-module. It remains to note that coherence implies that, locally on ![]() $X$, there exists
$X$, there exists ![]() $k$ such that
$k$ such that ![]() $\mathcal {M}\cap s^{k+1}\mathcal {M}_1 \subset s\mathcal {M}$, so that
$\mathcal {M}\cap s^{k+1}\mathcal {M}_1 \subset s\mathcal {M}$, so that ![]() $\mathcal {M}/s\mathcal {M}$ is a coherent quotient of a regular holonomic
$\mathcal {M}/s\mathcal {M}$ is a coherent quotient of a regular holonomic ![]() $\mathcal {D}_{X\times H/H}$-module. Again by Proposition 3.2(iii) it is also a regular holonomic
$\mathcal {D}_{X\times H/H}$-module. Again by Proposition 3.2(iii) it is also a regular holonomic ![]() $\mathcal {D}_{X\times H/H}$-module, concluding the proof of (3.22).
$\mathcal {D}_{X\times H/H}$-module, concluding the proof of (3.22).
Proof of (3.21) We consider the Kashiwara–Malgrange ![]() $V$-filtration
$V$-filtration ![]() $V_{\scriptscriptstyle \bullet }\mathcal {N}$ of
$V_{\scriptscriptstyle \bullet }\mathcal {N}$ of ![]() $\mathcal {N}$ relative to the function
$\mathcal {N}$ relative to the function ![]() $s$ (cf., e.g., [Reference Mebkhout and SabbahMS89, Reference Maisonobe and MebkhoutMM04]). This is an increasing filtration indexed by
$s$ (cf., e.g., [Reference Mebkhout and SabbahMS89, Reference Maisonobe and MebkhoutMM04]). This is an increasing filtration indexed by ![]() $\mathbb {Z}$ which satisfies, owing to the regularity of
$\mathbb {Z}$ which satisfies, owing to the regularity of ![]() $\mathcal {N}$, the following properties:
$\mathcal {N}$, the following properties:
•
 $V_k\mathcal {N}$ is
$V_k\mathcal {N}$ is  $\mathcal {D}_{X\times S/S}$-coherent for any
$\mathcal {D}_{X\times S/S}$-coherent for any  $k\in \mathbb {Z}$ (see [Reference Mebkhout and SabbahMS89, Theorem (4.12.1)]);
$k\in \mathbb {Z}$ (see [Reference Mebkhout and SabbahMS89, Theorem (4.12.1)]);• for each
 $k\in \mathbb {Z}$,
$k\in \mathbb {Z}$,  $s(V_k\mathcal {N})\subset V_{k-1}\mathcal {N}$ and for
$s(V_k\mathcal {N})\subset V_{k-1}\mathcal {N}$ and for  $k\leqslant -1$, the multiplication by
$k\leqslant -1$, the multiplication by  $s$ on
$s$ on  $V_k\mathcal {N}$ is injective with image
$V_k\mathcal {N}$ is injective with image  $V_{k-1}\mathcal {N}$ (cf., e.g., [Reference Mebkhout and SabbahMS89, Proposition (4.5.2)]);
$V_{k-1}\mathcal {N}$ (cf., e.g., [Reference Mebkhout and SabbahMS89, Proposition (4.5.2)]);• each
 $\mathrm {gr}_k^V\mathcal {N}$ is a regular holonomic
$\mathrm {gr}_k^V\mathcal {N}$ is a regular holonomic  $\mathcal {D}_{X}$-module (cf., e.g., [Reference Maisonobe and MebkhoutMM04, Corollary 4.7-5]).
$\mathcal {D}_{X}$-module (cf., e.g., [Reference Maisonobe and MebkhoutMM04, Corollary 4.7-5]).
From the second point we deduce that, for ![]() $k\leqslant -1$,
$k\leqslant -1$, ![]() $Li_{s_o}^*V_k\mathcal {N}=i_{s_o}^*V_k\mathcal {N}=\mathrm {gr}_k^V\mathcal {N}$, and by the third point the latter is
$Li_{s_o}^*V_k\mathcal {N}=i_{s_o}^*V_k\mathcal {N}=\mathrm {gr}_k^V\mathcal {N}$, and by the third point the latter is ![]() $\mathcal {D}_{X}$-regular holonomic. For
$\mathcal {D}_{X}$-regular holonomic. For ![]() $k\geqslant 0$,
$k\geqslant 0$, ![]() $V_k\mathcal {N}$ is a successive extension of
$V_k\mathcal {N}$ is a successive extension of ![]() $V_{-1}\mathcal {N}$ by regular holonomic
$V_{-1}\mathcal {N}$ by regular holonomic ![]() $\mathcal {D}_{X}$-modules
$\mathcal {D}_{X}$-modules ![]() $\mathrm {gr}_\ell ^V\mathcal {N}$. Therefore, for each
$\mathrm {gr}_\ell ^V\mathcal {N}$. Therefore, for each ![]() $k$, the kernel and cokernel of
$k$, the kernel and cokernel of ![]() $s:V_k\mathcal {N}\rightarrow V_k\mathcal {N}$ are
$s:V_k\mathcal {N}\rightarrow V_k\mathcal {N}$ are ![]() $\mathcal {D}_{X}$-regular holonomic: this is proved by induction on
$\mathcal {D}_{X}$-regular holonomic: this is proved by induction on ![]() $k$ since it is clear for
$k$ since it is clear for ![]() $k<0$, and the inductive step follows by considering the snake lemma applied to the following commutative diagram of exact sequences.
$k<0$, and the inductive step follows by considering the snake lemma applied to the following commutative diagram of exact sequences.

We deduce that ![]() $sV_k\mathcal {N}/s^\ell V_k$ is regular holonomic for any
$sV_k\mathcal {N}/s^\ell V_k$ is regular holonomic for any ![]() $\ell \geqslant 1$. As any
$\ell \geqslant 1$. As any ![]() $\mathcal {D}_{X\times S/S}$-coherent submodule of
$\mathcal {D}_{X\times S/S}$-coherent submodule of ![]() $\mathcal {N}$, locally on
$\mathcal {N}$, locally on ![]() $X\times S$,
$X\times S$, ![]() $\mathcal {M}$ is contained in
$\mathcal {M}$ is contained in ![]() $V_k\mathcal {N}$ for some
$V_k\mathcal {N}$ for some ![]() $k\gg 0$ and, by the Artin–Rees lemma,
$k\gg 0$ and, by the Artin–Rees lemma, ![]() $s\mathcal {M}$ contains
$s\mathcal {M}$ contains ![]() $\mathcal {M}\cap s^\ell V_k\mathcal {N}$ for some
$\mathcal {M}\cap s^\ell V_k\mathcal {N}$ for some ![]() $\ell \geqslant 1$. Since
$\ell \geqslant 1$. Since ![]() $\ker (s:\mathcal {M}\rightarrow \mathcal {M})$ is contained in
$\ker (s:\mathcal {M}\rightarrow \mathcal {M})$ is contained in ![]() $\ker ( s:V_k\mathcal {N}\rightarrow V_k\mathcal {N})$, the former is regular holonomic because the latter is so. On the other hand, by considering the inclusion and the quotient maps
$\ker ( s:V_k\mathcal {N}\rightarrow V_k\mathcal {N})$, the former is regular holonomic because the latter is so. On the other hand, by considering the inclusion and the quotient maps
we conclude that ![]() $(\mathcal {M}\cap sV_k\mathcal {N})/s\mathcal {M}$ is also
$(\mathcal {M}\cap sV_k\mathcal {N})/s\mathcal {M}$ is also ![]() $\mathcal {D}_{X}$-regular holonomic. Furthermore, by considering the exact sequence
$\mathcal {D}_{X}$-regular holonomic. Furthermore, by considering the exact sequence
we conclude that ![]() $\mathcal {M}/s\mathcal {M}$ is
$\mathcal {M}/s\mathcal {M}$ is ![]() $\mathcal {D}_{X}$-regular holonomic.
$\mathcal {D}_{X}$-regular holonomic.
4. Holonomic  $\mathcal {D}_{X\times S/S}$-modules of D-type and applications
$\mathcal {D}_{X\times S/S}$-modules of D-type and applications
4.a  $S$-locally constant sheaves and their associated relative connections
$S$-locally constant sheaves and their associated relative connections
Let ![]() $X$ be a connected complex manifold and let
$X$ be a connected complex manifold and let ![]() $L$ be an
$L$ be an ![]() $S$-locally constant sheaf of
$S$-locally constant sheaf of ![]() $p^{-1}\mathcal {O}_S$-modules on
$p^{-1}\mathcal {O}_S$-modules on ![]() $X\times S$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Appendix]). For any
$X\times S$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Appendix]). For any ![]() $x_o\in X$,
$x_o\in X$, ![]() $L$ is uniquely determined from a monodromy representation
$L$ is uniquely determined from a monodromy representation ![]() $\pi _1(X,x_o)\rightarrow \operatorname {Aut}_{\mathcal {O}_S}(G)$ with
$\pi _1(X,x_o)\rightarrow \operatorname {Aut}_{\mathcal {O}_S}(G)$ with ![]() $G=i_{x_o}^{-1}L$. As a consequence, there exists an
$G=i_{x_o}^{-1}L$. As a consequence, there exists an ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $G$ such that, for any
$G$ such that, for any ![]() $1$-connected open subset
$1$-connected open subset ![]() $U$ of
$U$ of ![]() $X\times S$, there exists an isomorphism
$X\times S$, there exists an isomorphism ![]() $L_{|U\times S}\simeq p_U^{-1}G$. Two choices of
$L_{|U\times S}\simeq p_U^{-1}G$. Two choices of ![]() $G$ are isomorphic, but non-canonically in general. Furthermore,
$G$ are isomorphic, but non-canonically in general. Furthermore, ![]() $L$ is
$L$ is ![]() $p^{-1}\mathcal {O}_S$-coherent if and only if
$p^{-1}\mathcal {O}_S$-coherent if and only if ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-coherent.
$\mathcal {O}_S$-coherent.
To any ![]() $S$-locally constant sheaf
$S$-locally constant sheaf ![]() $L$ one can associate an exact sequence of sheaves of
$L$ one can associate an exact sequence of sheaves of ![]() $p^{-1}\mathcal {O}_S$-modules
$p^{-1}\mathcal {O}_S$-modules
where ![]() $L_\mathrm {t}$ denotes the subsheaf of
$L_\mathrm {t}$ denotes the subsheaf of ![]() $p^{-1}\mathcal {O}_S$-torsion and
$p^{-1}\mathcal {O}_S$-torsion and ![]() $L_\mathrm {tf}$ the maximal
$L_\mathrm {tf}$ the maximal ![]() $p^{-1}\mathcal {O}_S$-torsion-free quotient. Then
$p^{-1}\mathcal {O}_S$-torsion-free quotient. Then ![]() $L_\mathrm {t}$ and
$L_\mathrm {t}$ and ![]() $L_\mathrm {tf}$ are
$L_\mathrm {tf}$ are ![]() $S$-locally constant and the previous exact sequence yields (for any choice of
$S$-locally constant and the previous exact sequence yields (for any choice of ![]() $G$) to the exact sequence of
$G$) to the exact sequence of ![]() $\mathcal {O}_{S}$-modules
$\mathcal {O}_{S}$-modules
with ![]() $G_\mathrm {t}$ and
$G_\mathrm {t}$ and ![]() $G_\mathrm {tf}$ defined similarly. The following is straightforward.
$G_\mathrm {tf}$ defined similarly. The following is straightforward.
Lemma 4.2 Let ![]() $\pi :S\rightarrow S'$ be a holomorphic map between complex manifolds.
$\pi :S\rightarrow S'$ be a holomorphic map between complex manifolds.
(i) If
 $L$ is an
$L$ is an  $S$-locally constant sheaf on
$S$-locally constant sheaf on  $X\times S$ with associated
$X\times S$ with associated  $\mathcal {O}_S$-module
$\mathcal {O}_S$-module  $G$, then
$G$, then  $\pi _!L$ is
$\pi _!L$ is  $S'$-locally constant on
$S'$-locally constant on  $X\times S'$ and
$X\times S'$ and  $\pi _!G$ is an associated
$\pi _!G$ is an associated  $\mathcal {O}_{S'}$-module to
$\mathcal {O}_{S'}$-module to  $\pi _!L$.
$\pi _!L$.(ii) If
 $L'$ is an
$L'$ is an  $S'$-locally constant sheaf on
$S'$-locally constant sheaf on  $X\times S'$ with associated
$X\times S'$ with associated  $\mathcal {O}_S'$-module
$\mathcal {O}_S'$-module  $G'$, then
$G'$, then  $\pi ^*L'$ is
$\pi ^*L'$ is  $S$-locally constant on
$S$-locally constant on  $X\times S$ and
$X\times S$ and  $\pi ^*G'$ is an associated
$\pi ^*G'$ is an associated  $\mathcal {O}_S$-module to
$\mathcal {O}_S$-module to  $\pi ^*L'$.
$\pi ^*L'$.
We denote by ![]() $\mathrm {d}_{X\times S/S}:\mathcal {O}_{X\times S}\rightarrow \Omega ^1_{X\times S/S}$ the relative differential associated to
$\mathrm {d}_{X\times S/S}:\mathcal {O}_{X\times S}\rightarrow \Omega ^1_{X\times S/S}$ the relative differential associated to ![]() $p$. Let us recall the Riemann–Hilbert correspondence for coherent
$p$. Let us recall the Riemann–Hilbert correspondence for coherent ![]() $S$-local systems proved in [Reference DeligneDel70, Theorem 2.23 p. 14], in the particular case of a projection
$S$-local systems proved in [Reference DeligneDel70, Theorem 2.23 p. 14], in the particular case of a projection ![]() $X\times S\rightarrow S$, where
$X\times S\rightarrow S$, where ![]() $X$ and
$X$ and ![]() $S$ are complex manifolds.
$S$ are complex manifolds.
The functor ![]() $L\mapsto (E_L,\nabla )=(\mathcal {O}_{X\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X\times S/S}\otimes \operatorname {Id})$ induces an equivalence between the category of coherent
$L\mapsto (E_L,\nabla )=(\mathcal {O}_{X\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X\times S/S}\otimes \operatorname {Id})$ induces an equivalence between the category of coherent ![]() $S$-locally constant sheaves of
$S$-locally constant sheaves of ![]() $p^{-1}\mathcal {O}_S$-modules and the category of coherent
$p^{-1}\mathcal {O}_S$-modules and the category of coherent ![]() $\mathcal {O}_{X\times S}$-modules
$\mathcal {O}_{X\times S}$-modules ![]() $E$ equipped with an integrable relative connection
$E$ equipped with an integrable relative connection
A quasi-inverse is given by ![]() $(E,\nabla )\mapsto E^\nabla =\ker \nabla$. The monodromy representation attached to the coherent
$(E,\nabla )\mapsto E^\nabla =\ker \nabla$. The monodromy representation attached to the coherent ![]() $S$-locally constant sheaf
$S$-locally constant sheaf ![]() $E^{\nabla }$ is also called the monodromy representation of
$E^{\nabla }$ is also called the monodromy representation of ![]() $\nabla$ on
$\nabla$ on ![]() $E$. Let us emphasize a direct consequence.
$E$. Let us emphasize a direct consequence.
Corollary 4.3 Let ![]() $(E,\nabla )$ be a coherent
$(E,\nabla )$ be a coherent ![]() $\mathcal {O}_{X\times S}$-module equipped with an integrable relative connection. Then the natural
$\mathcal {O}_{X\times S}$-module equipped with an integrable relative connection. Then the natural ![]() $\mathcal {O}_{X\times S}$-linear morphism
$\mathcal {O}_{X\times S}$-linear morphism
is an isomorphism compatible with the integrable connections ![]() $\mathrm {d}_{X\times S/S}\otimes \operatorname {Id}$ and
$\mathrm {d}_{X\times S/S}\otimes \operatorname {Id}$ and ![]() $\nabla$.
$\nabla$.
Proposition 4.4 Notation as in Lemma 4.2.
(i) Let
 $L$ be a coherent
$L$ be a coherent  $S$-locally constant sheaf. If
$S$-locally constant sheaf. If  $\pi$ is proper, then
$\pi$ is proper, then  $\pi _*L$ is
$\pi _*L$ is  $S'$-coherent and there exists a natural morphism
$S'$-coherent and there exists a natural morphism  $E_{\pi _*L}\rightarrow \pi _*E_L.$
$E_{\pi _*L}\rightarrow \pi _*E_L.$(ii) Let
 $L'$ be a coherent
$L'$ be a coherent  $S'$-locally constant sheaf. Then
$S'$-locally constant sheaf. Then  $E_{\pi ^*L'}\simeq \pi ^*(E_{L'})$.
$E_{\pi ^*L'}\simeq \pi ^*(E_{L'})$.
Proof. (i) As ![]() $\pi$ is proper,
$\pi$ is proper, ![]() $\pi _*L$ is a coherent
$\pi _*L$ is a coherent ![]() $S'$-locally constant sheaf on
$S'$-locally constant sheaf on ![]() $X\times S'$ (Lemma 4.2(i) and Grauert's theorem). The natural morphism
$X\times S'$ (Lemma 4.2(i) and Grauert's theorem). The natural morphism ![]() $\mathcal {O}_{X\times S'}\rightarrow \pi _*\mathcal {O}_{X\times S}$ induces a composed morphism
$\mathcal {O}_{X\times S'}\rightarrow \pi _*\mathcal {O}_{X\times S}$ induces a composed morphism
which is clearly compatible with the relative differential ![]() $\mathrm {d}\otimes \operatorname {Id}$. We note that if
$\mathrm {d}\otimes \operatorname {Id}$. We note that if ![]() $\pi$ is surjective with connected fibers, the first morphism is an isomorphism because
$\pi$ is surjective with connected fibers, the first morphism is an isomorphism because ![]() $\mathcal {O}_{X\times S'}\rightarrow \pi _*\mathcal {O}_{X\times S}$ is then an isomorphism. This is the case if for example
$\mathcal {O}_{X\times S'}\rightarrow \pi _*\mathcal {O}_{X\times S}$ is then an isomorphism. This is the case if for example ![]() $S'$ is a complex manifold and
$S'$ is a complex manifold and ![]() $\pi$ is a proper modification of
$\pi$ is a proper modification of ![]() $S'$.
$S'$.
(ii) The second point is straightforward.
4.b The Deligne extension of an  $S$-locally constant sheaf
$S$-locally constant sheaf
We recall Theorem 2.6 and extend Corollary 2.8 of [Reference Monteiro Fernandes and SabbahMFS19] to the case where ![]() $\dim S>1$.
$\dim S>1$.
Notation 4.5 Let ![]() $Y$ be a hypersurface in
$Y$ be a hypersurface in ![]() $X$ (assumed to be connected) and let us denote the inclusion by
$X$ (assumed to be connected) and let us denote the inclusion by ![]() $j:X^*:=X\smallsetminus Y\mathrel {\hookrightarrow} X$. Let
$j:X^*:=X\smallsetminus Y\mathrel {\hookrightarrow} X$. Let ![]() $L$ be a coherent
$L$ be a coherent ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$. Let
$X^*\times S$. Let ![]() $(E_L,\nabla )=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$ be the associated coherent
$(E_L,\nabla )=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$ be the associated coherent ![]() $\mathcal {O}_{X^*\times S}$-module with flat relative connection
$\mathcal {O}_{X^*\times S}$-module with flat relative connection ![]() $\nabla =\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id}$, so that
$\nabla =\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id}$, so that ![]() $L=E_L^\nabla$. We simply set
$L=E_L^\nabla$. We simply set ![]() $E=E_L$ when the context is clear, that we consider as a left
$E=E_L$ when the context is clear, that we consider as a left ![]() $\mathcal {D}_{X^*\times S/S}$-module. We sometimes call
$\mathcal {D}_{X^*\times S/S}$-module. We sometimes call ![]() $L$ a coherent
$L$ a coherent ![]() $S$-local system.
$S$-local system.
Lemma 4.6 The functor ![]() $j_*E_{\scriptscriptstyle \bullet }:L\mapsto j_*E_L$ with values in
$j_*E_{\scriptscriptstyle \bullet }:L\mapsto j_*E_L$ with values in ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ is exact.
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ is exact.
Proof. Any ![]() $(x_o,s_o)\in Y\times S$ has a fundamental system of open neighborhood
$(x_o,s_o)\in Y\times S$ has a fundamental system of open neighborhood ![]() $U\times U(s_o)$ such that
$U\times U(s_o)$ such that ![]() $(U\smallsetminus D)\times U(s_o)$ is Stein. As
$(U\smallsetminus D)\times U(s_o)$ is Stein. As ![]() $E_L$ is
$E_L$ is ![]() $\mathcal {O}_{X^*\times S}$-coherent, the result follows.
$\mathcal {O}_{X^*\times S}$-coherent, the result follows.
We assume from now on that ![]() $Y=D$ is a divisor with normal crossings in
$Y=D$ is a divisor with normal crossings in ![]() $X$. Let
$X$. Let ![]() $\varpi :\widetilde X\rightarrow X$ denote the real blowing up of
$\varpi :\widetilde X\rightarrow X$ denote the real blowing up of ![]() $X$ along the components of
$X$ along the components of ![]() $D$. We denote by
$D$. We denote by ![]() $\widetilde \jmath :X^*\mathrel {\hookrightarrow}\widetilde X$ the inclusion, so that
$\widetilde \jmath :X^*\mathrel {\hookrightarrow}\widetilde X$ the inclusion, so that ![]() $j=\varpi \circ \widetilde \jmath$. Let
$j=\varpi \circ \widetilde \jmath$. Let ![]() $x_o\in D$,
$x_o\in D$, ![]() $\widetilde x_o\in \varpi ^{-1}(x_o)$ and let
$\widetilde x_o\in \varpi ^{-1}(x_o)$ and let ![]() $s_o\in S$. Choose local coordinates
$s_o\in S$. Choose local coordinates ![]() $(x_1,\ldots,x_n)$ at
$(x_1,\ldots,x_n)$ at ![]() $x_o$ such that
$x_o$ such that ![]() $D=\{x_1\cdots x_\ell =0\}$ and consider the associated polar coordinates
$D=\{x_1\cdots x_\ell =0\}$ and consider the associated polar coordinates ![]() $(\boldsymbol {\rho },\boldsymbol {\theta },\boldsymbol {x}'):=(\rho _1,\theta _1,\ldots,\rho _\ell,\theta _\ell,x_{\ell +1},\ldots,x_n)$ so that
$(\boldsymbol {\rho },\boldsymbol {\theta },\boldsymbol {x}'):=(\rho _1,\theta _1,\ldots,\rho _\ell,\theta _\ell,x_{\ell +1},\ldots,x_n)$ so that ![]() $\widetilde x_o$ has coordinates
$\widetilde x_o$ has coordinates ![]() $\boldsymbol {\rho }_o=0$,
$\boldsymbol {\rho }_o=0$, ![]() $\boldsymbol {\theta }_o$,
$\boldsymbol {\theta }_o$, ![]() $\boldsymbol {x}'_o=0$. We also denote by
$\boldsymbol {x}'_o=0$. We also denote by ![]() $\varpi$ the induced map
$\varpi$ the induced map ![]() $\widetilde X\times S\to X\times S$ and by
$\widetilde X\times S\to X\times S$ and by ![]() $\widetilde p:\widetilde X\times S\rightarrow S$ the projection.
$\widetilde p:\widetilde X\times S\rightarrow S$ the projection.
Definition 4.7 The subsheaf ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ of
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ of ![]() $\widetilde \jmath _*\mathcal {O}_{X^*\times S}$ of holomorphic functions having moderate growth along
$\widetilde \jmath _*\mathcal {O}_{X^*\times S}$ of holomorphic functions having moderate growth along ![]() $\varpi ^{-1}(D)$ is defined by the following two requirements:
$\varpi ^{-1}(D)$ is defined by the following two requirements:
•
 $\widetilde \jmath ^{-1}\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\mathcal {O}_{X^*\times S}$;
$\widetilde \jmath ^{-1}\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\mathcal {O}_{X^*\times S}$;• for any
 $x_o\in D$,
$x_o\in D$,  $\widetilde x_o\in \varpi ^{-1}(x_o)$ and
$\widetilde x_o\in \varpi ^{-1}(x_o)$ and  $s_o\in S$, a germ
$s_o\in S$, a germ  $\widetilde h\in (\widetilde \jmath _*\mathcal {O}_{X^*\times S})_{(\widetilde x_o,s_o)}$ is said to have moderate growth, i.e., to belong to
$\widetilde h\in (\widetilde \jmath _*\mathcal {O}_{X^*\times S})_{(\widetilde x_o,s_o)}$ is said to have moderate growth, i.e., to belong to  $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S,(\widetilde x_o,s_o)}$, if there exist open sets
(4.8)(
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S,(\widetilde x_o,s_o)}$, if there exist open sets
(4.8)( \begin{equation} \widetilde U_\varepsilon:=\{\Vert\boldsymbol{\rho}\Vert<\varepsilon, \Vert\boldsymbol{x}'\Vert<\varepsilon,\Vert\boldsymbol{\theta}- \boldsymbol{\theta}_o\Vert<\varepsilon\}\quad\text{and}\quad U(s_o)\ni s_o \end{equation}
\begin{equation} \widetilde U_\varepsilon:=\{\Vert\boldsymbol{\rho}\Vert<\varepsilon, \Vert\boldsymbol{x}'\Vert<\varepsilon,\Vert\boldsymbol{\theta}- \boldsymbol{\theta}_o\Vert<\varepsilon\}\quad\text{and}\quad U(s_o)\ni s_o \end{equation} $\varepsilon$ small enough) such that, setting
$\varepsilon$ small enough) such that, setting  $U^*_\varepsilon :=\widetilde U_\varepsilon \smallsetminus \{\rho _1\cdots \rho _\ell =0\}$,
$U^*_\varepsilon :=\widetilde U_\varepsilon \smallsetminus \{\rho _1\cdots \rho _\ell =0\}$,  $\widetilde h$ is defined on
$\widetilde h$ is defined on  $U^*_\varepsilon \times U(s_o)$ and
$U^*_\varepsilon \times U(s_o)$ and  $|\widetilde h|$ is bounded on this open set by
$|\widetilde h|$ is bounded on this open set by  $C\Vert \boldsymbol {\rho }\Vert ^{-N}$, for some
$C\Vert \boldsymbol {\rho }\Vert ^{-N}$, for some  $C,N>0$.
$C,N>0$.
We recall the following properties of the sheaf ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$:
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$:
(i)
 $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ is a
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ is a  $\varpi ^{-1}\mathcal {D}_{X\times S/S}(*D)$-module (cf. [Reference SabbahSab00, § 1.1.6]) which is
$\varpi ^{-1}\mathcal {D}_{X\times S/S}(*D)$-module (cf. [Reference SabbahSab00, § 1.1.6]) which is  $\varpi ^{-1}\mathcal {O}_{X\times S}$-flat (cf. [Reference MochizukiMoc14, Theorem 4.6.1]);
$\varpi ^{-1}\mathcal {O}_{X\times S}$-flat (cf. [Reference MochizukiMoc14, Theorem 4.6.1]);(ii) for any coherent
 $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module  $M$, the natural morphism
is injective (cf. [Reference MochizukiMoc14, Theorem 4.6.1]);
$M$, the natural morphism
is injective (cf. [Reference MochizukiMoc14, Theorem 4.6.1]); \[ \mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\varpi^{-1}\mathcal{O}_{X\times S}}\varpi^{-1}M\longrightarrow\widetilde\jmath_*j^{-1}M \]
\[ \mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\varpi^{-1}\mathcal{O}_{X\times S}}\varpi^{-1}M\longrightarrow\widetilde\jmath_*j^{-1}M \]
(iii)
 $R\varpi _*\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\varpi _*\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\mathcal {O}_{X\times S}(*D)$ (cf. [Reference SabbahSab00, Corollary II.1.1.18]).
$R\varpi _*\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\varpi _*\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}=\mathcal {O}_{X\times S}(*D)$ (cf. [Reference SabbahSab00, Corollary II.1.1.18]).
Let us already note for later use that these properties imply, for any ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $G$,
$G$,
Indeed, we have
 \begin{align*} R\varpi_*\Big(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big) &\simeq R\varpi_*\Big(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes^L_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big) \quad\text{by property (i)}\\ &\simeq R\varpi_*(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S})\otimes^L_{p^{-1}\mathcal{O}_S} p^{-1}G\\ &\simeq\mathcal{O}_{X\times S}(*D)\otimes^L_{p^{-1}\mathcal{O}_S}p^{-1}G\quad\text{by property (iii)}\\ &\simeq\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G, \end{align*}
\begin{align*} R\varpi_*\Big(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big) &\simeq R\varpi_*\Big(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes^L_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big) \quad\text{by property (i)}\\ &\simeq R\varpi_*(\mathcal{A}^\mathrm{mod}_{\widetilde X\times S})\otimes^L_{p^{-1}\mathcal{O}_S} p^{-1}G\\ &\simeq\mathcal{O}_{X\times S}(*D)\otimes^L_{p^{-1}\mathcal{O}_S}p^{-1}G\quad\text{by property (iii)}\\ &\simeq\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G, \end{align*}
where the latter isomorphism follows from flatness of ![]() $\mathcal {O}_{X\times S}(*D)$ over
$\mathcal {O}_{X\times S}(*D)$ over ![]() $p^{-1}\mathcal {O}_S$. Furthermore, property (ii) implies that, for any coherent
$p^{-1}\mathcal {O}_S$. Furthermore, property (ii) implies that, for any coherent ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $G$, the natural morphism
$G$, the natural morphism
is injective.
Note that, ![]() $U^*_\varepsilon$ being contractible, we have
$U^*_\varepsilon$ being contractible, we have ![]() $L_{|U^*_\varepsilon \times U(s_o)}\simeq p^{-1}_{U^*_\varepsilon }G_{|U(s_o)}$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Proposition A.12]). We thus have an identification
$L_{|U^*_\varepsilon \times U(s_o)}\simeq p^{-1}_{U^*_\varepsilon }G_{|U(s_o)}$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Proposition A.12]). We thus have an identification
 \begin{align} (\widetilde\jmath_*E)_{|\widetilde U_\varepsilon\times U(s_o)}&\simeq\widetilde\jmath_* \Big(\mathcal{O}_{U^*_\varepsilon\times U(s_o)}\otimes_{p^{-1} \mathcal{O}_{U(s_o)}} p^{-1}_{U^*_\varepsilon}G_{|U(s_o)},\mathrm{d}_{U^*_\varepsilon \times U(s_o)/U(s_o)}\otimes \operatorname{Id}\Big)\nonumber\\ &\overset\sim\longleftarrow \Big((\widetilde\jmath_*\mathcal{O}_{U^*_\varepsilon\times U(s_o)})\otimes_{\widetilde p^{-1} \mathcal{O}_{U(s_o)}}\widetilde p^{-1}_{\widetilde U_\varepsilon}G_{|U(s_o)}, \mathrm{d}_{\widetilde U_\varepsilon\times U(s_o)/U(s_o)}\otimes \operatorname{Id}\Big). \end{align}
\begin{align} (\widetilde\jmath_*E)_{|\widetilde U_\varepsilon\times U(s_o)}&\simeq\widetilde\jmath_* \Big(\mathcal{O}_{U^*_\varepsilon\times U(s_o)}\otimes_{p^{-1} \mathcal{O}_{U(s_o)}} p^{-1}_{U^*_\varepsilon}G_{|U(s_o)},\mathrm{d}_{U^*_\varepsilon \times U(s_o)/U(s_o)}\otimes \operatorname{Id}\Big)\nonumber\\ &\overset\sim\longleftarrow \Big((\widetilde\jmath_*\mathcal{O}_{U^*_\varepsilon\times U(s_o)})\otimes_{\widetilde p^{-1} \mathcal{O}_{U(s_o)}}\widetilde p^{-1}_{\widetilde U_\varepsilon}G_{|U(s_o)}, \mathrm{d}_{\widetilde U_\varepsilon\times U(s_o)/U(s_o)}\otimes \operatorname{Id}\Big). \end{align}
Indeed, for a polysector ![]() $\widetilde V_\varepsilon \subset \widetilde U_\varepsilon$ and
$\widetilde V_\varepsilon \subset \widetilde U_\varepsilon$ and ![]() $V\subset U(s_o)$, the natural morphism
$V\subset U(s_o)$, the natural morphism
is an isomorphism, because the adjunction morphism ![]() $p_{W*}p_W^{-1}G\rightarrow G$ is an isomorphism for both
$p_{W*}p_W^{-1}G\rightarrow G$ is an isomorphism for both ![]() $W=V_\varepsilon ^*$ and
$W=V_\varepsilon ^*$ and ![]() $W=\widetilde V_\varepsilon$ (both being connected, cf., e.g., [Reference Monteiro Fernandes and SabbahMFS19, Proposition A.1(2)]). The assertion is obtained by passing from the pre-sheaf isomorphism to a sheaf isomorphism.
$W=\widetilde V_\varepsilon$ (both being connected, cf., e.g., [Reference Monteiro Fernandes and SabbahMFS19, Proposition A.1(2)]). The assertion is obtained by passing from the pre-sheaf isomorphism to a sheaf isomorphism.
Definition 4.11 (The Deligne extension)
Let ![]() $x_o\in X$,
$x_o\in X$, ![]() $\widetilde x_o\in \varpi ^{-1}(x_o)$ and
$\widetilde x_o\in \varpi ^{-1}(x_o)$ and ![]() $s_o\in S$.
$s_o\in S$.
(i) A germ
 $\widetilde v$ of
$\widetilde v$ of  $(\widetilde \jmath _*E_L)_{(\widetilde x_o,s_o)}$ is said to have moderate growth if for some open set
$(\widetilde \jmath _*E_L)_{(\widetilde x_o,s_o)}$ is said to have moderate growth if for some open set  $\widetilde U_\varepsilon \times U(s_o)$ as above, and for some (equivalently, any) identification
$\widetilde U_\varepsilon \times U(s_o)$ as above, and for some (equivalently, any) identification  $L_{|U^*_\varepsilon \times U(s_o)}\simeq p^{-1}_{U^*_\varepsilon }G_{|U(s_o)}$,
$L_{|U^*_\varepsilon \times U(s_o)}\simeq p^{-1}_{U^*_\varepsilon }G_{|U(s_o)}$,  $\widetilde v$ belongs to the image of the injective morphism
$\widetilde v$ belongs to the image of the injective morphism
 \[ \Gamma\Big(\widetilde U_\varepsilon\times U(s_o);\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big)\longrightarrow\Gamma(\widetilde U_\varepsilon\times U(s_o);\widetilde\jmath_*E_L). \]
\[ \Gamma\Big(\widetilde U_\varepsilon\times U(s_o);\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G\Big)\longrightarrow\Gamma(\widetilde U_\varepsilon\times U(s_o);\widetilde\jmath_*E_L). \]
(ii) A germ
 $v$ of
$v$ of  $(j_*E_L)_{(x_o,s_o)}$ is said to have moderate growth if for each
$(j_*E_L)_{(x_o,s_o)}$ is said to have moderate growth if for each  $\widetilde x_o$ in
$\widetilde x_o$ in  $\varpi ^{-1}(x_o)$, the corresponding germ in
$\varpi ^{-1}(x_o)$, the corresponding germ in  $(\widetilde \jmath _*E_L)_{(\widetilde x_o,s_o)}$ has moderate growth. In particular, this holds for any local section of
$(\widetilde \jmath _*E_L)_{(\widetilde x_o,s_o)}$ has moderate growth. In particular, this holds for any local section of  $E_L$ at
$E_L$ at  $(x_o,s_o)$ if
$(x_o,s_o)$ if  $x_o\notin D$.
$x_o\notin D$.(iii) The subsheaf of
 $j_*E_L$ consisting of local sections whose germs have moderate growth is denoted by
$j_*E_L$ consisting of local sections whose germs have moderate growth is denoted by  $\widetilde E_L$. It satisfies
$\widetilde E_L$. It satisfies  $j^*\widetilde E_L=E_L$. It is called the Deligne extension of
$j^*\widetilde E_L=E_L$. It is called the Deligne extension of  $E_L$.
$E_L$.
Remark 4.12 By definition, with the previous notation, ![]() $v$ has moderate growth if and only if, on any such polysector
$v$ has moderate growth if and only if, on any such polysector ![]() $U_\varepsilon \times U(s_o)$, for any isomorphism
$U_\varepsilon \times U(s_o)$, for any isomorphism ![]() $L|_{U_\varepsilon ^*\times U(s_o)}\simeq p_{U_\varepsilon ^*}^{-1}G_{|U(s_o)}$, for any family of local generators
$L|_{U_\varepsilon ^*\times U(s_o)}\simeq p_{U_\varepsilon ^*}^{-1}G_{|U(s_o)}$, for any family of local generators ![]() $(g_j)$ of
$(g_j)$ of ![]() $G$ on
$G$ on ![]() $U(s_o)$,
$U(s_o)$, ![]() $v$ can be written as
$v$ can be written as ![]() $\sum _jv_j\otimes g_j$ with
$\sum _jv_j\otimes g_j$ with ![]() $v_j$ being holomorphic functions on the corresponding polysector in
$v_j$ being holomorphic functions on the corresponding polysector in ![]() $X^*\times S$ with moderate growth with respect to
$X^*\times S$ with moderate growth with respect to ![]() $D$.
$D$.
As ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ is stable by derivations with respect to
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$ is stable by derivations with respect to ![]() $X$,
$X$, ![]() $\widetilde E_L$ is a
$\widetilde E_L$ is a ![]() $\mathcal {D}_{X\times S/S}(*D)$-submodule of
$\mathcal {D}_{X\times S/S}(*D)$-submodule of ![]() $j_*E_L$.
$j_*E_L$.
Proposition 4.13 (First properties of the Deligne extension ![]() $\widetilde E_L$)
$\widetilde E_L$)
Let ![]() $L$ be a coherent
$L$ be a coherent ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$ and let
$X^*\times S$ and let ![]() $(E_L,\nabla )=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$ be the associated
$(E_L,\nabla )=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$ be the associated ![]() $\mathcal {O}_{X^*\times S}$-module with flat relative connection.
$\mathcal {O}_{X^*\times S}$-module with flat relative connection.
(i) The assignment
 $L\mapsto (\widetilde E_L,\nabla )$ with values in
$L\mapsto (\widetilde E_L,\nabla )$ with values in  $\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ is functorial.
$\mathrm {Mod}(\mathcal {D}_{X\times S/S})$ is functorial.(ii) Let
 $\pi :S\rightarrow S'$ be a proper holomorphic map. Then the natural morphism
$\pi :S\rightarrow S'$ be a proper holomorphic map. Then the natural morphism  $j_*(E_{\pi _*L},\nabla )\rightarrow \pi _*j_*(E_L,\nabla )$ sends the subsheaf
$j_*(E_{\pi _*L},\nabla )\rightarrow \pi _*j_*(E_L,\nabla )$ sends the subsheaf  $\widetilde E_{\pi _*L}$ to
$\widetilde E_{\pi _*L}$ to  $\pi _*\widetilde E_L$.
$\pi _*\widetilde E_L$.(iii) Let
 $\pi :S'\rightarrow S$ be a holomorphic map. Then the natural morphism
$\pi :S'\rightarrow S$ be a holomorphic map. Then the natural morphism  $\pi ^*j_*(E_L,\nabla )\rightarrow j_*(E_{\pi ^*L},\nabla )$ sends isomorphically
$\pi ^*j_*(E_L,\nabla )\rightarrow j_*(E_{\pi ^*L},\nabla )$ sends isomorphically  $\pi ^*(\widetilde E_L,\nabla )$ to
$\pi ^*(\widetilde E_L,\nabla )$ to  $(\widetilde E_{\pi ^*L},\nabla )$.
$(\widetilde E_{\pi ^*L},\nabla )$.
Proof. We only prove parts (i) and (ii), and part (iii) will be a consequence of Theorem 4.15.
(i) A morphism of ![]() $S$-locally constant sheaves
$S$-locally constant sheaves ![]() $\varphi :L\rightarrow L'$ defines a morphism
$\varphi :L\rightarrow L'$ defines a morphism ![]() $\varphi :E_L\rightarrow E_{L'}$ compatible with
$\varphi :E_L\rightarrow E_{L'}$ compatible with ![]() $\nabla$, hence
$\nabla$, hence ![]() $j_*E_L\rightarrow j_*E_{L'}$ compatible with
$j_*E_L\rightarrow j_*E_{L'}$ compatible with ![]() $\nabla$, and we only need to check that it sends
$\nabla$, and we only need to check that it sends ![]() $\widetilde E_L$ to
$\widetilde E_L$ to ![]() $\widetilde E_{L'}$. This is straightforward from the definition.
$\widetilde E_{L'}$. This is straightforward from the definition.
(ii) From the commutative diagram

together with the natural morphism of Proposition 4.2(i), we obtain the morphism ![]() $j_*(E_{\pi _*L},\nabla )\rightarrow \pi _*j_*(E_L,\nabla )$ and similarly
$j_*(E_{\pi _*L},\nabla )\rightarrow \pi _*j_*(E_L,\nabla )$ and similarly ![]() $\widetilde \jmath _*(E_{\pi _*L},\nabla )\rightarrow \pi _*\widetilde \jmath _*(E_L,\nabla )$. Let us consider an open subset
$\widetilde \jmath _*(E_{\pi _*L},\nabla )\rightarrow \pi _*\widetilde \jmath _*(E_L,\nabla )$. Let us consider an open subset ![]() $\widetilde U_\varepsilon \subset \widetilde X$ as in (4.8). Then
$\widetilde U_\varepsilon \subset \widetilde X$ as in (4.8). Then ![]() $U_\varepsilon ^*$ is contractible and for any
$U_\varepsilon ^*$ is contractible and for any ![]() $s'_o\in S'$,
$s'_o\in S'$, ![]() $L_{|U_\varepsilon ^*\times \pi ^{-1}(U(s'_o))}\simeq p_{U_\varepsilon ^*}^{-1}G_{|\pi ^{-1}(U(s'_o))}$. In order to simplify the notation, we set
$L_{|U_\varepsilon ^*\times \pi ^{-1}(U(s'_o))}\simeq p_{U_\varepsilon ^*}^{-1}G_{|\pi ^{-1}(U(s'_o))}$. In order to simplify the notation, we set ![]() $S'=U(s'_o)$ and
$S'=U(s'_o)$ and ![]() $S=\pi ^{-1}(U(s'_o))$. We also set
$S=\pi ^{-1}(U(s'_o))$. We also set ![]() $p=p_{\widetilde U_\varepsilon }$, so that
$p=p_{\widetilde U_\varepsilon }$, so that ![]() $p_{U_\varepsilon ^*}=p\circ \widetilde \jmath$. According to (4.10), we are led to proving that the natural morphism
$p_{U_\varepsilon ^*}=p\circ \widetilde \jmath$. According to (4.10), we are led to proving that the natural morphism
sends ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S'}\otimes _{\widetilde {p}^{\prime -1}\mathcal {O}_{S'}}\widetilde p^{\prime -1}\pi _*G$ to
$\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S'}\otimes _{\widetilde {p}^{\prime -1}\mathcal {O}_{S'}}\widetilde p^{\prime -1}\pi _*G$ to ![]() $\pi _*(\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S}\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G)$. Following the proof of Proposition 4.4(i), we are led to proving that the natural morphism
$\pi _*(\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S}\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G)$. Following the proof of Proposition 4.4(i), we are led to proving that the natural morphism ![]() $\widetilde \jmath _*\mathcal {O}_{U_\varepsilon ^*\times S'}\rightarrow \pi _*(\widetilde \jmath _*\mathcal {O}_{U_\varepsilon ^*\times S})$ sends
$\widetilde \jmath _*\mathcal {O}_{U_\varepsilon ^*\times S'}\rightarrow \pi _*(\widetilde \jmath _*\mathcal {O}_{U_\varepsilon ^*\times S})$ sends ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S'}$ to
$\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S'}$ to ![]() $\pi _*\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S}$. This follows from the definition of moderate growth, owing to the properness of
$\pi _*\mathcal {A}^\mathrm {mod}_{\widetilde U_\varepsilon \times S}$. This follows from the definition of moderate growth, owing to the properness of ![]() $\pi$.
$\pi$.
4.c Regular holonomicity of the Deligne extension of an  $S$-locally constant sheaf
$S$-locally constant sheaf
We continue to refer to Notation 4.5 and assume that ![]() $Y=D$ has normal crossings.
$Y=D$ has normal crossings.
Theorem 4.15 Assume that ![]() $L$ is a coherent
$L$ is a coherent ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$. Then:
$X^*\times S$. Then:
(i) the subsheaf
 $\widetilde E_L$ of
$\widetilde E_L$ of  $j_*E_L$ is
$j_*E_L$ is  $\mathcal {O}_{X\times S}(*D)$-coherent;
$\mathcal {O}_{X\times S}(*D)$-coherent;(ii) the functor
 $L\mapsto \widetilde E_L$ from the category of coherent
$L\mapsto \widetilde E_L$ from the category of coherent  $S$-locally constant sheaves on
$S$-locally constant sheaves on  $X^*\times S$ to that of
$X^*\times S$ to that of  $\mathcal {D}_{X\times S/S}$-modules is fully faithful;
$\mathcal {D}_{X\times S/S}$-modules is fully faithful;(iii) as a
 $\mathcal {D}_{X\times S/S}$-module,
$\mathcal {D}_{X\times S/S}$-module,  $(\widetilde E_L,\nabla )$ is regular holonomic.
$(\widetilde E_L,\nabla )$ is regular holonomic.
We make use of the following flattening result for a coherent ![]() $\mathcal {O}_S$-module (here, we only need a local version, but the corresponding global version also holds true).
$\mathcal {O}_S$-module (here, we only need a local version, but the corresponding global version also holds true).
Proposition 4.16 Near each ![]() $s_o \in S$, there exists a projective modification
$s_o \in S$, there exists a projective modification ![]() $\pi :S'\rightarrow S$ with
$\pi :S'\rightarrow S$ with ![]() $S'$ smooth such that the torsion-free quotient of
$S'$ smooth such that the torsion-free quotient of ![]() $\pi ^*G$ is
$\pi ^*G$ is ![]() $\mathcal {O}_{S'}$-locally free.
$\mathcal {O}_{S'}$-locally free.
Proof. We first apply the flattening theorem [Reference RossiRos68, Theorem 3.5] to the coherent sheaf ![]() $G$. There exists thus a projective modification
$G$. There exists thus a projective modification ![]() $\pi '':S''\rightarrow S$ such that
$\pi '':S''\rightarrow S$ such that ![]() $\pi ^{\prime \prime *}G$, when quotiented by its
$\pi ^{\prime \prime *}G$, when quotiented by its ![]() $\mathcal {O}_{S''}$-torsion, is
$\mathcal {O}_{S''}$-torsion, is ![]() $\mathcal {O}_{S''}$-locally free. We then apply resolution of singularities
$\mathcal {O}_{S''}$-locally free. We then apply resolution of singularities ![]() $\pi ':S'\rightarrow S''$ of
$\pi ':S'\rightarrow S''$ of ![]() $S''$ in the neighborhood of the projective subset
$S''$ in the neighborhood of the projective subset ![]() $\pi ^{\prime \prime -1}(s_o)$ (cf. [Reference HironakaHir64, § 7, Main Theorem I
$\pi ^{\prime \prime -1}(s_o)$ (cf. [Reference HironakaHir64, § 7, Main Theorem I![]() $'$]) and denote by
$'$]) and denote by ![]() $\pi$ the morphism
$\pi$ the morphism ![]() $\pi ''\circ \pi '$, which answers the question.
$\pi ''\circ \pi '$, which answers the question.
Proof of Theorem 4.15(i) We recall the proof of [Reference Monteiro Fernandes and SabbahMFS19, Theorem 2.6] for the ![]() $\mathcal {O}_{X\times S}(*D)$-coherence. The problem is local on
$\mathcal {O}_{X\times S}(*D)$-coherence. The problem is local on ![]() $X\times S$. We thus assume that
$X\times S$. We thus assume that ![]() $X\times S$ is a small neighborhood of
$X\times S$ is a small neighborhood of ![]() $(x_o,s_o)$ as above. In such a neighborhood, giving the local system is equivalent to giving
$(x_o,s_o)$ as above. In such a neighborhood, giving the local system is equivalent to giving ![]() $T_1,\ldots,T_\ell \in \operatorname {Aut}(G)$ which pairwise commute. Let
$T_1,\ldots,T_\ell \in \operatorname {Aut}(G)$ which pairwise commute. Let ![]() $U(s_o)$ be an open neighborhood of
$U(s_o)$ be an open neighborhood of ![]() $s_o$ isomorphic to an open polydisc. The formula [Reference WangWan08, (2.11)] defining a logarithm of
$s_o$ isomorphic to an open polydisc. The formula [Reference WangWan08, (2.11)] defining a logarithm of ![]() $T_i$ can be used to show that there exist
$T_i$ can be used to show that there exist ![]() $A_1(s),\ldots,A_\ell (s)\in \operatorname {End}_{\mathcal {O}_S}(G_{|U(s_o)})$ which pairwise commute, such that
$A_1(s),\ldots,A_\ell (s)\in \operatorname {End}_{\mathcal {O}_S}(G_{|U(s_o)})$ which pairwise commute, such that ![]() $T_i=\exp (-2\pi i A_i(s))$ for each
$T_i=\exp (-2\pi i A_i(s))$ for each ![]() $i$ on
$i$ on ![]() $U(s_o)$ (cf. [Reference WangWan08, Corollary 2.3.10 and Chapter 3]). Set
$U(s_o)$ (cf. [Reference WangWan08, Corollary 2.3.10 and Chapter 3]). Set ![]() $\widehat E_G:=\mathcal {O}_{X\times S}(*D)\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G$, equipped with the connection
$\widehat E_G:=\mathcal {O}_{X\times S}(*D)\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G$, equipped with the connection ![]() $\widehat \nabla$ such that
$\widehat \nabla$ such that ![]() $\widehat \nabla _{x_i\partial _{x_i}}$ acts on
$\widehat \nabla _{x_i\partial _{x_i}}$ acts on ![]() $1\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G$ by
$1\otimes _{p^{-1}\mathcal {O}_S}p^{-1}G$ by ![]() $\operatorname {Id}\otimes A_i(s)$ if
$\operatorname {Id}\otimes A_i(s)$ if ![]() $i=1,\ldots,\ell$, and zero otherwise. Then the monodromy representation of
$i=1,\ldots,\ell$, and zero otherwise. Then the monodromy representation of ![]() $\widehat \nabla$ on
$\widehat \nabla$ on ![]() $\widehat E_{G|X^*\times S}$ is given by
$\widehat E_{G|X^*\times S}$ is given by ![]() $T_1,\ldots,T_\ell$, hence an isomorphism
$T_1,\ldots,T_\ell$, hence an isomorphism ![]() $L\simeq (\widehat E_{G|X^*\times S})^{\widehat \nabla }$, from which one deduces, according to Corollary 4.3, an isomorphism
$L\simeq (\widehat E_{G|X^*\times S})^{\widehat \nabla }$, from which one deduces, according to Corollary 4.3, an isomorphism
 \begin{align} (E_L,\nabla)&=(\mathcal{O}_{X^*\times S}\otimes_{p^{-1}\mathcal{O}_S}L,\mathrm{d}_{X^*\times S/S}\otimes\operatorname{Id})\nonumber\\ &\simeq(\mathcal{O}_{X^*\times S}\otimes_{p^{-1}\mathcal{O}_S}(\widehat E_{G|X^*\times S})^{\widehat\nabla}, \mathrm{d}_{X^*\times S/S}\otimes\operatorname{Id})\simeq(\widehat E_{G|X^*\times S}, \widehat\nabla). \end{align}
\begin{align} (E_L,\nabla)&=(\mathcal{O}_{X^*\times S}\otimes_{p^{-1}\mathcal{O}_S}L,\mathrm{d}_{X^*\times S/S}\otimes\operatorname{Id})\nonumber\\ &\simeq(\mathcal{O}_{X^*\times S}\otimes_{p^{-1}\mathcal{O}_S}(\widehat E_{G|X^*\times S})^{\widehat\nabla}, \mathrm{d}_{X^*\times S/S}\otimes\operatorname{Id})\simeq(\widehat E_{G|X^*\times S}, \widehat\nabla). \end{align} It follows that ![]() $\widetilde E_L \simeq \widetilde {\widehat E}_{G|X^*\times S}$ and we are thus reduced to proving that
$\widetilde E_L \simeq \widetilde {\widehat E}_{G|X^*\times S}$ and we are thus reduced to proving that ![]() $\widetilde {\widehat E}_{G|X^*\times S} = \widehat E_G$ (we have trivialized the locally constant sheaf but the connection is not trivial anymore).
$\widetilde {\widehat E}_{G|X^*\times S} = \widehat E_G$ (we have trivialized the locally constant sheaf but the connection is not trivial anymore).
Remark 4.18 Let ![]() $p_{X^*}^{-1}G$ be the constant
$p_{X^*}^{-1}G$ be the constant ![]() $S$-local system on
$S$-local system on ![]() $X^*\times S$. Thus, locally on
$X^*\times S$. Thus, locally on ![]() $X\times S$, there exist
$X\times S$, there exist ![]() $\mathcal {O}_{X^*\times S}$-linear isomorphisms
$\mathcal {O}_{X^*\times S}$-linear isomorphisms ![]() $E_L\simeq \widehat E_{G|X^*\times S}\simeq E_{p_{X^*}^{-1}G},$ but, in general, we do not have
$E_L\simeq \widehat E_{G|X^*\times S}\simeq E_{p_{X^*}^{-1}G},$ but, in general, we do not have ![]() $(E_L,\nabla )\simeq (E_{p_{X^*}^{-1}G},\widehat \nabla )$, i.e., this isomorphism is not
$(E_L,\nabla )\simeq (E_{p_{X^*}^{-1}G},\widehat \nabla )$, i.e., this isomorphism is not ![]() $\mathcal {D}_{X^*\times S/S}$-linear.
$\mathcal {D}_{X^*\times S/S}$-linear.
Let us prove the inclusion ![]() $\widetilde {\widehat E}_{G|X^*\times S}\subset \widehat E_G$. Let
$\widetilde {\widehat E}_{G|X^*\times S}\subset \widehat E_G$. Let ![]() $v\in (j_*\widehat E_G)_{(x_o,s_o)}$ be locally defined on
$v\in (j_*\widehat E_G)_{(x_o,s_o)}$ be locally defined on ![]() $U\times U(s_o)$. On any polysector
$U\times U(s_o)$. On any polysector ![]() $U^*_\varepsilon \times U(s_o)$, we can choose logarithms of
$U^*_\varepsilon \times U(s_o)$, we can choose logarithms of ![]() $x_i$ (
$x_i$ (![]() $i=1,\ldots,\ell$) and the automorphism
$i=1,\ldots,\ell$) and the automorphism ![]() $\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ of
$\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ of ![]() $\widehat E_{G|X^*\times S}=\mathcal {O}_{U^*_\varepsilon \times U(s_o)}\otimes _{p^{-1}\mathcal {O}_{U(s_o)}}p^{-1}G$ is well-defined by setting
$\widehat E_{G|X^*\times S}=\mathcal {O}_{U^*_\varepsilon \times U(s_o)}\otimes _{p^{-1}\mathcal {O}_{U(s_o)}}p^{-1}G$ is well-defined by setting ![]() $x_i^{A_i(s)}=\sum _k[(\log x_i)^k/k!]\otimes A_i(s)^k$. By definition,
$x_i^{A_i(s)}=\sum _k[(\log x_i)^k/k!]\otimes A_i(s)^k$. By definition, ![]() $v$ has moderate growth, i.e., is a local section of
$v$ has moderate growth, i.e., is a local section of ![]() $\widetilde {\widehat E\,}_{G|X^*\times S}$, if and only if, on any such polysector
$\widetilde {\widehat E\,}_{G|X^*\times S}$, if and only if, on any such polysector ![]() $\widetilde U_\varepsilon \times U(s_o)$, the section
$\widetilde U_\varepsilon \times U(s_o)$, the section ![]() $w:=(\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)})\cdot v$ is a section of
$w:=(\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)})\cdot v$ is a section of ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}\otimes _{\widetilde {p}^{-1}\mathcal {O}_S}\widetilde p^{-1}G$.
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}\otimes _{\widetilde {p}^{-1}\mathcal {O}_S}\widetilde p^{-1}G$.
Let ![]() $(g_j)$ be a family of local generators of
$(g_j)$ be a family of local generators of ![]() $G$ on
$G$ on ![]() $U(s_o)$. The entries of the matrices of
$U(s_o)$. The entries of the matrices of ![]() $\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ and of
$\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ and of ![]() $\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}$ with respect to this family have moderate growth. If, on such a polysector,
$\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}$ with respect to this family have moderate growth. If, on such a polysector, ![]() $w$ writes
$w$ writes ![]() $\sum _jw_j\otimes g_j$, where
$\sum _jw_j\otimes g_j$, where ![]() $w_j$ are sections of
$w_j$ are sections of ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$, then
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$, then ![]() $v=\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}\cdot w$ writes similarly
$v=\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}\cdot w$ writes similarly ![]() $\sum _jv_j\otimes g_j$, where
$\sum _jv_j\otimes g_j$, where ![]() $v_j$ are sections of
$v_j$ are sections of ![]() $\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$. Conversely, if
$\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}$. Conversely, if ![]() $v$ has the previous expression, then so does
$v$ has the previous expression, then so does ![]() $w=\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}\cdot v$. We conclude that, for any such polysector, the moderate growth condition on
$w=\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}\cdot v$. We conclude that, for any such polysector, the moderate growth condition on ![]() $v$ is equivalent to
$v$ is equivalent to ![]() $v\in \Gamma (\widetilde U_\varepsilon \times U(s_o);\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}\otimes _{\widetilde {p}^{-1}\mathcal {O}_S}\widetilde p^{-1}G)$. In other words, if
$v\in \Gamma (\widetilde U_\varepsilon \times U(s_o);\mathcal {A}^\mathrm {mod}_{\widetilde X\times S}\otimes _{\widetilde {p}^{-1}\mathcal {O}_S}\widetilde p^{-1}G)$. In other words, if ![]() $v$ has moderate growth, we have by (4.9) that
$v$ has moderate growth, we have by (4.9) that
 \begin{align*} v\in\Gamma(U\times U(s_o);\varpi_*\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G) &=\Gamma(U\times U(s_o);\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S} p^{-1}G)\\ &=\Gamma(U\times U(s_o);\widehat E_G), \end{align*}
\begin{align*} v\in\Gamma(U\times U(s_o);\varpi_*\mathcal{A}^\mathrm{mod}_{\widetilde X\times S}\otimes_{\widetilde{p}^{-1}\mathcal{O}_S}\widetilde p^{-1}G) &=\Gamma(U\times U(s_o);\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S} p^{-1}G)\\ &=\Gamma(U\times U(s_o);\widehat E_G), \end{align*}
hence ![]() $\widetilde {\widehat E}_{G|X^*\times S}\subset \widehat E_G$. The reverse inclusion also follows from the moderate growth of the entries of the matrices of
$\widetilde {\widehat E}_{G|X^*\times S}\subset \widehat E_G$. The reverse inclusion also follows from the moderate growth of the entries of the matrices of ![]() $\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ and of
$\mathop {\textstyle \prod } _{i=1}^\ell x_i^{A_i(s)}$ and of ![]() $\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}$.
$\mathop {\textstyle \prod } _{i=1}^\ell x_i^{-A_i(s)}$.
Proof of Theorem 4.15(ii) We already know, by the Riemann–Hilbert correspondence of [Reference DeligneDel70, Theorem 2.23], that the functor ![]() $L\mapsto E_L$ is fully faithful, and it is clearly exact, so it remains to prove that
$L\mapsto E_L$ is fully faithful, and it is clearly exact, so it remains to prove that ![]() $E_L\mapsto \widetilde E_L$ is so. Faithfulness is clear. Let us check fullness. Let
$E_L\mapsto \widetilde E_L$ is so. Faithfulness is clear. Let us check fullness. Let ![]() $\varphi :\widetilde E_L\rightarrow \widetilde E_{L'}$ be a morphism and set
$\varphi :\widetilde E_L\rightarrow \widetilde E_{L'}$ be a morphism and set ![]() $\widetilde \varphi =\widetilde {j^*\varphi }:\widetilde E_L\rightarrow \widetilde E_{L'}$. The kernel and cokernel of
$\widetilde \varphi =\widetilde {j^*\varphi }:\widetilde E_L\rightarrow \widetilde E_{L'}$. The kernel and cokernel of ![]() $\varphi -\widetilde \varphi$ are coherent
$\varphi -\widetilde \varphi$ are coherent ![]() $\mathcal {O}_{X\times S}(*D)$-modules by Theorem 4.15(i), and are zero when restricted to
$\mathcal {O}_{X\times S}(*D)$-modules by Theorem 4.15(i), and are zero when restricted to ![]() $X^*\times S$. Therefore they are zero, and
$X^*\times S$. Therefore they are zero, and ![]() $\varphi =\widetilde \varphi$, proving the assertion.
$\varphi =\widetilde \varphi$, proving the assertion.
Proof of Theorem 4.15(iii) The question is local at a point ![]() $(x_o,s_o)\in X\times S$. By the proof of Theorem 4.15(i), we can work with
$(x_o,s_o)\in X\times S$. By the proof of Theorem 4.15(i), we can work with
(with ![]() $\widehat \nabla =\mathrm {d}\otimes \operatorname {Id}+\sum _i\mathrm {d} x_i/x_i\otimes A_i$ and
$\widehat \nabla =\mathrm {d}\otimes \operatorname {Id}+\sum _i\mathrm {d} x_i/x_i\otimes A_i$ and ![]() $A_i\in \operatorname {End}_{\mathcal {O}_S}(G)$). Our method is to reduce to the case where
$A_i\in \operatorname {End}_{\mathcal {O}_S}(G)$). Our method is to reduce to the case where ![]() $G$ is locally free of rank one and then prove Theorem 4.15(iii) for it.
$G$ is locally free of rank one and then prove Theorem 4.15(iii) for it.
We argue by induction on the lexicographically ordered pair ![]() $(\dim S,\operatorname {rk} G)$, where
$(\dim S,\operatorname {rk} G)$, where ![]() $\operatorname {rk} G$ is the rank of
$\operatorname {rk} G$ is the rank of ![]() $G$ at a general point of
$G$ at a general point of ![]() $S$. The case
$S$. The case ![]() $\dim S=0$ and
$\dim S=0$ and ![]() $\operatorname {rk} G$ arbitrary is well-known. We thus assume that
$\operatorname {rk} G$ arbitrary is well-known. We thus assume that ![]() $d=\dim S\geqslant 1$ and
$d=\dim S\geqslant 1$ and ![]() $r=\operatorname {rk} G\geqslant 0$, and that Theorem 4.15(iii) holds for
$r=\operatorname {rk} G\geqslant 0$, and that Theorem 4.15(iii) holds for ![]() $(\widehat E_{G'},\widehat \nabla )$ for any
$(\widehat E_{G'},\widehat \nabla )$ for any ![]() $p^{\prime -1}\mathcal {O}_{S'}$-module
$p^{\prime -1}\mathcal {O}_{S'}$-module ![]() $G'$ with
$G'$ with ![]() $(\dim S',\operatorname {rk} G')<(d,r)$.
$(\dim S',\operatorname {rk} G')<(d,r)$.
Step 1: the case ![]() $(d,0)$. If
$(d,0)$. If ![]() $\operatorname {rk} G=0$,
$\operatorname {rk} G=0$, ![]() $G$ is an
$G$ is an ![]() $\mathcal {O}_S$-torsion module. As the question is local, we can assume that the support of
$\mathcal {O}_S$-torsion module. As the question is local, we can assume that the support of ![]() $G$ is contained in a hypersurface
$G$ is contained in a hypersurface ![]() $T\subset S$ locally presented as in the local Setting 3.12. Then
$T\subset S$ locally presented as in the local Setting 3.12. Then ![]() $G$ is
$G$ is ![]() $q^{-1}\mathcal {O}_{S'}$-coherent and is endowed with an endomorphism
$q^{-1}\mathcal {O}_{S'}$-coherent and is endowed with an endomorphism ![]() $t$ (i.e., multiplication by
$t$ (i.e., multiplication by ![]() $t$), so that the natural
$t$), so that the natural ![]() $\mathcal {O}_S$-linear morphism
$\mathcal {O}_S$-linear morphism ![]() $\mathcal {O}_S\otimes _{q^{-1}\mathcal {O}_{S'}[t]}G\rightarrow G$ is an isomorphism. Furthermore, the endomorphisms
$\mathcal {O}_S\otimes _{q^{-1}\mathcal {O}_{S'}[t]}G\rightarrow G$ is an isomorphism. Furthermore, the endomorphisms ![]() $A_i$ are
$A_i$ are ![]() $q^{-1}\mathcal {O}_{S'}$-linear (via the natural inclusion
$q^{-1}\mathcal {O}_{S'}$-linear (via the natural inclusion ![]() $q^{-1}\mathcal {O}_{S'}\mathrel {\hookrightarrow}\mathcal {O}_S$. Let us set
$q^{-1}\mathcal {O}_{S'}\mathrel {\hookrightarrow}\mathcal {O}_S$. Let us set ![]() $(\widehat E'_G,\nabla )=(\widehat E_G,\widehat \nabla )$ when regarded as a
$(\widehat E'_G,\nabla )=(\widehat E_G,\widehat \nabla )$ when regarded as a ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-module. By the induction hypothesis, it is regular holonomic. By Corollary 3.14, we conclude that
$q^{-1}\mathcal {D}_{X\times S'/S'}$-module. By the induction hypothesis, it is regular holonomic. By Corollary 3.14, we conclude that ![]() $(\widehat E_G,\widehat \nabla )$ is regular holonomic, so that Theorem 4.15(iii) holds for
$(\widehat E_G,\widehat \nabla )$ is regular holonomic, so that Theorem 4.15(iii) holds for ![]() $(\widehat E_G,\widehat \nabla )$.
$(\widehat E_G,\widehat \nabla )$.
Step 2: reduction after proper surjective generically finite base change. Let ![]() $\pi \,{:}\,S' \rightarrow S$ be a proper surjective generically finite morphism of complex manifolds and let
$\pi \,{:}\,S' \rightarrow S$ be a proper surjective generically finite morphism of complex manifolds and let ![]() $p':X\times S'\rightarrow S'$ denote the projection. Let us assume that Theorem 4.15(iii) holds for
$p':X\times S'\rightarrow S'$ denote the projection. Let us assume that Theorem 4.15(iii) holds for ![]() $(\mathcal {O}_{X\times S'}(*D)\otimes _{p^{\prime -1}\mathcal {O}_{S'}} p^{\prime -1}\pi ^*G,\pi ^*\widehat \nabla )$. The purpose of step 2 is to show that, under such an assumption, Theorem 4.15(iii) holds for
$(\mathcal {O}_{X\times S'}(*D)\otimes _{p^{\prime -1}\mathcal {O}_{S'}} p^{\prime -1}\pi ^*G,\pi ^*\widehat \nabla )$. The purpose of step 2 is to show that, under such an assumption, Theorem 4.15(iii) holds for ![]() $(\widehat E_G,\widehat \nabla )$.
$(\widehat E_G,\widehat \nabla )$.
From now on, we assume ![]() $\dim S=d$ and
$\dim S=d$ and ![]() $\operatorname {rk} G\geqslant 1$. Let
$\operatorname {rk} G\geqslant 1$. Let ![]() $G'$ be the
$G'$ be the ![]() $\mathcal {O}_S$-torsion subsheaf of
$\mathcal {O}_S$-torsion subsheaf of ![]() $G$. We note that the endomorphisms
$G$. We note that the endomorphisms ![]() $A_i$ of
$A_i$ of ![]() $G$ preserve
$G$ preserve ![]() $G'$, so the exact sequence
$G'$, so the exact sequence ![]() $0\rightarrow G'\rightarrow G\rightarrow G''\to 0$ with
$0\rightarrow G'\rightarrow G\rightarrow G''\to 0$ with ![]() $G''$ being torsion-free gives rise to an exact sequence
$G''$ being torsion-free gives rise to an exact sequence
As Theorem 4.15(iii) holds for ![]() $(\widehat E_{G'},\widehat \nabla )$ by step 1, it is enough to prove Theorem 4.15(iii) for
$(\widehat E_{G'},\widehat \nabla )$ by step 1, it is enough to prove Theorem 4.15(iii) for ![]() $(\widehat E_{G''},\widehat \nabla )$. In other words, we may assume that
$(\widehat E_{G''},\widehat \nabla )$. In other words, we may assume that ![]() $G$ is torsion-free.
$G$ is torsion-free.
By assumption, there exists a closed analytic subset ![]() $T$ of codimension
$T$ of codimension ![]() $\geqslant 1$ in
$\geqslant 1$ in ![]() $S$ such that, setting
$S$ such that, setting ![]() $T'=\pi ^{-1}(T)$, the morphism
$T'=\pi ^{-1}(T)$, the morphism ![]() $\pi :S'\smallsetminus T'\rightarrow S\smallsetminus T$ is finite étale. We have
$\pi :S'\smallsetminus T'\rightarrow S\smallsetminus T$ is finite étale. We have ![]() $\dim S'=\dim S$ and
$\dim S'=\dim S$ and ![]() $\dim T'<\dim S$.
$\dim T'<\dim S$.
Remark that we have, for any holomorphic map ![]() $\pi :S'\rightarrow S$, and denoting for clarity by
$\pi :S'\rightarrow S$, and denoting for clarity by ![]() $\widetilde \pi$ the map
$\widetilde \pi$ the map ![]() $\operatorname {Id}\times \pi :X\times S'\to X\times S$, the following list of canonical isomorphisms:
$\operatorname {Id}\times \pi :X\times S'\to X\times S$, the following list of canonical isomorphisms:
 \begin{align} &L\widetilde\pi^*\Big(\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G\Big)\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{\widetilde\pi^{-1}\mathcal{O}_{X\times S}(*D)} \widetilde\pi^{-1}\Big(\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G\Big)\nonumber\\ &\quad \overset{(*)}=\mathcal{O}_{X\times S'}(*D)\otimes^L_{\widetilde\pi^{-1}p^{-1}\mathcal{O}_S} \widetilde\pi^{-1}p^{-1}G\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{p^{\prime-1}\mathcal{O}_{S'}} \Big(p^{\prime-1}\mathcal{O}_{S'}\otimes^L_{\widetilde\pi^{-1}p^{-1}\mathcal{O}_S}\widetilde\pi^{-1}p^{-1}G\Big)\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{p^{\prime-1}\mathcal{O}_{S'}}p^{\prime-1}L\pi^*G= \mathcal{O}_{X\times S'}(*D)\otimes_{p^{\prime-1}\mathcal{O}_{S'}}p^{\prime-1}L\pi^*G, \end{align}
\begin{align} &L\widetilde\pi^*\Big(\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G\Big)\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{\widetilde\pi^{-1}\mathcal{O}_{X\times S}(*D)} \widetilde\pi^{-1}\Big(\mathcal{O}_{X\times S}(*D)\otimes_{p^{-1}\mathcal{O}_S}p^{-1}G\Big)\nonumber\\ &\quad \overset{(*)}=\mathcal{O}_{X\times S'}(*D)\otimes^L_{\widetilde\pi^{-1}p^{-1}\mathcal{O}_S} \widetilde\pi^{-1}p^{-1}G\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{p^{\prime-1}\mathcal{O}_{S'}} \Big(p^{\prime-1}\mathcal{O}_{S'}\otimes^L_{\widetilde\pi^{-1}p^{-1}\mathcal{O}_S}\widetilde\pi^{-1}p^{-1}G\Big)\nonumber\\ &\quad =\mathcal{O}_{X\times S'}(*D)\otimes^L_{p^{\prime-1}\mathcal{O}_{S'}}p^{\prime-1}L\pi^*G= \mathcal{O}_{X\times S'}(*D)\otimes_{p^{\prime-1}\mathcal{O}_{S'}}p^{\prime-1}L\pi^*G, \end{align}which reads
We conclude that, for each ![]() $j$, we have
$j$, we have ![]() $L^j\pi ^*\widehat \nabla _{x_k\partial _{x_k}}=\mathrm {d}\otimes \operatorname {Id}+\operatorname {Id}\otimes L^j\pi ^*A_k$.
$L^j\pi ^*\widehat \nabla _{x_k\partial _{x_k}}=\mathrm {d}\otimes \operatorname {Id}+\operatorname {Id}\otimes L^j\pi ^*A_k$.
Furthermore, under the assumption on ![]() $\pi$ for this step, according to the projection formula for
$\pi$ for this step, according to the projection formula for ![]() $R\widetilde \pi _*$ applied to
$R\widetilde \pi _*$ applied to ![]() $(*)$, we have
$(*)$, we have
By induction, if ![]() $j\neq 0$, Theorem 4.15(iii) holds for
$j\neq 0$, Theorem 4.15(iii) holds for ![]() $(\mathcal {O}_{X\times S'}(*D)\otimes _{p^{\prime -1}\mathcal {O}_{S'}} p^{\prime -1}L^j\pi ^*G,L^j\pi ^*\widehat \nabla )$, according to the argument given in step 1, because
$(\mathcal {O}_{X\times S'}(*D)\otimes _{p^{\prime -1}\mathcal {O}_{S'}} p^{\prime -1}L^j\pi ^*G,L^j\pi ^*\widehat \nabla )$, according to the argument given in step 1, because ![]() $L^j\pi ^*G$ is supported on
$L^j\pi ^*G$ is supported on ![]() $T'$, hence is a torsion module. Thus, Theorem 4.15(iii) holds for
$T'$, hence is a torsion module. Thus, Theorem 4.15(iii) holds for ![]() $L\pi ^*\widehat E_G$ (i.e., for each of its cohomology modules
$L\pi ^*\widehat E_G$ (i.e., for each of its cohomology modules ![]() $L^j\pi ^*\widehat E_G$) because for
$L^j\pi ^*\widehat E_G$) because for ![]() $j=0$ it is the initial assumption.
$j=0$ it is the initial assumption.
As ![]() $\widehat E_G$ is
$\widehat E_G$ is ![]() $\mathcal {O}$-quasi-coherent (cf. Remark 2.5(i)), one deduces from Lemma 2.13 that each
$\mathcal {O}$-quasi-coherent (cf. Remark 2.5(i)), one deduces from Lemma 2.13 that each ![]() $L^j\pi ^*\widehat E_G$ is
$L^j\pi ^*\widehat E_G$ is ![]() $\pi$-good. Then, by Theorem 3.15, Theorem 4.15(iii) holds for
$\pi$-good. Then, by Theorem 3.15, Theorem 4.15(iii) holds for ![]() $R\pi _*(L\pi ^*\widehat E_G)$, hence for
$R\pi _*(L\pi ^*\widehat E_G)$, hence for ![]() $\mathcal {H}^0(R\pi _*(L\pi ^*\widehat E_G))$.
$\mathcal {H}^0(R\pi _*(L\pi ^*\widehat E_G))$.
The natural morphism ![]() $\mathcal {O}_{X\times S}(*D)\rightarrow R\pi _*\mathcal {O}_{X\times S'}(*D)$ yields a morphism
$\mathcal {O}_{X\times S}(*D)\rightarrow R\pi _*\mathcal {O}_{X\times S'}(*D)$ yields a morphism
Both modules are ![]() $\mathcal {O}_{X\times S}(*D)$-coherent, hence so is the kernel of this morphism.
$\mathcal {O}_{X\times S}(*D)$-coherent, hence so is the kernel of this morphism.
On ![]() $S\smallsetminus T$, we claim that this morphism is injective: indeed, since
$S\smallsetminus T$, we claim that this morphism is injective: indeed, since ![]() $\pi :S'\smallsetminus T'\rightarrow S\smallsetminus T$ is finite étale, the trace morphism
$\pi :S'\smallsetminus T'\rightarrow S\smallsetminus T$ is finite étale, the trace morphism ![]() $\mathrm {tr}_\pi :\pi _*\mathcal {O}_{S'\smallsetminus T'}\rightarrow \mathcal {O}_{S\smallsetminus T}$ defined by
$\mathrm {tr}_\pi :\pi _*\mathcal {O}_{S'\smallsetminus T'}\rightarrow \mathcal {O}_{S\smallsetminus T}$ defined by ![]() $\mathrm {tr}_\pi (\varphi )(s)=(1/\deg \pi ) \sum _{s'\in \pi ^{-1}(s)}\varphi (s')$ satisfies
$\mathrm {tr}_\pi (\varphi )(s)=(1/\deg \pi ) \sum _{s'\in \pi ^{-1}(s)}\varphi (s')$ satisfies ![]() $\mathrm {tr}_\pi \circ \iota =\operatorname {Id}$, if
$\mathrm {tr}_\pi \circ \iota =\operatorname {Id}$, if ![]() $\iota$ denotes the natural morphism
$\iota$ denotes the natural morphism ![]() $\mathcal {O}_{S\smallsetminus T}\rightarrow \pi _*\mathcal {O}_{S'\smallsetminus T'}$; hence
$\mathcal {O}_{S\smallsetminus T}\rightarrow \pi _*\mathcal {O}_{S'\smallsetminus T'}$; hence ![]() $\widehat E_{G|S\smallsetminus T}$ is locally a direct summand of the right-hand side. As
$\widehat E_{G|S\smallsetminus T}$ is locally a direct summand of the right-hand side. As ![]() $G$, hence
$G$, hence ![]() $\widehat E_G$, is assumed to be
$\widehat E_G$, is assumed to be ![]() $\mathcal {O}_S$-torsion-free, the kernel is
$\mathcal {O}_S$-torsion-free, the kernel is ![]() $\mathcal {O}_S$-torsion-free,
$\mathcal {O}_S$-torsion-free, ![]() $\mathcal {O}_{X\times S}(*D)$-coherent and
$\mathcal {O}_{X\times S}(*D)$-coherent and ![]() $S$-supported on
$S$-supported on ![]() $T$. It is thus zero and this morphism is injective.
$T$. It is thus zero and this morphism is injective.
Furthermore, ![]() $\widehat E_G$ is
$\widehat E_G$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent: indeed, as Theorem 4.15(iii) holds for
$\mathcal {D}_{X\times S/S}$-coherent: indeed, as Theorem 4.15(iii) holds for ![]() ${\mathcal {H}^0(R\pi _*(L\pi ^* \widehat E_G))}$ and
${\mathcal {H}^0(R\pi _*(L\pi ^* \widehat E_G))}$ and ![]() $\widehat E_G$ is
$\widehat E_G$ is ![]() $\mathcal {O}$-good, it follows that
$\mathcal {O}$-good, it follows that ![]() $\widehat E_G$ is
$\widehat E_G$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent, and then regular holonomic by Proposition 3.2(iii), so that Theorem 4.15(iii) holds for
$\mathcal {D}_{X\times S/S}$-coherent, and then regular holonomic by Proposition 3.2(iii), so that Theorem 4.15(iii) holds for ![]() $\widehat E_G$.
$\widehat E_G$.
Step 3: reduction to the case where ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free. We choose
$\mathcal {O}_S$-locally free. We choose ![]() $\pi$ as in Proposition 4.16 and by step 2 we can assume from the start that the torsion-free quotient
$\pi$ as in Proposition 4.16 and by step 2 we can assume from the start that the torsion-free quotient ![]() $G''$ of
$G''$ of ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free. By step 1, it is enough to prove Theorem 4.15(iii) for
$\mathcal {O}_S$-locally free. By step 1, it is enough to prove Theorem 4.15(iii) for ![]() $(\widehat E_{G''},\widehat \nabla )$, i.e., we can assume (and we do assume from now on) that
$(\widehat E_{G''},\widehat \nabla )$, i.e., we can assume (and we do assume from now on) that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free.
$\mathcal {O}_S$-locally free.
Step 4: the case where ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free. We still work locally on
$\mathcal {O}_S$-locally free. We still work locally on ![]() $S$ and we assume that
$S$ and we assume that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-free of rank
$\mathcal {O}_S$-free of rank ![]() $r\geqslant 1$. By the induction hypothesis, Theorem 4.15(iii) holds for any
$r\geqslant 1$. By the induction hypothesis, Theorem 4.15(iii) holds for any ![]() $(\widehat E_{G'},\widehat \nabla )$ with
$(\widehat E_{G'},\widehat \nabla )$ with ![]() $\operatorname {rk} G'< r$. Locally let us fix an
$\operatorname {rk} G'< r$. Locally let us fix an ![]() $\mathcal {O}_S$-basis of
$\mathcal {O}_S$-basis of ![]() $G$ and let
$G$ and let ![]() $\mathsf {A}_1(s)$ denote the matrix of
$\mathsf {A}_1(s)$ denote the matrix of ![]() $A_1$ in this basis. Let
$A_1$ in this basis. Let ![]() $\Sigma \subset S\times \mathbb {C}$ be the zero locus of
$\Sigma \subset S\times \mathbb {C}$ be the zero locus of ![]() $P:=\det (\alpha _1\operatorname {Id}-\mathsf {A}_1)$ and let
$P:=\det (\alpha _1\operatorname {Id}-\mathsf {A}_1)$ and let ![]() $\sigma :\Sigma \rightarrow S$ denote the projection. As
$\sigma :\Sigma \rightarrow S$ denote the projection. As ![]() $P$ is a Weierstrass polynomial with respect to the variable
$P$ is a Weierstrass polynomial with respect to the variable ![]() $\alpha _1$ (considered as a coordinate on
$\alpha _1$ (considered as a coordinate on ![]() $\mathbb {C}$) with coefficients in
$\mathbb {C}$) with coefficients in ![]() $\mathcal {O}_S$,
$\mathcal {O}_S$, ![]() $\sigma$ is a finite morphism of degree
$\sigma$ is a finite morphism of degree ![]() $\deg \sigma$ and
$\deg \sigma$ and ![]() $\Sigma$ is defined by the corresponding reduced Weierstrass polynomial. We note the following two properties related to
$\Sigma$ is defined by the corresponding reduced Weierstrass polynomial. We note the following two properties related to ![]() $\sigma$ and similarly to
$\sigma$ and similarly to ![]() $\operatorname {Id}_X\times \sigma$.
$\operatorname {Id}_X\times \sigma$.
(4.21) The sheaf
 $\sigma _*\mathcal {O}_\Sigma$ is
$\sigma _*\mathcal {O}_\Sigma$ is  $\mathcal {O}_S$-free of degree
$\mathcal {O}_S$-free of degree  $\deg \sigma$ (with basis
$\deg \sigma$ (with basis  $1,\alpha _1,\ldots,\alpha _1^{\deg \sigma -1}$).
$1,\alpha _1,\ldots,\alpha _1^{\deg \sigma -1}$).(4.22) There exist dense analytic open subsets
 $\Sigma ^\circ \subset \Sigma$ and
$\Sigma ^\circ \subset \Sigma$ and  $S^\circ \subset S$ such that
$S^\circ \subset S$ such that  $\sigma :\Sigma ^\circ \rightarrow S^\circ$ is a finite covering of degree
$\sigma :\Sigma ^\circ \rightarrow S^\circ$ is a finite covering of degree  $\deg \sigma$. The corresponding trace morphism
$\deg \sigma$. The corresponding trace morphism  $\mathrm {tr}_\sigma :\sigma _*\mathcal {O}_{\Sigma ^\circ }\rightarrow \mathcal {O}_{S^\circ }$ has been defined previously. If
$\mathrm {tr}_\sigma :\sigma _*\mathcal {O}_{\Sigma ^\circ }\rightarrow \mathcal {O}_{S^\circ }$ has been defined previously. If  $\varphi$ is a section of
$\varphi$ is a section of  $\sigma _*\mathcal {O}_{\Sigma }$, its trace on
$\sigma _*\mathcal {O}_{\Sigma }$, its trace on  $\Sigma ^\circ$ is bounded on
$\Sigma ^\circ$ is bounded on  $S^\circ$, hence extends holomorphically to
$S^\circ$, hence extends holomorphically to  $S$, so that
$S$, so that  $\mathrm {tr}_\sigma$ extends as a morphism
$\mathrm {tr}_\sigma$ extends as a morphism  $\sigma _*\mathcal {O}_{\Sigma }\rightarrow \mathcal {O}_S$. If
$\sigma _*\mathcal {O}_{\Sigma }\rightarrow \mathcal {O}_S$. If  $\iota$ denotes the natural morphism
$\iota$ denotes the natural morphism  $\mathcal {O}_S\rightarrow \sigma _*\mathcal {O}_\Sigma$, we clearly have
$\mathcal {O}_S\rightarrow \sigma _*\mathcal {O}_\Sigma$, we clearly have  $\mathrm {tr}_\sigma \circ \iota =\operatorname {Id}$, making
$\mathrm {tr}_\sigma \circ \iota =\operatorname {Id}$, making  $\mathcal {O}_S$ a direct summand of
$\mathcal {O}_S$ a direct summand of  $\sigma _*\mathcal {O}_{\Sigma }$.
$\sigma _*\mathcal {O}_{\Sigma }$.
Let ![]() $\pi :S'\rightarrow \Sigma$ be a resolution of singularities of
$\pi :S'\rightarrow \Sigma$ be a resolution of singularities of ![]() $\Sigma$, so that the natural composed map
$\Sigma$, so that the natural composed map ![]() $(\sigma \circ \pi ):S'\rightarrow S$ is projective and generically finite. Let us set
$(\sigma \circ \pi ):S'\rightarrow S$ is projective and generically finite. Let us set ![]() $G'=\ker (\alpha _1\operatorname {Id}-\mathsf {A}_1\circ \sigma \circ \pi )\subset (\sigma \circ \pi )^*G$, where we regard
$G'=\ker (\alpha _1\operatorname {Id}-\mathsf {A}_1\circ \sigma \circ \pi )\subset (\sigma \circ \pi )^*G$, where we regard ![]() $\alpha _1$ as a function
$\alpha _1$ as a function ![]() $S'\rightarrow \mathbb {C}$. Noting that
$S'\rightarrow \mathbb {C}$. Noting that ![]() $\sigma \circ \pi$ is generically a local isomorphism, it follows by construction that
$\sigma \circ \pi$ is generically a local isomorphism, it follows by construction that ![]() $\operatorname {rk} G'\geqslant 1$. We consider the exact sequence
$\operatorname {rk} G'\geqslant 1$. We consider the exact sequence ![]() $0\rightarrow G'\rightarrow (\sigma \circ \pi )^*G\rightarrow G''\to 0$ which satisfies
$0\rightarrow G'\rightarrow (\sigma \circ \pi )^*G\rightarrow G''\to 0$ which satisfies ![]() $0<\operatorname {rk} G'$ and
$0<\operatorname {rk} G'$ and ![]() $\operatorname {rk} G''<\operatorname {rk} G$, and which is preserved by the endomorphisms
$\operatorname {rk} G''<\operatorname {rk} G$, and which is preserved by the endomorphisms ![]() $(\sigma \circ \pi )^*A_i$, so that it induces an exact sequence of
$(\sigma \circ \pi )^*A_i$, so that it induces an exact sequence of ![]() $\mathcal {D}_{X\times S/S}$-modules:
$\mathcal {D}_{X\times S/S}$-modules:
If ![]() $\operatorname {rk} G'<\operatorname {rk} G$, we can apply induction to
$\operatorname {rk} G'<\operatorname {rk} G$, we can apply induction to ![]() $(\widehat E_{G'},\widehat \nabla ),(\widehat E_{G''},\widehat \nabla )$ and conclude that Theorem 4.15(iii) holds for
$(\widehat E_{G'},\widehat \nabla ),(\widehat E_{G''},\widehat \nabla )$ and conclude that Theorem 4.15(iii) holds for ![]() $(\sigma \circ \pi )^*(\widehat E_G,\widehat \nabla )$, hence for
$(\sigma \circ \pi )^*(\widehat E_G,\widehat \nabla )$, hence for ![]() $(\widehat E_G,\widehat \nabla )$ according to step 2.
$(\widehat E_G,\widehat \nabla )$ according to step 2.
If ![]() $\operatorname {rk} G'=\operatorname {rk} G$, then
$\operatorname {rk} G'=\operatorname {rk} G$, then ![]() $\operatorname {rk} G''=0$, so step 1 applies to
$\operatorname {rk} G''=0$, so step 1 applies to ![]() $(\widehat E_{G''},\widehat \nabla )$, and we are reduced to proving Theorem 4.15(iii) for
$(\widehat E_{G''},\widehat \nabla )$, and we are reduced to proving Theorem 4.15(iii) for ![]() $(\widehat E_{G'},\widehat \nabla )$, i.e., we can assume that
$(\widehat E_{G'},\widehat \nabla )$, i.e., we can assume that ![]() $A_1=\alpha _1\operatorname {Id}$. Iterating the argument, we are reduced to the case where
$A_1=\alpha _1\operatorname {Id}$. Iterating the argument, we are reduced to the case where ![]() $A_i=\alpha _i\operatorname {Id}$ for
$A_i=\alpha _i\operatorname {Id}$ for ![]() $i=1,\ldots,\ell$, where
$i=1,\ldots,\ell$, where ![]() $\alpha _1,\ldots,\alpha _\ell$ are holomorphic functions on
$\alpha _1,\ldots,\alpha _\ell$ are holomorphic functions on ![]() $S$, and
$S$, and ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free. By considering a local basis of
$\mathcal {O}_S$-locally free. By considering a local basis of ![]() $G$, it suffices to consider the case where
$G$, it suffices to consider the case where ![]() $\operatorname {rk} G=1$.
$\operatorname {rk} G=1$.
Step 5: the case where ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free of rank one. We now consider
$\mathcal {O}_S$-locally free of rank one. We now consider ![]() $(\widehat E_G,\widehat \nabla )=(\mathcal {O}_{X\times S}(*D),\mathrm {d}_{X\times S/S}+\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i)$. The argument for obtaining Theorem 4.15(iii) is then similar to that used in the proof of [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.8]. One can assume that, in the neighborhood of
$(\widehat E_G,\widehat \nabla )=(\mathcal {O}_{X\times S}(*D),\mathrm {d}_{X\times S/S}+\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i)$. The argument for obtaining Theorem 4.15(iii) is then similar to that used in the proof of [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.8]. One can assume that, in the neighborhood of ![]() $s_o$ and for any
$s_o$ and for any ![]() $i$,
$i$, ![]() $\alpha _i(s)\in \mathbb {Z}\Rightarrow \alpha _i(s)=0$. Then there exists a surjective morphism
$\alpha _i(s)\in \mathbb {Z}\Rightarrow \alpha _i(s)=0$. Then there exists a surjective morphism
sending ![]() $1$ to
$1$ to ![]() $1/x_1\cdots x_\ell$, which is easily seen to be an isomorphism by the condition on
$1/x_1\cdots x_\ell$, which is easily seen to be an isomorphism by the condition on ![]() $(\alpha _i)_{i=1,\ldots,\ell }$.
$(\alpha _i)_{i=1,\ldots,\ell }$.
Proof of Proposition 4.13(iii) The statement is local, so, as a consequence of (4.17) in the proof of Theorem 4.15(i) and keeping the same notation, we are reduced to proving ![]() $\pi ^*(\widehat E_G,\widehat \nabla )\simeq (\widehat E_{\pi ^*G},\widehat \nabla )$, that is,
$\pi ^*(\widehat E_G,\widehat \nabla )\simeq (\widehat E_{\pi ^*G},\widehat \nabla )$, that is,
which follows by taking the ![]() $0$-cohomology in (4.19).
$0$-cohomology in (4.19).
4.d  $\mathcal {D}_{X\times S/S}$-modules of D-type
$\mathcal {D}_{X\times S/S}$-modules of D-type
Recall Notation 4.5. In this section, we exhibit a family of regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules, that we call of D-type and we prove in Proposition 4.26 a special case of the analogue in the relative setting of [Reference Kashiwara and KawaiKK81, Theorem 2.3.2] asserting that the restriction functor to the complement of the divisor is an equivalence of categories. The general case will be obtained in Theorem 6.17.
$\mathcal {D}_{X\times S/S}$-modules, that we call of D-type and we prove in Proposition 4.26 a special case of the analogue in the relative setting of [Reference Kashiwara and KawaiKK81, Theorem 2.3.2] asserting that the restriction functor to the complement of the divisor is an equivalence of categories. The general case will be obtained in Theorem 6.17.
Let ![]() $Y$ be a closed hypersurface of
$Y$ be a closed hypersurface of ![]() $X$.
$X$.
Definition 4.23 We say that a coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module
$\mathcal {D}_{X\times S/S}(*Y)$-module ![]() $\mathcal {L}$ is of D-type if:
$\mathcal {L}$ is of D-type if:
(a) there exists a coherent
 $S$-locally constant sheaf
$S$-locally constant sheaf  $L$ on
$L$ on  $X^*\times S$ such that
$X^*\times S$ such that  $\mathcal {L}_{|X^*\times S}\simeq E_L=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$, equivalently,
$\mathcal {L}_{|X^*\times S}\simeq E_L=(\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X^*\times S/S}\otimes \operatorname {Id})$, equivalently,  $\mathcal {L}_{|X^*\times S}$ is
$\mathcal {L}_{|X^*\times S}$ is  $\mathcal {D}_{X^*\times S/S}$-holonomic with characteristic variety contained in the zero section;
$\mathcal {D}_{X^*\times S/S}$-holonomic with characteristic variety contained in the zero section;(b) for each
 $s\in S$, the cohomology of
$s\in S$, the cohomology of  $Li_s^*\mathcal {L}$ is
$Li_s^*\mathcal {L}$ is  $\mathcal {D}_{X}$-regular holonomic (in particular,
$\mathcal {D}_{X}$-regular holonomic (in particular,  $\mathcal {D}_{X}$-coherent); in other words,
$\mathcal {D}_{X}$-coherent); in other words,  $\mathcal {L}$ satisfies condition
$\mathcal {L}$ satisfies condition  $(\mathrm {Reg}\,2)$ and, thus, condition
$(\mathrm {Reg}\,2)$ and, thus, condition  $(\mathrm {Reg}\,1)$ (cf. Proposition 3.2).
$(\mathrm {Reg}\,1)$ (cf. Proposition 3.2).
We say that ![]() $\mathcal {L}$ is strict if
$\mathcal {L}$ is strict if ![]() $L$ is
$L$ is ![]() $p^{-1}\mathcal {O}_S$-locally free.
$p^{-1}\mathcal {O}_S$-locally free.
We denote by ![]() $\mathrm {Mod}_Y(\mathcal {D}_{X\times S/S}(*Y))$ the full subcategory of
$\mathrm {Mod}_Y(\mathcal {D}_{X\times S/S}(*Y))$ the full subcategory of ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$ whose objects are coherent
$\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$ whose objects are coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-modules of D-type.
$\mathcal {D}_{X\times S/S}(*Y)$-modules of D-type.
Lemma 4.24 For ![]() $\pi :S'\rightarrow S$ and
$\pi :S'\rightarrow S$ and ![]() $\mathcal {L}\in \mathrm {Mod}_Y(\mathcal {D}_{X\times S/S}(*Y))$,
$\mathcal {L}\in \mathrm {Mod}_Y(\mathcal {D}_{X\times S/S}(*Y))$, ![]() $L\pi ^*\mathcal {L}$ has cohomology in
$L\pi ^*\mathcal {L}$ has cohomology in ![]() $\mathrm {Mod}_Y(\mathcal {D}_{X\times S'/S'}(*Y))$.
$\mathrm {Mod}_Y(\mathcal {D}_{X\times S'/S'}(*Y))$.
Proof. The good behavior of Definition 4.23(a) by base pullback is clear. Let us check that of Definition 4.23(b). Arguing as in Lemma 2.14, we see that ![]() $L\pi ^*\mathcal {L}$ is an object of
$L\pi ^*\mathcal {L}$ is an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S'/S'}(*D))$. For any
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {D}_{X\times S'/S'}(*D))$. For any ![]() $s'\in S'$ we have
$s'\in S'$ we have ![]() $Li_{s'}^*L\pi ^*\mathcal {L}\simeq Li_{\pi (s')}^*\mathcal {L}$, so the complex
$Li_{s'}^*L\pi ^*\mathcal {L}\simeq Li_{\pi (s')}^*\mathcal {L}$, so the complex ![]() $Li_{s'}^*L\pi ^*\mathcal {L}$ has
$Li_{s'}^*L\pi ^*\mathcal {L}$ has ![]() $\mathcal {D}_{X}$-regular holonomic cohomology. By Proposition 3.2(i), each
$\mathcal {D}_{X}$-regular holonomic cohomology. By Proposition 3.2(i), each ![]() $Li_{s'}^*L^j\pi ^*\mathcal {L}$ also has
$Li_{s'}^*L^j\pi ^*\mathcal {L}$ also has ![]() $\mathcal {D}_{X}$-regular holonomic cohomology.
$\mathcal {D}_{X}$-regular holonomic cohomology.
Proposition 4.25 Assume that ![]() $Y=D$ is a divisor with normal crossings in
$Y=D$ is a divisor with normal crossings in ![]() $X$.
$X$.
(i) If
 $\mathcal {L}$ is
$\mathcal {L}$ is  $\mathcal {D}_{X\times S/S}(*D)$-coherent of D-type and strict, then the natural morphism
$\mathcal {D}_{X\times S/S}(*D)$-coherent of D-type and strict, then the natural morphism  $\psi :\mathcal {L}\rightarrow j_*E_L$ sends
$\psi :\mathcal {L}\rightarrow j_*E_L$ sends  $\mathcal {L}$ isomorphically to
$\mathcal {L}$ isomorphically to  $\widetilde E_L$.
$\widetilde E_L$.(ii) If
 $\mathcal {L}$ is
$\mathcal {L}$ is  $\mathcal {D}_{X\times S/S}(*D)$-coherent of D-type, then
$\mathcal {D}_{X\times S/S}(*D)$-coherent of D-type, then  $\mathcal {L}$ is
$\mathcal {L}$ is  $\mathcal {D}_{X\times S/S}$-regular holonomic.
$\mathcal {D}_{X\times S/S}$-regular holonomic.
Proof. We note that the question is local on ![]() $X\times S$, so we may replace
$X\times S$, so we may replace ![]() $E_L$ with
$E_L$ with ![]() $\widehat E_{G|X^*\times S}$ as in (4.17). Namely, we have
$\widehat E_{G|X^*\times S}$ as in (4.17). Namely, we have
We note the following.
• If
 $\mathcal {L}$ is strict, the second assertion follows from the first one, because
$\mathcal {L}$ is strict, the second assertion follows from the first one, because  $\widetilde E_L$ is
$\widetilde E_L$ is  $\mathcal {D}_{X\times S/S}$-regular holonomic (Theorem 4.15(iii)).
$\mathcal {D}_{X\times S/S}$-regular holonomic (Theorem 4.15(iii)).• For any coherent
 $\mathcal {D}_{X\times S/S}(*D)$-module of D-type, the morphism
$\mathcal {D}_{X\times S/S}(*D)$-module of D-type, the morphism  $\psi$ is injective. Indeed, according to the first point of Definition 4.23, the restriction of
$\psi$ is injective. Indeed, according to the first point of Definition 4.23, the restriction of  $\psi$ to
$\psi$ to  $X^*\times S$ is an isomorphism. The assertion follows from the
$X^*\times S$ is an isomorphism. The assertion follows from the  $\mathcal {O}$-quasi-coherence of
$\mathcal {O}$-quasi-coherence of  $\mathcal {L}$ (cf. Remark 2.5(ii)). We thus identify
$\mathcal {L}$ (cf. Remark 2.5(ii)). We thus identify  $\mathcal {L}$ with a
$\mathcal {L}$ with a  $\mathcal {D}_{X\times S/S}(*D)$-submodule of
$\mathcal {D}_{X\times S/S}(*D)$-submodule of  $j_*E_L$.
$j_*E_L$.• Due to Definition 4.23(b), Proposition 4.25(ii) amounts to holonomicity of
 $\mathcal {L}$ (in particular,
$\mathcal {L}$ (in particular,  $\mathcal {D}_{X\times S/S}$-coherence).
$\mathcal {D}_{X\times S/S}$-coherence).
Proof of Proposition 4.25(i). We assume that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free of finite rank. We can mimic the end of the proof of [Reference Monteiro Fernandes and SabbahMFS19, Proposition 2.11] to directly show that
$\mathcal {O}_S$-locally free of finite rank. We can mimic the end of the proof of [Reference Monteiro Fernandes and SabbahMFS19, Proposition 2.11] to directly show that ![]() $\psi$ is an isomorphism
$\psi$ is an isomorphism ![]() $\mathcal {L}\stackrel {\sim }{\longrightarrow }\widetilde E_L$ because, although in [Reference Monteiro Fernandes and SabbahMFS19, Proposition 2.11] we assumed the
$\mathcal {L}\stackrel {\sim }{\longrightarrow }\widetilde E_L$ because, although in [Reference Monteiro Fernandes and SabbahMFS19, Proposition 2.11] we assumed the ![]() $\mathcal {D}_{X\times S/S}$-coherence of
$\mathcal {D}_{X\times S/S}$-coherence of ![]() $\mathcal {L}$, that proof works under the weaker assumption of its
$\mathcal {L}$, that proof works under the weaker assumption of its ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherence. This shows Proposition 4.25(i). In particular, this implies the
$\mathcal {D}_{X\times S/S}(*Y)$-coherence. This shows Proposition 4.25(i). In particular, this implies the ![]() $\mathcal {D}_{X\times S/S}$-regular holonomicity of
$\mathcal {D}_{X\times S/S}$-regular holonomicity of ![]() $\mathcal {L}$.
$\mathcal {L}$.
Proof of Proposition 4.25(ii). We now prove the holonomicity of ![]() $\mathcal {L}$ by assuming only that
$\mathcal {L}$ by assuming only that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-coherent. As in the proof of Theorem 4.15(iii), we argue by induction on the dimension of
$\mathcal {O}_S$-coherent. As in the proof of Theorem 4.15(iii), we argue by induction on the dimension of ![]() $S$. The case where
$S$. The case where ![]() $S$ is a point is well-known [Reference Kashiwara and KawaiKK81, Theorem 2.3.2]. We assume that the result holds if
$S$ is a point is well-known [Reference Kashiwara and KawaiKK81, Theorem 2.3.2]. We assume that the result holds if ![]() $\dim S\leqslant d-1$ (
$\dim S\leqslant d-1$ (![]() $d\geqslant 1$) and that
$d\geqslant 1$) and that ![]() $\dim S=d$.
$\dim S=d$.
Step 1: the case where ![]() $G$ is a torsion
$G$ is a torsion ![]() $\mathcal {O}_S$-module. As we work locally, we can assume that the support of
$\mathcal {O}_S$-module. As we work locally, we can assume that the support of ![]() $G$ is contained in a hypersurface
$G$ is contained in a hypersurface ![]() $T$ of
$T$ of ![]() $S$, having equation
$S$, having equation ![]() $h=0$, endowed with a finite morphism
$h=0$, endowed with a finite morphism ![]() $q$ to
$q$ to ![]() $S'$ of dimension
$S'$ of dimension ![]() $d-1$, and that
$d-1$, and that ![]() $h^kG=0$ for some
$h^kG=0$ for some ![]() $k\geqslant 1$. We claim that any local section
$k\geqslant 1$. We claim that any local section ![]() $m$ of
$m$ of ![]() $\mathcal {L}$ is annihilated by
$\mathcal {L}$ is annihilated by ![]() $h^k$. Indeed, for any such
$h^k$. Indeed, for any such ![]() $m$,
$m$, ![]() $h^km$ is zero on
$h^km$ is zero on ![]() $X^*\times S$ and we can apply the result of Remark 2.5(ii).
$X^*\times S$ and we can apply the result of Remark 2.5(ii).
Therefore, ![]() $\operatorname {Supp}_S\mathcal {L}$ is contained in
$\operatorname {Supp}_S\mathcal {L}$ is contained in ![]() $T$. By the induction hypothesis and the equivalence recalled in Setting 3.12, we deduce that
$T$. By the induction hypothesis and the equivalence recalled in Setting 3.12, we deduce that ![]() $\mathcal {L}$ is
$\mathcal {L}$ is ![]() $q^{-1}\mathcal {D}_{X\times S'/S'}$-holonomic, hence, arguing as in Remark 3.13, we conclude that
$q^{-1}\mathcal {D}_{X\times S'/S'}$-holonomic, hence, arguing as in Remark 3.13, we conclude that ![]() $\mathcal {L}$ is
$\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S/S}$-holonomic, as desired.
$\mathcal {D}_{X\times S/S}$-holonomic, as desired.
Step 2: the case where ![]() $G_\mathrm {tf}$ is
$G_\mathrm {tf}$ is ![]() $\mathcal {O}_S$-locally free. We consider the exact sequence (4.1) and we assume that
$\mathcal {O}_S$-locally free. We consider the exact sequence (4.1) and we assume that ![]() $G_\mathrm {tf}$ is
$G_\mathrm {tf}$ is ![]() $\mathcal {O}_S$-locally free. We also consider the similar exact sequence
$\mathcal {O}_S$-locally free. We also consider the similar exact sequence ![]() $0\rightarrow \mathcal {L}_\mathrm {t}\rightarrow \mathcal {L}\rightarrow \mathcal {L}_\mathrm {tf}\to 0$. Let us prove that
$0\rightarrow \mathcal {L}_\mathrm {t}\rightarrow \mathcal {L}\rightarrow \mathcal {L}_\mathrm {tf}\to 0$. Let us prove that ![]() $\mathcal {L}_\mathrm {tf}$ is of D-type. First,
$\mathcal {L}_\mathrm {tf}$ is of D-type. First, ![]() $\mathcal {L}_\mathrm {t}$ is easily seen to be
$\mathcal {L}_\mathrm {t}$ is easily seen to be ![]() $\mathcal {D}_{X\times S/S}(*D)$-coherent, hence so is
$\mathcal {D}_{X\times S/S}(*D)$-coherent, hence so is ![]() $\mathcal {L}_\mathrm {tf}$. Next,
$\mathcal {L}_\mathrm {tf}$. Next, ![]() $\mathcal {L}_\mathrm {tf}$ satisfies the first point of Definition 4.23, with local system
$\mathcal {L}_\mathrm {tf}$ satisfies the first point of Definition 4.23, with local system ![]() $p^{-1}G_\mathrm {tf}$.
$p^{-1}G_\mathrm {tf}$.
For the second point, we note that the image of ![]() $i^*_s\mathcal {L}_\mathrm {t}\rightarrow i^*_s\mathcal {L}$ is
$i^*_s\mathcal {L}_\mathrm {t}\rightarrow i^*_s\mathcal {L}$ is ![]() $\mathcal {D}_{X}$-coherent because
$\mathcal {D}_{X}$-coherent because ![]() $i^*_s\mathcal {L}$ is so and
$i^*_s\mathcal {L}$ is so and ![]() $i^*_s\mathcal {L}_\mathrm {t}$ is
$i^*_s\mathcal {L}_\mathrm {t}$ is ![]() $\mathcal {O}$-quasi-coherent. As a consequence, it is
$\mathcal {O}$-quasi-coherent. As a consequence, it is ![]() $\mathcal {D}_{X}$-regular holonomic because
$\mathcal {D}_{X}$-regular holonomic because ![]() $i^*_s\mathcal {L}$ is so, and thus
$i^*_s\mathcal {L}$ is so, and thus ![]() $i^*_s\mathcal {L}_\mathrm {tf}$ is regular holonomic. On the other hand, for
$i^*_s\mathcal {L}_\mathrm {tf}$ is regular holonomic. On the other hand, for ![]() $j<0$,
$j<0$, ![]() $L^ji^*_s\mathcal {L}_\mathrm {tf}$ is
$L^ji^*_s\mathcal {L}_\mathrm {tf}$ is ![]() $\mathcal {O}$-quasi-coherent and supported on
$\mathcal {O}$-quasi-coherent and supported on ![]() $D$ by our assumption on
$D$ by our assumption on ![]() $G_\mathrm {tf}$, so
$G_\mathrm {tf}$, so ![]() $L^ji^*_s\mathcal {L}_\mathrm {tf}=0$ by Lemma 2.3(ii).
$L^ji^*_s\mathcal {L}_\mathrm {tf}=0$ by Lemma 2.3(ii).
In conclusion, ![]() $\mathcal {L}_\mathrm {tf}$ is of D-type, and we also deduce that
$\mathcal {L}_\mathrm {tf}$ is of D-type, and we also deduce that ![]() $\mathcal {L}_\mathrm {t}$ is of D-type. By step 1 and Proposition 4.25(i),
$\mathcal {L}_\mathrm {t}$ is of D-type. By step 1 and Proposition 4.25(i), ![]() $\mathcal {L}$ is holonomic if
$\mathcal {L}$ is holonomic if ![]() $G_\mathrm {tf}$ is
$G_\mathrm {tf}$ is ![]() $\mathcal {O}_S$-locally free.
$\mathcal {O}_S$-locally free.
Step 3: the general case. Let ![]() $\pi :S'\rightarrow S$ be a projective modification as in Proposition 4.16 such that the
$\pi :S'\rightarrow S$ be a projective modification as in Proposition 4.16 such that the ![]() $S'$-torsion-free quotient of
$S'$-torsion-free quotient of ![]() $\pi ^*G_\mathrm {tf}$ is
$\pi ^*G_\mathrm {tf}$ is ![]() $\mathcal {O}_{S'}$-locally free. The
$\mathcal {O}_{S'}$-locally free. The ![]() $S'$-torsion-free quotient of
$S'$-torsion-free quotient of ![]() $\pi ^*G$, being equal to it, is then
$\pi ^*G$, being equal to it, is then ![]() $\mathcal {O}_{S'}$-locally free.
$\mathcal {O}_{S'}$-locally free.
By Lemma 4.24, ![]() $L\pi ^*\mathcal {L}$ has cohomology in
$L\pi ^*\mathcal {L}$ has cohomology in ![]() $\mathrm {Mod}_D(\mathcal {D}_{X\times S'/S'}(*D))$. We can therefore apply steps 1 and 2 to deduce that
$\mathrm {Mod}_D(\mathcal {D}_{X\times S'/S'}(*D))$. We can therefore apply steps 1 and 2 to deduce that ![]() $\pi ^*\mathcal {L}$ is
$\pi ^*\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S'/S'}$-holonomic, and it is regular by Definition 4.23(b). It is moreover
$\mathcal {D}_{X\times S'/S'}$-holonomic, and it is regular by Definition 4.23(b). It is moreover ![]() $\pi$-good (cf. Lemma 2.13). Hence,
$\pi$-good (cf. Lemma 2.13). Hence, ![]() $\pi _*\pi ^*\mathcal {L}$ is
$\pi _*\pi ^*\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S/S}$-regular holonomic (Theorem 3.15).
$\mathcal {D}_{X\times S/S}$-regular holonomic (Theorem 3.15).
As ![]() $\mathcal {L}$ is
$\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S/S}(*D)$-coherent, the image
$\mathcal {D}_{X\times S/S}(*D)$-coherent, the image ![]() $\mathcal {L}'$ of the adjunction morphism
$\mathcal {L}'$ of the adjunction morphism ![]() $\mathcal {L}\rightarrow \pi _*\pi ^*\mathcal {L}$ is
$\mathcal {L}\rightarrow \pi _*\pi ^*\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S/S}$-coherent, hence regular holonomic (Proposition 3.2(iii)) and its kernel is
$\mathcal {D}_{X\times S/S}$-coherent, hence regular holonomic (Proposition 3.2(iii)) and its kernel is ![]() $\mathcal {D}_{X\times S/S}(*D)$-coherent. It follows that the latter, which clearly satisfies the first point of Definition 4.23, also satisfies the second point because
$\mathcal {D}_{X\times S/S}(*D)$-coherent. It follows that the latter, which clearly satisfies the first point of Definition 4.23, also satisfies the second point because ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $\mathcal {L}'$ do so (cf. Proposition 3.2). As
$\mathcal {L}'$ do so (cf. Proposition 3.2). As ![]() $\pi$ is biholomorphic above
$\pi$ is biholomorphic above ![]() $S\smallsetminus T$ for some closed analytic subset
$S\smallsetminus T$ for some closed analytic subset ![]() $T$ of codimension
$T$ of codimension ![]() $\geqslant 2$, this kernel satisfies the assumption of step 1. It is thus
$\geqslant 2$, this kernel satisfies the assumption of step 1. It is thus ![]() $\mathcal {D}_{X\times S/S}$-holonomic, hence
$\mathcal {D}_{X\times S/S}$-holonomic, hence ![]() $\mathcal {L}$ is
$\mathcal {L}$ is ![]() $\mathcal {D}_{X\times S/S}$-holonomic, as desired.
$\mathcal {D}_{X\times S/S}$-holonomic, as desired.
Note that the assignment ![]() $\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ is a functor which takes values in the category of coherent
$\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ is a functor which takes values in the category of coherent ![]() $S$-locally constant sheaves, because the characteristic variety of
$S$-locally constant sheaves, because the characteristic variety of ![]() $\mathcal {L}_{|X^*\times S}$ is contained in the zero section.
$\mathcal {L}_{|X^*\times S}$ is contained in the zero section.
Proposition 4.26 The category of strict regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules of D-type with singularities along
$\mathcal {D}_{X\times S/S}$-modules of D-type with singularities along ![]() $D$ is equivalent to the category of
$D$ is equivalent to the category of ![]() $S$-locally constant sheaves on
$S$-locally constant sheaves on ![]() $X^*\times S$ which are
$X^*\times S$ which are ![]() $p^{-1}\mathcal {O}_S$-locally free of finite rank, under the correspondences
$p^{-1}\mathcal {O}_S$-locally free of finite rank, under the correspondences ![]() $\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ and
$\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ and ![]() $L\mapsto \mathcal {L}=\widetilde E_L$.
$L\mapsto \mathcal {L}=\widetilde E_L$.
Proof. Owing to the Riemann–Hilbert correspondence on ![]() $X^*\times S$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Remark A.10]), we have
$X^*\times S$ (cf. [Reference Monteiro Fernandes and SabbahMFS19, Remark A.10]), we have ![]() $\mathcal {L}_{|X^*\times S}\simeq (\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X\times S/S}\otimes \operatorname {Id})=E_L$. As the natural morphism
$\mathcal {L}_{|X^*\times S}\simeq (\mathcal {O}_{X^*\times S}\otimes _{p^{-1}\mathcal {O}_S}L,\mathrm {d}_{X\times S/S}\otimes \operatorname {Id})=E_L$. As the natural morphism ![]() $\mathcal {L}\rightarrow j_*E_L$ sends isomorphically
$\mathcal {L}\rightarrow j_*E_L$ sends isomorphically ![]() $\mathcal {L}$ to
$\mathcal {L}$ to ![]() $\widetilde E_L$ (Proposition 4.25(i)), the functor
$\widetilde E_L$ (Proposition 4.25(i)), the functor ![]() $L\mapsto \widetilde E_L$ from the category of
$L\mapsto \widetilde E_L$ from the category of ![]() $S$-locally constant sheaves on
$S$-locally constant sheaves on ![]() $X^*\times S$ which are
$X^*\times S$ which are ![]() $p^{-1}\mathcal {O}_S$-locally free of finite rank to that of regular holonomic
$p^{-1}\mathcal {O}_S$-locally free of finite rank to that of regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules of D-type is essentially surjective. That it is fully faithful has been proved in Theorem 4.15(ii).
$\mathcal {D}_{X\times S/S}$-modules of D-type is essentially surjective. That it is fully faithful has been proved in Theorem 4.15(ii).
4.e Proof of Theorem 1
Although the next proposition is not general enough to prove Theorem 1, it will be one of the main tools for its proof.
Let ![]() $f:X\rightarrow Y$ be a morphism of real or complex analytic manifolds, we denote by
$f:X\rightarrow Y$ be a morphism of real or complex analytic manifolds, we denote by ![]() $\mathcal {D}_{{Y\leftarrow X}/S}$ and by
$\mathcal {D}_{{Y\leftarrow X}/S}$ and by ![]() $\mathcal {D}_{{X\rightarrow Y}/S}$ the relative transfer bi-modules.
$\mathcal {D}_{{X\rightarrow Y}/S}$ the relative transfer bi-modules.
Proposition 4.27 Let ![]() $\mathcal {M}$ be a regular holonomic
$\mathcal {M}$ be a regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-module with
$\mathcal {D}_{X\times S/S}$-module with ![]() $X$-support
$X$-support ![]() $Z=\mathop {\textstyle \bigcup } _iZ_i$ (see (2.7)). Let
$Z=\mathop {\textstyle \bigcup } _iZ_i$ (see (2.7)). Let ![]() $Y\subset X$ be a hypersurface such that
$Y\subset X$ be a hypersurface such that ![]() $Y\supset Z_i$ if
$Y\supset Z_i$ if ![]() $\dim Z_i<\dim Z$, and
$\dim Z_i<\dim Z$, and ![]() $Z_o:= Z\smallsetminus (Y\cap Z)$ is smooth of pure dimension
$Z_o:= Z\smallsetminus (Y\cap Z)$ is smooth of pure dimension ![]() $\dim Z$. Then the localized
$\dim Z$. Then the localized ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}(*Y)$ is regular holonomic and locally isomorphic to the projective pushforward of a relative
$\mathcal {M}(*Y)$ is regular holonomic and locally isomorphic to the projective pushforward of a relative ![]() $\mathcal {D}$-module of D-type.
$\mathcal {D}$-module of D-type.
Proof. The question is local. The assumption on ![]() $Y$ implies that the characteristic variety of
$Y$ implies that the characteristic variety of ![]() $\mathcal {M}_{|(X\smallsetminus Y)\times S}$ is contained in
$\mathcal {M}_{|(X\smallsetminus Y)\times S}$ is contained in ![]() $(T^*_{Z_o}X)\times S$. By Kashiwara's equivalence,
$(T^*_{Z_o}X)\times S$. By Kashiwara's equivalence, ![]() $\mathcal {M}_{|(X\smallsetminus Y)\times S}$ is the pushforward by the inclusion map of a coherent
$\mathcal {M}_{|(X\smallsetminus Y)\times S}$ is the pushforward by the inclusion map of a coherent ![]() $\mathcal {O}_{Z_o\times S}$-module with flat relative connection, which is thus of the form
$\mathcal {O}_{Z_o\times S}$-module with flat relative connection, which is thus of the form ![]() $(\mathcal {O}_{Z_o\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{Z_o\times S/S})$ for some coherent locally constant
$(\mathcal {O}_{Z_o\times S}\otimes _{p^{-1}\mathcal {O}_S} L,\mathrm {d}_{Z_o\times S/S})$ for some coherent locally constant ![]() $p^{-1}_{Z_o}\mathcal {O}_S$-module
$p^{-1}_{Z_o}\mathcal {O}_S$-module ![]() $L$.
$L$.
One can find a complex manifold ![]() $X'$ together with a divisor with normal crossings
$X'$ together with a divisor with normal crossings ![]() $Y'\subset X'$ and a projective morphism
$Y'\subset X'$ and a projective morphism ![]() $f:X'\rightarrow X$ which induces a biholomorphism
$f:X'\rightarrow X$ which induces a biholomorphism ![]() $X'\smallsetminus Y'\stackrel {\sim }{\longrightarrow } Z_o$ (cf., e.g., [Reference Aroca, Hironaka and VicenteAHV18, Prologue, Theorem 4]). We set
$X'\smallsetminus Y'\stackrel {\sim }{\longrightarrow } Z_o$ (cf., e.g., [Reference Aroca, Hironaka and VicenteAHV18, Prologue, Theorem 4]). We set ![]() $\delta =\dim Z-\dim X=\dim X'-\dim X\leqslant 0$. For each
$\delta =\dim Z-\dim X=\dim X'-\dim X\leqslant 0$. For each ![]() $\ell$, we consider the
$\ell$, we consider the ![]() $\mathcal {D}_{X'\times S/S}$-module
$\mathcal {D}_{X'\times S/S}$-module ![]() $\mathcal {M}^{\prime \ell }:=\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$. Although it is not yet known to be coherent, it is
$\mathcal {M}^{\prime \ell }:=\mathcal {H}^\ell {}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$. Although it is not yet known to be coherent, it is ![]() $f$-
$f$-![]() $\mathcal {O}$-good in the sense of Definition 2.2 (Proposition 2.11(i)). By considering the filtration by the order of the pole along
$\mathcal {O}$-good in the sense of Definition 2.2 (Proposition 2.11(i)). By considering the filtration by the order of the pole along ![]() $Y'$, one checks that
$Y'$, one checks that ![]() $\mathcal {M}^{\prime \ell }(*Y')$ is also
$\mathcal {M}^{\prime \ell }(*Y')$ is also ![]() $f$-
$f$-![]() $\mathcal {O}$-good (cf. Remark 2.5(i)).
$\mathcal {O}$-good (cf. Remark 2.5(i)).
If ![]() $\ell \neq \delta$, the sheaf-theoretic restriction of
$\ell \neq \delta$, the sheaf-theoretic restriction of ![]() $\mathcal {M}^{\prime \ell }$ to
$\mathcal {M}^{\prime \ell }$ to ![]() $(X'\smallsetminus Y')\times S$ is zero, therefore
$(X'\smallsetminus Y')\times S$ is zero, therefore ![]() $\mathcal {M}^{\prime \ell }(*Y')=0$ owing to
$\mathcal {M}^{\prime \ell }(*Y')=0$ owing to ![]() $\mathcal {O}$-quasi-coherence (cf. Lemma 2.3(ii)). As
$\mathcal {O}$-quasi-coherence (cf. Lemma 2.3(ii)). As ![]() $\mathcal {O}_{X'\times S}(*Y')$ is flat over
$\mathcal {O}_{X'\times S}(*Y')$ is flat over ![]() $\mathcal {O}_{X'\times S}$, we conclude that
$\mathcal {O}_{X'\times S}$, we conclude that
We can interpret ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*(\mathcal {M}(*Y))$ as the pullback of
${}_{\scriptscriptstyle \mathrm {D}}f^*(\mathcal {M}(*Y))$ as the pullback of ![]() $\mathcal {M}(*Y)$ as a
$\mathcal {M}(*Y)$ as a ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module. As
$\mathcal {D}_{X\times S/S}(*Y)$-module. As ![]() $f$ is a modification and
$f$ is a modification and ![]() $Y'=f^{-1}(Y)$, we have
$Y'=f^{-1}(Y)$, we have
 \begin{align} \mathcal{D}_{X'\times S/S}(*Y')&\simeq\mathcal{O}_{X'\times S}(*Y')\otimes_{f^{-1}(\mathcal{O}_{X\times S}(*Y))} f^{-1}\mathcal{D}_{X\times S/S}(*Y)\nonumber\\ &=\mathcal{D}_{X'\rightarrow X/S}(*Y') \end{align}
\begin{align} \mathcal{D}_{X'\times S/S}(*Y')&\simeq\mathcal{O}_{X'\times S}(*Y')\otimes_{f^{-1}(\mathcal{O}_{X\times S}(*Y))} f^{-1}\mathcal{D}_{X\times S/S}(*Y)\nonumber\\ &=\mathcal{D}_{X'\rightarrow X/S}(*Y') \end{align}
(in local coordinates ![]() $x'$ in
$x'$ in ![]() $X'$ and
$X'$ and ![]() $x$ in
$x$ in ![]() $X$, the determinant of the matrix expressing
$X$, the determinant of the matrix expressing ![]() $\partial _{x'_i}$ in terms of
$\partial _{x'_i}$ in terms of ![]() $\partial _{x_j}$ is invertible in
$\partial _{x_j}$ is invertible in ![]() $\mathcal {O}_{X'\times S}(*Y')$). It follows that
$\mathcal {O}_{X'\times S}(*Y')$). It follows that ![]() $\mathcal {M}^{\prime \delta }(*Y')=\mathcal {D}_{X'\times S/S}(*Y')\otimes _{f^{-1}\mathcal {D}_{X\times S/S}(*Y)}f^{-1}\mathcal {M}(*Y)$ is
$\mathcal {M}^{\prime \delta }(*Y')=\mathcal {D}_{X'\times S/S}(*Y')\otimes _{f^{-1}\mathcal {D}_{X\times S/S}(*Y)}f^{-1}\mathcal {M}(*Y)$ is ![]() $\mathcal {D}_{X'\times S/S}(*Y')$-coherent.
$\mathcal {D}_{X'\times S/S}(*Y')$-coherent.
As ![]() $Li_s^*$ commutes with
$Li_s^*$ commutes with ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*$,
${}_{\scriptscriptstyle \mathrm {D}}f^*$, ![]() $\mathcal {M}^{\prime \delta }(*Y')$ is
$\mathcal {M}^{\prime \delta }(*Y')$ is ![]() $\mathcal {D}_{X'\times S/S}(*Y')$-coherent of D-type (Definition 4.23) so, by Proposition 4.25(ii), it is
$\mathcal {D}_{X'\times S/S}(*Y')$-coherent of D-type (Definition 4.23) so, by Proposition 4.25(ii), it is ![]() $\mathcal {D}_{X'\times S/S}$-regular holonomic. As
$\mathcal {D}_{X'\times S/S}$-regular holonomic. As ![]() $\mathcal {M}^{\prime \delta }(*Y')$ is
$\mathcal {M}^{\prime \delta }(*Y')$ is ![]() $f$-
$f$-![]() $\mathcal {O}$-good and
$\mathcal {O}$-good and ![]() $\mathcal {D}_{X'\times S/S}$-coherent, it is
$\mathcal {D}_{X'\times S/S}$-coherent, it is ![]() $f$-good.
$f$-good.
According to [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.4], ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_*(\mathcal {M}^{\prime \delta }(*Y'))$ has regular holonomic cohomology. Furthermore, because
${}_{\scriptscriptstyle \mathrm {D}}f_*(\mathcal {M}^{\prime \delta }(*Y'))$ has regular holonomic cohomology. Furthermore, because ![]() $\mathcal {H}^j({}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}^{\prime \delta }(*Y'))$ is supported on
$\mathcal {H}^j({}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}^{\prime \delta }(*Y'))$ is supported on ![]() $Y\times S$ for
$Y\times S$ for ![]() $j\neq 0$, and since
$j\neq 0$, and since ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_*(\mathcal {M}^{\prime \delta }(*Y'))\simeq ({}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}^{\prime \delta })(*Y)$, we have
${}_{\scriptscriptstyle \mathrm {D}}f_*(\mathcal {M}^{\prime \delta }(*Y'))\simeq ({}_{\scriptscriptstyle \mathrm {D}}f_*\mathcal {M}^{\prime \delta })(*Y)$, we have
On the other hand, there is a natural adjunction morphism (cf. [Reference KashiwaraKas03, Lemma 4.28 and Proposition 4.34])
which induces a morphism of coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-modules
$\mathcal {D}_{X\times S/S}(*Y)$-modules
where the left-hand side is ![]() $\mathcal {D}_{X\times S/S}$-coherent and regular holonomic. Its cokernel is zero on
$\mathcal {D}_{X\times S/S}$-coherent and regular holonomic. Its cokernel is zero on ![]() $(X\smallsetminus Y)\times S$ and
$(X\smallsetminus Y)\times S$ and ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent, hence it is zero according to Lemma 2.3(ii), so that this morphism is an isomorphism. In conclusion,
$\mathcal {D}_{X\times S/S}(*Y)$-coherent, hence it is zero according to Lemma 2.3(ii), so that this morphism is an isomorphism. In conclusion, ![]() $\mathcal {M}(*Y)$ is regular holonomic.
$\mathcal {M}(*Y)$ is regular holonomic.
Corollary 4.31 Let ![]() $\mathcal {M}$ be a regular holonomic
$\mathcal {M}$ be a regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-module and let
$\mathcal {D}_{X\times S/S}$-module and let ![]() $Y$ be any hypersurface in
$Y$ be any hypersurface in ![]() $X$. Then the localized
$X$. Then the localized ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $\mathcal {M}(*Y)$ is regular holonomic (hence,
$\mathcal {M}(*Y)$ is regular holonomic (hence, ![]() $\mathcal {D}_{X\times S/S}$-coherent).
$\mathcal {D}_{X\times S/S}$-coherent).
Proof. The question is local on ![]() $X\times S$. Let
$X\times S$. Let ![]() $Z$ denote the
$Z$ denote the ![]() $X$-support of
$X$-support of ![]() $\mathcal {M}$. We argue by induction on the dimension of
$\mathcal {M}$. We argue by induction on the dimension of ![]() $Z$. The case where
$Z$. The case where ![]() $\dim Z=0$ is clear because either
$\dim Z=0$ is clear because either ![]() $Z\subset Y$ and then
$Z\subset Y$ and then ![]() $\mathcal {M}(*Y)=0$, or
$\mathcal {M}(*Y)=0$, or ![]() $Z\not \subset Y$ and then
$Z\not \subset Y$ and then ![]() $\mathcal {M}(*Y)=\mathcal {M}$.
$\mathcal {M}(*Y)=\mathcal {M}$.
Let ![]() $Y'$ be a hypersurface satisfying the properties as in Proposition 4.27. Then
$Y'$ be a hypersurface satisfying the properties as in Proposition 4.27. Then ![]() $Y\cup Y'$ satisfies the same properties. We consider the following commutative diagram.
$Y\cup Y'$ satisfies the same properties. We consider the following commutative diagram.

By Proposition 4.27, the terms of the top horizontal line, together with ![]() $\mathcal {M}(*(Y'\cup Y))$, are regular holonomic. On the other hand, the support of the regular holonomic modules
$\mathcal {M}(*(Y'\cup Y))$, are regular holonomic. On the other hand, the support of the regular holonomic modules ![]() $\Gamma _{[Y']}\mathcal {M}$ and
$\Gamma _{[Y']}\mathcal {M}$ and ![]() $R^1\Gamma _{[Y']}\mathcal {M}$ is of dimension
$R^1\Gamma _{[Y']}\mathcal {M}$ is of dimension ![]() $<\dim Z$, hence the assertion holds for these modules by the induction hypothesis, and the extreme terms of the lower horizontal line are regular holonomic. It follows that the remaining term
$<\dim Z$, hence the assertion holds for these modules by the induction hypothesis, and the extreme terms of the lower horizontal line are regular holonomic. It follows that the remaining term ![]() $\mathcal {M}(*Y)$ is regular holonomic.
$\mathcal {M}(*Y)$ is regular holonomic.
Corollary 4.32 Let ![]() $\mathcal {M}$ be a regular holonomic
$\mathcal {M}$ be a regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-module and let
$\mathcal {D}_{X\times S/S}$-module and let ![]() $Y$ be any closed analytic subset in
$Y$ be any closed analytic subset in ![]() $X$. Then
$X$. Then ![]() $R\Gamma _{[Y]}\mathcal {M}$ belongs to
$R\Gamma _{[Y]}\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$.
Proof. The question is local. The case of a hypersurface follows from Corollary 4.31. The general case follows by writing locally ![]() $Y$ as the intersection of hypersurfaces.
$Y$ as the intersection of hypersurfaces.
Corollary 4.33 Let ![]() $Y$ be a closed hypersurface of
$Y$ be a closed hypersurface of ![]() $X$ and let
$X$ and let ![]() $\mathcal {M}$ be a coherent
$\mathcal {M}$ be a coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module
$\mathcal {D}_{X\times S/S}(*Y)$-module ![]() $\mathcal {L}$ of D-type. Then
$\mathcal {L}$ of D-type. Then ![]() $\mathcal {M}$ belongs to
$\mathcal {M}$ belongs to ![]() $\mathrm {Mod}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$.
$\mathrm {Mod}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$.
Proof. This is obtained by the arguments used in the proof of Proposition 4.27.
Proof of Theorem 1 We regard the morphism ![]() $f$ as the composition of a closed inclusion and a projection. The latter case is clear, so we only consider the case where
$f$ as the composition of a closed inclusion and a projection. The latter case is clear, so we only consider the case where ![]() $f:Y\mathrel {\hookrightarrow} X$ is the inclusion of a closed submanifold. Then Corollary 4.32 implies that
$f:Y\mathrel {\hookrightarrow} X$ is the inclusion of a closed submanifold. Then Corollary 4.32 implies that ![]() $R\Gamma _{[Y]}\mathcal {M}$ is regular holonomic. By Kashiwara's equivalence, we conclude that
$R\Gamma _{[Y]}\mathcal {M}$ is regular holonomic. By Kashiwara's equivalence, we conclude that ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$ belongs to
${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{Y\times S/S})$.
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{Y\times S/S})$.
Proposition 4.34 If ![]() $\mathcal {M},\mathcal {N}$ are objects of
$\mathcal {M},\mathcal {N}$ are objects of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, then so is
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, then so is ![]() $\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}^L\mathcal {N}$.
$\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}^L\mathcal {N}$.
Proof. Recall that the tensor product has been defined in Remark 2.17. According to Theorem 1 applied to the diagonal embedding ![]() $\delta$, it is enough to prove that the
$\delta$, it is enough to prove that the ![]() $S$-external tensor product
$S$-external tensor product ![]() $\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$ is an object of
$\mathcal {M}\boxtimes ^L_\mathcal {D}\mathcal {N}$ is an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{(X\times X)\times S/S})$. Holonomicity has been observed in Remark 2.17. Regularity follows from the isomorphism
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{(X\times X)\times S/S})$. Holonomicity has been observed in Remark 2.17. Regularity follows from the isomorphism ![]() $Li_s^*(\mathcal {M}\boxtimes ^L_\mathcal {D} \mathcal {N})\simeq \mathcal {D}_{X\times X}\otimes _{\mathcal {D}_{X}\boxtimes _\mathbb {C}\mathcal {D}_{X}}(Li_s^*\mathcal {M}\boxtimes _\mathbb {C} Li_s^*\mathcal {N})$ and from the regular holonomicity of the latter as a complex in
$Li_s^*(\mathcal {M}\boxtimes ^L_\mathcal {D} \mathcal {N})\simeq \mathcal {D}_{X\times X}\otimes _{\mathcal {D}_{X}\boxtimes _\mathbb {C}\mathcal {D}_{X}}(Li_s^*\mathcal {M}\boxtimes _\mathbb {C} Li_s^*\mathcal {N})$ and from the regular holonomicity of the latter as a complex in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times X})$.
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times X})$.
Let ![]() $Y_i$ (
$Y_i$ (![]() $i=1,\ldots,p$) be hypersurfaces of
$i=1,\ldots,p$) be hypersurfaces of ![]() $X$ defined as the zero set of holomorphic functions
$X$ defined as the zero set of holomorphic functions ![]() $h_i:X\rightarrow \mathbb {C}$, set
$h_i:X\rightarrow \mathbb {C}$, set ![]() $Y=\mathop {\textstyle \bigcup } _iY_i$ and let
$Y=\mathop {\textstyle \bigcup } _iY_i$ and let ![]() $\mathcal {N}$ be a
$\mathcal {N}$ be a ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module. We regard
$\mathcal {D}_{X\times S/S}(*Y)$-module. We regard ![]() $\mathcal {N}$ as an
$\mathcal {N}$ as an ![]() $\mathcal {O}_{X\times S}(*Y)$-module with flat relative connection
$\mathcal {O}_{X\times S}(*Y)$-module with flat relative connection ![]() $\nabla$, and for a tuple
$\nabla$, and for a tuple ![]() $\alpha =(\alpha _1,\ldots,\alpha _p)$ of holomorphic functions
$\alpha =(\alpha _1,\ldots,\alpha _p)$ of holomorphic functions ![]() $\alpha _i:S\rightarrow \mathbb {C}$, we denote by
$\alpha _i:S\rightarrow \mathbb {C}$, we denote by ![]() $\mathcal {N} h^\alpha$ the
$\mathcal {N} h^\alpha$ the ![]() $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module ![]() $\mathcal {N}$, endowed with the flat relative connection
$\mathcal {N}$, endowed with the flat relative connection ![]() $\nabla +\sum _i\alpha _i\operatorname {Id}\otimes \mathrm {d} h_i/h_i$. The functor
$\nabla +\sum _i\alpha _i\operatorname {Id}\otimes \mathrm {d} h_i/h_i$. The functor ![]() $\mathcal {N}\rightarrow \mathcal {N} h^\alpha$ is an auto-equivalence of the category
$\mathcal {N}\rightarrow \mathcal {N} h^\alpha$ is an auto-equivalence of the category ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$, as well as of
$\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*Y))$, as well as of ![]() $\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$. We have a functorial isomorphism
$\mathrm {Mod}_\mathrm {coh}(\mathcal {D}_{X\times S/S}(*Y))$. We have a functorial isomorphism ![]() $\mathcal {N} h^\alpha \simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}\mathcal {N}\simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}^L\mathcal {N}$.
$\mathcal {N} h^\alpha \simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}\mathcal {N}\simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}^L\mathcal {N}$.
Corollary 4.35 Assume that ![]() $\mathcal {M}$ is a regular holonomic
$\mathcal {M}$ is a regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-module. Then so is
$\mathcal {D}_{X\times S/S}$-module. Then so is ![]() $\mathcal {M}(*Y)h^\alpha$.
$\mathcal {M}(*Y)h^\alpha$.
Sketch of proof One checks that the coherent ![]() $\mathcal {D}_{X\times S/S}(*Y)$-module
$\mathcal {D}_{X\times S/S}(*Y)$-module ![]() $\mathcal {O}_{X\times S}(*Y)h^\alpha$ is of D-type along
$\mathcal {O}_{X\times S}(*Y)h^\alpha$ is of D-type along ![]() $Y$ by using that
$Y$ by using that ![]() $\mathcal {O}_X(*Y)h^{\alpha (s)}$ is regular holonomic for each
$\mathcal {O}_X(*Y)h^{\alpha (s)}$ is regular holonomic for each ![]() $s \in S$. Hence
$s \in S$. Hence ![]() $\mathcal {O}_{X\times S}(*Y)h^\alpha$ is regular holonomic by Corollary 4.33. Then, on noting that
$\mathcal {O}_{X\times S}(*Y)h^\alpha$ is regular holonomic by Corollary 4.33. Then, on noting that ![]() $\mathcal {M}(*Y)h^\alpha \simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}\mathcal {M}$, we conclude by applying Proposition 4.34.
$\mathcal {M}(*Y)h^\alpha \simeq \mathcal {O}_{X\times S}(*Y)h^\alpha \otimes _{\mathcal {O}_{X\times S}}\mathcal {M}$, we conclude by applying Proposition 4.34.
Example 4.36 (Generalized Mellin transform)
Let ![]() $f_1,\ldots,f_p$ be meromorphic functions on
$f_1,\ldots,f_p$ be meromorphic functions on ![]() $X$, i.e., locally each
$X$, i.e., locally each ![]() $f_i$ is the quotient of two holomorphic functions
$f_i$ is the quotient of two holomorphic functions ![]() $h_i,g_i$ without common factor. Let
$h_i,g_i$ without common factor. Let ![]() $Y$ be the union of the divisors of zeros and poles of the functions
$Y$ be the union of the divisors of zeros and poles of the functions ![]() $f_i$, i.e., locally the divisors of zeros of
$f_i$, i.e., locally the divisors of zeros of ![]() $h_i,g_i$. We also set
$h_i,g_i$. We also set ![]() $S=\mathbb {C}^p$ with its analytic topology. It is usual to denote by
$S=\mathbb {C}^p$ with its analytic topology. It is usual to denote by ![]() $\mathcal {O}_{X\times S}(*Y)f^s$ the
$\mathcal {O}_{X\times S}(*Y)f^s$ the ![]() $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module ![]() $\mathcal {O}_{X\times S}(*Y)$ equipped with the twisted connection
$\mathcal {O}_{X\times S}(*Y)$ equipped with the twisted connection ![]() $\mathrm {d}+\sum _is_i\mathrm {d} f_i/f_i$. The same argument as in Corollary 4.35 shows that
$\mathrm {d}+\sum _is_i\mathrm {d} f_i/f_i$. The same argument as in Corollary 4.35 shows that ![]() $\mathcal {O}_{X\times S}(*Y)f^s$ is regular holonomic and that, if
$\mathcal {O}_{X\times S}(*Y)f^s$ is regular holonomic and that, if ![]() $\mathcal {M}$ is a regular holonomic
$\mathcal {M}$ is a regular holonomic ![]() $\mathcal {D}_{X}$-module, then the
$\mathcal {D}_{X}$-module, then the ![]() $\mathcal {D}_{X\times S/S}$-module
$\mathcal {D}_{X\times S/S}$-module ![]() $q^*(\mathcal {M}(*Y))f^s:=q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}\mathcal {O}_{X\times S}(*Y)f^s$ (where
$q^*(\mathcal {M}(*Y))f^s:=q^*\mathcal {M}\otimes _{\mathcal {O}_{X\times S}}\mathcal {O}_{X\times S}(*Y)f^s$ (where ![]() $q:X\times S\rightarrow X$ denotes the projection) is also regular holonomic.
$q:X\times S\rightarrow X$ denotes the projection) is also regular holonomic.
Furthermore, the ![]() $\mathcal {D}_{X\times S/S}$-submodule of
$\mathcal {D}_{X\times S/S}$-submodule of ![]() $q^*(\mathcal {M}(*Y))f^s$ generated by the image of
$q^*(\mathcal {M}(*Y))f^s$ generated by the image of ![]() $q^*\mathcal {M}\otimes 1\cdot f^s$ is also regular holonomic, according to Proposition 3.2(iii), as it is clearly coherent (being locally of finite type in a coherent
$q^*\mathcal {M}\otimes 1\cdot f^s$ is also regular holonomic, according to Proposition 3.2(iii), as it is clearly coherent (being locally of finite type in a coherent ![]() $\mathcal {D}_{X\times S/S}$-module). This property is the
$\mathcal {D}_{X\times S/S}$-module). This property is the ![]() $S$-analytic variant of [Reference MaisonobeMai23, Proposition 13], with the regularity assumption however.
$S$-analytic variant of [Reference MaisonobeMai23, Proposition 13], with the regularity assumption however.
As ![]() $\mathcal {M}$ is regular holonomic, it is good, and so is
$\mathcal {M}$ is regular holonomic, it is good, and so is ![]() $q^*(\mathcal {M}(*Y))f^s$. Therefore, if
$q^*(\mathcal {M}(*Y))f^s$. Therefore, if ![]() $X$ is compact, the
$X$ is compact, the ![]() $\mathcal {D}$-module pushforward
$\mathcal {D}$-module pushforward ![]() ${}_{\scriptscriptstyle \mathrm {D}}p_*[q^*(\mathcal {M}(*Y))f^s]$ is an object of
${}_{\scriptscriptstyle \mathrm {D}}p_*[q^*(\mathcal {M}(*Y))f^s]$ is an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {O}_S)$. This is the generalized Mellin transform of
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}(\mathcal {O}_S)$. This is the generalized Mellin transform of ![]() $\mathcal {M}$ with respect to
$\mathcal {M}$ with respect to ![]() $(f_1,\ldots,f_p)$.
$(f_1,\ldots,f_p)$.
4.f Another characterization of regular holonomicity
For a closed analytic subset ![]() $Y$ of
$Y$ of ![]() $X$, we denote by
$X$, we denote by ![]() $\mathcal {O}_{\widehat {Y\times S}}= \varprojlim _{k\in \mathbb {Z}} \mathcal {O}_{X\times S}/\mathcal {J}^k$ the formal completion of
$\mathcal {O}_{\widehat {Y\times S}}= \varprojlim _{k\in \mathbb {Z}} \mathcal {O}_{X\times S}/\mathcal {J}^k$ the formal completion of ![]() $\mathcal {O}_{X\times S}$ along
$\mathcal {O}_{X\times S}$ along ![]() $Y\times S$, where
$Y\times S$, where ![]() $\mathcal {J}$ denotes the defining ideal of
$\mathcal {J}$ denotes the defining ideal of ![]() $Y\times S$ in
$Y\times S$ in ![]() $X\times S$. Let
$X\times S$. Let ![]() $i:Y\mathrel {\hookrightarrow} X$ denote the inclusion. We consider the exact sequence of sheaves supported on
$i:Y\mathrel {\hookrightarrow} X$ denote the inclusion. We consider the exact sequence of sheaves supported on ![]() $Y\times S$:
$Y\times S$:
Corollary 4.37 If ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, then the complexes
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, then the complexes
belong to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$.
Proof. If follows from Corollary 4.32 that we have ![]() $R\Gamma _{[Y]}\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, so that the complex
$R\Gamma _{[Y]}\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, so that the complex ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(R\Gamma _{[Y]}\mathcal {M}, \mathcal {O}_{X\times S})$ belongs to
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(R\Gamma _{[Y]}\mathcal {M}, \mathcal {O}_{X\times S})$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$, according to [Reference Monteiro Fernandes and SabbahMFS13, Theorem 3.7]. On the one hand, by mimicking the proof when
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$, according to [Reference Monteiro Fernandes and SabbahMFS13, Theorem 3.7]. On the one hand, by mimicking the proof when ![]() $S$ is reduced to a point (cf., e.g., [Reference MebkhoutMeb04, Corollary 2.7-2]), one finds a natural isomorphism
$S$ is reduced to a point (cf., e.g., [Reference MebkhoutMeb04, Corollary 2.7-2]), one finds a natural isomorphism
hence the ![]() $S$-
$S$-![]() $\mathbb {C}$-constructibility of the latter complex. On the other hand, we have natural isomorphisms
$\mathbb {C}$-constructibility of the latter complex. On the other hand, we have natural isomorphisms
 \begin{align*} Ri_*i^{-1}R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M}, \mathcal{O}_{X\times S})&\stackrel{\sim}{\longrightarrow} Ri_*R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(i^{-1}\mathcal{M}, i^{-1}\mathcal{O}_{X\times S})\\ &\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M},Ri_*i^{-1}\mathcal{O}_{X\times S}), \end{align*}
\begin{align*} Ri_*i^{-1}R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M}, \mathcal{O}_{X\times S})&\stackrel{\sim}{\longrightarrow} Ri_*R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(i^{-1}\mathcal{M}, i^{-1}\mathcal{O}_{X\times S})\\ &\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M},Ri_*i^{-1}\mathcal{O}_{X\times S}), \end{align*}
showing ![]() $S$-
$S$-![]() $\mathbb {C}$-constructibility of the latter complex, and therefore that of
$\mathbb {C}$-constructibility of the latter complex, and therefore that of ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}} (\mathcal {M}, \mathcal {Q}_{Y\times S})$.
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}} (\mathcal {M}, \mathcal {Q}_{Y\times S})$.
Theorem 4.38 Let ![]() $\mathcal {M}$ belong to
$\mathcal {M}$ belong to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})$. Then
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {hol}(\mathcal {D}_{X\times S/S})$. Then ![]() $\mathcal {M}$ is regular holonomic if and only if for any germ of closed analytic subset
$\mathcal {M}$ is regular holonomic if and only if for any germ of closed analytic subset ![]() $Y\subset X$,
$Y\subset X$, ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})$ is isomorphic to zero.
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})$ is isomorphic to zero.
Lemma 4.39 For any closed analytic subset ![]() $Y\subset X$ we have
$Y\subset X$ we have
Proof. Thanks to the properties of ![]() $Li^*_s$ (cf. Proposition 3.1) the result follows from Mittag-Leffler's condition because the morphisms
$Li^*_s$ (cf. Proposition 3.1) the result follows from Mittag-Leffler's condition because the morphisms ![]() $\mathcal {O}_{X\times S}/\mathcal {J}^{k+1}\rightarrow \mathcal {O}_{X\times S}/\mathcal {J}^k$ are surjective.
$\mathcal {O}_{X\times S}/\mathcal {J}^{k+1}\rightarrow \mathcal {O}_{X\times S}/\mathcal {J}^k$ are surjective.
Proof of Theorem 4.38 We first remark that the theorem holds if ![]() $S$ is reduced to a point, according to [Reference Kashiwara and KawaiKK81, (6.4.6) and (6.4.7)].
$S$ is reduced to a point, according to [Reference Kashiwara and KawaiKK81, (6.4.6) and (6.4.7)].
If ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})=0$ for all germ
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})=0$ for all germ ![]() $Y\subset X$, then for any
$Y\subset X$, then for any ![]() $s\in S$
$s\in S$
 \begin{align} R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X}}(Li^*_s\mathcal{M},\mathcal{Q}_Y)&\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X}}(Li^*_s\mathcal{M}, Li^*_s\mathcal{Q}_{Y\times S})\nonumber\\ &\simeq Li_s^*R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M}, \mathcal{Q}_{Y\times S})=0. \end{align}
\begin{align} R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X}}(Li^*_s\mathcal{M},\mathcal{Q}_Y)&\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X}}(Li^*_s\mathcal{M}, Li^*_s\mathcal{Q}_{Y\times S})\nonumber\\ &\simeq Li_s^*R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M}, \mathcal{Q}_{Y\times S})=0. \end{align}
From the preliminary remark. we conclude that ![]() $Li^*_s\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$ for any
$Li^*_s\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X})$ for any ![]() $s\in S$, hence
$s\in S$, hence ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$.
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$.
Conversely, if ![]() $\mathcal {M}$ is regular holonomic, then
$\mathcal {M}$ is regular holonomic, then ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})$ is
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})$ is ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible, and by the variant of Nakayama's lemma (cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.2]), it is zero if (and only if)
$\mathbb {C}$-constructible, and by the variant of Nakayama's lemma (cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.2]), it is zero if (and only if) ![]() $Li_s^*R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})=0$ for any
$Li_s^*R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {Q}_{Y\times S})=0$ for any ![]() $s\in S$. Reading (4.40) backwards and according to the preliminary remark, we find that the latter property is satisfied, hence
$s\in S$. Reading (4.40) backwards and according to the preliminary remark, we find that the latter property is satisfied, hence
5. Construction of the relative Riemann–Hilbert functor  $\operatorname {RH}_X^S$
$\operatorname {RH}_X^S$
In this section, we extend the definition of the functor ![]() $\operatorname {RH}_X^S$ introduced in [Reference Monteiro Fernandes and SabbahMFS19] when
$\operatorname {RH}_X^S$ introduced in [Reference Monteiro Fernandes and SabbahMFS19] when ![]() $\dim S= 1$ to the case
$\dim S= 1$ to the case ![]() $\dim S\geqslant 2$. We check that it satisfies properties similar to those explained in [Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21].
$\dim S\geqslant 2$. We check that it satisfies properties similar to those explained in [Reference Monteiro Fernandes and SabbahMFS19, Reference Fiorot, Monteiro Fernandes and SabbahFMFS21].
5.a Reminder on the subanalytic site and complements
We first recall the main results in [Reference Monteiro Fernandes and PrelliMFP21]. We consider the site in the real analytic manifold ![]() $S_\mathbb {R}$ given by the usual topology, that is, where the family
$S_\mathbb {R}$ given by the usual topology, that is, where the family ![]() $\operatorname {Op}(S)$ consisting of all open sets. On the other hand, we have the subanalytic site
$\operatorname {Op}(S)$ consisting of all open sets. On the other hand, we have the subanalytic site ![]() $X_{\mathrm {sa}}$ underlying the real analytic manifold
$X_{\mathrm {sa}}$ underlying the real analytic manifold ![]() $X_{\mathbb {R}}$ for which the family of open subsets
$X_{\mathbb {R}}$ for which the family of open subsets ![]() $\operatorname {Op}(X_{\mathrm {sa}})$ consists of subanalytic open subsets in
$\operatorname {Op}(X_{\mathrm {sa}})$ consists of subanalytic open subsets in ![]() $X_{\mathbb {R}}$. Lastly, we let
$X_{\mathbb {R}}$. Lastly, we let ![]() $X_{\mathrm {sa}}\times S$ be the subanalytic site underlying the real analytic manifold
$X_{\mathrm {sa}}\times S$ be the subanalytic site underlying the real analytic manifold ![]() $X_{\mathbb {R}}\times S_{\mathbb {R}}$, for which the family of open sets
$X_{\mathbb {R}}\times S_{\mathbb {R}}$, for which the family of open sets ![]() $\operatorname {Op}(X_{\mathrm {sa}}\times S)$ consists of those which are finite unions of products
$\operatorname {Op}(X_{\mathrm {sa}}\times S)$ consists of those which are finite unions of products ![]() $U\times V$ with
$U\times V$ with ![]() $U\in \operatorname {Op}(X_{\mathrm {sa}})$ and
$U\in \operatorname {Op}(X_{\mathrm {sa}})$ and ![]() $V$ is open in
$V$ is open in ![]() $S$. A subset
$S$. A subset ![]() $T \subset \operatorname {Op}(X_{\mathrm {sa}}\times S)$ is a covering of
$T \subset \operatorname {Op}(X_{\mathrm {sa}}\times S)$ is a covering of ![]() $W=U\times V \in \operatorname {Op}(X_{\mathrm {sa}}\times S)$ if and only if it admits a refinement
$W=U\times V \in \operatorname {Op}(X_{\mathrm {sa}}\times S)$ if and only if it admits a refinement ![]() $\{U_i\times V_j\}_{i \in I, j \in J}$ such that
$\{U_i\times V_j\}_{i \in I, j \in J}$ such that ![]() $\{U_i\}_{i \in \ I}$ is a covering of
$\{U_i\}_{i \in \ I}$ is a covering of ![]() $U$ (in
$U$ (in ![]() $X_{\mathrm {sa}}$) and
$X_{\mathrm {sa}}$) and ![]() $\{V_j\}_{j \in J}$ is a covering of
$\{V_j\}_{j \in J}$ is a covering of ![]() $V$ (in
$V$ (in ![]() $S$). In particular, when
$S$). In particular, when ![]() $U$ is relatively compact
$U$ is relatively compact ![]() $I$ is finite but
$I$ is finite but ![]() $J$ needs not to be so even if
$J$ needs not to be so even if ![]() $V$ is relatively compact.
$V$ is relatively compact.
We have the following commutative diagram, where the arrows are natural morphisms of sites induced by the inclusion of families of open subsets.

We recall that
(5.2)
 $\rho _S^{-1}$ commutes with tensor products (cf. [Reference Kashiwara and SchapiraKS06, Lemma 18.3.1(ii)(c)]) and
$\rho _S^{-1}$ commutes with tensor products (cf. [Reference Kashiwara and SchapiraKS06, Lemma 18.3.1(ii)(c)]) and  $\rho _S^{-1}\rho _{S*} \simeq \operatorname {Id}$. Furthermore,
$\rho _S^{-1}\rho _{S*} \simeq \operatorname {Id}$. Furthermore,  $\rho _S^{-1}$ admits a left adjoint
$\rho _S^{-1}$ admits a left adjoint  $\rho _{S!}$ which is exact and commutes with tensor products (cf. [Reference Monteiro Fernandes and PrelliMFP21, §3]).
$\rho _{S!}$ which is exact and commutes with tensor products (cf. [Reference Monteiro Fernandes and PrelliMFP21, §3]).
The following proposition generalizes [Reference Monteiro Fernandes and SabbahMFS19, Proposition 3.3]. Its proof is completely similar.
Proposition 5.3 The category ![]() $\mathrm {Mod}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ is acyclic for
$\mathrm {Mod}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ is acyclic for ![]() $\rho _S$:
$\rho _S$:
In particular, ![]() $\rho _{S*}$ is exact on
$\rho _{S*}$ is exact on ![]() $\mathrm {Mod}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$.
$\mathrm {Mod}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$.
The next statement corrects [Reference Monteiro Fernandes and SabbahMFS19, Proposition 3.5]. Its proof is given in the appendix.
Proposition 5.4 Let ![]() $F^\bullet$ be a bounded complex of
$F^\bullet$ be a bounded complex of ![]() $p_X^{-1}\mathcal {O}_S$-modules with
$p_X^{-1}\mathcal {O}_S$-modules with ![]() $S$-
$S$-![]() $\mathbb {R}$-constructible cohomology. Then there exists an isomorphism
$\mathbb {R}$-constructible cohomology. Then there exists an isomorphism ![]() $K^\bullet\rightarrow F^\bullet$ in
$K^\bullet\rightarrow F^\bullet$ in ![]() $\operatorname {\mathsf {D}}^-(p_X^{-1}\mathcal {O}_S)$, where
$\operatorname {\mathsf {D}}^-(p_X^{-1}\mathcal {O}_S)$, where ![]() $K^\bullet$ is a complex in
$K^\bullet$ is a complex in ![]() $\operatorname {\mathsf {C}}^-(p_X^{-1}\mathcal {O}_S)$ whose terms are locally finite sums
$\operatorname {\mathsf {C}}^-(p_X^{-1}\mathcal {O}_S)$ whose terms are locally finite sums ![]() $\mathop {\textstyle \bigoplus } _{\alpha \in A} \mathbb {C}_{U_{\alpha }\times V_{\alpha }} \otimes p_X^{-1}\mathcal {O}_S$, where the
$\mathop {\textstyle \bigoplus } _{\alpha \in A} \mathbb {C}_{U_{\alpha }\times V_{\alpha }} \otimes p_X^{-1}\mathcal {O}_S$, where the ![]() $U_{\alpha }$ are open subanalytic relatively compact in
$U_{\alpha }$ are open subanalytic relatively compact in ![]() $X$ and the
$X$ and the ![]() $V_{\alpha }$ are open relatively compact in
$V_{\alpha }$ are open relatively compact in ![]() $S$.
$S$.
Remark 5.5 Recall the diagram (5.1). From the fact that ![]() $a_*$ is fully faithful and that
$a_*$ is fully faithful and that ![]() $a^{-1}a_*=\operatorname {Id}$, we have
$a^{-1}a_*=\operatorname {Id}$, we have ![]() $\rho _{S*}=a^{-1}\rho '_*$ (thus,
$\rho _{S*}=a^{-1}\rho '_*$ (thus, ![]() $R\rho _{S*}=a^{-1}R\rho '_*$) as explained in [Reference Monteiro Fernandes and PrelliMFP21] before Proposition 3.1, we deduce that, for any open subset
$R\rho _{S*}=a^{-1}R\rho '_*$) as explained in [Reference Monteiro Fernandes and PrelliMFP21] before Proposition 3.1, we deduce that, for any open subset ![]() $U\times V\in \operatorname {Op}^\mathrm {c}(X_{\mathrm {sa}}\times S)$, the constant sheaf
$U\times V\in \operatorname {Op}^\mathrm {c}(X_{\mathrm {sa}}\times S)$, the constant sheaf ![]() $\mathbb {C}_{U\times V}$ on the site
$\mathbb {C}_{U\times V}$ on the site ![]() $X_{\mathrm {sa}}\times S$ coincides with
$X_{\mathrm {sa}}\times S$ coincides with ![]() $\rho _{S*}\mathbb {C}_{U\times V}$. Similarly,
$\rho _{S*}\mathbb {C}_{U\times V}$. Similarly,
because the isomorphisms hold true with ![]() $\rho '$ instead of
$\rho '$ instead of ![]() $\rho _S$ (cf. [Reference Monteiro Fernandes and PrelliMFP14, Lemma 3.6(2)]).
$\rho _S$ (cf. [Reference Monteiro Fernandes and PrelliMFP14, Lemma 3.6(2)]).
Remark 5.6 For any ![]() $S$, the site
$S$, the site ![]() $X_{\mathrm {sa}}\times S$ is a ringed site both relatively to the sheaf
$X_{\mathrm {sa}}\times S$ is a ringed site both relatively to the sheaf ![]() $\rho _{S*}(p_X^{-1}\mathcal {O}_S)$ and to the sheaf
$\rho _{S*}(p_X^{-1}\mathcal {O}_S)$ and to the sheaf ![]() $\rho _{S!} \mathcal {O}_{X\times S}$ (cf. [Reference Kashiwara and SchapiraKS06, p. 449]), and
$\rho _{S!} \mathcal {O}_{X\times S}$ (cf. [Reference Kashiwara and SchapiraKS06, p. 449]), and ![]() $\rho _S$ is a morphism of ringed sites in both cases. Thus, according to [Reference Kashiwara and SchapiraKS06, Lemma 18.3.1, Theorem 18.6.9],
$\rho _S$ is a morphism of ringed sites in both cases. Thus, according to [Reference Kashiwara and SchapiraKS06, Lemma 18.3.1, Theorem 18.6.9], ![]() $\rho _S^{-1}$ commutes with
$\rho _S^{-1}$ commutes with ![]() $\otimes$,
$\otimes$, ![]() $\otimes _{\rho _{S*}p_X^{-1}\mathcal {O}_S}$,
$\otimes _{\rho _{S*}p_X^{-1}\mathcal {O}_S}$, ![]() $\otimes _{\rho _{S!}\mathcal {O}_{X\times S}}$,
$\otimes _{\rho _{S!}\mathcal {O}_{X\times S}}$, ![]() $\otimes ^L_{\rho _{S*}p_X^{-1}\mathcal {O}_S}$ and
$\otimes ^L_{\rho _{S*}p_X^{-1}\mathcal {O}_S}$ and ![]() $\otimes ^L_{\rho _{S!}\mathcal {O}_{X\times S}}$. We recall that
$\otimes ^L_{\rho _{S!}\mathcal {O}_{X\times S}}$. We recall that ![]() $R\rho _{S*}p_X^{-1}\mathcal {O}_S\simeq \rho _{S!}p_X^{-1}\mathcal {O}_S$ (cf. [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.16]). Let
$R\rho _{S*}p_X^{-1}\mathcal {O}_S\simeq \rho _{S!}p_X^{-1}\mathcal {O}_S$ (cf. [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.16]). Let ![]() $\pi :S'\rightarrow S$ be a morphism of complex manifolds. As
$\pi :S'\rightarrow S$ be a morphism of complex manifolds. As ![]() $\mathcal {O}_{S'}$ is a
$\mathcal {O}_{S'}$ is a ![]() $\pi ^{-1}\mathcal {O}_S$-module,
$\pi ^{-1}\mathcal {O}_S$-module, ![]() $\rho _{S'*}(p_X^{-1}\mathcal {O}_{S'})$ is a
$\rho _{S'*}(p_X^{-1}\mathcal {O}_{S'})$ is a ![]() $\rho _{S'*}(p_X^{-1}\pi ^{-1}\mathcal {O}_S)$-module, hence a
$\rho _{S'*}(p_X^{-1}\pi ^{-1}\mathcal {O}_S)$-module, hence a ![]() $\pi ^{-1}\rho _{S*}(p_X^{-1}\mathcal {O}_S)$-module. Similarly,
$\pi ^{-1}\rho _{S*}(p_X^{-1}\mathcal {O}_S)$-module. Similarly, ![]() $\rho _{S'!}\mathcal {O}_{X\times S'}$ is a
$\rho _{S'!}\mathcal {O}_{X\times S'}$ is a ![]() $\pi ^{-1}\rho _{S!}\mathcal {O}_{X\times S}$-module. In other words,
$\pi ^{-1}\rho _{S!}\mathcal {O}_{X\times S}$-module. In other words, ![]() $\pi$ induces a morphism of ringed sites with respect to both sheaves of rings. Consequently, according to [Reference Kashiwara and SchapiraKS06, Theorem 18.6.9(i)], the derived functors
$\pi$ induces a morphism of ringed sites with respect to both sheaves of rings. Consequently, according to [Reference Kashiwara and SchapiraKS06, Theorem 18.6.9(i)], the derived functors ![]() $L\pi ^*: \operatorname {\mathsf {D}}(\rho _{S*}p_X^{-1}\mathcal {O}_S)\rightarrow \operatorname {\mathsf {D}}(\rho _{S'*}p^{-1}_X\mathcal {O}_{S'})$ respectively, (keeping the same notation
$L\pi ^*: \operatorname {\mathsf {D}}(\rho _{S*}p_X^{-1}\mathcal {O}_S)\rightarrow \operatorname {\mathsf {D}}(\rho _{S'*}p^{-1}_X\mathcal {O}_{S'})$ respectively, (keeping the same notation ![]() $\pi$ for the morphism
$\pi$ for the morphism ![]() $\operatorname {Id}\times \pi$),
$\operatorname {Id}\times \pi$), ![]() $L\pi ^*: \operatorname {\mathsf {D}}(\rho _{S!}\mathcal {O}_{X\times S})\rightarrow \operatorname {\mathsf {D}}(\rho _{S'!}\mathcal {O}_{X\times S'})$ are well-defined.
$L\pi ^*: \operatorname {\mathsf {D}}(\rho _{S!}\mathcal {O}_{X\times S})\rightarrow \operatorname {\mathsf {D}}(\rho _{S'!}\mathcal {O}_{X\times S'})$ are well-defined.
We recall that ![]() $\rho _S^{-1}R\rho _{S*}\simeq \operatorname {Id}$, that
$\rho _S^{-1}R\rho _{S*}\simeq \operatorname {Id}$, that ![]() $R\rho _{S*}$ commutes with
$R\rho _{S*}$ commutes with ![]() $R\pi _*$ and
$R\pi _*$ and ![]() $\rho _S^{-1}$ commutes with
$\rho _S^{-1}$ commutes with ![]() $\pi ^{-1}$ according to [Reference Kashiwara and SchapiraKS06, Proposition 17.5.3]. Furthermore,
$\pi ^{-1}$ according to [Reference Kashiwara and SchapiraKS06, Proposition 17.5.3]. Furthermore, ![]() $(\pi ^{-1}, \pi _*)$ is a pair of adjoint functors according to [Reference Kashiwara and SchapiraKS06, Theorem 17.5.2(i)] and
$(\pi ^{-1}, \pi _*)$ is a pair of adjoint functors according to [Reference Kashiwara and SchapiraKS06, Theorem 17.5.2(i)] and ![]() $\rho _S^{-1}$ commutes with
$\rho _S^{-1}$ commutes with ![]() $R\pi _*$, which follows by copying the proof of [Reference PrelliPre08, Proposition 2.2.1(ii)] because
$R\pi _*$, which follows by copying the proof of [Reference PrelliPre08, Proposition 2.2.1(ii)] because ![]() $\rho _S^{-1}$ admits an exact left adjoint (
$\rho _S^{-1}$ admits an exact left adjoint (![]() $\rho _{S!}$), hence takes injective sheaves to injective sheaves. (Note that, in general, we do not have
$\rho _{S!}$), hence takes injective sheaves to injective sheaves. (Note that, in general, we do not have ![]() $\pi ^{-1}R\rho _{S*}=R\rho _{S'*}\pi ^{-1}$ whereas we have
$\pi ^{-1}R\rho _{S*}=R\rho _{S'*}\pi ^{-1}$ whereas we have ![]() $\pi ^{-1}\rho _{S!}=\rho _{S'!}\pi ^{-1}$.) We thus have isomorphisms of functors
$\pi ^{-1}\rho _{S!}=\rho _{S'!}\pi ^{-1}$.) We thus have isomorphisms of functors
and, composing with the natural morphism ![]() $\operatorname {Id}\rightarrow R\rho _{S'*}\rho _{S'}^{-1}$, we deduce a natural morphism
$\operatorname {Id}\rightarrow R\rho _{S'*}\rho _{S'}^{-1}$, we deduce a natural morphism
We have
Lemma 5.7 Let ![]() $\pi : S'\rightarrow S$ be a morphism. Then we have an isomorphism of functors on
$\pi : S'\rightarrow S$ be a morphism. Then we have an isomorphism of functors on ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$ with values in
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$ with values in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(\rho _{S'*}p^{\prime -1}\mathcal {O}_{S'})$:
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(\rho _{S'*}p^{\prime -1}\mathcal {O}_{S'})$:
Proof. Let ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$. By (5.6 *) we have a morphism (recalling that
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$. By (5.6 *) we have a morphism (recalling that ![]() $R\rho _{S*}p^{-1}\mathcal {O}_S\simeq \rho _{S*}p^{-1}\mathcal {O}_S$)
$R\rho _{S*}p^{-1}\mathcal {O}_S\simeq \rho _{S*}p^{-1}\mathcal {O}_S$)
 \begin{align*} \rho_{S'*}p^{-1}\mathcal{O}_{S'}\otimes^L_{\pi^{-1} \rho_{S*}p^{-1}\mathcal{O}_{S}}\pi^{-1}R\rho_{S*}F &\longrightarrow \rho_{S'*}p^{-1}\mathcal{O}_{S'}\otimes^L_{\pi^{-1} \rho_{S*}p^{-1}\mathcal{O}_{S}}R\rho_{S'*}\pi^{-1}F\\ &\longrightarrow R\rho_{S'*}\Big(p^{-1}\mathcal{O}_{S'} \otimes^L_{\pi^{-1}p^{-1}\mathcal{O}_{S}}\pi^{-1}F\Big). \end{align*}
\begin{align*} \rho_{S'*}p^{-1}\mathcal{O}_{S'}\otimes^L_{\pi^{-1} \rho_{S*}p^{-1}\mathcal{O}_{S}}\pi^{-1}R\rho_{S*}F &\longrightarrow \rho_{S'*}p^{-1}\mathcal{O}_{S'}\otimes^L_{\pi^{-1} \rho_{S*}p^{-1}\mathcal{O}_{S}}R\rho_{S'*}\pi^{-1}F\\ &\longrightarrow R\rho_{S'*}\Big(p^{-1}\mathcal{O}_{S'} \otimes^L_{\pi^{-1}p^{-1}\mathcal{O}_{S}}\pi^{-1}F\Big). \end{align*}
This gives the desired morphism ![]() $\tau _F:L\pi ^*R\rho _{S*}(F)\rightarrow R\rho _{S'*}L\pi ^*(F)$. By Proposition A.6, [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Remark 1.8] and Remark A.8 we may assume that
$\tau _F:L\pi ^*R\rho _{S*}(F)\rightarrow R\rho _{S'*}L\pi ^*(F)$. By Proposition A.6, [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Remark 1.8] and Remark A.8 we may assume that ![]() $F=\mathbb {C}_{U\times V}\otimes p^{-1}\mathcal {O}_S$, for some relatively compact open subsets of
$F=\mathbb {C}_{U\times V}\otimes p^{-1}\mathcal {O}_S$, for some relatively compact open subsets of ![]() $X$ and
$X$ and ![]() $S$, respectively, with
$S$, respectively, with ![]() $U$ subanalytic. We have
$U$ subanalytic. We have
 \begin{align*} L\pi^*\rho_{S*}(F)&=\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes^L_{\pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)}\pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V}\otimes p^{-1}\mathcal{O}_S)\\ &\simeq \rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes^L_{\pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)}\pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V})\otimes \pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)\\ &\simeq \rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes \pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V}) \simeq\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes \rho_{S'*}\pi^{-1}(\mathbb{C}_{U\times V})\\ &\simeq\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'}\otimes \mathbb{C}_{U\times \pi^{-1}V}) \simeq \rho_{S'*}(L\pi^*F). \end{align*}
\begin{align*} L\pi^*\rho_{S*}(F)&=\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes^L_{\pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)}\pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V}\otimes p^{-1}\mathcal{O}_S)\\ &\simeq \rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes^L_{\pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)}\pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V})\otimes \pi^{-1}\rho_{S*}(p^{-1}\mathcal{O}_S)\\ &\simeq \rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes \pi^{-1}\rho_{S*}(\mathbb{C}_{U\times V}) \simeq\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'})\otimes \rho_{S'*}\pi^{-1}(\mathbb{C}_{U\times V})\\ &\simeq\rho_{S'*}(p^{\prime-1}\mathcal{O}_{S'}\otimes \mathbb{C}_{U\times \pi^{-1}V}) \simeq \rho_{S'*}(L\pi^*F). \end{align*}
5.b The construction of  $\operatorname {RH}_X^S$ and behavior under pushforward
$\operatorname {RH}_X^S$ and behavior under pushforward
For this section, we refer to the notation introduced in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, §2.2]. However, instead of making use of the morphism ![]() $\rho '$ of (5.1) as in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, §2.2], we replace it with
$\rho '$ of (5.1) as in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, §2.2], we replace it with ![]() $\rho _S$. Most proofs do not require any change.
$\rho _S$. Most proofs do not require any change.
We define the triangulated functor ![]() $\operatorname {TH}_X^S:\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)^{\mathrm {op}}\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$ by
$\operatorname {TH}_X^S:\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)^{\mathrm {op}}\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$ by
 \begin{align*} \operatorname{TH}_X^S(F)&:=\rho_{S}^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho_{S *}p^{-1}\mathcal{O}_S}(R\rho_{S *}F, \operatorname{\mathfrak{Db}}^{t,S}_{X\times S}),\\ \operatorname{RH}_X^S(F)&:=\rho_{S}^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho_{S *}p^{-1}\mathcal{O}_S}(R\rho_{S *}F, \mathcal{O}^{t,S}_{X\times S})[d_X]. \end{align*}
\begin{align*} \operatorname{TH}_X^S(F)&:=\rho_{S}^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho_{S *}p^{-1}\mathcal{O}_S}(R\rho_{S *}F, \operatorname{\mathfrak{Db}}^{t,S}_{X\times S}),\\ \operatorname{RH}_X^S(F)&:=\rho_{S}^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho_{S *}p^{-1}\mathcal{O}_S}(R\rho_{S *}F, \mathcal{O}^{t,S}_{X\times S})[d_X]. \end{align*}
If ![]() $\dim S=1$, we recover the definitions of [Reference Monteiro Fernandes and SabbahMFS19] (where we restricted to
$\dim S=1$, we recover the definitions of [Reference Monteiro Fernandes and SabbahMFS19] (where we restricted to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)^{\mathrm {op}}$):
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)^{\mathrm {op}}$):
 \begin{align*} \operatorname{TH}_X^S(F)&:=\rho'^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho'_*p^{-1}\mathcal{O}_S}(\rho'_*F, \operatorname{\mathfrak{Db}}^ {t,S,\sharp}_{X\times S}),\\ \operatorname{RH}_X^S(F)&:=\rho'^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho'_{*}p^{-1}\mathcal{O}_S}(\rho'_*F, \mathcal{O}^{t,S,\sharp}_{X\times S})[d_X]. \end{align*}
\begin{align*} \operatorname{TH}_X^S(F)&:=\rho'^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho'_*p^{-1}\mathcal{O}_S}(\rho'_*F, \operatorname{\mathfrak{Db}}^ {t,S,\sharp}_{X\times S}),\\ \operatorname{RH}_X^S(F)&:=\rho'^{-1}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\rho'_{*}p^{-1}\mathcal{O}_S}(\rho'_*F, \mathcal{O}^{t,S,\sharp}_{X\times S})[d_X]. \end{align*}
This can be seen as follows: noting that (cf. (5.1)) ![]() $\rho '_*=a_*\circ \rho _{S*}$,
$\rho '_*=a_*\circ \rho _{S*}$, ![]() $a^{-1}a_* = \operatorname {Id}$ and
$a^{-1}a_* = \operatorname {Id}$ and ![]() $a^{-1}\mathcal {O}^{t,S,\sharp }_{X\times S}=\mathcal {O}^{t,S}_{X\times S}$ (cf. [Reference Monteiro Fernandes and PrelliMFP21, §§ 3.1 and 3.2]), for
$a^{-1}\mathcal {O}^{t,S,\sharp }_{X\times S}=\mathcal {O}^{t,S}_{X\times S}$ (cf. [Reference Monteiro Fernandes and PrelliMFP21, §§ 3.1 and 3.2]), for ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$, one finds a natural morphism
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p^{-1}\mathcal {O}_S)$, one finds a natural morphism
Let us check that is an isomorphism. The question being local, we can reduce, according to Proposition 5.4, to proving the isomorphism for sheaves of the form ![]() $F=\mathbb {C}_{U\times V}\otimes p^{-1}\mathcal {O}_S$, for some open subanalytic relatively compact subset
$F=\mathbb {C}_{U\times V}\otimes p^{-1}\mathcal {O}_S$, for some open subanalytic relatively compact subset ![]() $U$ of
$U$ of ![]() $X$ and
$X$ and ![]() $V$ open in
$V$ open in ![]() $S$. Both objects become then isomorphic to
$S$. Both objects become then isomorphic to ![]() $R\Gamma _{X\times V} T\mathcal {H} om(\mathbb {C}_{U\times S}, \mathcal {O}_{X\times S})$, as follows from [Reference Monteiro Fernandes and PrelliMFP14, Propsositions 4.1 and 4.7] and [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.24].
$R\Gamma _{X\times V} T\mathcal {H} om(\mathbb {C}_{U\times S}, \mathcal {O}_{X\times S})$, as follows from [Reference Monteiro Fernandes and PrelliMFP14, Propsositions 4.1 and 4.7] and [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.24].
Let ![]() $U$ be a subanalytic open subset in
$U$ be a subanalytic open subset in ![]() $X$ and let us denote the inclusion by
$X$ and let us denote the inclusion by ![]() $j: U\times S\rightarrow X\times S$.
$j: U\times S\rightarrow X\times S$.
Lemma 5.8 (Extension in the case of an open subanalytic set)
Let ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}_{U}\mathcal {O}_S)$. Then there are natural isomorphisms in
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}_{U}\mathcal {O}_S)$. Then there are natural isomorphisms in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$
Proof. This lemma is a variant of [Reference Monteiro Fernandes and SabbahMFS19, Lemma 3.25] and its proof is similar.
We have the following variant of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 2.1] using [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.30].
Proposition 5.9 For each ![]() $s\in S$, we have an isomorphism of functors
$s\in S$, we have an isomorphism of functors
We have the following relative version of [Reference KashiwaraKas84, Theorem 4.1].
Theorem 5.10 Let ![]() $f:X\rightarrow Y$ be a morphism of real analytic manifolds, let
$f:X\rightarrow Y$ be a morphism of real analytic manifolds, let ![]() $F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_Y^{-1}\mathcal {O}_S)$. Then we have a canonical morphism in
$F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_Y^{-1}\mathcal {O}_S)$. Then we have a canonical morphism in ![]() $\operatorname {\mathsf {D}}(\mathcal {D}_{Y\times S/S})$, functorial with respect to
$\operatorname {\mathsf {D}}(\mathcal {D}_{Y\times S/S})$, functorial with respect to ![]() $F$ and compatible in a natural way with the composition of morphisms
$F$ and compatible in a natural way with the composition of morphisms
The proof is stepwise similar to that with ![]() $\dim S=1$ in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Lemma 2.5] using Proposition A.6. We omit it here and the detailed proof can be found in the arXiv version of this paper. Proposition 7.1 of [Reference KashiwaraKas84] (see also [Reference Kashiwara and SchapiraKS96, Theorem 5.7 (5.12)]) has a relative version already used in [Reference Monteiro Fernandes and SabbahMFS19], the proof of which is given in the following.
$\dim S=1$ in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Lemma 2.5] using Proposition A.6. We omit it here and the detailed proof can be found in the arXiv version of this paper. Proposition 7.1 of [Reference KashiwaraKas84] (see also [Reference Kashiwara and SchapiraKS96, Theorem 5.7 (5.12)]) has a relative version already used in [Reference Monteiro Fernandes and SabbahMFS19], the proof of which is given in the following.
Theorem 5.11 Let ![]() $f:X\rightarrow Y$ be a morphism of complex analytic manifolds, let
$f:X\rightarrow Y$ be a morphism of complex analytic manifolds, let ![]() $F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, and assume that
$F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, and assume that ![]() $f$ is proper on
$f$ is proper on ![]() $\operatorname {Supp} F$. Then there is a canonical isomorphism in
$\operatorname {Supp} F$. Then there is a canonical isomorphism in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$ which is compatible in a natural way with the composition of morphisms:
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{X\times S/S})$ which is compatible in a natural way with the composition of morphisms:
Proof. We recall (cf. [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, (4)]) that
In view of Theorem 5.10, where we replace ![]() $F$ by
$F$ by ![]() $Rf_*F$, and by adjunction, we derive a natural morphism
$Rf_*F$, and by adjunction, we derive a natural morphism
Lemma 5.14 The morphism ![]() $\mu _F$ is an isomorphism.
$\mu _F$ is an isomorphism.
The proof of this lemma, which is a relative version of [Reference Kashiwara and SchapiraKS96, Theorem 4.4], is given in the appendix and some more details are also given in the arXiv version of this article.
Applying ![]() $\operatorname {\mathit {R}\mathcal {H}\!\mathit {om}}_{\mathcal {D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal {O}_{\overline{Y}\times \overline{S}}, \bullet)[d_Y]$ to both terms of (5.13) the right term becomes
$\operatorname {\mathit {R}\mathcal {H}\!\mathit {om}}_{\mathcal {D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal {O}_{\overline{Y}\times \overline{S}}, \bullet)[d_Y]$ to both terms of (5.13) the right term becomes ![]() $\operatorname {RH}_Y^S(Rf_*F)$. For the left-hand side of (5.13) we obtain
$\operatorname {RH}_Y^S(Rf_*F)$. For the left-hand side of (5.13) we obtain
 \begin{align*} &\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{Y}\times \overline{S}}, {}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(F) )[d_Y]\\ &\quad \simeq \operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{Y}\times \overline{S}}, Rf_*(\mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}}\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \simeq Rf_*(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{f^{-1}\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(f^{-1}\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}}\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \underset{{(a)}}{\simeq} Rf_*(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{f^{-1}\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(f^{-1}\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}})\otimes^L_{\mathcal{D}_{Y_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F))[d_Y]\\\ &\quad \underset{{(b)}}{\simeq}Rf_*(\mathcal{D}_{Y\leftarrow X/S}\otimes^L_{\mathcal{D}_{X\times S/S}}(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \mathcal{D}_{ X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}})\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \simeq Rf_*(\mathcal{D}_{Y\leftarrow X/S}\otimes^L_{\mathcal{D}_{X\times S/S}}(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \operatorname{TH}_X^S(F)[d_X])). \end{align*}
\begin{align*} &\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{Y}\times \overline{S}}, {}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(F) )[d_Y]\\ &\quad \simeq \operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{Y}\times \overline{S}}, Rf_*(\mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}}\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \simeq Rf_*(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{f^{-1}\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(f^{-1}\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}}\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \underset{{(a)}}{\simeq} Rf_*(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{f^{-1}\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}}(f^{-1}\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}})\otimes^L_{\mathcal{D}_{Y_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F))[d_Y]\\\ &\quad \underset{{(b)}}{\simeq}Rf_*(\mathcal{D}_{Y\leftarrow X/S}\otimes^L_{\mathcal{D}_{X\times S/S}}(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \mathcal{D}_{ X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}})\otimes^L_{\mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}}}\operatorname{TH}_X^S(F)))[d_Y]\\ &\quad \simeq Rf_*(\mathcal{D}_{Y\leftarrow X/S}\otimes^L_{\mathcal{D}_{X\times S/S}}(\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \operatorname{TH}_X^S(F)[d_X])). \end{align*}
Here part (a) follows from [Reference KashiwaraKas03, (A10)] and part (b) follows from the relative version of [Reference KashiwaraKas84, Lemma 7.2] which asserts that
 \begin{align*} &\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}} (\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}})\\ &\quad \simeq \mathcal{D}_{Y\leftarrow X/S}\otimes ^L_{\mathcal{D}_{X\times S/S}}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}})[d_X-d_Y]. \end{align*}
\begin{align*} &\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{Y}\times \overline{S}/\overline{S}}} (\mathcal{O}_{\overline{Y}\times \overline{S}}, \mathcal{D}_{Y_{\mathbb{R}}\leftarrow X_{\mathbb{R}}/S_{\mathbb{R}}})\\ &\quad \simeq \mathcal{D}_{Y\leftarrow X/S}\otimes ^L_{\mathcal{D}_{X\times S/S}}\operatorname{\mathit{R}\mathcal{H}\!\mathit{om}}_{\mathcal{D}_{\overline{X}\times \overline{S}/\overline{S}}}(\mathcal{O}_{\overline{X}\times \overline{S}}, \mathcal{D}_{X_{\mathbb{R}}\times S_{\mathbb{R}}/S_{\mathbb{R}}})[d_X-d_Y]. \end{align*}
Therefore, by applying ![]() $\operatorname {\mathit {R}\mathcal {H}\!\mathit {om}}_{\mathcal {D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal {O}_{\overline{Y}\times \overline{S}}, \bullet)[d_Y]$ to the left-hand side of (5.13) we obtain an isomorphism with
$\operatorname {\mathit {R}\mathcal {H}\!\mathit {om}}_{\mathcal {D}_{\overline{Y}\times \overline{S}/\overline{S}}}(\mathcal {O}_{\overline{Y}\times \overline{S}}, \bullet)[d_Y]$ to the left-hand side of (5.13) we obtain an isomorphism with ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_!\operatorname {RH}^S_X(F)$ which concludes the construction of the morphism (5.11 *). Lemma 5.14 shows that it is an isomorphism.
${}_{\scriptscriptstyle \mathrm {D}}f_!\operatorname {RH}^S_X(F)$ which concludes the construction of the morphism (5.11 *). Lemma 5.14 shows that it is an isomorphism.
5.c Riemann–Hilbert correspondence for Deligne's extensions
We recall that, for ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$ one defines
$F\in \operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$ one defines ![]() $\boldsymbol {D}'F:=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)$ and
$\boldsymbol {D}'F:=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)$ and ![]() $\boldsymbol {D} F:=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)[2d_X]$.
$\boldsymbol {D} F:=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)[2d_X]$.
Let ![]() $L$ be a coherent
$L$ be a coherent ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$. We consider the setting of Notation 4.5 and assume that
$X^*\times S$. We consider the setting of Notation 4.5 and assume that ![]() $Y=D$ has normal crossings in
$Y=D$ has normal crossings in ![]() $X$.
$X$.
Proposition 5.15 Let ![]() $L$ be a coherent
$L$ be a coherent ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$ and let
$X^*\times S$ and let ![]() $\widetilde E_L$ be the associated Deligne extension. Then:
$\widetilde E_L$ be the associated Deligne extension. Then:
• the complex of
 $\mathcal {D}_{X\times S/S}$-modules
$\mathcal {D}_{X\times S/S}$-modules  $\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$ is isomorphic to
$\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$ is isomorphic to  $\widetilde E_L$ and thus it is regular holonomic;
$\widetilde E_L$ and thus it is regular holonomic;•
 $\operatorname {{}^\mathrm {p}Sol} \widetilde E_L\simeq j_!\boldsymbol {D}'L$.
$\operatorname {{}^\mathrm {p}Sol} \widetilde E_L\simeq j_!\boldsymbol {D}'L$.
Proof. We adapt the idea of the proof of [Reference Monteiro Fernandes and SabbahMFS19, Lemma 4.2]. Let us prove the second statement assuming the first one holds true. First, the following lemma is similar to [Reference Monteiro Fernandes and SabbahMFS19, Lemma 3.19].
Lemma 5.16 There exists an isomorphism of functors in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$:
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$:
As ![]() $\operatorname {RH}_X^S(j!\boldsymbol {D}'L)[-d_X]$ is holonomic by the first point, we have
$\operatorname {RH}_X^S(j!\boldsymbol {D}'L)[-d_X]$ is holonomic by the first point, we have
where ![]() $(*)$ follows from Lemma 5.16.
$(*)$ follows from Lemma 5.16.
Let us now prove the first statement. We set
Then, according to (5.8 **) and to [Reference Monteiro Fernandes and SabbahMFS19, Lemma 3.22], we have
 \begin{align} \widetilde E^S_L&=\rho_{S}^{-1}Rj_*R\mathcal{H}\!\mathit{om}_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S} (\rho_{S*}\boldsymbol{D}'L, j^{-1}\mathcal{O}^{t, S}_{X\times S})\nonumber\\ &\simeq \rho_S^{-1}Rj_*(\rho_{S*}L\otimes^L_{\rho_{S*}p_{X^*}^{-1} \mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S}). \end{align}
\begin{align} \widetilde E^S_L&=\rho_{S}^{-1}Rj_*R\mathcal{H}\!\mathit{om}_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S} (\rho_{S*}\boldsymbol{D}'L, j^{-1}\mathcal{O}^{t, S}_{X\times S})\nonumber\\ &\simeq \rho_S^{-1}Rj_*(\rho_{S*}L\otimes^L_{\rho_{S*}p_{X^*}^{-1} \mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S}). \end{align}We make use of the following result of [Reference Monteiro Fernandes and PrelliMFP21], the proof of which we recall with details as it is used in an essential way in the following.
Lemma 5.18 [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.32]
The complex ![]() $\widetilde E^S_L$ is concentrated in degree zero.
$\widetilde E^S_L$ is concentrated in degree zero.
Proof. Assume first that ![]() $L$ is the constant local system
$L$ is the constant local system ![]() $p_{X^*}^{-1}G$ with
$p_{X^*}^{-1}G$ with ![]() $G$ being
$G$ being ![]() $\mathcal {O}_S$-coherent. As the question is local on
$\mathcal {O}_S$-coherent. As the question is local on ![]() $X\times S$, we can assume that
$X\times S$, we can assume that ![]() $G$ admits a finite resolution
$G$ admits a finite resolution ![]() $\mathcal {O}_S^\bullet\rightarrow G$ by free
$\mathcal {O}_S^\bullet\rightarrow G$ by free ![]() $\mathcal {O}_S$-modules of finite rank. Then we have
$\mathcal {O}_S$-modules of finite rank. Then we have
 \begin{align} &\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}G\otimes_{p_{X^*}^{-1} \mathcal{O}_S}^L j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\ &\quad \stackrel{\sim}{\longleftarrow}\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S^\bullet \otimes_{p_{X^*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\ &\quad \simeq p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S} \rho_S^{-1}Rj_*j^{-1}\mathcal{O}^{t,S}_{X\times S}. \end{align}
\begin{align} &\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}G\otimes_{p_{X^*}^{-1} \mathcal{O}_S}^L j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\ &\quad \stackrel{\sim}{\longleftarrow}\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S^\bullet \otimes_{p_{X^*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\ &\quad \simeq p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S} \rho_S^{-1}Rj_*j^{-1}\mathcal{O}^{t,S}_{X\times S}. \end{align}
We recall that, according to [Reference Kashiwara and SchapiraKS01, Proposition 2.4.4 (2.4.4)], we have isomorphisms of functors on ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathbb {C}_{X_{\mathrm {sa}}\times S})$
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathbb {C}_{X_{\mathrm {sa}}\times S})$
As a consequence, we obtain an isomorphism
It follows then from [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.24(1)] applied to ![]() $\mathbb {C}_{X^*\times S}=\mathbb {C}_{X^*}\boxtimes \mathbb {C}_S$, that the latter complex is isomorphic to
$\mathbb {C}_{X^*\times S}=\mathbb {C}_{X^*}\boxtimes \mathbb {C}_S$, that the latter complex is isomorphic to ![]() $\operatorname {\mathit {T}\mathcal {H}\!\mathit {om}}(\mathbb {C}_{X^*\times S}, \mathcal {O}_{X\times S})$, so that, according to [Reference KashiwaraKas84, Lemma 7.5],
$\operatorname {\mathit {T}\mathcal {H}\!\mathit {om}}(\mathbb {C}_{X^*\times S}, \mathcal {O}_{X\times S})$, so that, according to [Reference KashiwaraKas84, Lemma 7.5],
We thus deduce from (5.19) and (5.20):
 \begin{align}
\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}G\otimes_{p_{X^*}^{-1}
\mathcal{O}_S}^L j^{-1}\mathcal{O}^{t,S}_{X\times S})&\simeq \rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}
\mathcal{O}_S^\bullet\otimes_{p_{X^*}^{-1}\mathcal{O}_S}
j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\
&\simeq
p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S}
\rho_S^{-1}Rj_*j^{-1}\mathcal{O}^{t,S}_{X\times
S}\nonumber\\ &\simeq
p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S}
\mathcal{O}_{X\times S}(*D)\nonumber\\ &
\simeq p_{X}^{-1}G\otimes_{p_{X}^{-1}\mathcal{O}_S}
\mathcal{O}_{X\times S}(*D),
\end{align}
\begin{align}
\rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}G\otimes_{p_{X^*}^{-1}
\mathcal{O}_S}^L j^{-1}\mathcal{O}^{t,S}_{X\times S})&\simeq \rho_S^{-1}Rj_*(\rho_{S*}p_{X^*}^{-1}
\mathcal{O}_S^\bullet\otimes_{p_{X^*}^{-1}\mathcal{O}_S}
j^{-1}\mathcal{O}^{t,S}_{X\times S})\nonumber\\
&\simeq
p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S}
\rho_S^{-1}Rj_*j^{-1}\mathcal{O}^{t,S}_{X\times
S}\nonumber\\ &\simeq
p_{X}^{-1}\mathcal{O}_S^\bullet\otimes_{p_{X}^{-1}\mathcal{O}_S}
\mathcal{O}_{X\times S}(*D)\nonumber\\ &
\simeq p_{X}^{-1}G\otimes_{p_{X}^{-1}\mathcal{O}_S}
\mathcal{O}_{X\times S}(*D),
\end{align}
where the latter isomorphism follows from the ![]() $p_{X}^{-1}\mathcal {O}_S$-flatness of
$p_{X}^{-1}\mathcal {O}_S$-flatness of ![]() $\mathcal {O}_{X\times S}(*D)$. We conclude that
$\mathcal {O}_{X\times S}(*D)$. We conclude that ![]() $\widetilde E^S_{p_{X^*}^{-1}G}$ is concentrated in degree zero.
$\widetilde E^S_{p_{X^*}^{-1}G}$ is concentrated in degree zero.
Let us now consider the case of a possibly non-constant ![]() $S$-local system
$S$-local system ![]() $L$ locally isomorphic to
$L$ locally isomorphic to ![]() $p^{-1}G$, with
$p^{-1}G$, with ![]() $G$ being
$G$ being ![]() $\mathcal {O}_S$-coherent. According to Remark 4.18, locally on
$\mathcal {O}_S$-coherent. According to Remark 4.18, locally on ![]() $X\times S$ we have an isomorphism of
$X\times S$ we have an isomorphism of ![]() $\mathcal {O}_{X^*\times S}$-modules
$\mathcal {O}_{X^*\times S}$-modules
and by the flatness of ![]() $\mathcal {O}_{X^*\times S}$ over
$\mathcal {O}_{X^*\times S}$ over ![]() $p_{X^*}^{-1}\mathcal {O}_S$, the same equality holds with the derived tensor product
$p_{X^*}^{-1}\mathcal {O}_S$, the same equality holds with the derived tensor product ![]() $\otimes ^L$. According to Proposition 5.3, the natural morphism
$\otimes ^L$. According to Proposition 5.3, the natural morphism ![]() $\rho _{S*}L\rightarrow R\rho _{S*}L$ is an isomorphism and [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.16] implies that
$\rho _{S*}L\rightarrow R\rho _{S*}L$ is an isomorphism and [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.16] implies that ![]() $\rho _{S!}L\simeq R\rho _{S*}L$. Recall also that, by [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.13], the functor
$\rho _{S!}L\simeq R\rho _{S*}L$. Recall also that, by [Reference Monteiro Fernandes and PrelliMFP21, Proposition 3.13], the functor ![]() $\rho _{S!}$ is exact and commutes with
$\rho _{S!}$ is exact and commutes with ![]() $\otimes$. From (5.22) we then derive
$\otimes$. From (5.22) we then derive ![]() $\mathcal {O}_{X^*\times S}$-linear isomorphisms (they are a priori not
$\mathcal {O}_{X^*\times S}$-linear isomorphisms (they are a priori not ![]() $\mathcal {D}_{X^*\times S/S}$-linear because we use a tensor product over
$\mathcal {D}_{X^*\times S/S}$-linear because we use a tensor product over ![]() $\mathcal {O}_{X^*\times S}$):
$\mathcal {O}_{X^*\times S}$):
 \begin{align*} \rho_{S*}L\otimes^L_{\rho_{S*}p_{X*}^{-1}\mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S} &\simeq(\rho_{S!}L\otimes^L_{\rho_{S!}p_{X^*}^{-1}\mathcal{O}_S}\rho_{S!}\mathcal{O}_{X^*\times S})\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S}))\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}(p_{X^*}^{-1}G\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S}))\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}p_{X^*}^{-1}G\otimes^L_{\rho_{S!}p_{X^*}^{-1}\mathcal{O}_S}\rho_{S!}\mathcal{O}_{X^*\times S})\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq \rho_{S*}p_{_X^{*}}^{-1}G\otimes^L_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S}. \end{align*}
\begin{align*} \rho_{S*}L\otimes^L_{\rho_{S*}p_{X*}^{-1}\mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S} &\simeq(\rho_{S!}L\otimes^L_{\rho_{S!}p_{X^*}^{-1}\mathcal{O}_S}\rho_{S!}\mathcal{O}_{X^*\times S})\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S}))\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}(p_{X^*}^{-1}G\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S}))\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq(\rho_{S!}p_{X^*}^{-1}G\otimes^L_{\rho_{S!}p_{X^*}^{-1}\mathcal{O}_S}\rho_{S!}\mathcal{O}_{X^*\times S})\otimes^L_{\rho_{S!}\mathcal{O}_{X^*\times S}}j^{-1}\mathcal{O}_{X\times S}^{t,S}\\ &\simeq \rho_{S*}p_{_X^{*}}^{-1}G\otimes^L_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S}j^{-1}\mathcal{O}_{X\times S}^{t,S}. \end{align*}
Then, due to (5.17), we deduce an ![]() $\mathcal {O}_{X\times S}$-linear isomorphism
$\mathcal {O}_{X\times S}$-linear isomorphism
By the first part of the proof, we deduce that ![]() $\widetilde E^S_L$ is concentrated in degree zero. This concludes the proof of Proposition 5.18.
$\widetilde E^S_L$ is concentrated in degree zero. This concludes the proof of Proposition 5.18.
Lemma 5.24 Both ![]() $\widetilde E_L$ and
$\widetilde E_L$ and ![]() $\widetilde E^S_L$ are naturally
$\widetilde E^S_L$ are naturally ![]() $\mathcal {D}_{X\times S/S}$-submodules of
$\mathcal {D}_{X\times S/S}$-submodules of ![]() $j_*E_L$.
$j_*E_L$.
Proof. First, applying the commutation of ![]() $\rho _{S}^{-1}$ with
$\rho _{S}^{-1}$ with ![]() $j^{-1}$ together with the analogue of [Reference Monteiro Fernandes and SabbahMFS19, Corollary 3.24] entails that
$j^{-1}$ together with the analogue of [Reference Monteiro Fernandes and SabbahMFS19, Corollary 3.24] entails that ![]() $\widetilde E^S_L$ and
$\widetilde E^S_L$ and ![]() $\widetilde E_L$ coincide with
$\widetilde E_L$ coincide with ![]() $E_L$ when restricted to
$E_L$ when restricted to ![]() $X^*\times S$.
$X^*\times S$.
On the one hand, by construction, ![]() $\widetilde E_L$ is naturally a
$\widetilde E_L$ is naturally a ![]() $\mathcal {D}_{X\times S/S}$-submodule of
$\mathcal {D}_{X\times S/S}$-submodule of ![]() $j_*E_L$. Let us check, on the other hand, that
$j_*E_L$. Let us check, on the other hand, that ![]() $\widetilde E^S_L$ is also naturally a
$\widetilde E^S_L$ is also naturally a ![]() $\mathcal {D}_{X\times S/S}$-submodule of
$\mathcal {D}_{X\times S/S}$-submodule of ![]() $j_*E_L$. From the natural morphism of functors
$j_*E_L$. From the natural morphism of functors ![]() $\operatorname {Id}\rightarrow R\rho _{S*}\rho _S^{-1}$ on
$\operatorname {Id}\rightarrow R\rho _{S*}\rho _S^{-1}$ on ![]() $\mathrm {Mod}(\mathbb {C}_{X_{\mathrm {sa}}\times S})$ we derive a natural morphism
$\mathrm {Mod}(\mathbb {C}_{X_{\mathrm {sa}}\times S})$ we derive a natural morphism ![]() $\rho _S^{-1}Rj_*\rightarrow Rj_*\rho _{S}^{-1}$: denoting for a moment by
$\rho _S^{-1}Rj_*\rightarrow Rj_*\rho _{S}^{-1}$: denoting for a moment by ![]() $j_*^S$ the morphism in the subanalytic site, we have an isomorphism of functors
$j_*^S$ the morphism in the subanalytic site, we have an isomorphism of functors ![]() $Rj_*^S\circ R\rho _{S*}\stackrel {\sim }{\longrightarrow } R\rho _{S*}\circ Rj_*$ (cf. [Reference PrelliPre08, Proposition 2.2.1(i)], by replacing there
$Rj_*^S\circ R\rho _{S*}\stackrel {\sim }{\longrightarrow } R\rho _{S*}\circ Rj_*$ (cf. [Reference PrelliPre08, Proposition 2.2.1(i)], by replacing there ![]() $\rho$ by
$\rho$ by ![]() $\rho _S$ and using the same argument), hence a morphism
$\rho _S$ and using the same argument), hence a morphism
and, by applying ![]() $\rho _S^{-1}$ on the left, we obtain the desired morphism. Recall also, as already used, that
$\rho _S^{-1}$ on the left, we obtain the desired morphism. Recall also, as already used, that ![]() $\rho _{S*}L\stackrel {\sim }{\longrightarrow } R\rho _{S*}L$. We then deduce a
$\rho _{S*}L\stackrel {\sim }{\longrightarrow } R\rho _{S*}L$. We then deduce a ![]() $\mathcal {D}_{X\times S/S}$-linear morphism
$\mathcal {D}_{X\times S/S}$-linear morphism
 \begin{align*} \Psi:\widetilde E^S_L&\simeq\rho_S^{-1}Rj_*(\rho_{S*}L \otimes^L_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\longrightarrow Rj_*\rho_{S}^{-1}(\rho_{S*}L\otimes^L_{\rho_{S*}p_{X*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\overset{{(a)}}\simeq Rj_*(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\rho_S^{-1} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\simeq Rj_*(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S})\\ &\overset{{(b)}}\simeq Rj_*(L\otimes_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S})=Rj_*E_L\overset{{(c)}}\simeq j_*E_L, \end{align*}
\begin{align*} \Psi:\widetilde E^S_L&\simeq\rho_S^{-1}Rj_*(\rho_{S*}L \otimes^L_{\rho_{S*}p_{X^*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\longrightarrow Rj_*\rho_{S}^{-1}(\rho_{S*}L\otimes^L_{\rho_{S*}p_{X*}^{-1}\mathcal{O}_S} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\overset{{(a)}}\simeq Rj_*(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\rho_S^{-1} j^{-1}\mathcal{O}^{t, S}_{X\times S})\\ &\simeq Rj_*(L\otimes^L_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S})\\ &\overset{{(b)}}\simeq Rj_*(L\otimes_{p_{X^*}^{-1}\mathcal{O}_S}\mathcal{O}_{X^*\times S})=Rj_*E_L\overset{{(c)}}\simeq j_*E_L, \end{align*}
where part (a) follows from (5.2), part (b) follows from the ![]() $p_{X^*}^{-1}\mathcal {O}_S$-flatness of
$p_{X^*}^{-1}\mathcal {O}_S$-flatness of ![]() $\mathcal {O}_{X^*\times S}$, and part (c) follows from the Steinness of
$\mathcal {O}_{X^*\times S}$, and part (c) follows from the Steinness of ![]() $j$.
$j$.
In order to check that ![]() $\Psi$ is injective, it is enough to consider it as an
$\Psi$ is injective, it is enough to consider it as an ![]() $\mathcal {O}_{X\times S}$-linear morphism, and by (5.23), it is enough to check injectivity when
$\mathcal {O}_{X\times S}$-linear morphism, and by (5.23), it is enough to check injectivity when ![]() $L=p_{X^*}^{-1}G$. Furthermore, the question is local on
$L=p_{X^*}^{-1}G$. Furthermore, the question is local on ![]() $S$.
$S$.
In such a case, we consider a resolution ![]() $\mathcal {O}_S^\bullet\rightarrow G$ as in the proof of Proposition 5.18. Then, locally on
$\mathcal {O}_S^\bullet\rightarrow G$ as in the proof of Proposition 5.18. Then, locally on ![]() $S$, (5.21) identifies
$S$, (5.21) identifies ![]() $\widetilde E^S_{p_{X^*}^{-1}G}$ with
$\widetilde E^S_{p_{X^*}^{-1}G}$ with ![]() $p_{X}^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S} \mathcal {O}_{X\times S}(*D)$ and the morphism
$p_{X}^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S} \mathcal {O}_{X\times S}(*D)$ and the morphism ![]() $\Psi$ with the natural morphism
$\Psi$ with the natural morphism
which is injective because ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-coherent, as desired.
$\mathcal {O}_S$-coherent, as desired.
End of the proof of Proposition 5.15. By Lemma 5.24, we are reduced to showing that both ![]() $\mathcal {D}_{X\times S/S}$-submodules
$\mathcal {D}_{X\times S/S}$-submodules ![]() $\widetilde E^S_L$ and
$\widetilde E^S_L$ and ![]() $\widetilde E_L$ of
$\widetilde E_L$ of ![]() $j_*E_L$ coincide, and because the
$j_*E_L$ coincide, and because the ![]() $\mathcal {D}_{X\times S/S}$-structure is induced by that
$\mathcal {D}_{X\times S/S}$-structure is induced by that ![]() $j_*E_L$ for both, it is enough to check that they coincide as
$j_*E_L$ for both, it is enough to check that they coincide as ![]() $\mathcal {O}_{X\times S}$-submodules. The question is local on
$\mathcal {O}_{X\times S}$-submodules. The question is local on ![]() $X\times S$. By Remark 4.18, there exists a local
$X\times S$. By Remark 4.18, there exists a local ![]() $\mathcal {O}_{X\times S}$-linear isomorphism
$\mathcal {O}_{X\times S}$-linear isomorphism ![]() $j_*E_L\simeq j_*\widehat E_{p_{X^*}^{-1}G}$ under which
$j_*E_L\simeq j_*\widehat E_{p_{X^*}^{-1}G}$ under which ![]() $\widetilde E_L$ is identified with
$\widetilde E_L$ is identified with ![]() $\widehat E_G=p_X^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S}\mathcal {O}_{X\times S}(*D)$. In addition, (5.23) also identifies
$\widehat E_G=p_X^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S}\mathcal {O}_{X\times S}(*D)$. In addition, (5.23) also identifies ![]() $\widetilde E^S_L$ with
$\widetilde E^S_L$ with ![]() $p_X^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S}\mathcal {O}_{X\times S}(*D)$ as an
$p_X^{-1}G\otimes _{p_X^{-1}\mathcal {O}_S}\mathcal {O}_{X\times S}(*D)$ as an ![]() $\mathcal {O}_{X\times S}$-module under the same local isomorphism, so the
$\mathcal {O}_{X\times S}$-module under the same local isomorphism, so the ![]() $\mathcal {O}_{X\times S}$-submodules
$\mathcal {O}_{X\times S}$-submodules ![]() $\widetilde E_L$ and
$\widetilde E_L$ and ![]() $\widetilde E^S_L$ of
$\widetilde E^S_L$ of ![]() $j_*E_L$ locally coincide, as desired.
$j_*E_L$ locally coincide, as desired.
6. Proof of Theorem 2
The proof of Theorem 2 is similar to that of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Theorem 1] where ![]() $\dim S=1$. However, various improvements are necessary in order to handle the case
$\dim S=1$. However, various improvements are necessary in order to handle the case ![]() $\dim S\geqslant 2$.
$\dim S\geqslant 2$.
6.a First part of the proof of Theorem 2
We prove that ![]() $\operatorname {RH}_X^S$ is a right quasi-inverse of the functor
$\operatorname {RH}_X^S$ is a right quasi-inverse of the functor ![]() $\operatorname {{}^\mathrm {p}Sol}_X:\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ by exhibiting an isomorphism of functors
$\operatorname {{}^\mathrm {p}Sol}_X:\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ by exhibiting an isomorphism of functors ![]() $\alpha :\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)}\stackrel {\sim }{\longrightarrow }\operatorname {{}^\mathrm {p}Sol}_X\circ \operatorname {RH}_X^S$. This is the analogue in possibly higher dimension for
$\alpha :\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)}\stackrel {\sim }{\longrightarrow }\operatorname {{}^\mathrm {p}Sol}_X\circ \operatorname {RH}_X^S$. This is the analogue in possibly higher dimension for ![]() $S$ of [Reference Monteiro Fernandes and SabbahMFS19, Theorem 3]:
$S$ of [Reference Monteiro Fernandes and SabbahMFS19, Theorem 3]:
(6.1) For
 $F$ in
$F$ in  $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$,
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$,  $\operatorname {RH}_X^S(F)$ is an object of
$\operatorname {RH}_X^S(F)$ is an object of  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ and there exists a functorial isomorphism
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ and there exists a functorial isomorphism  $\alpha _F:F\simeq \operatorname {{}^\mathrm {p}Sol}_X(\operatorname {RH}_X^S(F))$ in
$\alpha _F:F\simeq \operatorname {{}^\mathrm {p}Sol}_X(\operatorname {RH}_X^S(F))$ in  $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$.
Proof of (6.1) We recall the notation for the duality functor (cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.23]): for ![]() $F$ in
$F$ in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$, we set
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$, we set ![]() $\boldsymbol {D}'F=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$ and
$\boldsymbol {D}'F=R\mathcal {H}\!\mathit {om}_{p^{-1}\mathcal {O}_S}(F,p^{-1}\mathcal {O}_S)\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {R} {-c}}(p^{-1}\mathcal {O}_S)$ and ![]() $\boldsymbol {D} F=\boldsymbol {D}'F[2\dim X]$. Functoriality in (6.1) is obtained by means of Lemma 5.16: once we know that, for
$\boldsymbol {D} F=\boldsymbol {D}'F[2\dim X]$. Functoriality in (6.1) is obtained by means of Lemma 5.16: once we know that, for ![]() $F$ in
$F$ in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$,
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$, ![]() $\operatorname {RH}_X^S(F)$ belongs to
$\operatorname {RH}_X^S(F)$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, we can apply [Reference Monteiro Fernandes and SabbahMFS13, Corollary 3.9] together with bi-duality in
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, we can apply [Reference Monteiro Fernandes and SabbahMFS13, Corollary 3.9] together with bi-duality in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ (cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.23]) to obtain a functorial isomorphism
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ (cf. [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.23]) to obtain a functorial isomorphism
For the first part of (6.1), the main step is provided by Proposition 5.15, where we proved the case ![]() $F=j_!\boldsymbol {D}'L$ in the setting of § 4.b (from which we keep the notation), that is,
$F=j_!\boldsymbol {D}'L$ in the setting of § 4.b (from which we keep the notation), that is, ![]() $D$ is a normal crossing divisor in
$D$ is a normal crossing divisor in ![]() $X$ and
$X$ and ![]() $L$ is a coherent
$L$ is a coherent ![]() $S$-local system on
$S$-local system on ![]() $X^*\times S:=(X\smallsetminus D)\times S$.
$X^*\times S:=(X\smallsetminus D)\times S$.
We now conclude the proof of (6.1) by a standard induction on the dimension of the ![]() $X$-support of
$X$-support of ![]() $F$, based on Theorem 5.11, analogous to that of [Reference KashiwaraKas84, §7.3] (cf. [Reference Monteiro Fernandes and SabbahMFS19, Theorem 3] for the case
$F$, based on Theorem 5.11, analogous to that of [Reference KashiwaraKas84, §7.3] (cf. [Reference Monteiro Fernandes and SabbahMFS19, Theorem 3] for the case ![]() $\dim S=1$).
$\dim S=1$).
We thus assume that (6.1) holds if ![]() $\dim \operatorname {Supp}_XF< k$ (
$\dim \operatorname {Supp}_XF< k$ (![]() $k\geqslant 1$) and we prove that it holds for any
$k\geqslant 1$) and we prove that it holds for any ![]() $F$ with
$F$ with ![]() $\dim \operatorname {Supp}_XF\leqslant k$. By functoriality, it is enough to prove the first part of (6.1), so that the question is local. By induction on the amplitude of the complex
$\dim \operatorname {Supp}_XF\leqslant k$. By functoriality, it is enough to prove the first part of (6.1), so that the question is local. By induction on the amplitude of the complex ![]() $F$, we can also assume that
$F$, we can also assume that ![]() $F$ is an
$F$ is an ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible sheaf. We can find a projective morphism
$\mathbb {C}$-constructible sheaf. We can find a projective morphism ![]() $f:X'\rightarrow X$ with
$f:X'\rightarrow X$ with ![]() $\dim X'=k$, which is biholomorphic from the complement
$\dim X'=k$, which is biholomorphic from the complement ![]() $X^{\prime *}$ of a normal crossing divisor
$X^{\prime *}$ of a normal crossing divisor ![]() $D'$ in
$D'$ in ![]() $X'$ to the smooth locus of dimension
$X'$ to the smooth locus of dimension ![]() $k$ of
$k$ of ![]() $\operatorname {Supp}_XF$, so that
$\operatorname {Supp}_XF$, so that ![]() $f^{-1}F$ is a coherent
$f^{-1}F$ is a coherent ![]() $S$-local system on
$S$-local system on ![]() $X^{\prime *}$. Let
$X^{\prime *}$. Let ![]() $j':X^{\prime *}\mathrel {\hookrightarrow} X'$ denote the inclusion. Proposition 5.15 implies the regular holonomicity of
$j':X^{\prime *}\mathrel {\hookrightarrow} X'$ denote the inclusion. Proposition 5.15 implies the regular holonomicity of ![]() $\operatorname {RH}^S(j'_!\boldsymbol {D}'j^{\prime -1}f^{-1}F)$ and Theorem 5.11, together with [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.4], implies regular holonomicity of
$\operatorname {RH}^S(j'_!\boldsymbol {D}'j^{\prime -1}f^{-1}F)$ and Theorem 5.11, together with [Reference Monteiro Fernandes and SabbahMFS19, Corollary 2.4], implies regular holonomicity of
where ![]() $j$ denotes the inclusion of
$j$ denotes the inclusion of ![]() $f(X^{\prime *})$ in
$f(X^{\prime *})$ in ![]() $X$. Hence, if
$X$. Hence, if ![]() $F$ is an
$F$ is an ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible sheaf with
$\mathbb {C}$-constructible sheaf with ![]() $X$-support of dimension
$X$-support of dimension ![]() $\leqslant k$,
$\leqslant k$, ![]() $\operatorname {RH}_X^S(\boldsymbol {D}'F)$ is regular holonomic because it fits in a distinguished triangle whose third term is regular holonomic by the induction hypothesis. The same holds for
$\operatorname {RH}_X^S(\boldsymbol {D}'F)$ is regular holonomic because it fits in a distinguished triangle whose third term is regular holonomic by the induction hypothesis. The same holds for ![]() $\boldsymbol {D}'F$ for any
$\boldsymbol {D}'F$ for any ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ with
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ with ![]() $\dim \operatorname {Supp}_XF\leqslant k$, and replacing
$\dim \operatorname {Supp}_XF\leqslant k$, and replacing ![]() $F$ with
$F$ with ![]() $\boldsymbol {D}'F$, which has the same
$\boldsymbol {D}'F$, which has the same ![]() $X$-support, we conclude that
$X$-support, we conclude that ![]() $\operatorname {RH}_X^S(F)$ is regular holonomic.
$\operatorname {RH}_X^S(F)$ is regular holonomic.
6.b Second part of the proof of Theorem 2
We prove that ![]() $\operatorname {RH}_X^S$ is a left quasi-inverse of the functor
$\operatorname {RH}_X^S$ is a left quasi-inverse of the functor ![]() $\operatorname {{}^\mathrm {p}Sol}_X:\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ by exhibiting an isomorphism of functors
$\operatorname {{}^\mathrm {p}Sol}_X:\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$ by exhibiting an isomorphism of functors ![]() $\beta :\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})}\stackrel {\sim }{\longrightarrow }\operatorname {RH}_X^S\circ \operatorname {{}^\mathrm {p}Sol}_X$.
$\beta :\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})}\stackrel {\sim }{\longrightarrow }\operatorname {RH}_X^S\circ \operatorname {{}^\mathrm {p}Sol}_X$.
(6.2) For each object
 $\mathcal {M}$ of
$\mathcal {M}$ of  $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, there exists an isomorphism
functorial in
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$, there exists an isomorphism
functorial in \[ \beta_\mathcal{M}:\mathcal{M}\stackrel{\sim}{\longrightarrow}\operatorname{RH}_X^S(\operatorname{{}^\mathrm{p}Sol}_X(\mathcal{M})), \]
\[ \beta_\mathcal{M}:\mathcal{M}\stackrel{\sim}{\longrightarrow}\operatorname{RH}_X^S(\operatorname{{}^\mathrm{p}Sol}_X(\mathcal{M})), \]
 $\mathcal {M}$.
$\mathcal {M}$.
Proof of (6.2)
As in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, §3.b], we construct a bi-functorial isomorphism (with respect to ![]() $\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$) which, by applying
$\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$) which, by applying ![]() $Li^*_s$ for any
$Li^*_s$ for any ![]() $s\in S$, yields that of [Reference KashiwaraKas84, Corollary 8.6]:
$s\in S$, yields that of [Reference KashiwaraKas84, Corollary 8.6]:
that we also denote as ![]() $(6.3)_{\mathcal {M},\mathcal {N}}$. We then define the morphism
$(6.3)_{\mathcal {M},\mathcal {N}}$. We then define the morphism
as the unique morphism such that ![]() $(6.3)_{\mathcal {M},\mathcal {M}}(\beta _\mathcal {M})=\operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}(\mathcal {M})}$. One classically deduces from the full faithfulness of
$(6.3)_{\mathcal {M},\mathcal {M}}(\beta _\mathcal {M})=\operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}(\mathcal {M})}$. One classically deduces from the full faithfulness of ![]() $\operatorname {{}^\mathrm {p}Sol}$ in the absolute case (a consequence of the Riemann–Hilbert correspondence of [Reference KashiwaraKas84] and [Reference MebkhoutMeb84]) that, for each
$\operatorname {{}^\mathrm {p}Sol}$ in the absolute case (a consequence of the Riemann–Hilbert correspondence of [Reference KashiwaraKas84] and [Reference MebkhoutMeb84]) that, for each ![]() $s\in S$,
$s\in S$, ![]() $\beta _{Li^*_s\mathcal {M}}$ is an isomorphism. Therefore, by a Nakayama-type argument [Reference Monteiro Fernandes and SabbahMFS19, Proposition 1.9 and Corollary 1.10],
$\beta _{Li^*_s\mathcal {M}}$ is an isomorphism. Therefore, by a Nakayama-type argument [Reference Monteiro Fernandes and SabbahMFS19, Proposition 1.9 and Corollary 1.10], ![]() $\beta _{\mathcal {M}}$ is an isomorphism.
$\beta _{\mathcal {M}}$ is an isomorphism.
In order to check that ![]() $\beta _\mathcal {M}$ is functorial with respect to
$\beta _\mathcal {M}$ is functorial with respect to ![]() $\mathcal {M}$, that is, it defines a morphism of functors
$\mathcal {M}$, that is, it defines a morphism of functors ![]() $\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})}\rightarrow \operatorname {RH}^S_X\circ \operatorname {{}^\mathrm {p}Sol}_X$, we consider as in [Reference Monteiro Fernandes and SabbahMFS19, p. 668], for a morphism
$\operatorname {Id}_{\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})}\rightarrow \operatorname {RH}^S_X\circ \operatorname {{}^\mathrm {p}Sol}_X$, we consider as in [Reference Monteiro Fernandes and SabbahMFS19, p. 668], for a morphism ![]() $\varphi :\mathcal {M}\rightarrow \mathcal {N}$, the following commutative diagram.
$\varphi :\mathcal {M}\rightarrow \mathcal {N}$, the following commutative diagram.

As ![]() $\operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {M})}\circ \operatorname {{}^\mathrm {p}Sol}_X(\varphi )=\operatorname {{}^\mathrm {p}Sol}_X(\varphi )\circ \operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N})}$, we obtain from the commutativity of the diagram that
$\operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {M})}\circ \operatorname {{}^\mathrm {p}Sol}_X(\varphi )=\operatorname {{}^\mathrm {p}Sol}_X(\varphi )\circ \operatorname {Id}_{\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N})}$, we obtain from the commutativity of the diagram that
which is the desired functoriality.
In order to obtain (6.3), it is enough to construct a bi-functorial morphism in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$
$\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$
for ![]() $\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ and
$\mathcal {M}\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$ and ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, and to show that it is an isomorphism. Then
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, and to show that it is an isomorphism. Then ![]() $(6.3)_{\mathcal {M},\mathcal {N}}$ is obtained by taking global sections of
$(6.3)_{\mathcal {M},\mathcal {N}}$ is obtained by taking global sections of ![]() $\mathcal {H}^0 (6.4)$ applied to
$\mathcal {H}^0 (6.4)$ applied to ![]() $F=\operatorname {{}^\mathrm {p}Sol}(\mathcal {N})$.
$F=\operatorname {{}^\mathrm {p}Sol}(\mathcal {N})$.
Such a morphism (6.4) is given by [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, (14)]. In view of Proposition 5.9 we can argue as in [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21], where it is also shown that, for each ![]() $s_o\in S$,
$s_o\in S$, ![]() $Li_{s_o}^* (6.4)$ can be identified with the morphism constructed in the absolute case by Kashiwara [Reference KashiwaraKas84, Corollary 8.6], hence it is an isomorphism. To conclude that (6.4) is an isomorphism, we apply a Nakayama-type argument [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.2].
$Li_{s_o}^* (6.4)$ can be identified with the morphism constructed in the absolute case by Kashiwara [Reference KashiwaraKas84, Corollary 8.6], hence it is an isomorphism. To conclude that (6.4) is an isomorphism, we apply a Nakayama-type argument [Reference Monteiro Fernandes and SabbahMFS13, Proposition 2.2].
To construct the morphism (6.4) we need to check a finiteness property. The proof of (6.2) is thus concluded with the proof of the following assertion.
(6.5) For any
 $\mathcal {M} \in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and for any
$\mathcal {M} \in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and for any  $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$,
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathbb {C} {-c}}(p^{-1}\mathcal {O}_S)$,  $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \operatorname {RH}^S_X(F))$ belongs to
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \operatorname {RH}^S_X(F))$ belongs to  $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
We also consider the following statement.
(6.6) For any
 $\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, the complex
$\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$, the complex  $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$ belongs to
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$ belongs to  $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
We argue by induction on the pair ![]() $(\dim S,\dim \operatorname {Supp}_X\mathcal {M})$ ordered lexicographically. For that purpose we introduce the following notation.
$(\dim S,\dim \operatorname {Supp}_X\mathcal {M})$ ordered lexicographically. For that purpose we introduce the following notation.
• For
 $d\geqslant 0$, we denote by
$d\geqslant 0$, we denote by  $6.5)_d$, respectively,
$6.5)_d$, respectively,  $\textrm{(6.6)}_d$, the corresponding statement concerning any
$\textrm{(6.6)}_d$, the corresponding statement concerning any  $S$ satisfying
$S$ satisfying  $\dim S\leqslant d$.
$\dim S\leqslant d$.• For
 $k\geqslant 0$, we introduce the assertion
$k\geqslant 0$, we introduce the assertion  $\textrm{(6.6)}_{d,k}$ by requiring that the property holds for
$\textrm{(6.6)}_{d,k}$ by requiring that the property holds for  $\dim S \leqslant d-1$ or
$\dim S \leqslant d-1$ or  $\dim S = d$ and
$\dim S = d$ and  $\dim \operatorname {Supp}_X\mathcal {M} \leqslant k$.
$\dim \operatorname {Supp}_X\mathcal {M} \leqslant k$.
Because of the first part of (6.1) already proved, we have
Conversely, the reverse implication also holds:
Indeed we deduce from ![]() $\text{(6.5)}_d$ an isomorphism
$\text{(6.5)}_d$ an isomorphism ![]() $\beta _\mathcal {N}:\mathcal {N}\stackrel {\sim }{\longrightarrow }\operatorname {RH}^S_X(\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N}))$, so applying
$\beta _\mathcal {N}:\mathcal {N}\stackrel {\sim }{\longrightarrow }\operatorname {RH}^S_X(\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N}))$, so applying ![]() $\text{({6.5})}_d$ with
$\text{({6.5})}_d$ with ![]() $F=\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N})$ gives
$F=\operatorname {{}^\mathrm {p}Sol}_X(\mathcal {N})$ gives ![]() $\textrm{(6.6)}_d$. In the following, we focus on
$\textrm{(6.6)}_d$. In the following, we focus on ![]() $\textrm{(6.6)}_d$. As belonging to
$\textrm{(6.6)}_d$. As belonging to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ is a local property (cf. [Reference Monteiro Fernandes and SabbahMFS13, §2.5]), we allow restriction to an open neighborhood of a point of
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ is a local property (cf. [Reference Monteiro Fernandes and SabbahMFS13, §2.5]), we allow restriction to an open neighborhood of a point of ![]() $X\times S$ when needed.
$X\times S$ when needed.
Proof Proof of  $\textrm{(6.6)}_d$
$\textrm{(6.6)}_d$
The proof of ![]() $\textrm{(6.6)}_d$ is done by induction on
$\textrm{(6.6)}_d$ is done by induction on ![]() $d$, in order to reduce the assertion to the particular case of Lemma 6.15. Let us recall that
$d$, in order to reduce the assertion to the particular case of Lemma 6.15. Let us recall that ![]() $\textrm{(6.6)}_0$ holds, according to [Reference KashiwaraKas84]. Thus, we assume that
$\textrm{(6.6)}_0$ holds, according to [Reference KashiwaraKas84]. Thus, we assume that ![]() $\textrm{(6.6)}_{d-1}$ holds (
$\textrm{(6.6)}_{d-1}$ holds (![]() $d\geqslant 1$) and we consider
$d\geqslant 1$) and we consider ![]() $S$ with
$S$ with ![]() $\dim S=d$, together with any
$\dim S=d$, together with any ![]() $\mathcal {M},\mathcal {N} \in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$.
$\mathcal {M},\mathcal {N} \in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$.
Step 1: the ![]() $S$-torsion case.
$S$-torsion case.
Lemma 6.7 Let ![]() $\dim S=d$ and let us assume that
$\dim S=d$ and let us assume that ![]() $\textrm{(6.6)}_{d-1}$ holds. Let
$\textrm{(6.6)}_{d-1}$ holds. Let ![]() $\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and assume that the cohomology of
$\mathcal {M},\mathcal {N}\in \operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ and assume that the cohomology of ![]() $\mathcal {M}$ or that of
$\mathcal {M}$ or that of ![]() $\mathcal {N}$ is of
$\mathcal {N}$ is of ![]() $S$-torsion. Then
$S$-torsion. Then ![]() $\textrm{(6.6)}_d$ holds for
$\textrm{(6.6)}_d$ holds for ![]() $\mathcal {M},\mathcal {N}$, that is,
$\mathcal {M},\mathcal {N}$, that is,
Proof. By the biduality isomorphism of [Reference Monteiro Fernandes and SabbahMFS13, (3)], we have
and we recall that both ![]() $\boldsymbol {D}\mathcal {N}$ and
$\boldsymbol {D}\mathcal {N}$ and ![]() $\boldsymbol {D}\mathcal {M}$ are regular holonomic according to Corollary 3.9. It is thus enough to prove Lemma 6.7 when the cohomology of
$\boldsymbol {D}\mathcal {M}$ are regular holonomic according to Corollary 3.9. It is thus enough to prove Lemma 6.7 when the cohomology of ![]() $\mathcal {N}$ is of
$\mathcal {N}$ is of ![]() $S$-torsion. On the other hand, owing to the definition of
$S$-torsion. On the other hand, owing to the definition of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ in terms of micro-support (cf. [Reference Monteiro Fernandes and SabbahMFS13, §2.5]), if two terms of a distinguished triangle in
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ in terms of micro-support (cf. [Reference Monteiro Fernandes and SabbahMFS13, §2.5]), if two terms of a distinguished triangle in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$ are objects of
$\operatorname {\mathsf {D}}^\mathrm {b}(p^{-1}\mathcal {O}_S)$ are objects of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, then so does the third. This property allows us to assume that
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, then so does the third. This property allows us to assume that ![]() $\mathcal {M},\mathcal {N}$ are regular holonomic
$\mathcal {M},\mathcal {N}$ are regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules instead of complexes. Lastly, the same argument implies that belonging to
$\mathcal {D}_{X\times S/S}$-modules instead of complexes. Lastly, the same argument implies that belonging to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ is a local question on
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ is a local question on ![]() $X\times S$.
$X\times S$.
The assumption on ![]() $\mathcal {N}$ entails that
$\mathcal {N}$ entails that ![]() $\operatorname {Supp}_S \mathcal {N}$ is, locally with respect to
$\operatorname {Supp}_S \mathcal {N}$ is, locally with respect to ![]() ${X\times S}$, contained in a closed analytic subset
${X\times S}$, contained in a closed analytic subset ![]() $T$ of
$T$ of ![]() $S$ such that
$S$ such that ![]() $\dim T<\dim S$. We argue by induction on
$\dim T<\dim S$. We argue by induction on ![]() $\dim T$.
$\dim T$.
If ![]() $\dim T=0$, as we consider a local situation, we may assume
$\dim T=0$, as we consider a local situation, we may assume ![]() $T=\{s_o\}$ with maximal ideal sheaf
$T=\{s_o\}$ with maximal ideal sheaf ![]() $\mathfrak {m}_{s_o}$. By considering the (locally) finite filtration of
$\mathfrak {m}_{s_o}$. By considering the (locally) finite filtration of ![]() $\mathcal {N}$ by the
$\mathcal {N}$ by the ![]() $\mathcal {D}_{X\times S/S}$-regular holonomic submodules
$\mathcal {D}_{X\times S/S}$-regular holonomic submodules ![]() $\mathfrak {m}_{s_o}^k\mathcal {N}$ (
$\mathfrak {m}_{s_o}^k\mathcal {N}$ (![]() $k\in \mathbb {N}$), we may reduce to assume
$k\in \mathbb {N}$), we may reduce to assume ![]() $\mathfrak {m}_{s_o}\mathcal {N}=0$. We then have
$\mathfrak {m}_{s_o}\mathcal {N}=0$. We then have ![]() $\mathcal {N}\simeq i_{s_0 *} i^*_{s_0}\mathcal {N}$ and, by adjunction,
$\mathcal {N}\simeq i_{s_0 *} i^*_{s_0}\mathcal {N}$ and, by adjunction,
so that the proof is reduced to applying ![]() $\textrm{(6.6)}_0$ or, equivalently, the absolute case proved by Kashiwara in [Reference KashiwaraKas84].
$\textrm{(6.6)}_0$ or, equivalently, the absolute case proved by Kashiwara in [Reference KashiwaraKas84].
Assume now that ![]() $\dim T\geqslant 1$ and let
$\dim T\geqslant 1$ and let ![]() $T_0\subset T$ be a closed analytic subset of dimension
$T_0\subset T$ be a closed analytic subset of dimension ![]() $<\dim T$ such that
$<\dim T$ such that ![]() $T\smallsetminus T_0$ is non-singular of dimension
$T\smallsetminus T_0$ is non-singular of dimension ![]() $\dim T$. Let
$\dim T$. Let ![]() $\pi : S'\rightarrow S$ be a projective morphism of complex manifolds satisfying the two conditions:
$\pi : S'\rightarrow S$ be a projective morphism of complex manifolds satisfying the two conditions: ![]() $\pi (S')=T$ and, setting
$\pi (S')=T$ and, setting ![]() $T'_0:=\pi ^{-1}(T_0)$,
$T'_0:=\pi ^{-1}(T_0)$, ![]() $\pi ':=\pi |_{S'\smallsetminus T'_0}: S'\smallsetminus T'_0\rightarrow T\smallsetminus T_0$ is a biholomorphism. In particular,
$\pi ':=\pi |_{S'\smallsetminus T'_0}: S'\smallsetminus T'_0\rightarrow T\smallsetminus T_0$ is a biholomorphism. In particular, ![]() $\dim S'=\dim T< d$.
$\dim S'=\dim T< d$.
Note that, according to Proposition 3.10, ![]() $L\pi ^{*}\mathcal {M}$,
$L\pi ^{*}\mathcal {M}$, ![]() $L\pi ^{*}\mathcal {N}$ are regular holonomic on
$L\pi ^{*}\mathcal {N}$ are regular holonomic on ![]() $X\times S'$ and, by Theorem 3.15,
$X\times S'$ and, by Theorem 3.15, ![]() $R\pi _*L\pi ^*\mathcal {N}$ belongs to
$R\pi _*L\pi ^*\mathcal {N}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$. By
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {rhol}(\mathcal {D}_{X\times S/S})$. By ![]() $\textrm{(6.6)}_{d-1}$,
$\textrm{(6.6)}_{d-1}$, ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S'/S'}}( L\pi ^*\mathcal {M}, L\pi ^{*}\mathcal {N})\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{\prime -1}\mathcal {O}_{S'})$ thus, by the properness of
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S'/S'}}( L\pi ^*\mathcal {M}, L\pi ^{*}\mathcal {N})\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{\prime -1}\mathcal {O}_{S'})$ thus, by the properness of ![]() $\pi$ and Lemma 2.16,
$\pi$ and Lemma 2.16,
The cones of the natural morphisms ![]() $R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ and
$R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ and ![]() $\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ are supported in
$\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ are supported in ![]() $T_0$, so that, by the induction hypothesis, we deduce that
$T_0$, so that, by the induction hypothesis, we deduce that
and thus
Step 2: induction on ![]() $\dim \operatorname {Supp}_X\mathcal {M}$.
$\dim \operatorname {Supp}_X\mathcal {M}$.
Lemma 6.9 Let ![]() $\dim S=d\geqslant 1$ and let us assume that
$\dim S=d\geqslant 1$ and let us assume that ![]() $\textrm{(6.6)}_{d-1}$ holds. Then
$\textrm{(6.6)}_{d-1}$ holds. Then ![]() $\textrm{(6.6)}_{d,0}$ holds.
$\textrm{(6.6)}_{d,0}$ holds.
Proof. This is a consequence of Theorem 1 and adjunction. Indeed, we can assume that ![]() $\operatorname {Supp}_X\mathcal {M}=\{x\}$. Denoting the inclusion by
$\operatorname {Supp}_X\mathcal {M}=\{x\}$. Denoting the inclusion by ![]() $i:\{x\}\times S\mathrel {\hookrightarrow} X\times S$, there exists a coherent
$i:\{x\}\times S\mathrel {\hookrightarrow} X\times S$, there exists a coherent ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $\mathcal {M}_0$ such that
$\mathcal {M}_0$ such that ![]() $\mathcal {M}={}_{\scriptscriptstyle \mathrm {D}}i_*\mathcal {M}_0$ by Kashiwara's equivalence, and we have (cf. [Reference KashiwaraKas03, Theorem 4.33], which can be proved in a simple way in the present setting)
$\mathcal {M}={}_{\scriptscriptstyle \mathrm {D}}i_*\mathcal {M}_0$ by Kashiwara's equivalence, and we have (cf. [Reference KashiwaraKas03, Theorem 4.33], which can be proved in a simple way in the present setting)
By Theorem 1, ![]() ${}_{\scriptscriptstyle \mathrm {D}}i^*\mathcal {N}$ has
${}_{\scriptscriptstyle \mathrm {D}}i^*\mathcal {N}$ has ![]() $\mathcal {O}_S$-coherent cohomology, and the assertion follows.
$\mathcal {O}_S$-coherent cohomology, and the assertion follows.
We are thus reduced to proving the following.
(6.10) Let
 $\dim S=d\geqslant 1$. Assume that
$\dim S=d\geqslant 1$. Assume that  $\textrm{ (6.6)}_{d,k-1}$ holds (with
$\textrm{ (6.6)}_{d,k-1}$ holds (with  $k\geqslant 1$). Then
$k\geqslant 1$). Then  $\textrm{ (6.6)}_{d,k}$ holds.
$\textrm{ (6.6)}_{d,k}$ holds.
We can reduce to the case ![]() $\mathcal {M},\mathcal {N}$ are regular holonomic
$\mathcal {M},\mathcal {N}$ are regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules. Let
$\mathcal {D}_{X\times S/S}$-modules. Let ![]() $Z$ denote the
$Z$ denote the ![]() $X$-support of
$X$-support of ![]() $\mathcal {M}$. As the assertion is local, we can assume that there exists a hypersurface
$\mathcal {M}$. As the assertion is local, we can assume that there exists a hypersurface ![]() $Y$ of
$Y$ of ![]() $X$ such that
$X$ such that ![]() $Y$ contains the singular locus of
$Y$ contains the singular locus of ![]() $Z$ and
$Z$ and ![]() $\dim Z\cap Y< k$. Recall that localization along
$\dim Z\cap Y< k$. Recall that localization along ![]() $Y\times S$ preserves regular holonomicity (cf. Corollary 4.31).
$Y\times S$ preserves regular holonomicity (cf. Corollary 4.31).
Lemma 6.11 It is enough to prove the assertion (6.10) for ![]() $\mathcal {M},\mathcal {N}$ such that
$\mathcal {M},\mathcal {N}$ such that ![]() $\mathcal {M}=\mathcal {M}(*Y)$ and
$\mathcal {M}=\mathcal {M}(*Y)$ and ![]() $\mathcal {N}=\mathcal {N}(*Y)$.
$\mathcal {N}=\mathcal {N}(*Y)$.
Proof. The assertion for ![]() $\mathcal {M}$ follows from the property that
$\mathcal {M}$ follows from the property that ![]() $R\Gamma _{[Y]}\mathcal {M}$ belongs to
$R\Gamma _{[Y]}\mathcal {M}$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ (Corollary 4.32) and has
$\operatorname {\mathsf {D}}^\mathrm {b}_{\mathrm {rhol}}(\mathcal {D}_{X\times S/S})$ (Corollary 4.32) and has ![]() $X$-support of dimension
$X$-support of dimension ![]() $< k$.
$< k$.
For the assertion concerning ![]() $\mathcal {N}$, we recall the argument given at the end of the proof of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Theorem 3]. It is enough to prove that (6.10) holds if
$\mathcal {N}$, we recall the argument given at the end of the proof of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Theorem 3]. It is enough to prove that (6.10) holds if ![]() $\mathcal {N}=R\Gamma _{[Y]}\mathcal {N}$. We have, by [Reference Monteiro Fernandes and SabbahMFS13, (3)],
$\mathcal {N}=R\Gamma _{[Y]}\mathcal {N}$. We have, by [Reference Monteiro Fernandes and SabbahMFS13, (3)],
As ![]() $\mathcal {N}$ has
$\mathcal {N}$ has ![]() $\mathcal {D}_{X\times S/S}$-coherent cohomology and is supported on
$\mathcal {D}_{X\times S/S}$-coherent cohomology and is supported on ![]() $Y\times S$, we have
$Y\times S$, we have
Furthermore, ![]() $\boldsymbol {D}\mathcal {M}$ being regular holonomic, so is
$\boldsymbol {D}\mathcal {M}$ being regular holonomic, so is ![]() $R\Gamma _{[Y]}(\boldsymbol {D}\mathcal {M})$ by Corollary 4.32, as well as
$R\Gamma _{[Y]}(\boldsymbol {D}\mathcal {M})$ by Corollary 4.32, as well as ![]() $\mathcal {M}':=\boldsymbol {D} R\Gamma _{[Y]}(\boldsymbol {D}\mathcal {M})$. Finally, applying once more [Reference Monteiro Fernandes and SabbahMFS13, (3) and (1)], we obtain
$\mathcal {M}':=\boldsymbol {D} R\Gamma _{[Y]}(\boldsymbol {D}\mathcal {M})$. Finally, applying once more [Reference Monteiro Fernandes and SabbahMFS13, (3) and (1)], we obtain
with ![]() $\dim \operatorname {Supp}_X\mathcal {H}^j\mathcal {M}'< k$ for any
$\dim \operatorname {Supp}_X\mathcal {H}^j\mathcal {M}'< k$ for any ![]() $j$, so the latter complex is
$j$, so the latter complex is ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible by
$\mathbb {C}$-constructible by ![]() $\textrm{ (6.6)}_{d,k-1}$.
$\textrm{ (6.6)}_{d,k-1}$.
Step 3: reduction to the case where ![]() $\mathcal {M}$ is of D-type. We take up the notation of the proof of Proposition 4.27, so that
$\mathcal {M}$ is of D-type. We take up the notation of the proof of Proposition 4.27, so that ![]() $f:X'\rightarrow X$ is a projective morphism inducing a biholomorphism
$f:X'\rightarrow X$ is a projective morphism inducing a biholomorphism ![]() $X'\smallsetminus D\stackrel {\sim }{\longrightarrow } Z\smallsetminus Z\cap Y$, and we set
$X'\smallsetminus D\stackrel {\sim }{\longrightarrow } Z\smallsetminus Z\cap Y$, and we set ![]() $\delta =\dim X'-\dim X$.
$\delta =\dim X'-\dim X$.
Lemma 6.12 Let ![]() $\mathcal {M},\mathcal {N}$ be regular holonomic
$\mathcal {M},\mathcal {N}$ be regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules such that
$\mathcal {D}_{X\times S/S}$-modules such that ![]() $\mathcal {M}=\mathcal {M}(*Y)$. Then
$\mathcal {M}=\mathcal {M}(*Y)$. Then
Proof. There is a natural morphism of adjunction (cf. [Reference KashiwaraKas03, Theorem 4.33(1)])
We note that ![]() ${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M},{}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {N}$ are
${}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M},{}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {N}$ are ![]() $f$-good. Therefore, this morphism is a quasi-isomorphism. Furthermore, the natural adjunction morphism
$f$-good. Therefore, this morphism is a quasi-isomorphism. Furthermore, the natural adjunction morphism ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_*{}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}[\delta ]\rightarrow \mathcal {M}$ already used in the proof of Proposition 4.27 is an isomorphism if
${}_{\scriptscriptstyle \mathrm {D}}f_*{}_{\scriptscriptstyle \mathrm {D}}f^*\mathcal {M}[\delta ]\rightarrow \mathcal {M}$ already used in the proof of Proposition 4.27 is an isomorphism if ![]() $\mathcal {M}=\mathcal {M}(*Y)$.
$\mathcal {M}=\mathcal {M}(*Y)$.
Step 4: the case where ![]() $\mathcal {M}$ is of D-type along a normal crossing divisor. Recall Definition 4.23 and Proposition 4.26. From step 3, we are reduced to proving (6.10) in the following setting.
$\mathcal {M}$ is of D-type along a normal crossing divisor. Recall Definition 4.23 and Proposition 4.26. From step 3, we are reduced to proving (6.10) in the following setting.
(6.13) We have
 $\dim S=d$,
$\dim S=d$,  $\dim X=k$,
$\dim X=k$,  $\mathcal {M}{}\simeq \widetilde E_L$ is of D-type along a normal crossing divisor
$\mathcal {M}{}\simeq \widetilde E_L$ is of D-type along a normal crossing divisor  $D\subset X$, and
$D\subset X$, and  $\mathcal {N}=\mathcal {N}(*D)$.
$\mathcal {N}=\mathcal {N}(*D)$.
As the assertion is local, we can assume that ![]() $(E_L,\nabla )=(\widehat E_{G|X^*\times S},\widehat \nabla )$ as in (4.17) for some
$(E_L,\nabla )=(\widehat E_{G|X^*\times S},\widehat \nabla )$ as in (4.17) for some ![]() $\mathcal {O}_S$-coherent module
$\mathcal {O}_S$-coherent module ![]() $G$. We denote by
$G$. We denote by ![]() $r \geqslant 0$ the generic rank of
$r \geqslant 0$ the generic rank of ![]() $G$ as an
$G$ as an ![]() $\mathcal {O}_S$-module. The case
$\mathcal {O}_S$-module. The case ![]() $r=0$ means that
$r=0$ means that ![]() $G$ is a torsion
$G$ is a torsion ![]() $\mathcal {O}_S$-module.
$\mathcal {O}_S$-module.
Let us consider ![]() $X,S,D$ with
$X,S,D$ with ![]() $\dim S=d \geqslant 1$,
$\dim S=d \geqslant 1$, ![]() $\dim X=k \geqslant 1$ and
$\dim X=k \geqslant 1$ and ![]() $D$ is a divisor with normal crossings in
$D$ is a divisor with normal crossings in ![]() $X$. We argue by induction on
$X$. We argue by induction on ![]() $r$. For that purpose we consider, for
$r$. For that purpose we consider, for ![]() $r \geqslant 0$, the following assertion.
$r \geqslant 0$, the following assertion.
 $\textrm{ (6.6)}_{d,k,r}$d,k,r For any such
$\textrm{ (6.6)}_{d,k,r}$d,k,r For any such  $X,S,D$, the property
$X,S,D$, the property  $\textrm{ (6.6)}_{d,k-1}$ holds, as well as
$\textrm{ (6.6)}_{d,k-1}$ holds, as well as  $\textrm{ (6.6)}_{d,k}$ if
$\textrm{ (6.6)}_{d,k}$ if  $\mathcal {M}$ is of D-type with
$\mathcal {M}$ is of D-type with  $E_L=\widehat E_{G|X^*\times S}$ and
$E_L=\widehat E_{G|X^*\times S}$ and  $G$ being
$G$ being  $\mathcal {O}_S$-coherent of generic rank
$\mathcal {O}_S$-coherent of generic rank  $\leqslant r$, and
$\leqslant r$, and  $\mathcal {N}$ being regular holonomic satisfying
$\mathcal {N}$ being regular holonomic satisfying  $\mathcal {N}=\mathcal {N}(*D)$.
$\mathcal {N}=\mathcal {N}(*D)$.
Then, proving (6.13) amounts to proving ![]() $\textrm{ (6.6)}_{d,k,r}$ for any
$\textrm{ (6.6)}_{d,k,r}$ for any ![]() $r \geqslant 0$, according to Lemma 6.11.
$r \geqslant 0$, according to Lemma 6.11.
Lemma 6.14 If ![]() $\textrm{ (6.6)}_{d-1}$ holds, then:
$\textrm{ (6.6)}_{d-1}$ holds, then:
(i)
 $\textrm{ (6.6)}_{d,k,0}$ holds;
$\textrm{ (6.6)}_{d,k,0}$ holds;(ii) if
 $r\geqslant 1$ and if
$r\geqslant 1$ and if  $\textrm{ (6.6)}_{d,k,r}$ holds for any
$\textrm{ (6.6)}_{d,k,r}$ holds for any  $G$ which is
$G$ which is  $\mathcal {O}_S$-locally free and any
$\mathcal {O}_S$-locally free and any  $\mathcal {N}=\mathcal {N}(*D)$, then
$\mathcal {N}=\mathcal {N}(*D)$, then  $\textrm{ (6.6)}_{d,k,r}$ holds.
$\textrm{ (6.6)}_{d,k,r}$ holds.
Proof. The first point follows from Lemma 6.7. In order to prove the second point, we choose (locally on ![]() $S$) a projective modification
$S$) a projective modification ![]() $\pi :S'\rightarrow S$ as in Proposition 4.16. As the cones of the natural morphisms
$\pi :S'\rightarrow S$ as in Proposition 4.16. As the cones of the natural morphisms ![]() $\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ and
$\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ and ![]() $R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ are S-supported in dimension
$R\pi _*L\pi ^*\mathcal {N}\rightarrow R\pi _*\pi ^*\mathcal {N}$ are S-supported in dimension ![]() $< d$, Lemmas 6.7 and 2.16 imply that (6.6) holds for
$< d$, Lemmas 6.7 and 2.16 imply that (6.6) holds for ![]() $\mathcal {M},\mathcal {N}$ on
$\mathcal {M},\mathcal {N}$ on ![]() $X\times S$ if it holds for
$X\times S$ if it holds for ![]() $L\pi ^*\mathcal {M},L\pi ^*\mathcal {N}$ on
$L\pi ^*\mathcal {M},L\pi ^*\mathcal {N}$ on ![]() $X\times S'$. Furthermore,
$X\times S'$. Furthermore, ![]() $L^j\pi ^*\mathcal {M},L^j\pi ^*\mathcal {N}$ are also
$L^j\pi ^*\mathcal {M},L^j\pi ^*\mathcal {N}$ are also ![]() $S'$-supported in dimension
$S'$-supported in dimension ![]() $< d$ if
$< d$ if ![]() $j\neq 0$, so, by the same argument, (6.6) holds for
$j\neq 0$, so, by the same argument, (6.6) holds for ![]() $\mathcal {M},\mathcal {N}$ if it holds
$\mathcal {M},\mathcal {N}$ if it holds ![]() $\pi ^*\mathcal {M}$ and
$\pi ^*\mathcal {M}$ and ![]() $\pi ^*\mathcal {N}$. Lastly, by Lemma 6.7, we can replace
$\pi ^*\mathcal {N}$. Lastly, by Lemma 6.7, we can replace ![]() $\pi ^*\mathcal {M}$ and
$\pi ^*\mathcal {M}$ and ![]() $\pi ^*\mathcal {N}$ with their quotient
$\pi ^*\mathcal {N}$ with their quotient ![]() $\mathcal {M}',\mathcal {N}'$ by their
$\mathcal {M}',\mathcal {N}'$ by their ![]() $S'$-torsion subsheaves. Note that we still have
$S'$-torsion subsheaves. Note that we still have ![]() $\mathcal {N}'=\mathcal {N}'(*D)$ and
$\mathcal {N}'=\mathcal {N}'(*D)$ and ![]() $\mathcal {M}'$ is of D-type with corresponding
$\mathcal {M}'$ is of D-type with corresponding ![]() $E_{L'}$ isomorphic to
$E_{L'}$ isomorphic to ![]() $\widehat E_{G'|X^*\times S'}$, where
$\widehat E_{G'|X^*\times S'}$, where ![]() $G'$ is
$G'$ is ![]() $p^{\prime -1}\mathcal {O}_{S'}$-locally free by the choice of
$p^{\prime -1}\mathcal {O}_{S'}$-locally free by the choice of ![]() $\pi$. The assumption in point (ii) therefore implies that
$\pi$. The assumption in point (ii) therefore implies that ![]() $\textrm{ (6.6)}$ holds for any
$\textrm{ (6.6)}$ holds for any ![]() $G$ of generic rank
$G$ of generic rank ![]() $r$, as desired.
$r$, as desired.
Step 5: induction on the generic rank of ![]() $\mathcal {M}$. We use the same notation as in step 4 of the proof of Theorem 4.15.
$\mathcal {M}$. We use the same notation as in step 4 of the proof of Theorem 4.15.
Lemma 6.15 Assume that ![]() $\textrm{ (6.6)}_{d,k-1}$ holds. Then
$\textrm{ (6.6)}_{d,k-1}$ holds. Then ![]() $\textrm{ (6.6)}_{d,k,1}$ holds.
$\textrm{ (6.6)}_{d,k,1}$ holds.
Proof. Assume ![]() $\mathcal {M}$ is of D-type with
$\mathcal {M}$ is of D-type with ![]() $E_L=\widehat E_{G|X^*\times S}$ and
$E_L=\widehat E_{G|X^*\times S}$ and ![]() $G$ being
$G$ being ![]() $\mathcal {O}_S$-coherent and of generic rank one, and let
$\mathcal {O}_S$-coherent and of generic rank one, and let ![]() $\mathcal {N}$ be regular holonomic with
$\mathcal {N}$ be regular holonomic with ![]() $\mathcal {N}=\mathcal {N}(*D)$. By a projective modification we can assume that
$\mathcal {N}=\mathcal {N}(*D)$. By a projective modification we can assume that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free of rank one. Then, by Proposition 4.25(i), we have
$\mathcal {O}_S$-locally free of rank one. Then, by Proposition 4.25(i), we have ![]() $\mathcal {M}=\widehat E_G$.
$\mathcal {M}=\widehat E_G$.
The matrix of the relative connection ![]() $\widehat \nabla$ on
$\widehat \nabla$ on ![]() $\widehat E_G$ in some local
$\widehat E_G$ in some local ![]() $\mathcal {O}_S$-basis of
$\mathcal {O}_S$-basis of ![]() $G$ writes
$G$ writes ![]() $\mathrm {d}_{X\times S/S}\otimes \operatorname {Id}+\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i\otimes \operatorname {Id}$. Let us denote by
$\mathrm {d}_{X\times S/S}\otimes \operatorname {Id}+\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i\otimes \operatorname {Id}$. Let us denote by ![]() $\mathcal {N} x^{-\alpha }$ the
$\mathcal {N} x^{-\alpha }$ the ![]() $\mathcal {O}_{X\times S}$-module
$\mathcal {O}_{X\times S}$-module ![]() $\mathcal {N}(*D)$ for which we add to the connection the relative
$\mathcal {N}(*D)$ for which we add to the connection the relative ![]() $1$-form
$1$-form ![]() $-\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i\otimes \operatorname {Id}$. Then
$-\sum _{i=1}^\ell \alpha _i(s)\mathrm {d} x_i/x_i\otimes \operatorname {Id}$. Then ![]() $\mathcal {N} x^{-\alpha }$ is also regular holonomic, according to Corollary 4.35. As
$\mathcal {N} x^{-\alpha }$ is also regular holonomic, according to Corollary 4.35. As ![]() $\mathcal {M}=\mathcal {M}(*D)$ and
$\mathcal {M}=\mathcal {M}(*D)$ and ![]() $\mathcal {N}=\mathcal {N}(*D)$, they also are
$\mathcal {N}=\mathcal {N}(*D)$, they also are ![]() $\mathcal {D}_{X\times S/S}(*D)$-modules and, as recalled before Corollary 4.35, the functor
$\mathcal {D}_{X\times S/S}(*D)$-modules and, as recalled before Corollary 4.35, the functor ![]() $(\bullet)x^\alpha$ is an auto-equivalence of
$(\bullet)x^\alpha$ is an auto-equivalence of ![]() $\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*D))$. Therefore, we have
$\mathrm {Mod}(\mathcal {D}_{X\times S/S}(*D))$. Therefore, we have
 \begin{align*} R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M},\mathcal{N})&=R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}(*D)}(\mathcal{M},\mathcal{N})\\ &\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}(*D)}(\mathcal{M} x^{-\alpha},\mathcal{N} x^{-\alpha})\\ &=R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M} x^{-\alpha},\mathcal{N} x^{-\alpha}). \end{align*}
\begin{align*} R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M},\mathcal{N})&=R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}(*D)}(\mathcal{M},\mathcal{N})\\ &\simeq R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}(*D)}(\mathcal{M} x^{-\alpha},\mathcal{N} x^{-\alpha})\\ &=R\mathcal{H}\!\mathit{om}_{\mathcal{D}_{X\times S/S}}(\mathcal{M} x^{-\alpha},\mathcal{N} x^{-\alpha}). \end{align*}
Furthermore, ![]() $\mathcal {M} x^{-\alpha }\simeq (\mathcal {O}_{X\times S}(*D),\mathrm {d}_{X\times S/S})$. As
$\mathcal {M} x^{-\alpha }\simeq (\mathcal {O}_{X\times S}(*D),\mathrm {d}_{X\times S/S})$. As ![]() $\operatorname {DR}(\mathcal {N} x^{-\alpha })$ is
$\operatorname {DR}(\mathcal {N} x^{-\alpha })$ is ![]() $S$-
$S$-![]() $\mathbb {C}$-constructible (cf. [Reference Monteiro Fernandes and SabbahMFS13, Theorem 3.7]) and
$\mathbb {C}$-constructible (cf. [Reference Monteiro Fernandes and SabbahMFS13, Theorem 3.7]) and ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}([\mathcal {O}_{X\times S}(*D)/\mathcal {O}_{X\times S}],\mathcal {N} x^{-\alpha })$ also by
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}([\mathcal {O}_{X\times S}(*D)/\mathcal {O}_{X\times S}],\mathcal {N} x^{-\alpha })$ also by ![]() $\textrm{ (6.6)}_{d,k-1}$, we conclude that
$\textrm{ (6.6)}_{d,k-1}$, we conclude that ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M},\mathcal {N})$ belongs to
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M},\mathcal {N})$ belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$.
Lemma 6.16 Let us assume that ![]() $\textrm{ (6.6)}_{d,k,r-1}$ holds (
$\textrm{ (6.6)}_{d,k,r-1}$ holds (![]() $r\geqslant 2$). Then
$r\geqslant 2$). Then ![]() $\textrm{ (6.6)}_{d,k,r}$ holds.
$\textrm{ (6.6)}_{d,k,r}$ holds.
Proof. Let us assume that ![]() $r\geqslant 2$. Together with the assumptions of (6.13) in step 4, we can now assume that
$r\geqslant 2$. Together with the assumptions of (6.13) in step 4, we can now assume that ![]() $G$ is
$G$ is ![]() $\mathcal {O}_S$-locally free of finite rank
$\mathcal {O}_S$-locally free of finite rank ![]() $r$ (Lemma 6.14) and thus, by Proposition 4.25(i),
$r$ (Lemma 6.14) and thus, by Proposition 4.25(i), ![]() $\mathcal {M}\simeq (\widehat E_G,\widehat \nabla )$. We argue in a way similar to that in step 4 in the proof of Theorem 4.15(iii).
$\mathcal {M}\simeq (\widehat E_G,\widehat \nabla )$. We argue in a way similar to that in step 4 in the proof of Theorem 4.15(iii).
If each endomorphism ![]() $A_i(s)$ occurring in the connection matrix of
$A_i(s)$ occurring in the connection matrix of ![]() $\nabla$ is scalar, i.e., of the form
$\nabla$ is scalar, i.e., of the form ![]() $\alpha _i(s)\operatorname {Id}$, then Lemma 6.15 allows us to conclude, by obvious reduction to rank one, the proof of
$\alpha _i(s)\operatorname {Id}$, then Lemma 6.15 allows us to conclude, by obvious reduction to rank one, the proof of ![]() $\textrm{ (6.6)}$ for
$\textrm{ (6.6)}$ for ![]() $\mathcal {M}=(\widehat E_G,\widehat \nabla )$ and
$\mathcal {M}=(\widehat E_G,\widehat \nabla )$ and ![]() $\mathcal {N}$ as previously.
$\mathcal {N}$ as previously.
We can thus assume that some endomorphism ![]() $A_i(s)$, say
$A_i(s)$, say ![]() $A_1(s)$, is not scalar. We use the notation of step 4 in the proof of Theorem 4.15(iii), in particular (4.21) and (4.22). Recall that we consider the composition
$A_1(s)$, is not scalar. We use the notation of step 4 in the proof of Theorem 4.15(iii), in particular (4.21) and (4.22). Recall that we consider the composition ![]() $S'\stackrel {\pi }{\longrightarrow }\Sigma \stackrel {\sigma }{\longrightarrow } S$, with
$S'\stackrel {\pi }{\longrightarrow }\Sigma \stackrel {\sigma }{\longrightarrow } S$, with ![]() $\Sigma :=\{\det (\alpha _1\operatorname {Id}-A_1(s))=0\}$ and
$\Sigma :=\{\det (\alpha _1\operatorname {Id}-A_1(s))=0\}$ and ![]() $\pi :S'\rightarrow \Sigma$ is a resolution of singularities.
$\pi :S'\rightarrow \Sigma$ is a resolution of singularities.
Recall also that we set ![]() $G'=\ker (\alpha _1\operatorname {Id}-\mathsf {A}_1\circ \sigma \circ \pi )\subset (\sigma \circ \pi )^*G$ and we consider the exact sequence
$G'=\ker (\alpha _1\operatorname {Id}-\mathsf {A}_1\circ \sigma \circ \pi )\subset (\sigma \circ \pi )^*G$ and we consider the exact sequence ![]() $0\rightarrow G'\rightarrow (\sigma \circ \pi )^*G\rightarrow G''\to 0$. By construction and assumption, we have
$0\rightarrow G'\rightarrow (\sigma \circ \pi )^*G\rightarrow G''\to 0$. By construction and assumption, we have ![]() $1\leqslant \operatorname {rk} G'<\operatorname {rk} G$ and thus
$1\leqslant \operatorname {rk} G'<\operatorname {rk} G$ and thus ![]() $\operatorname {rk} G''<\operatorname {rk} G$.
$\operatorname {rk} G''<\operatorname {rk} G$.
By applying the induction hypothesis ![]() $\textrm{ (6.6)}_{d,k,r-1}$ to
$\textrm{ (6.6)}_{d,k,r-1}$ to ![]() $G',G''$, we deduce that
$G',G''$, we deduce that
belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, hence so does its pushforward by
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, hence so does its pushforward by ![]() $\sigma \circ \pi$. Thus,
$\sigma \circ \pi$. Thus,
belongs to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ by Lemma 2.16.
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$ by Lemma 2.16.
The cones of the natural morphisms
and
are supported on ![]() $X\times \sigma (\mathrm {Sing}(\Sigma ))$. Therefore,
$X\times \sigma (\mathrm {Sing}(\Sigma ))$. Therefore,
Recalling (cf. (4.21)) that locally ![]() $\sigma _*\mathcal {O}_{X\times \Sigma }$ is
$\sigma _*\mathcal {O}_{X\times \Sigma }$ is ![]() $\mathcal {O}_{X\times S}$-free of rank
$\mathcal {O}_{X\times S}$-free of rank ![]() $\deg \sigma$,
$\deg \sigma$, ![]() $\sigma _*\sigma ^*\mathcal {N}$, which is isomorphic to
$\sigma _*\sigma ^*\mathcal {N}$, which is isomorphic to ![]() $\sigma _*\mathcal {O}_{X\times \Sigma }\otimes _{\mathcal {O}_{X\times S}}\mathcal {N}$, is regular holonomic. In addition, according to (4.22),
$\sigma _*\mathcal {O}_{X\times \Sigma }\otimes _{\mathcal {O}_{X\times S}}\mathcal {N}$, is regular holonomic. In addition, according to (4.22), ![]() $\mathcal {N}$ is a direct summand of
$\mathcal {N}$ is a direct summand of ![]() $\sigma _*\sigma ^*\mathcal {N}$. Therefore,
$\sigma _*\sigma ^*\mathcal {N}$. Therefore, ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$ is a direct summand of
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$ is a direct summand of ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \sigma _*\sigma ^*\mathcal {N})$, thus again by
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \sigma _*\sigma ^*\mathcal {N})$, thus again by ![]() $\textrm{ (6.6)}_{d-1}$,
$\textrm{ (6.6)}_{d-1}$, ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \sigma _*\sigma ^*\mathcal {N})$ is an object of
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \sigma _*\sigma ^*\mathcal {N})$ is an object of ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, hence the same holds true for
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {C} {-c}}}(p^{-1}\mathcal {O}_S)$, hence the same holds true for ![]() $R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$.
$R\mathcal {H}\!\mathit {om}_{\mathcal {D}_{X\times S/S}}(\mathcal {M}, \mathcal {N})$.
This lemma concludes step 5, therefore the proof of ![]() $\textrm{ (6.6)}_d$, and thereby that of Theorem 2.
$\textrm{ (6.6)}_d$, and thereby that of Theorem 2.
As a consequence of Theorem 2 we can now generalize Proposition 4.26.
Theorem 6.17 Let ![]() $Y$ be a hypersurface in
$Y$ be a hypersurface in ![]() $X$. Then the category of
$X$. Then the category of ![]() $\mathcal {D}_{X\times S/S}$-modules of D-type along
$\mathcal {D}_{X\times S/S}$-modules of D-type along ![]() $Y$ is equivalent to the category of
$Y$ is equivalent to the category of ![]() $S$-locally constant sheaves on
$S$-locally constant sheaves on ![]() $X^*\times S$ with finite rank, under the functor
$X^*\times S$ with finite rank, under the functor ![]() $\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ with quasi-inverse
$\mathcal {L}\mapsto L=\mathcal {H}^0\operatorname {DR}(\mathcal {L}_{|X^*\times S})$ with quasi-inverse ![]() $L\rightarrow \operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$.
$L\rightarrow \operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$.
Proof. Let us prove that the second functor takes values in the category of modules of ![]() $D$-type along
$D$-type along ![]() $Y$. Let
$Y$. Let ![]() $L$ be an
$L$ be an ![]() $S$-locally constant sheaf on
$S$-locally constant sheaf on ![]() $X^*\times S$ of finite rank. As, by [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 2.6] (valid without any restriction on
$X^*\times S$ of finite rank. As, by [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 2.6] (valid without any restriction on ![]() $\dim S$),
$\dim S$), ![]() $\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)$ is localized along
$\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)$ is localized along ![]() $Y$, and regular holonomic by Theorem 2, hence
$Y$, and regular holonomic by Theorem 2, hence ![]() $\mathcal {D}_{X\times S/S}(*Y)$-coherent, it remains to prove that
$\mathcal {D}_{X\times S/S}(*Y)$-coherent, it remains to prove that ![]() $\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$ is in degree zero and that
$\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$ is in degree zero and that ![]() $\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]|_{X^*\times S}\simeq \mathcal {O}_{X^*\times S}\otimes _{p_{X^*}^{-1}\mathcal {O}_S}L$. The first assertion follows by the usual Nakayama-type argument. The second assertion follows from [Reference Monteiro Fernandes and SabbahMFS19, Corollary 3.24] (valid without any restriction on
$\operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]|_{X^*\times S}\simeq \mathcal {O}_{X^*\times S}\otimes _{p_{X^*}^{-1}\mathcal {O}_S}L$. The first assertion follows by the usual Nakayama-type argument. The second assertion follows from [Reference Monteiro Fernandes and SabbahMFS19, Corollary 3.24] (valid without any restriction on ![]() $\dim S$), which shows that
$\dim S$), which shows that ![]() $\operatorname {RH}_{X^*}^S(\boldsymbol {D}'L)[-d_X]\simeq \mathcal {O}_{X^*\times S}\otimes _{p^{-1}_{X^*}\mathcal {O}_S}L$.
$\operatorname {RH}_{X^*}^S(\boldsymbol {D}'L)[-d_X]\simeq \mathcal {O}_{X^*\times S}\otimes _{p^{-1}_{X^*}\mathcal {O}_S}L$.
Let ![]() $\mathcal {L}$ be a
$\mathcal {L}$ be a ![]() $\mathcal {D}_{X\times S/S}$-module of
$\mathcal {D}_{X\times S/S}$-module of ![]() $D$-type along
$D$-type along ![]() $Y$ with the associated
$Y$ with the associated ![]() $S$-local system
$S$-local system ![]() $L$, that is
$L$, that is ![]() $\operatorname {DR}(\mathcal {L})|_{X^*\times S}\simeq L$; we have a natural morphism
$\operatorname {DR}(\mathcal {L})|_{X^*\times S}\simeq L$; we have a natural morphism ![]() $\operatorname {DR}(\mathcal {L})\rightarrow j_*L$. By Corollary 4.33,
$\operatorname {DR}(\mathcal {L})\rightarrow j_*L$. By Corollary 4.33, ![]() $\mathcal {L}$ is regular holonomic. According to Lemma 5.16,
$\mathcal {L}$ is regular holonomic. According to Lemma 5.16, ![]() $\operatorname {DR}(\operatorname {RH}^S_X(j_!\boldsymbol {D}'L)[-d_X])\simeq j_*L$, thus, by Theorem 2, there exists a natural morphism of localized regular holonomic
$\operatorname {DR}(\operatorname {RH}^S_X(j_!\boldsymbol {D}'L)[-d_X])\simeq j_*L$, thus, by Theorem 2, there exists a natural morphism of localized regular holonomic ![]() $\mathcal {D}_{X\times S/S}$-modules
$\mathcal {D}_{X\times S/S}$-modules ![]() $\mathcal {L}\rightarrow \operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$, which has to be an isomorphism because that is the case on
$\mathcal {L}\rightarrow \operatorname {RH}_X^S(j_!\boldsymbol {D}'L)[-d_X]$, which has to be an isomorphism because that is the case on ![]() $X^*\times S$.
$X^*\times S$.
Acknowledgements
We thank L. Prelli and P. Schapira for useful discussions and suggestions. We thank H. Esnault for pointing out to us the preprint [Reference Hai, dos Santos and TâmHdST21], and its authors for interesting discussions. We are deeply grateful to the referee whose comments helped us to rethink and thus to improve our work.
The research of L. Fiorot was supported by project PRIN 2017 Categories, Algebras: Ring-Theoretical and Homological Approaches (CARTHA). The research of T. Monteiro Fernandes was supported by Fundação para a Ciência e Tecnologia, under the project: UIDB/04561/2020.
Conflicts of Interest
None.
Appendix: Complements
The aim of this appendix is twofold:
• to prove Proposition 5.4, thus correcting the statement of [Reference Monteiro Fernandes and SabbahMFS19, Proposition 3.5] (namely, in contrast to [Reference Monteiro Fernandes and SabbahMFS19, Proposition 3.5], the resolution in Proposition 5.4 may be not bounded below); and
• to correct and complete the contents of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, §1.2.2].
Taking into account these corrections, the main results in both articles remain valid.
Furthermore, for the sake of completeness, we give a detailed proof of Lemma 5.14, by following the same strategy as in [Reference Kashiwara and SchapiraKS96, Theorem 4.4].
In the following, we use the notation ![]() $\mathcal {O}_V$ for
$\mathcal {O}_V$ for ![]() $\mathbb {C}_V\otimes \mathcal {O}_S$, for any open set
$\mathbb {C}_V\otimes \mathcal {O}_S$, for any open set ![]() $V\subset S$. Recall that, for
$V\subset S$. Recall that, for ![]() $\Omega, \Omega '$ open in
$\Omega, \Omega '$ open in ![]() $X$ and
$X$ and ![]() $V$,
$V$, ![]() $V'$ open in
$V'$ open in ![]() $S$, for any
$S$, for any ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $G$, we have:
$G$, we have:
•
 $\operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(\mathbb {C}_{\Omega }\boxtimes \mathcal {O}_V, \mathbb {C}_{\Omega '\times V'}\otimes p_X^{-1}G) \simeq \Gamma (\Omega \times V; p_X^{-1}G)$ if
$\operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(\mathbb {C}_{\Omega }\boxtimes \mathcal {O}_V, \mathbb {C}_{\Omega '\times V'}\otimes p_X^{-1}G) \simeq \Gamma (\Omega \times V; p_X^{-1}G)$ if  $\Omega \subset \Omega '$ and
$\Omega \subset \Omega '$ and  $V\subset V'$;
$V\subset V'$;• if
 $\Omega \times V\cap \overline {\Omega '\times V'}=\varnothing$, then
$\Omega \times V\cap \overline {\Omega '\times V'}=\varnothing$, then  $\operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(\mathbb {C}_{\Omega }\boxtimes \mathcal {O}_V, \mathbb {C}_{\Omega '\times V'}\otimes p_X^{-1}G)=0$.
$\operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(\mathbb {C}_{\Omega }\boxtimes \mathcal {O}_V, \mathbb {C}_{\Omega '\times V'}\otimes p_X^{-1}G)=0$.
We consider the family ![]() $\mathcal {S}=\mathcal {S}_X\times \mathcal {S}_S$ of open sets
$\mathcal {S}=\mathcal {S}_X\times \mathcal {S}_S$ of open sets ![]() $W=U\times V$ of
$W=U\times V$ of ![]() $X\times S$, where:
$X\times S$, where:
(i)
 $U$ is connected open subanalytic relatively compact in
$U$ is connected open subanalytic relatively compact in  $X$;
$X$;(ii)
 $V$ is open and relatively compact in
$V$ is open and relatively compact in  $S$.
$S$.
This family satisfies the conditions of [Reference Kashiwara and SchapiraKS96, (A.7) and (A.8)], because each point of ![]() $X\times S$ has a fundamental system of neighborhoods consisting of open sets in
$X\times S$ has a fundamental system of neighborhoods consisting of open sets in ![]() $\mathcal {S}$, and the intersection of two open sets of
$\mathcal {S}$, and the intersection of two open sets of ![]() $\mathcal {S}$ is a finite union of elements in
$\mathcal {S}$ is a finite union of elements in ![]() $\mathcal {S}$.
$\mathcal {S}$.
Note that for any ![]() $W_1=U_1\times V_1, W_2=U_2\times V_2\in \mathcal {S}$ we have
$W_1=U_1\times V_1, W_2=U_2\times V_2\in \mathcal {S}$ we have
 \begin{equation} \Gamma(W_1;\mathbb{C}_{W_2}\otimes p_X^{-1}\mathcal{O}_S)= \begin{cases} \Gamma(W_1; p_X^{-1}\mathcal{O}_{V_2})=\Gamma(V_1; \mathcal{O}_{V_2}) & \text{if }U_1\subset U_2,\\ 0 & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} \Gamma(W_1;\mathbb{C}_{W_2}\otimes p_X^{-1}\mathcal{O}_S)= \begin{cases} \Gamma(W_1; p_X^{-1}\mathcal{O}_{V_2})=\Gamma(V_1; \mathcal{O}_{V_2}) & \text{if }U_1\subset U_2,\\ 0 & \text{otherwise}. \end{cases} \end{equation}Definition A.2 In a similar way to [Reference Kashiwara and SchapiraKS96, § A.2], we define:
•
 ${\mathbf {A}}_X=\mathrm {Mod}_{ {w-}\mathbb {R} {-c}}(p_X^{-1}\mathcal {O}_S)$;
${\mathbf {A}}_X=\mathrm {Mod}_{ {w-}\mathbb {R} {-c}}(p_X^{-1}\mathcal {O}_S)$;•
 ${\mathbf {P}}_X$ the category whose objects
${\mathbf {P}}_X$ the category whose objects  $\mathfrak {W}=(W_i=U_i\times V_i)_{i\in I}$ consist of locally finite families of open subsets of
$\mathfrak {W}=(W_i=U_i\times V_i)_{i\in I}$ consist of locally finite families of open subsets of  $\mathcal {S}$, and whose morphisms are described in a way similar to that of [Reference Kashiwara and SchapiraKS96, § A.2],
where
$\mathcal {S}$, and whose morphisms are described in a way similar to that of [Reference Kashiwara and SchapiraKS96, § A.2],
where \[ \operatorname{Hom}_{{\mathbf{P}}_X}(\mathfrak{W},\mathfrak{W}')=\mathop{\textstyle\prod}\limits_{i\in I}\bigg(\mathop{\textstyle\bigoplus}\limits_{j\in J\mid W'_j\supset W_i}\Gamma(U_i\times\overline{V_i};p_X^{-1}\mathcal{O}_S)\bigg), \]
\[ \operatorname{Hom}_{{\mathbf{P}}_X}(\mathfrak{W},\mathfrak{W}')=\mathop{\textstyle\prod}\limits_{i\in I}\bigg(\mathop{\textstyle\bigoplus}\limits_{j\in J\mid W'_j\supset W_i}\Gamma(U_i\times\overline{V_i};p_X^{-1}\mathcal{O}_S)\bigg), \]
 $\mathfrak {W}'=(W'_j=U'_j\times V'_j)_{j\in J}$;
$\mathfrak {W}'=(W'_j=U'_j\times V'_j)_{j\in J}$;• in the following we write simply
 ${\mathbf {A}}, {\mathbf {P}}$ in order to keep the notation clean; the additive functor
${\mathbf {A}}, {\mathbf {P}}$ in order to keep the notation clean; the additive functor  $L:{\mathbf {P}} \rightarrow {\mathbf {A}}$ given by
and, for
$L:{\mathbf {P}} \rightarrow {\mathbf {A}}$ given by
and, for \[ L(\mathfrak{W})=\mathop{\textstyle\bigoplus}\limits_{i\in I} \mathbb{C}_{U_i}\boxtimes {\mathcal{O}}_{V_i}=\mathop{\textstyle\bigoplus}\limits_{i\in I}(\mathbb{C}_{W_i}\otimes p_X^{-1}\mathcal{O}_S), \]
\[ L(\mathfrak{W})=\mathop{\textstyle\bigoplus}\limits_{i\in I} \mathbb{C}_{U_i}\boxtimes {\mathcal{O}}_{V_i}=\mathop{\textstyle\bigoplus}\limits_{i\in I}(\mathbb{C}_{W_i}\otimes p_X^{-1}\mathcal{O}_S), \]
 $\mathfrak {W},\, \mathfrak {W}'\in {\mathbf {P}}$, for
$\mathfrak {W},\, \mathfrak {W}'\in {\mathbf {P}}$, for  $\varphi \in \operatorname {Hom}_{{\mathbf {P}}}(\mathfrak {W}, \mathfrak {W}')$,
$\varphi \in \operatorname {Hom}_{{\mathbf {P}}}(\mathfrak {W}, \mathfrak {W}')$,  $L(\varphi )$ is given by the natural morphism
for each
$L(\varphi )$ is given by the natural morphism
for each \[ \Gamma(U_i\times \overline{V_i}; p_X^{-1}\mathcal{O}_S)\longrightarrow \Gamma(U_i\times V_i; \mathbb{C}_{U_j}\boxtimes \mathcal{O}_{V_j})=\Gamma(W_i; p_X^{-1}\mathcal{O}_S) \]
\[ \Gamma(U_i\times \overline{V_i}; p_X^{-1}\mathcal{O}_S)\longrightarrow \Gamma(U_i\times V_i; \mathbb{C}_{U_j}\boxtimes \mathcal{O}_{V_j})=\Gamma(W_i; p_X^{-1}\mathcal{O}_S) \]
 $i\in I,\, j\in J$ such that
$i\in I,\, j\in J$ such that  $W_i\subset W_j$; we remark that
$W_i\subset W_j$; we remark that  $L$ is a faithful functor;
$L$ is a faithful functor;• the additive bi-functor
 $H:{\mathbf {P}}^{\mathrm {op}}\times {\mathbf {A}}\rightarrow {\mathbf {Ab}}$ given, for
$H:{\mathbf {P}}^{\mathrm {op}}\times {\mathbf {A}}\rightarrow {\mathbf {Ab}}$ given, for  $\mathfrak {W}\in {\mathbf {P}}$ and
$\mathfrak {W}\in {\mathbf {P}}$ and  $F\in {\mathbf {A}}$, by
where, following the notation of [Reference Kashiwara and SchapiraKS96, Appendix A.1],
$F\in {\mathbf {A}}$, by
where, following the notation of [Reference Kashiwara and SchapiraKS96, Appendix A.1], \[ H(\mathfrak{W}, F)=\mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times \overline{V_i}; F), \]
\[ H(\mathfrak{W}, F)=\mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times \overline{V_i}; F), \]
 ${\mathbf {Ab}}$ denotes the category of abelian groups;
${\mathbf {Ab}}$ denotes the category of abelian groups;•
 $\alpha _{\mathfrak {W}, F}: H(\mathfrak {W}, F)\rightarrow \operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(L(\mathfrak {W}), F)$ given by the restrictions
$\alpha _{\mathfrak {W}, F}: H(\mathfrak {W}, F)\rightarrow \operatorname {Hom}_{p_X^{-1}\mathcal {O}_S}(L(\mathfrak {W}), F)$ given by the restrictions
 \[ \mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times \overline{V_i}; F) \longrightarrow\mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times V_i; F)= \operatorname{Hom}_{p_X^{-1}\mathcal{O}_S}\bigg(\mathop{\textstyle\bigoplus}\limits_{i\in I} \mathbb{C}_{U_i}\boxtimes {\mathcal{O}}_{V_i}; F\bigg). \]
\[ \mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times \overline{V_i}; F) \longrightarrow\mathop{\textstyle\prod}\limits_{i\in I}\Gamma(U_i\times V_i; F)= \operatorname{Hom}_{p_X^{-1}\mathcal{O}_S}\bigg(\mathop{\textstyle\bigoplus}\limits_{i\in I} \mathbb{C}_{U_i}\boxtimes {\mathcal{O}}_{V_i}; F\bigg). \]
For a morphism ![]() $u$ in
$u$ in ![]() ${\mathbf {P}}$ let us denote by
${\mathbf {P}}$ let us denote by ![]() $\ker u$ (respectively,
$\ker u$ (respectively, ![]() $\operatorname {im} u$) the kernel (respectively, the image) of
$\operatorname {im} u$) the kernel (respectively, the image) of ![]() $L(u)$ as a morphism in
$L(u)$ as a morphism in ![]() ${\mathbf {A}}$.
${\mathbf {A}}$.
An object ![]() $F$ of
$F$ of ![]() ${\mathbf {A}}$ is called
${\mathbf {A}}$ is called ![]() ${\mathbf {P}}$-coherent [Reference Kashiwara and SchapiraKS96, Appendix A.1] if there exist
${\mathbf {P}}$-coherent [Reference Kashiwara and SchapiraKS96, Appendix A.1] if there exist ![]() $\mathfrak {W}\in {\mathbf {P}}$ and an epimorphism
$\mathfrak {W}\in {\mathbf {P}}$ and an epimorphism ![]() $L(\mathfrak {W})\rightarrow F$ in
$L(\mathfrak {W})\rightarrow F$ in ![]() ${\mathbf {A}}$ and if, for any
${\mathbf {A}}$ and if, for any ![]() $f\in H(\mathfrak {W}', F)$, there exist
$f\in H(\mathfrak {W}', F)$, there exist ![]() $\mathfrak {W}''$ in
$\mathfrak {W}''$ in ![]() ${\mathbf {P}}$ and a morphism
${\mathbf {P}}$ and a morphism ![]() $g:\mathfrak {W}''\rightarrow \mathfrak {W}'$ such that
$g:\mathfrak {W}''\rightarrow \mathfrak {W}'$ such that ![]() $\mathfrak {W}''\overset {g}\rightarrow \mathfrak {W}'\overset {f}\rightarrow F$ is exact; that is
$\mathfrak {W}''\overset {g}\rightarrow \mathfrak {W}'\overset {f}\rightarrow F$ is exact; that is ![]() $L(\mathfrak {W}'')\overset {L(g)}{\rightarrow }L(\mathfrak {W}')\overset {\alpha (f)}{\rightarrow } F$ is exact in
$L(\mathfrak {W}'')\overset {L(g)}{\rightarrow }L(\mathfrak {W}')\overset {\alpha (f)}{\rightarrow } F$ is exact in ![]() ${\mathbf {A}}$ (and, hence,
${\mathbf {A}}$ (and, hence, ![]() $f\circ g = 0$ because
$f\circ g = 0$ because ![]() $L$ is faithful).
$L$ is faithful).
Proposition A.3
(i) The objects
 $({\mathbf {A}},{\mathbf {P}},L,H,\alpha )$ as defined previously satisfy Properties (A.1)–(A.4) of [Reference Kashiwara and SchapiraKS96, § A.1].
$({\mathbf {A}},{\mathbf {P}},L,H,\alpha )$ as defined previously satisfy Properties (A.1)–(A.4) of [Reference Kashiwara and SchapiraKS96, § A.1].(ii) An object of
 ${\mathbf {A}}$ is
${\mathbf {A}}$ is  ${\mathbf {P}}$-coherent if and only if it is
${\mathbf {P}}$-coherent if and only if it is  $S$-
$S$- $\mathbb {R}$-constructible.
$\mathbb {R}$-constructible.
The proof of Proposition A.3(i), which concerns the ring ![]() $p_X^{-1}\mathcal {O}_S$, essentially reduces that of [Reference Kashiwara and SchapiraKS96, Proposition A.6], which concerns the ring
$p_X^{-1}\mathcal {O}_S$, essentially reduces that of [Reference Kashiwara and SchapiraKS96, Proposition A.6], which concerns the ring ![]() $\mathcal {O}_S$. However, the new ingredient with respect to [Reference Kashiwara and SchapiraKS96] is the property that any
$\mathcal {O}_S$. However, the new ingredient with respect to [Reference Kashiwara and SchapiraKS96] is the property that any ![]() $S$-weakly
$S$-weakly ![]() $\mathbb {R}$-constructible sheaf
$\mathbb {R}$-constructible sheaf ![]() $F$ admits an epimorphism
$F$ admits an epimorphism ![]() $u:\mathop {\textstyle \bigoplus } _k(\mathbb {C}_{U_k}\boxtimes G_k)\rightarrow F$ for some locally finite family
$u:\mathop {\textstyle \bigoplus } _k(\mathbb {C}_{U_k}\boxtimes G_k)\rightarrow F$ for some locally finite family ![]() $(U_k)$ in
$(U_k)$ in ![]() $\mathcal {S}_X$ and some
$\mathcal {S}_X$ and some ![]() $\mathcal {O}_S$-modules
$\mathcal {O}_S$-modules ![]() $G_k$, which can be assumed to be
$G_k$, which can be assumed to be ![]() $\mathcal {O}_S$-coherent if
$\mathcal {O}_S$-coherent if ![]() $F$ is
$F$ is ![]() $S$-
$S$-![]() $\mathbb {R}$-constructible. Details are given in the arXiv version of this paper.
$\mathbb {R}$-constructible. Details are given in the arXiv version of this paper.
Corollary A.4 The category of ![]() ${\mathbf {P}}$-coherent objects is closed under kernels, cokernels, and extensions in
${\mathbf {P}}$-coherent objects is closed under kernels, cokernels, and extensions in ![]() ${\mathbf {A}}$.
${\mathbf {A}}$.
Proof. This is [Reference Kashiwara and SchapiraKS96, Proposition A.1], that we can apply according to Proposition A.3.
As in [Reference Kashiwara and SchapiraKS96, Appendix], we denote by ![]() $\operatorname {\mathsf {D}}^-({\mathbf {P}})$ (respectively,
$\operatorname {\mathsf {D}}^-({\mathbf {P}})$ (respectively, ![]() $\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$) the triangulated category obtained by taking the quotient of
$\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$) the triangulated category obtained by taking the quotient of ![]() $\operatorname {\mathsf {K}}^-({\mathbf {P}})$ (respectively,
$\operatorname {\mathsf {K}}^-({\mathbf {P}})$ (respectively, ![]() $\operatorname {\mathsf {K}}^\mathrm {b}({\mathbf {P}})$) with respect to the null system of complexes
$\operatorname {\mathsf {K}}^\mathrm {b}({\mathbf {P}})$) with respect to the null system of complexes ![]() $\mathfrak {W}^{\bullet}$ in
$\mathfrak {W}^{\bullet}$ in ![]() ${\mathbf {P}}$ such that
${\mathbf {P}}$ such that ![]() $L(\mathfrak {W}^{\bullet})$ is acyclic in
$L(\mathfrak {W}^{\bullet})$ is acyclic in ![]() ${\mathbf {A}}$. We denote by
${\mathbf {A}}$. We denote by ![]() $\operatorname {\mathsf {D}}^-_\mathrm {coh}({\mathbf {P}})$ the full subcategory of
$\operatorname {\mathsf {D}}^-_\mathrm {coh}({\mathbf {P}})$ the full subcategory of ![]() $\operatorname {\mathsf {D}}^-({\mathbf {P}})$ of objects
$\operatorname {\mathsf {D}}^-({\mathbf {P}})$ of objects ![]() $\mathfrak {W}^{\bullet}$ such that
$\mathfrak {W}^{\bullet}$ such that ![]() $L(\mathfrak {W}^{\bullet})$ has
$L(\mathfrak {W}^{\bullet})$ has ![]() ${\mathbf {P}}$-coherent cohomologies.
${\mathbf {P}}$-coherent cohomologies.
On the other hand, we denote by ![]() $\operatorname {\mathsf {D}}^-_\mathrm {coh}({\mathbf {A}})$ (respectively,
$\operatorname {\mathsf {D}}^-_\mathrm {coh}({\mathbf {A}})$ (respectively, ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$) the full subcategory of
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$) the full subcategory of ![]() $\operatorname {\mathsf {D}}^-({\mathbf {A}})$ (respectively,
$\operatorname {\mathsf {D}}^-({\mathbf {A}})$ (respectively, ![]() $\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {A}})$) whose objects have
$\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {A}})$) whose objects have ![]() ${\mathbf {P}}$-coherent cohomologies, i.e., according to Proposition A.3(ii), are
${\mathbf {P}}$-coherent cohomologies, i.e., according to Proposition A.3(ii), are ![]() $S$-
$S$-![]() $\mathbb {R}$-constructible. We also denote by
$\mathbb {R}$-constructible. We also denote by ![]() $\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ the full subcategory of
$\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ the full subcategory of ![]() $\operatorname {\mathsf {D}}^-({\mathbf {P}})$ of objects
$\operatorname {\mathsf {D}}^-({\mathbf {P}})$ of objects ![]() $\mathfrak {W}^{\bullet}$ such that
$\mathfrak {W}^{\bullet}$ such that ![]() $L(\mathfrak {W}^{\bullet})\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$.
$L(\mathfrak {W}^{\bullet})\in \operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$.
In this context, [Reference Kashiwara and SchapiraKS90, Proposition 8.1.4] holds with a similar proof and provides functorial isomorphisms, for any ![]() $F$ in
$F$ in ![]() ${\mathbf {A}}$, any
${\mathbf {A}}$, any ![]() $\sigma \in \Delta$ and any
$\sigma \in \Delta$ and any ![]() $x\in |\sigma |$:
$x\in |\sigma |$:
The proofs of [Reference Kashiwara and SchapiraKS90, Theorem 8.1.10 and 8.4.5(i)] can then be adapted to the relative setting by replacing everywhere the functor ![]() $\Gamma (U(\sigma ),\bullet)$ with
$\Gamma (U(\sigma ),\bullet)$ with ![]() $p_{U(\sigma )*}(\bullet|_{U(\sigma )})$, yielding that the natural inclusion functor
$p_{U(\sigma )*}(\bullet|_{U(\sigma )})$, yielding that the natural inclusion functor ![]() $\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {A}})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{ {w-}\mathbb {R} {-c}}(p_X^{-1}\mathcal {O}_S)$ is an equivalence by providing an explicit quasi-inverse denoted there by
$\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {A}})\rightarrow \operatorname {\mathsf {D}}^\mathrm {b}_{ {w-}\mathbb {R} {-c}}(p_X^{-1}\mathcal {O}_S)$ is an equivalence by providing an explicit quasi-inverse denoted there by ![]() $R\beta$. We deduce an equivalence
$R\beta$. We deduce an equivalence
The following proposition, which is a consequence of [Reference Kashiwara and SchapiraKS96, Theorem A.5] and the properties explained previously, corrects [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 1.6].
Proposition A.6 The natural functor
is an equivalence of categories which induces an equivalence of categories (still denoted by ![]() $L$ for brevity)
$L$ for brevity)
Proof of Proposition 5.4 We identify ![]() $\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ with its essential image in
$\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ with its essential image in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$, which is thus equivalent to
$\operatorname {\mathsf {D}}^\mathrm {b}_\mathrm {coh}({\mathbf {A}})$, which is thus equivalent to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, according to Proposition A.6. By definition, the objects
$\operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, according to Proposition A.6. By definition, the objects ![]() $K^\bullet$ in this essential image satisfy the property described in Proposition 5.4.
$K^\bullet$ in this essential image satisfy the property described in Proposition 5.4.
Remark A.7 In (5.13) we defined the natural transformation ![]() $\mu :{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(\bullet)\rightarrow \operatorname {TH}_Y^S(Rf_*(\bullet))$ between functors from
$\mu :{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(\bullet)\rightarrow \operatorname {TH}_Y^S(Rf_*(\bullet))$ between functors from ![]() $\operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ to
$\operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. Due to Proposition A.6 we get (by composing with
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. Due to Proposition A.6 we get (by composing with ![]() $L$) a natural transformation
$L$) a natural transformation
between functors from ![]() $\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ to
$\operatorname {\mathsf {D}}^-_{\mathrm {b}, \mathrm {coh}}({\mathbf {P}})$ to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. We now extend it, by relaxing the coherency condition, to a natural transformation between functors from
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. We now extend it, by relaxing the coherency condition, to a natural transformation between functors from ![]() $\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$ to
$\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$ to ![]() $\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. Recall that we denote by
$\operatorname {\mathsf {D}}^\mathrm {b}(\mathcal {D}_{Y\times S/S})$. Recall that we denote by ![]() $f$ both maps
$f$ both maps ![]() $X\rightarrow Y$ and
$X\rightarrow Y$ and ![]() $X\times S\to Y\times S$. Let
$X\times S\to Y\times S$. Let ![]() $W=U\times V\in \mathcal {S}$ and consider the family
$W=U\times V\in \mathcal {S}$ and consider the family ![]() $\{W\}$. By adjunction we have
$\{W\}$. By adjunction we have
and thus
As ![]() $f^{-1}Rf_*(\mathbb {C}_{U})$ is a bounded complex with
$f^{-1}Rf_*(\mathbb {C}_{U})$ is a bounded complex with ![]() $\mathbb {R}$-constructible cohomologies, it is quasi-isomorphic to a bounded complex whose entries are locally finite sums
$\mathbb {R}$-constructible cohomologies, it is quasi-isomorphic to a bounded complex whose entries are locally finite sums ![]() $\mathop {\textstyle \bigoplus } _{i\in I}\mathbb {C}_{U_i}$ where each
$\mathop {\textstyle \bigoplus } _{i\in I}\mathbb {C}_{U_i}$ where each ![]() $U_i\in \mathcal {S}_X$ (cf. [Reference D'Agnolo, Guillermou and SchapiraDGS11, Proposition A.1]). Therefore, the complex
$U_i\in \mathcal {S}_X$ (cf. [Reference D'Agnolo, Guillermou and SchapiraDGS11, Proposition A.1]). Therefore, the complex ![]() $f^{-1}Rf_*L(\{W\})$ belongs to the essential image by
$f^{-1}Rf_*L(\{W\})$ belongs to the essential image by ![]() $L$ of a complex in
$L$ of a complex in ![]() $\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$. The same property then holds for any
$\operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$. The same property then holds for any ![]() $\mathfrak {W}\in {\mathbf {P}}$ instead of
$\mathfrak {W}\in {\mathbf {P}}$ instead of ![]() $\{W\}$ and then for any bounded complex
$\{W\}$ and then for any bounded complex ![]() $\mathfrak {W}^\bullet\in \operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$.
$\mathfrak {W}^\bullet\in \operatorname {\mathsf {D}}^\mathrm {b}({\mathbf {P}})$.
It is then meaningful to define ![]() $\mu _{L(\mathfrak {W}^\bullet)}:{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(L(\mathfrak {W}^\bullet))\rightarrow \operatorname {TH}_Y^S(Rf_*(L(\mathfrak {W}^\bullet))$ as the composition of
$\mu _{L(\mathfrak {W}^\bullet)}:{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(L(\mathfrak {W}^\bullet))\rightarrow \operatorname {TH}_Y^S(Rf_*(L(\mathfrak {W}^\bullet))$ as the composition of
and
because all complexes on which ![]() $\operatorname {TH}^S$ is applied are bounded complexes.
$\operatorname {TH}^S$ is applied are bounded complexes.
Proof of Lemma 5.14 The morphism ![]() $\mu _F$ being defined, checking that it is an isomorphism is a local question on
$\mu _F$ being defined, checking that it is an isomorphism is a local question on ![]() $Y\times S$. If
$Y\times S$. If ![]() $F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ has non-zero cohomologies only in the interval
$F\in \operatorname {\mathsf {D}}^{\mathrm {b}}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$ has non-zero cohomologies only in the interval ![]() $[a,b]$, the complexes
$[a,b]$, the complexes ![]() ${}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(F)$ and
${}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(F)$ and ![]() $\operatorname {TH}_Y^S(Rf_*F)$ can have non-zero cohomologies only for indices belonging to a finite interval
$\operatorname {TH}_Y^S(Rf_*F)$ can have non-zero cohomologies only for indices belonging to a finite interval ![]() $I=[-b-m, -a+n]$ for suitable
$I=[-b-m, -a+n]$ for suitable ![]() $m,n\in \mathbb {N}$ only depending on
$m,n\in \mathbb {N}$ only depending on ![]() $\dim X$ and
$\dim X$ and ![]() $\dim Y$. Thus, it is enough to show that
$\dim Y$. Thus, it is enough to show that ![]() $\mathcal {H}^j(\mu _F)$ is an isomorphism for any
$\mathcal {H}^j(\mu _F)$ is an isomorphism for any ![]() $j\in I$. In view of Proposition 5.4, we can replace
$j\in I$. In view of Proposition 5.4, we can replace ![]() $F$ with a bounded complex
$F$ with a bounded complex ![]() $K^{\prime \bullet}=0\rightarrow K^{-N}\rightarrow K^\bullet$ with
$K^{\prime \bullet}=0\rightarrow K^{-N}\rightarrow K^\bullet$ with ![]() $N>-a+m+n$ such that
$N>-a+m+n$ such that ![]() $K^\bullet=L(\mathfrak {W}^\bullet)$ for some
$K^\bullet=L(\mathfrak {W}^\bullet)$ for some ![]() $\mathfrak {W}^\bullet\in \operatorname {\mathsf {K}}^\mathrm {b}({\mathbf {P}})$. Thus, we obtain a distinguished triangle
$\mathfrak {W}^\bullet\in \operatorname {\mathsf {K}}^\mathrm {b}({\mathbf {P}})$. Thus, we obtain a distinguished triangle ![]() $K^{-N}[N]\rightarrow L(\mathfrak {W}^\bullet)\stackrel {\tau }{\longrightarrow } F\stackrel {+1}{\longrightarrow }$, and both
$K^{-N}[N]\rightarrow L(\mathfrak {W}^\bullet)\stackrel {\tau }{\longrightarrow } F\stackrel {+1}{\longrightarrow }$, and both ![]() $\mathcal {H}^j{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(K^{-N}[N])$ and
$\mathcal {H}^j{}_{\scriptscriptstyle \mathrm {D}}f_*\operatorname {TH}_X^S(K^{-N}[N])$ and ![]() $\mathcal {H}^j\operatorname {TH}_Y^S(K^{-N}[N])$ vanish for
$\mathcal {H}^j\operatorname {TH}_Y^S(K^{-N}[N])$ vanish for ![]() $j\in I$. Hence, for any
$j\in I$. Hence, for any ![]() $j\in I$,
$j\in I$,
 \[\begin{gathered} \mathcal{H}^j{}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(F)\stackrel{\sim}{\longrightarrow}\mathcal{H}^j{}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(L(\mathfrak{W}^\bullet)),\\ \mathcal{H}^j\operatorname{TH}_Y^S(Rf_*F)\stackrel{\sim}{\longrightarrow}\mathcal{H}^j\operatorname{TH}_Y^S(Rf_*L(\mathfrak{W}^\bullet)), \end{gathered}\]
\[\begin{gathered} \mathcal{H}^j{}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(F)\stackrel{\sim}{\longrightarrow}\mathcal{H}^j{}_{\scriptscriptstyle\mathrm{D}}f_*\operatorname{TH}_X^S(L(\mathfrak{W}^\bullet)),\\ \mathcal{H}^j\operatorname{TH}_Y^S(Rf_*F)\stackrel{\sim}{\longrightarrow}\mathcal{H}^j\operatorname{TH}_Y^S(Rf_*L(\mathfrak{W}^\bullet)), \end{gathered}\]
hence we are reduced to proving that, for any ![]() $j\in \mathbb {Z}$, the morphism
$j\in \mathbb {Z}$, the morphism
(defined in Remark A.7) is an isomorphism.
Let ![]() $(y, s)\in Y\times S$. Let
$(y, s)\in Y\times S$. Let ![]() $\Omega _Y$ be a relatively compact subanalytic neighborhood of
$\Omega _Y$ be a relatively compact subanalytic neighborhood of ![]() $y$. By the assumption on
$y$. By the assumption on ![]() $f$ we can find an open relatively compact subanalytic neighborhood
$f$ we can find an open relatively compact subanalytic neighborhood ![]() $\Omega _X$ of
$\Omega _X$ of ![]() $f^{-1}\Omega _Y\cap \operatorname {Supp}_X F$. By restricting to
$f^{-1}\Omega _Y\cap \operatorname {Supp}_X F$. By restricting to ![]() $\Omega _X\times S$, we can reduce to study the case of
$\Omega _X\times S$, we can reduce to study the case of ![]() $\mathbb {C}_{W}\otimes p_X^{-1}\mathcal {O}_S$, for some
$\mathbb {C}_{W}\otimes p_X^{-1}\mathcal {O}_S$, for some ![]() $W=U\times V\in \mathcal {S}$. By the assumption on
$W=U\times V\in \mathcal {S}$. By the assumption on ![]() $f$, we have an isomorphism of functors
$f$, we have an isomorphism of functors
Thus, we have isomorphisms
 \begin{align*} Rf_*\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S)) &\stackrel{\sim}{\longrightarrow}\mathbb{R} f_*R\Gamma_{X\times V}\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes\mathcal{O}_S)\\ &\stackrel{\sim}{\longrightarrow} R\Gamma_{Y\times V}Rf_*\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes\mathcal{O}_S). \end{align*}
\begin{align*} Rf_*\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S)) &\stackrel{\sim}{\longrightarrow}\mathbb{R} f_*R\Gamma_{X\times V}\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes\mathcal{O}_S)\\ &\stackrel{\sim}{\longrightarrow} R\Gamma_{Y\times V}Rf_*\operatorname{TH}_X^S(\mathbb{C}_U\boxtimes\mathcal{O}_S). \end{align*}
Similarly,
 \begin{align*} \operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S))) &\stackrel{\sim}{\longrightarrow}\operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U)\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S)))\\ &\stackrel{\sim}{\longrightarrow}\mathbb{R}\Gamma_{Y\times V}\operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U)\boxtimes\mathcal{O}_S). \end{align*}
\begin{align*} \operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S))) &\stackrel{\sim}{\longrightarrow}\operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U)\boxtimes (\mathbb{C}_V\otimes\mathcal{O}_S)))\\ &\stackrel{\sim}{\longrightarrow}\mathbb{R}\Gamma_{Y\times V}\operatorname{TH}_Y^S(Rf_*(\mathbb{C}_U)\boxtimes\mathcal{O}_S). \end{align*}
Therefore, we are led to proving the statement for ![]() $F=\mathbb {C}_U\boxtimes \mathcal {O}_S$.
$F=\mathbb {C}_U\boxtimes \mathcal {O}_S$.
We now follow the proof of [Reference Kashiwara and SchapiraKS96, Theorem 4.4] which contains the statement in the absolute case. We decompose ![]() $f$ by the graph embedding so that we first assume that
$f$ by the graph embedding so that we first assume that ![]() $f:X\rightarrow Y$ is a closed embedding and next we treat the case of a smooth morphism.
$f:X\rightarrow Y$ is a closed embedding and next we treat the case of a smooth morphism.
Step 1. Let us assume that ![]() $f:X \rightarrow Y$ is the embedding of a closed manifold. As in the proof of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 2.4], let us start by proving the statement for
$f:X \rightarrow Y$ is the embedding of a closed manifold. As in the proof of [Reference Fiorot, Monteiro Fernandes and SabbahFMFS21, Proposition 2.4], let us start by proving the statement for ![]() $F'=\mathbb {C}_{Z\times S}\otimes p^{-1}\mathcal {O}_S$, with
$F'=\mathbb {C}_{Z\times S}\otimes p^{-1}\mathcal {O}_S$, with ![]() $Z=X\smallsetminus U$. The conclusion for
$Z=X\smallsetminus U$. The conclusion for ![]() $U$ will easily follow by functoriality, by considering the exact sequence
$U$ will easily follow by functoriality, by considering the exact sequence
We have ![]() $\operatorname {TH}^S_X(F')\simeq \Gamma _{Z\times S}(\operatorname {\mathfrak {Db}}_{X\times S})$ regarded as a
$\operatorname {TH}^S_X(F')\simeq \Gamma _{Z\times S}(\operatorname {\mathfrak {Db}}_{X\times S})$ regarded as a ![]() $\mathcal {D}_{Y_{\mathbb {R}}\times S_{\mathbb {R}}/S}$-module. We note that the local structure of distributions supported by a submanifold entail that
$\mathcal {D}_{Y_{\mathbb {R}}\times S_{\mathbb {R}}/S}$-module. We note that the local structure of distributions supported by a submanifold entail that
Then
 \begin{align*} {}_{\scriptscriptstyle\mathrm{D}}f_*\Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{X\times S})&\simeq f_*(\mathcal{D}_{Y\leftarrow X/S} \otimes_{\mathcal{D}_{X\times S/S}}\Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{X\times S}))\\ &\simeq \Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{Y\times S})\simeq \operatorname{\mathit{T}\mathcal{H}\!\mathit{om}}(f_*\mathbb{C}_{Z\times X}, \operatorname{\mathfrak{Db}}_{Y\times S})\simeq \operatorname{TH}^S_Y(f_*(\mathbb{C}_{Z\times S}\otimes p^{-1}\mathcal{O}_S)). \end{align*}
\begin{align*} {}_{\scriptscriptstyle\mathrm{D}}f_*\Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{X\times S})&\simeq f_*(\mathcal{D}_{Y\leftarrow X/S} \otimes_{\mathcal{D}_{X\times S/S}}\Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{X\times S}))\\ &\simeq \Gamma_{Z\times S}(\operatorname{\mathfrak{Db}}_{Y\times S})\simeq \operatorname{\mathit{T}\mathcal{H}\!\mathit{om}}(f_*\mathbb{C}_{Z\times X}, \operatorname{\mathfrak{Db}}_{Y\times S})\simeq \operatorname{TH}^S_Y(f_*(\mathbb{C}_{Z\times S}\otimes p^{-1}\mathcal{O}_S)). \end{align*}
Step 2. Let us now assume that ![]() $f$ is smooth and
$f$ is smooth and ![]() $f\times \operatorname {Id}_S$ is proper on the support of
$f\times \operatorname {Id}_S$ is proper on the support of ![]() $F$. The question being local we may assume as in part (ii) of the proof of [Reference Kashiwara and SchapiraKS96, Theorem 3.5] that
$F$. The question being local we may assume as in part (ii) of the proof of [Reference Kashiwara and SchapiraKS96, Theorem 3.5] that ![]() $f:X=Y\times \mathbb {R}\rightarrow \mathbb {R}$ is the projection. Recall that
$f:X=Y\times \mathbb {R}\rightarrow \mathbb {R}$ is the projection. Recall that ![]() $F\simeq \mathbb {C}_{U\times S}\otimes p_X^{-1}\mathcal {O}_S$. Let
$F\simeq \mathbb {C}_{U\times S}\otimes p_X^{-1}\mathcal {O}_S$. Let ![]() $\overline{U}=Z$. Then
$\overline{U}=Z$. Then ![]() $Z$ is closed subanalytic in
$Z$ is closed subanalytic in ![]() $X$ and the assumption entails that
$X$ and the assumption entails that ![]() $f|_{Z}$ is proper.
$f|_{Z}$ is proper.
As in step 1, we prove first the statement for ![]() $\mathbb {C}_{Z'\times S}\otimes p_X^{-1}\mathcal {O}_S$ where
$\mathbb {C}_{Z'\times S}\otimes p_X^{-1}\mathcal {O}_S$ where ![]() $Z'$ is an arbitrary closed analytic subset of
$Z'$ is an arbitrary closed analytic subset of ![]() $X$ such that
$X$ such that ![]() $f|_{Z'}$ is proper. By (3.9) of Lemma 3.6 in [Reference Kashiwara and SchapiraKS96] we may assume that for any
$f|_{Z'}$ is proper. By (3.9) of Lemma 3.6 in [Reference Kashiwara and SchapiraKS96] we may assume that for any ![]() $x\in Y$,
$x\in Y$, ![]() $Z'\cap f^{-1}(x)$ is a closed interval in
$Z'\cap f^{-1}(x)$ is a closed interval in ![]() $\mathbb {R}$ containing
$\mathbb {R}$ containing ![]() $0$. With this assumption we have
$0$. With this assumption we have
Noting that ![]() $\mathcal {D}_{Y\leftarrow X/S}$ is
$\mathcal {D}_{Y\leftarrow X/S}$ is ![]() $\mathcal {D}_{Y\times S/S}$-isomorphic to
$\mathcal {D}_{Y\times S/S}$-isomorphic to ![]() $\mathcal {D}_{Y\times S/S}/\mathcal {D}_{Y\times S/S} \partial _t$, where
$\mathcal {D}_{Y\times S/S}/\mathcal {D}_{Y\times S/S} \partial _t$, where ![]() $t$ is the coordinate in
$t$ is the coordinate in ![]() $\mathbb {R}$, the result follows by the exact sequence
$\mathbb {R}$, the result follows by the exact sequence
proved in [Reference KashiwaraKas84, Lemma 4.5]. The isomorphism for ![]() $U$ follows by functoriality considering the exact sequence
$U$ follows by functoriality considering the exact sequence
Remark A.8 In order to prove that the morphism ![]() $\tau _F:L\pi ^*R\rho _{S*}(F)\rightarrow R\rho _{S'*}L\pi ^*(F)$ of Lemma 5.7 is an isomorphism for any
$\tau _F:L\pi ^*R\rho _{S*}(F)\rightarrow R\rho _{S'*}L\pi ^*(F)$ of Lemma 5.7 is an isomorphism for any ![]() $F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, we may use the same argument of Lemma 5.14 to reduce to the case
$F\in \operatorname {\mathsf {D}}^\mathrm {b}_{{\mathbb {R} {-c}}}(p_X^{-1}\mathcal {O}_S)$, we may use the same argument of Lemma 5.14 to reduce to the case ![]() $F = \mathbb {C}_{U\times V} \otimes p_X^{-1}\mathcal {O}_S$.
$F = \mathbb {C}_{U\times V} \otimes p_X^{-1}\mathcal {O}_S$.