Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-08T23:11:10.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions

Part of: Complex manifolds Homology and cohomology theories Symplectic geometry, contact geometry Differential topology

Published online by Cambridge University Press:  24 August 2023

Oliver Goertsches ,
Panagiotis Konstantis  and
Leopold Zoller
Oliver Goertsches
Affiliation:
Philipps-Universität Marburg, Hans-Meerwein-Straße 6, D-35043 Marburg, Germany [email protected]
Panagiotis Konstantis
Affiliation:
Mathematik und Informatik, Philipps-Universität Marburg, Hans-Meerwein-Straße 6, D-35043 Marburg, Germany [email protected]
Leopold Zoller
Affiliation:
Ludwig-Maximilians-Universität München, Theresienstr. 39, D-80333 München, Germany [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We classify fibrations of abstract 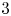$3$-regular GKM graphs over 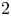$2$-regular ones, and show that all fibrations satisfying the known necessary conditions for realizability are, in fact, realized as the projectivization of equivariant complex rank-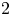$2$ vector bundles over quasitoric 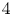$4$-manifolds or 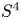$S^4$. We investigate the existence of invariant (stable) almost complex, symplectic, and Kähler structures on the total space. In this way, we obtain infinitely many Kähler manifolds with Hamiltonian non-Kähler actions in dimension 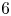$6$ with prescribed one-skeleton, in particular with a prescribed number of isolated fixed points.

Keywords

equivariant topologyGKM fibrationsrealization of GKM graphscohomogeneity one manifoldsHamiltonian non-Kähler actionsequivariant geometric structuresequivariant obstruction theory

MSC classification

Primary: 57R91: Equivariant algebraic topology of manifolds 55N91: Equivariant homology and cohomology 53D05: Symplectic manifolds, general 32Q15: Kähler manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 10 , October 2023 , pp. 2149 - 2190
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseevsky, A. V. and Alekseevsky, D. V., Riemannian $G$-manifold with one-dimensional orbit space, Ann. Global Anal. Geom. 11 (1993), 197–211.CrossRefGoogle Scholar
Bott, R. and Tu, L. W., Differential forms in algebraic topology, Graduate Texts in Mathematics, vol. 82 (Springer, New York–Berlin, 1982).CrossRefGoogle Scholar
Bredon, G. E., Introduction to compact transformation groups, Pure and Applied Mathematics, vol. 46 (Academic Press, New York–London, 1972).Google Scholar
Buchstaber, V. M. and Panov, T. E., Toric topology, Mathematical Surveys and Monographs, vol. 204 (American Mathematical Society, Providence, RI, 2015).CrossRefGoogle Scholar
Choi, S. and Park, S., Projective bundles over toric surfaces, Internat. J. Math. 27 (2016), 1650032.CrossRefGoogle Scholar
Davis, M. W. and Januszkiewicz, T., Convex polytopes, Coxeter orbifolds and torus actions, Duke Math. J. 62 (1991), 417–451.CrossRefGoogle Scholar
Delzant, T., Hamiltoniens périodiques et images convexes de l'application moment, Bull. Soc. Math. France 116 (1988), 315–339.CrossRefGoogle Scholar
Eschenburg, J.-H., Freie isometrische Aktionen auf kompakten Lie-Gruppen mit positiv gekrümmten Orbiträumen, Schriftenreihe des Mathematischen Instituts der Universität Münster, 2. Serie, vol. 32 (Universität Münster, Mathematisches Institut, Münster, 1984).Google Scholar
Eschenburg, J.-H., Inhomogeneous spaces of positive curvature, Differential Geom. Appl. 2 (1992), 123–132.CrossRefGoogle Scholar
Franz, M. and Yamanaka, H., Graph equivariant cohomological rigidity for GKM graphs, Proc. Japan Acad. Ser. A Math. Sci. 95 (2019), 107–110.CrossRefGoogle Scholar
Galaz-García, F. and Zarei, M., Cohomogeneity one topological manifolds revisited, Math. Z. 288 (2018), 829–853.CrossRefGoogle Scholar
Goertsches, O., Konstantis, P. and Zoller, L., GKM theory and Hamiltonian non-Kähler actions in dimension $6$, Preprint (2019), arXiv:1903.11684.Google Scholar
Goertsches, O., Konstantis, P. and Zoller, L., Symplectic and Kähler structures on biquotients, J. Symplectic Geom. 18 (2020), 791–813.CrossRefGoogle Scholar
Goertsches, O. and Wiemeler, M., Non-negatively curved GKM orbifolds, Math. Z. 300 (2022), 2007–2036.CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Equivariant cohomology, Koszul duality, and the localization theorem, Invent. Math. 131 (1998), 25–83.CrossRefGoogle Scholar
Guillemin, V., Sabatini, S. and Zara, C., Cohomology of GKM fiber bundles, J. Algebraic Combin. 35 (2012), 19–59.10.1007/s10801-011-0292-6CrossRefGoogle Scholar
Guillemin, V. and Sternberg, S., Symplectic techniques in physics (Cambridge University Press, Cambridge, 1984).Google Scholar
Guillemin, V. and Zara, C., Equivariant de Rham theory and graphs, Asian J. Math. 3 (1999), 49–76.CrossRefGoogle Scholar
Guillemin, V. and Zara, C., 1-skeleta, Betti numbers, and equivariant cohomology, Duke Math. J. 107 (2001), 283–349.CrossRefGoogle Scholar
Huybrechts, D., An introduction, in Complex geometry, Universitext (Springer, Berlin, 2005).Google Scholar
Karshon, Y., Periodic Hamiltonian flows on four-dimensional manifolds, Mem. Amer. Math. Soc. 141 (1999).Google Scholar
Karshon, Y. and Tolman, S., Complete invariants for Hamiltonian torus actions with two dimensional quotients, J. Symplectic Geom. 2 (2003), 25–82.CrossRefGoogle Scholar
Kustarev, A. A., Equivariant almost complex structures on quasitoric manifolds, Tr. Mat. Inst. Steklova 266 (2009), 140–148.Google Scholar
Lashof, R. K., Equivariant bundles, Illinois J. Math. 26 (1982), 257–271.CrossRefGoogle Scholar
Lefschetz, S., L'analysis situs et la géométrie algébrique (Gauthier-Villars, Paris, 1950).Google Scholar
Masuda, M. and Panov, T., On the cohomology of torus manifolds, Osaka J. Math. 43 (2006), 711–746.Google Scholar
Mostert, P. S., On a compact Lie group acting on a manifold, Ann. of Math. (2) 65 (1957), 447–455.CrossRefGoogle Scholar
Okonek, C. and Van de Ven, A., Cubic forms and complex $3$-folds, Enseign. Math. (2) 41 (1995), 297–333.Google Scholar
Schwarzenberger, R. L. E., Vector bundles on algebraic surfaces, Proc. Lond. Math. Soc. (3) 11 (1961), 601–622.CrossRefGoogle Scholar
Serre, J.-P., Géométrie algébrique et géométrie analytique, Ann. Inst. Fourier (Grenoble) 6 (1955–1956), 1–42.CrossRefGoogle Scholar
Tolman, S., Examples of non-Kähler Hamiltonian torus actions, Invent. Math. 131 (1998), 299–310.CrossRefGoogle Scholar
tom Dieck, T., Faserbündel mit Gruppenoperation, Arch. Math. (Basel) 20 (1969), 136–143.CrossRefGoogle Scholar
tom Dieck, T., Transformation groups, De Gruyter Studies in Mathematics, vol. 8 (Walter de Gruyter, Berlin, 1987).CrossRefGoogle Scholar
Voisin, C., Hodge theory and complex algebraic geometry. I, English edition, Cambridge Studies in Advanced Mathematics, vol. 76 (Cambridge University Press, Cambridge, 2007), translated from the French by Leila Schneps.Google Scholar
Wasserman, A. G., Equivariant differential topology, Topology 8 (1969), 127–150.CrossRefGoogle Scholar
Woodward, C., Multiplicity-free Hamiltonian actions need not be Kähler, Invent. Math. 131 (1998), 311–319.CrossRefGoogle Scholar