Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T01:55:21.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational rigidity for ${E}_{8}(p)$

Part of: Field extensions Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  17 July 2014

Robert Guralnick  and
Gunter Malle
Robert Guralnick
Affiliation:
Department of Mathematics, University of Southern California, Los Angeles, CA 90089-2532, USA email [email protected]
Gunter Malle
Affiliation:
FB Mathematik, TU Kaiserslautern, Postfach 3049, 67653 Kaiserslautern, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

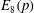We prove the existence of certain rationally rigid triples in 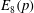${E}_{8}(p)$ for good primes 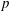$p$ (i.e. 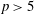$p>5$) thereby showing that these groups occur as Galois groups over the field of rational numbers. We show that these triples arise from rigid triples in the algebraic group and prove that they generate an interesting subgroup in characteristic zero. As a byproduct of the proof, we derive a remarkable symmetry between the character table of a finite reductive group and that of its dual group. We also give a short list of possible overgroups of regular unipotent elements in simple exceptional groups.

Keywords

inverse Galois problemrigidityLie primitive subgroupsregular unipotent elements

MSC classification

Secondary: 12F12: Inverse Galois theory 20C33: Representations of finite groups of Lie type 20E28: Maximal subgroups
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 10 , October 2014 , pp. 1679 - 1702
Copyright
© The Author(s) 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aschbacher, M., The maximal subgroups of ${E}_{6}$, Preprint (1991).Google Scholar
Carter, R. W., Finite groups of Lie type. Conjugacy classes and complex characters, Wiley Classics Library (John Wiley and Sons, Chichester, 1993).Google Scholar
Cooperstein, B. N., Maximal subgroups of G 2(2n), J. Algebra 70 (1981), 23–36.Google Scholar
Curtis, C., Kantor, W. M. and Seitz, G. M., The 2-transitive permutation representations of the finite Chevalley groups, Trans. Amer. Math. Soc. 218 (1976), 1–59.Google Scholar
Dettweiler, M. and Reiter, S., Rigid local systems and motives of type G 2. With an appendix by Michael Dettweiler and Nicholas M. Katz, Compositio Math. 146 (2010), 929–963.Google Scholar
Digne, F. and Michel, J., Representations of finite groups of Lie type, London Mathematical Society Student Texts, vol. 21 (Cambridge University Press, Cambridge, 1991).Google Scholar
DiMuro, J., On prime power order elements of general linear groups, J. Algebra 367 (2012), 222–236.Google Scholar
Feit, W. and Fong, P., Rational rigidity of G 2(p) for any prime p > 5, in Proceedings of the Rutgers group theory year 1983–1984 (New Brunswick, NJ) (Cambridge University Press, Cambridge, 1985), 323–326.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The classification of the finite simple groups. Number 3, Mathematical Surveys and Monographs (American Mathematical Society, Providence, RI, 1998).Google Scholar
Guralnick, R. M., Lübeck, F. and Yu, J., Rational rigidity for ${F}_{4}(p)$, Preprint (2014).Google Scholar
Guralnick, R. M., Penttila, T., Praeger, C. and Saxl, J., Linear groups with orders having certain large prime divisors, Proc. Lond. Math. Soc. (3) 78 (1999), 167–214.Google Scholar
Guralnick, R. M. and Tiep, P., Lifting in Frattini covers and a characterization of finite solvable groups, J. Reine Angew. Math., published online (2013), doi:10.1515/crelle-2013-0085.Google Scholar
Jones, W. and Parshall, B., On the 1-cohomology of finite groups of Lie type, in Proceedings of the conference on finite groups (University of Utah, Park City, 1975) (Academic Press, New York, 1976), 313–328.Google Scholar
Kleidman, P. B., The maximal subgroups of the Chevalley groups G 2(q) with q odd, the Ree groups 2G 2(q), and their automorphism groups, J. Algebra 117 (1988), 30–71.Google Scholar
Lawther, R., Jordan block sizes of unipotent elements in exceptional algebraic groups, Comm. Algebra 23 (1995), 4125–4156.CrossRefGoogle Scholar
Lawther, R., Unipotent classes in maximal subgroups of exceptional algebraic groups, J. Algebra 322 (2009), 270–293.Google Scholar
Lawther, R., Sublattices generated by root differences, J. Algebra, to appear.Google Scholar
Liebeck, M. W., Litterick, A. J. and Marion, C., A rigid triple of conjugacy classes in G 2, J. Group Theory 41 (2011), 31–35.Google Scholar
Liebeck, M. W. and Seitz, G. M., On finite subgroups of exceptional algebraic groups, J. Reine Angew. Math. 515 (1999), 25–72.Google Scholar
Liebeck, M. W. and Seitz, G. M., A survey of maximal subgroups of exceptional groups of Lie type, in Groups, combinatorics and geometry (Durham, 2001) (World Scientific, River Edge, NJ, 2003), 139–146.Google Scholar
Lübeck, F., Small degree representations of finite Chevalley groups in defining characteristic, LMS J. Comput. Math. 4 (2011), 135–169.Google Scholar
Lusztig, G., Character sheaves V, Adv. Math. 61 (1986), 103–155.Google Scholar
Lusztig, G., On the representations of reductive groups with disconnected centre, Astérisque 168 (1988), 157–166.Google Scholar
Magaard, K., The maximal subgroups of ${F}_{4}(F)$ where $F$ is a finite or algebraically closed field of characteristic $\neq 2,3$, PhD thesis, Caltech (1990).Google Scholar
Malle, G. and Matzat, B. H., Inverse Galois theory, Springer Monographs in Mathematics (Springer, Berlin, 1999).Google Scholar
Malle, G. and Testerman, D., Linear algebraic groups and finite groups of Lie type, Cambridge Studies in Advanced Mathematics, vol. 133 (Cambridge University Press, Cambridge, 2011).Google Scholar
McNinch, G., Dimensional criteria for semisimplicity of representations, J. Lond. Math. Soc. (2) 76 (1998), 95–149.Google Scholar
Michel, J., The GAP-part of the Chevie system. GAP 3-package available for download from http://people.math.jussieu.fr/∼jmichel/chevie/chevie.html.Google Scholar
Saxl, J. and Seitz, G. M., Subgroups of algebraic groups containing regular unipotent elements, J. Lond. Math. Soc. (2) 55 (1997), 370–386.Google Scholar
Scott, L. L., Matrices and cohomology, Ann. of Math. (2) 105 (1977), 473–492.Google Scholar
Seitz, G. M. and Testerman, D., Extending morphisms from finite to algebraic groups, J. Algebra 131 (1990), 559–574.Google Scholar
Seitz, G. M. and Testerman, D., Subgroups of type A 1containing semiregular unipotent elements, J. Algebra 196 (1997), 595–619.Google Scholar
Serre, J. -P., Galois cohomology, Springer Monographs in Mathematics (Springer, Berlin, 2002), corrected reprint of the 1997 English edition.Google Scholar
Sin, P., On the 1-cohomology of the groups G 2(2n), Comm. Algebra 20 (1992), 2653–2662.Google Scholar
Sin, P., Extensions of simple modules for G 2(3n) and 2G 2(3m), Proc. Lond. Math. Soc. (2) 66 (1993), 327–357.Google Scholar
Spaltenstein, N., On the generalized Springer correspondence for exceptional groups, in Algebraic groups and related topics (Kyoto/Nagoya, 1983), Advanced Studies in Pure Mathematics, vol. 6 (North-Holland, Amsterdam, 1985), 317–338.Google Scholar
Suprunenko, I., The minimal polynomials of unipotent elements in irreducible representations of the classical groups in odd characteristic, Memoirs of the American Mathematical Society, vol. 200, no. 939 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Thompson, J. G., Rational rigidity of G 2(5), in Proceedings of the Rutgers group theory year, 1983–1984 (New Brunswick, NJ, 1983–1984) (Cambridge University Press, Cambridge, 1985), 321–322.Google Scholar
Weigel, T., On the profinite completion of arithmetic groups of split type, in Lois d’algèbres et variétés algébriques (Colmar, 1991), Travaux en Cours, vol. 50 (Hermann, Paris, 1996), 79–101.Google Scholar
Yun, Z., Motives with exceptional Galois groups and the inverse Galois problem, Invent. Math. 196 (2014), 267–337.Google Scholar
Zywina, D., The inverse Galois problem for ${\text{L}}_{2}({\mathbb{F}}_{p})$, Preprint (2013), arXiv:1303.3646.Google Scholar