Article contents
Rational cobordisms and integral homology
Published online by Cambridge University Press: 29 October 2020
Abstract
We consider the question of when a rational homology 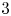 $3$-sphere is rational homology cobordant to a connected sum of lens spaces. We prove that every rational homology cobordism class in the subgroup generated by lens spaces is represented by a unique connected sum of lens spaces whose first homology group injects in the first homology group of any other element in the same class. As a first consequence, we show that several natural maps to the rational homology cobordism group have infinite-rank cokernels. Further consequences include a divisibility condition between the determinants of a connected sum of
$3$-sphere is rational homology cobordant to a connected sum of lens spaces. We prove that every rational homology cobordism class in the subgroup generated by lens spaces is represented by a unique connected sum of lens spaces whose first homology group injects in the first homology group of any other element in the same class. As a first consequence, we show that several natural maps to the rational homology cobordism group have infinite-rank cokernels. Further consequences include a divisibility condition between the determinants of a connected sum of 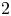 $2$-bridge knots and any other knot in the same concordance class. Lastly, we use knot Floer homology combined with our main result to obstruct Dehn surgeries on knots from being rationally cobordant to lens spaces.
$2$-bridge knots and any other knot in the same concordance class. Lastly, we use knot Floer homology combined with our main result to obstruct Dehn surgeries on knots from being rationally cobordant to lens spaces.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s) 2020
References
- 3
- Cited by



