Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T01:46:52.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank 3 quadratic generators of Veronese embeddings

Part of: Algebraic geometry: Foundations Special varieties Commutative algebra: Homological methods Projective and enumerative geometry

Published online by Cambridge University Press:  02 August 2021

Kangjin Han ,
Wanseok Lee ,
Hyunsuk Moon  and
Euisung Park
Kangjin Han
Affiliation:
School of Undergraduate Studies, Daegu-Gyeongbuk Institute of Science & Technology (DGIST), Daegu42988, Republic of [email protected]
Wanseok Lee
Affiliation:
Department of Applied Mathematics, Pukyong National University, Busan608-737, Republic of [email protected]
Hyunsuk Moon
Affiliation:
Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology, Daejeon34141, Republic of [email protected]
Euisung Park
Affiliation:
Department of Mathematics, Korea University, Seoul136-701, Republic of [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 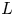$L$ be a very ample line bundle on a projective scheme 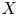$X$ defined over an algebraically closed field 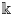$\Bbbk$ with 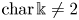${\rm char}\,\Bbbk \neq 2$. We say that 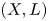$(X,L)$ satisfies property 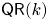$\mathsf {QR}(k)$ if the homogeneous ideal of the linearly normal embedding 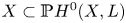$X \subset {\mathbb {P}} H^{0} (X,L)$ can be generated by quadrics of rank less than or equal to 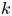$k$. Many classical varieties, such as Segre–Veronese embeddings, rational normal scrolls and curves of high degree, satisfy property 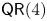$\mathsf {QR}(4)$. In this paper, we first prove that if 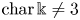${\rm char}\,\Bbbk \neq 3$ then 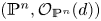$({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (d))$ satisfies property 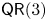$\mathsf {QR}(3)$ for all 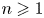$n \geqslant 1$ and 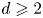$d \geqslant 2$. We also investigate the asymptotic behavior of property 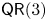$\mathsf {QR}(3)$ for any projective scheme. Specifically, we prove that (i) if 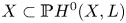$X \subset {\mathbb {P}} H^{0} (X,L)$ is 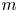$m$-regular then 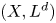$(X,L^{d} )$ satisfies property 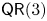$\mathsf {QR}(3)$ for all 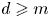$d \geqslant m$, and (ii) if 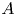$A$ is an ample line bundle on 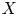$X$ then 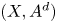$(X,A^{d} )$ satisfies property 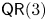$\mathsf {QR}(3)$ for all sufficiently large even numbers 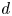$d$. These results provide affirmative evidence for the expectation that property 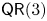$\mathsf {QR}(3)$ holds for all sufficiently ample line bundles on 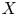$X$, as in the cases of Green and Lazarsfeld's condition 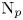$\mathrm {N}_p$ and the Eisenbud–Koh–Stillman determininantal presentation in Eisenbud et al. [Determinantal equations for curves of high degree, Amer. J. Math. 110 (1988), 513–539]. Finally, when 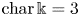${\rm char}\,\Bbbk = 3$ we prove that 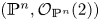$({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (2))$ fails to satisfy property 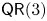$\mathsf {QR}(3)$ for all 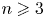$n \geqslant 3$.

Keywords

low rank quadricsVeronese varietyVeronese re-embeddingdeterminantal presentationproperty

MSC classification

Primary: 13D02: Syzygies, resolutions, complexes 14A25: Elementary questions 14N05: Projective techniques 14M12: Determinantal varieties 14M17: Homogeneous spaces and generalizations
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 9 , September 2021 , pp. 2001 - 2025
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E. and Harris, J., Canonical curves and quadrics of rank 4, Compos. Math. 43 (1981), 145–179.Google Scholar
Bernardi, A., Ideals of varieties parameterized by certain symmetric tensors, J. Pure Appl. Algebra 212 (2008), 1542–1559.CrossRefGoogle Scholar
Choi, Y. and Park, E., On higher syzygies of ruled surfaces III, J. Pure Appl. Algebra 219 (2015), 4653–4666.CrossRefGoogle Scholar
Eisenbud, D., The geometry of syzygies: a second course in commutative algebra and algebraic geometry (Springer, New York, 2005).Google Scholar
Eisenbud, D., Green, M., Hulek, K. and Popescu, S., Restriction linear syzygies: algebra and geometry, Compos. Math. 141 (2005), 1460–1478.CrossRefGoogle Scholar
Eisenbud, D., Koh, J. and Stillman, M., Determinantal equations for curves of high degree, Amer. J. Math. 110 (1988), 513–539.CrossRefGoogle Scholar
Ein, L. and Lazarsfeld, R., Syzygies and Koszul cohomology of smooth projective varieties of arbitrary dimension, Invent. Math. 111 (1993), 51–67.CrossRefGoogle Scholar
Gallego, F. J. and Purnaprajna, B. P., Projective normality and syzygies of algebraic surfaces, J. Reine Angew. Math. 506 (1999), 145–180.CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E., Macaulay 2: a software system for research in algebraic geometry, http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Giraldo, L., Lopez, A. F. and Muñoz, R., On the projective normality of Enriques surfaces. With an appendix by Lopez and Alessandro Verra, Math. Ann. 324 (2002), 135–158.CrossRefGoogle Scholar
Green, M. L., Quadrics of rank four in the ideal of a canonical curve, Invent. Math. 75 (1984), 85–104.CrossRefGoogle Scholar
Green, M. L., Koszul cohomology and the geometry of projective varieties I, J. Differential Geom. 19 (1984), 125–171.CrossRefGoogle Scholar
Green, M. L., Koszul cohomology and the geometry of projective varieties II, J. Differential Geom. 20 (1984), 279–289.CrossRefGoogle Scholar
Green, M. L. and Lazarsfeld, R., Some results on the syzygies of finite sets and algebraic curves, Compos. Math. 67 (1988), 301–314.Google Scholar
Hà, H. T., Box-shaped matrices and the defining ideal of certain blow up surface, J. Pure Appl. Algebra 167 (2002), 203–224.CrossRefGoogle Scholar
Harris, J., Algebraic geometry. A first course, Graduate Texts in Mathematics, vol. 133 (Springer, New York, 1992).CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).CrossRefGoogle Scholar
Inamdar, S. P., On syzygies of projective varieties, Pacific J. Math. 177 (1997), 71–75.CrossRefGoogle Scholar
Kasman, A., Pedings, K., Reiszl, A. and Shiota, T., Universality of rank $6$ Plucker relations and Grassmann cone preserving maps, Proc. Amer. Math. Soc. 136 (2008), 77–87.CrossRefGoogle Scholar
Mumford, D., Varieties defined by quadratic equations, in Questions on algebraic varieties (C.I.M.E., III) (Ciclo, Varenna, 1969) (Edizioni Cremonese, Rome, 1970), 29–100.Google Scholar
Pareschi, G., Syzygies of abelian varieties, J. Amer. Math. Soc. 13 (2000), 51–664.CrossRefGoogle Scholar
Petri, K., Über die invariante Darstellung algebraischer Funktionen, Math. Ann. 88 (1923), 243–289.CrossRefGoogle Scholar
Pucci, M., The Veronese variety and Catalecticant matrices, J. Algebra 202 (1998), 72–95.CrossRefGoogle Scholar
Saint-Donat, B., Sur les èquations définisant une courbe algebrique, C. R. Acad. Sci. Paris 274 (1972), 324–327.Google Scholar
Saint-Donat, B., On Petri's analysis of the linear system of quadrics through a canonical curve, Math. Ann. 206 (1973), 157–175.CrossRefGoogle Scholar
Sidman, J. and Smith, G., Linear determinantal equations for all projective schemes, Algebra Number Theory 5 (2011), 1041–1061.CrossRefGoogle Scholar