Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T05:57:50.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Random walks on projective spaces

Part of: Markov processes Lie groups

Published online by Cambridge University Press:  17 July 2014

Yves Benoist  and
Jean-François Quint
Yves Benoist
Affiliation:
CNRS – Université Paris-Sud, Bat. 425, 91405 Orsay, France email [email protected]
Jean-François Quint
Affiliation:
CNRS – Université Paris-Nord, LAGA, 93430 Villetaneuse, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

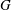Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a connected real semisimple Lie group, 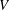$V$ be a finite-dimensional representation of 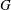$G$ and 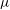$\mu $ be a probability measure on 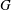$G$ whose support spans a Zariski-dense subgroup. We prove that the set of ergodic 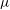$\mu $-stationary probability measures on the projective space 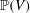$\mathbb{P}(V)$ is in one-to-one correspondence with the set of compact 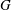$G$-orbits in 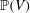$\mathbb{P}(V)$. When 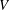$V$ is strongly irreducible, we prove the existence of limits for the empirical measures. We prove related results over local fields as the finiteness of the set of ergodic 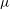$\mu $-stationary measures on the flag variety of 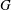$G$.

Keywords

semisimple groupflag varietystationary measureMarkov chain

MSC classification

Secondary: 22E40: Discrete subgroups of Lie groups 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 9 , September 2014 , pp. 1579 - 1606
Copyright
© The Author(s) 2014 

References

Abels, H., Margulis, G. and Soifer, G., Semigroups containing proximal linear maps, Israel J. Math. 91 (1995), 1–30.Google Scholar
Benoist, Y., Propriétés asymptotiques des groupes linéaires, Geom. Funct. Anal. 7 (1997), 1–47.Google Scholar
Benoist, Y., Convexes divisibles III, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 793–832.Google Scholar
Benoist, Y. and Quint, J.-F., Introduction to random walks on homogeneous spaces, Tenth Takagi Lecture, Japan. J. Math. 7 (2012), 135–166.Google Scholar
Benoist, Y. and Quint, J.-F., (2013), Random walks on reductive groups, Preprint (2013), available at: http://www.math.u-psud.fr/∼benoist/prepubli/13walk.pdf.Google Scholar
Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126 (Springer, New York, 1991).Google Scholar
Bougerol, P. and Lacroix, J., Products of Random Matrices with Applications to Schrödinger Operators, Progress in Probability, vol. 8 (Birkhäuser, Basel, 1985).Google Scholar
Breiman, L., The strong law of large numbers for a class of Markov chains, Ann. Math. Statist. 31 (1960), 801–803.CrossRefGoogle Scholar
Eisner, T., Farkas, B., Haase, M. and Nagel, R., Ergodic theory—an operator theoretic approach, in Tulka Internet Seminar (2009), available at http://www.math.ist.utl.pt/∼czaja/ISEM/internetseminar200809.pdf.Google Scholar
Furstenberg, H., Strict ergodicity and transformation of the torus, Amer. J. Math. 83 (1961), 573–601.Google Scholar
Furstenberg, H., Noncommuting random products, Trans. Amer. Math. Soc. 108 (1963), 377–428.Google Scholar
Furstenberg, H., Stiffness of group actions, Tata Inst. Fund. Res. Stud. Math. 14 (1998), 105–117.Google Scholar
Goldsheid, I. and Margulis, G., Lyapunov indices of a product of random matrices, Russian Math. Surveys 44 (1989), 11–81.Google Scholar
Guivarc’h, Y, On the spectrum of a large subgroup of a semi-simple group, J. Mod. Dyn. 2 (2008), 15–42.Google Scholar
Guivarc’h, Y. and Raugi, A., Frontière de Furstenberg, propriété de contraction et théorèmes de convergence, Z. Wahrsch. Verw. Gebiete 69 (1985), 187–242.Google Scholar
Guivarc’h, Y. and Raugi, A., Actions of large semigroups and random walks on isometric extensions of boundaries, Ann. Sci. Éc Norm. Supér. (4) 40 (2007), 209–249.Google Scholar
Quint, J.-F., Mesures de Patterson–Sullivan en rang supérieur, Geom. Funct. Anal. 12 (2002), 776–809.Google Scholar
Quint, J.-F., Groupes de Schottky et comptage, Ann. Inst. Fourier. (Grenoble) 55 (2005), 373–429.Google Scholar
Raghunathan, M., Discrete subgroups of Lie groups (Springer, New York, 1972).Google Scholar
Raugi, A., Théorie spectrale d’un opérateur de transition sur un espace métrique compact, Ann. Inst. Henri Poincaré Probab. Stat. 28 (1992), 281–309.Google Scholar
Rosenblatt, M., Equicontinuous Markov operators, Teor. Veroyatn. Primen. 9 (1964), 205–222.Google Scholar
Rudin, W., Functional Analysis (McGraw-Hill, 1973).Google Scholar
Spitzer, F., Principles of Random Walk, Graduate Texts in Mathematics, vol. 34 (Springer, New York, 1964).Google Scholar