Published online by Cambridge University Press: 01 November 2007
An extension of a result of Sela shows that if Γ is a torsion-free word hyperbolic group, then the only homomorphisms Γ→Γ with finite-index image are the automorphisms. It follows from this result and properties of quasiregular mappings, that if M is a closed Riemannian n-manifold with negative sectional curvature (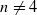 ), then every quasiregular mapping f:M→M is a homeomorphism. In the constant-curvature case the dimension restriction is not necessary and Mostow rigidity implies that f is homotopic to an isometry. This is to be contrasted with the fact that every such manifold admits a non-homeomorphic light open self-mapping. We present similar results for more general quotients of hyperbolic space and quasiregular mappings between them. For instance, we establish that besides covering projections there are no π1-injective proper quasiregular mappings f:M→N between hyperbolic 3-manifolds M and N with non-elementary fundamental group.
), then every quasiregular mapping f:M→M is a homeomorphism. In the constant-curvature case the dimension restriction is not necessary and Mostow rigidity implies that f is homotopic to an isometry. This is to be contrasted with the fact that every such manifold admits a non-homeomorphic light open self-mapping. We present similar results for more general quotients of hyperbolic space and quasiregular mappings between them. For instance, we establish that besides covering projections there are no π1-injective proper quasiregular mappings f:M→N between hyperbolic 3-manifolds M and N with non-elementary fundamental group.
This material is based upon work supported by the National Science Foundation under Grants No. 0200752 and 0457291, the N.Z. Marsden Fund and the NZIMA. The first author is supported by a Royal Society Wolfson Merit Award. He was also the Forder Lecturer during the completion of this work and would like to thank the London Mathematical Society and the New Zealand Mathematical Society for their support.