Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cave, Chris
and
Dreesen, Dennis
2016.
Embeddings of locally compact hyperbolic groups into L-spaces.
Topology and its Applications,
Vol. 214,
Issue. ,
p.
66.
Alvarez, Aurélien
and
Lafforgue, Vincent
2017.
Actions affines isométriques propres des groupes hyperboliques sur des espaces ℓp.
Expositiones Mathematicae,
Vol. 35,
Issue. 1,
p.
103.
Emerson, Heath
and
Nica, Bogdan
2018.
K-homological finiteness and hyperbolic groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2018,
Issue. 745,
p.
189.
Druţu, Cornelia
and
Nowak, Piotr W.
2019.
Kazhdan projections, random walks and ergodic theorems.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 754,
p.
49.
Druţu, Cornelia
and
Mackay, John M.
2019.
Random groups, random graphs and eigenvalues of p-Laplacians.
Advances in Mathematics,
Vol. 341,
Issue. ,
p.
188.
Nica, Bogdan
2019.
Two applications of strong hyperbolicity.
Kyoto Journal of Mathematics,
Vol. 59,
Issue. 2,
Chatterji, Indira
and
Dahmani, François
2020.
Proper actions on ℓ p -spaces for relatively hyperbolic groups.
Annales Henri Lebesgue,
Vol. 3,
Issue. ,
p.
35.
Lavy, Omer
and
Olivier, Baptiste
2021.
Fixed-point spectrum for group actions by affine isometries on L p -spaces.
Annales de l'Institut Fourier,
Vol. 71,
Issue. 1,
p.
1.
TANAKA, RYOKICHI
2021.
Topological flows for hyperbolic groups.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 11,
p.
3474.
Boyer, Adrien
2021.
Some spherical functions on hyperbolic groups.
Journal of Topology and Analysis,
Vol. 13,
Issue. 04,
p.
1125.
Dahmani, François
Hagen, Mark
and
Sisto, Alessandro
2021.
Dehn filling Dehn twists.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 151,
Issue. 1,
p.
28.
Marrakchi, Amine
and
de la Salle, Mikael
2023.
Isometric actions on Lp-spaces: dependence on the value of p.
Compositio Mathematica,
Vol. 159,
Issue. 6,
p.
1300.
Behrstock, Jason
Hagen, Mark
Martin, Alexandre
and
Sisto, Alessandro
2024.
A combinatorial take on hierarchical hyperbolicity and applications to quotients of mapping class groups.
Journal of Topology,
Vol. 17,
Issue. 3,
Boyer, Adrien
and
Paoli, Jean-Martin
2024.
Riesz operators and L-boundary representations for hyperbolic groups.
Journal of Functional Analysis,
Vol. 287,
Issue. 12,
p.
110650.
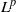 $L^p$-spaces
$L^p$-spaces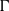 $\G $ admits a proper affine isometric action on
$\G $ admits a proper affine isometric action on  $L^p(\bd \G \times \bd \G )$, where
$L^p(\bd \G \times \bd \G )$, where 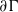 $\bd \G $ denotes the boundary of
$\bd \G $ denotes the boundary of 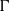 $\G $ and
$\G $ and 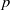 $p$ is large enough. Our construction involves a
$p$ is large enough. Our construction involves a 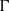 $\G $-invariant measure on
$\G $-invariant measure on 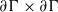 $\bd \G \times \bd \G $ analogous to the Bowen–Margulis measure from the
$\bd \G \times \bd \G $ analogous to the Bowen–Margulis measure from the 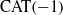 ${\rm CAT}(-1)$ setting, as well as a geometric, Busemann-type cocycle. We also deduce that
${\rm CAT}(-1)$ setting, as well as a geometric, Busemann-type cocycle. We also deduce that 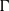 $\G $ admits a proper affine isometric action on the first
$\G $ admits a proper affine isometric action on the first 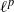 $\ell ^p$-cohomology group
$\ell ^p$-cohomology group 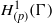 $H^1_{(p)}(\G )$ for large enough
$H^1_{(p)}(\G )$ for large enough 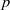 $p$.
$p$.

