Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-24T10:45:54.674Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Einstein metrics with 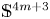$\mathbb {S}^{4m+3}$ as the principal orbit

Part of: Global differential geometry

Published online by Cambridge University Press:  08 April 2024

Hanci Chi Open the ORCID record for Hanci Chi [Opens in a new window]
Hanci Chi*
Affiliation:
Department of Foundational Mathematics, Xi'an Jiaotong–Liverpool University, Suzhou 215123, PR China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that there exists at least one positive Einstein metric on 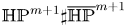$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for 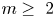$m\geq ~2$. Based on the existence of the first Einstein metric, we give a criterion to check the existence of a second Einstein metric on 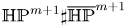$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$. We also investigate the existence of cohomogeneity-one positive Einstein metrics on 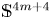$\mathbb {S}^{4m+4}$ and prove the existence of a non-standard Einstein metric on 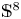$\mathbb {S}^8$.

Keywords

Einstein metriccohomogeneity-one metric

MSC classification

Primary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 5 , May 2024 , pp. 1004 - 1040
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is supported by NSFC (No. 12071489, No. 12301078), the Foundation for Young Scholars of Jiangsu Province, China (BK-20220282), and XJTLU Research Development Funding (RDF-21-02-083).

References

Bérard-Bergery, L., Sur de nouvelles variétés riemanniennes d'Einstein, Institut Élie Cartan, vol. 6 (Univ. Nancy, Nancy, 1982), 1–60.Google Scholar
Böhm, C., Inhomogeneous Einstein metrics on low-dimensional spheres and other low-dimensional spaces, Invent. Math. 134 (1998), 145–176.Google Scholar
Bryant, R. L. and Salamon, S. M., On the construction of some complete metrics with exceptional holonomy, Duke Math. J. 58 (1989), 829–850.CrossRefGoogle Scholar
Chi, H., Cohomogeneity one Einstein metrics on vector bundles, PhD thesis, McMaster University (2019).Google Scholar
Chi, H., Einstein metrics of cohomogeneity one with $\mathbb {S}^{4m+3}$ as principal orbit, Comm. Math. Phys. 386 (2021), 1011–1049.CrossRefGoogle Scholar
Coddington, E. A. and Levinson, N., Theory of ordinary differential equations (McGraw-Hill, New York, 1955).Google Scholar
Dancer, A. S., Hall, S. J. and Wang, M. Y., Cohomogeneity one shrinking Ricci solitons: an analytic and numerical study, Asian J. Math. 17 (2013), 33–62.CrossRefGoogle Scholar
Dancer, A. S. and Wang, M. Y., Non-Kähler expanding Ricci solitons, Int. Math. Res. Not. IMRN 2009 (2009), 1107–1133.CrossRefGoogle Scholar
Eschenburg, J.-H. and Wang, M. Y., The initial value problem for cohomogeneity one Einstein metrics, J. Geom. Anal. 10 (2000), 109–137.CrossRefGoogle Scholar
Foscolo, L. and Haskins, M., New G$_2$-holonomy cones and exotic nearly Kähler structures on $S^6$ and $S^3\times S^3$, Ann. Math. 185 (2017), 59–130.CrossRefGoogle Scholar
Gibbons, G. W., Page, D. N. and Pope, C. N., Einstein metrics on $S^3,\ \textbf {R}^3$ and $\textbf {R}^4$ bundles, Comm. Math. Phys. 127 (1990), 529–553.CrossRefGoogle Scholar
Hiragane, M., Yasui, Y. and Ishihara, H., Compact Einstein spaces based on quaternionic Kähler manifolds, Classical Quantum Gravity 20 (2003), 3933–3950.CrossRefGoogle Scholar
Jensen, G. R., Einstein metrics on principal fibre bundles, J. Differential Geom. 8 (1973), 599–614.CrossRefGoogle Scholar
Koiso, N., Hypersurfaces of Einstein manifolds, Ann. Sci. Éc. Norm. Supér. (4) 14 (1981), 433–443.CrossRefGoogle Scholar
Koiso, N. and Sakane, Y., Non-homogeneous Kähler–Einstein metrics on compact complex manifolds, in Curvature and Topology of Riemannian Manifolds, Lecture Notes in Mathematics, vol. 1201 (Springer, Berlin, 1986), 165–179.CrossRefGoogle Scholar
Koiso, N. and Sakane, Y., Non-homogeneous Kähler-Einstein metrics on compact complex manifolds. II, Osaka J. Math. 25 (1988), 933–959.Google Scholar
Myers, S. B., Riemannian manifolds with positive mean curvature, Duke Math. J. 8 (1941), 401–404.CrossRefGoogle Scholar
Page, D. N., A compact rotating gravitational instanton, Phys. Lett. B 79 (1978), 235–238.CrossRefGoogle Scholar
Page, D. N. and Pope, C. N., Einstein metrics on quaternionic line bundles, Classical Quantum Gravity 3 (1986), 249–259.CrossRefGoogle Scholar
Page, D. N. and Pope, C. N., Inhomogeneous Einstein metrics on complex line bundles, Classical Quantum Gravity 4 (1987), 213–225.CrossRefGoogle Scholar
Sakane, Y., Examples of compact Einstein Kähler manifolds with positive Ricci tensor, Osaka J. Math. 23 (1986), 585–616.Google Scholar
Wang, J. and Wang, M. Y., Einstein metrics on $S^ 2$-bundles, Math. Ann. 310 (1998), 497–526.CrossRefGoogle Scholar
Wink, M., Cohomogeneity one Ricci solitons from Hopf fibrations, Preprint (2017), arXiv:1706.09712.Google Scholar
Ziller, W., Homogeneous einstein metrics on spheres and projective spaces, Math. Ann. 259 (1982), 351–358.CrossRefGoogle Scholar