Published online by Cambridge University Press: 18 April 2023
Let 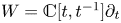 $W = \mathbb {C}[t,t^{-1}]\partial _t$ be the Witt algebra of algebraic vector fields on
$W = \mathbb {C}[t,t^{-1}]\partial _t$ be the Witt algebra of algebraic vector fields on 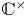 $\mathbb {C}^\times$ and let
$\mathbb {C}^\times$ and let 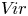 $V\!ir$ be the Virasoro algebra, the unique nontrivial central extension of
$V\!ir$ be the Virasoro algebra, the unique nontrivial central extension of 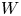 $W$. In this paper, we study the Poisson ideal structure of the symmetric algebras of
$W$. In this paper, we study the Poisson ideal structure of the symmetric algebras of 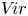 $V\!ir$ and
$V\!ir$ and 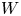 $W$, as well as several related Lie algebras. We classify prime Poisson ideals and Poisson primitive ideals of
$W$, as well as several related Lie algebras. We classify prime Poisson ideals and Poisson primitive ideals of 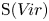 $\operatorname {S}(V\!ir)$ and
$\operatorname {S}(V\!ir)$ and 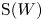 $\operatorname {S}(W)$. In particular, we show that the only functions in
$\operatorname {S}(W)$. In particular, we show that the only functions in 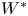 $W^*$ which vanish on a nontrivial Poisson ideal (that is, the only maximal ideals of
$W^*$ which vanish on a nontrivial Poisson ideal (that is, the only maximal ideals of 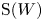 $\operatorname {S}(W)$ with a nontrivial Poisson core) are given by linear combinations of derivatives at a finite set of points; we call such functions local. Given a local function
$\operatorname {S}(W)$ with a nontrivial Poisson core) are given by linear combinations of derivatives at a finite set of points; we call such functions local. Given a local function 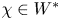 $\chi \in W^*$, we construct the associated Poisson primitive ideal through computing the algebraic symplectic leaf of
$\chi \in W^*$, we construct the associated Poisson primitive ideal through computing the algebraic symplectic leaf of 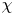 $\chi$, which gives a notion of coadjoint orbit in our setting. As an application, we prove a structure theorem for subalgebras of
$\chi$, which gives a notion of coadjoint orbit in our setting. As an application, we prove a structure theorem for subalgebras of 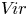 $V\!ir$ of finite codimension and show, in particular, that any such subalgebra of
$V\!ir$ of finite codimension and show, in particular, that any such subalgebra of 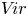 $V\!ir$ contains the central element
$V\!ir$ contains the central element 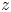 $z$, substantially generalising a result of Ondrus and Wiesner on subalgebras of codimension one. As a consequence, we deduce that
$z$, substantially generalising a result of Ondrus and Wiesner on subalgebras of codimension one. As a consequence, we deduce that 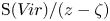 $\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple if and only if
$\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple if and only if 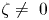 $\zeta \neq ~0$.
$\zeta \neq ~0$.