Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T23:18:58.009Z Has data issue: false hasContentIssue false
  • English
  • Français

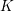Picard groups of higher real $K$-theory spectra at height 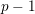$p-1$

Part of: Cycles and subschemes Operations and obstructions Homotopy theory Homotopy groups

Published online by Cambridge University Press:  20 June 2017

Drew Heard ,
Akhil Mathew  and
Vesna Stojanoska
Drew Heard
Affiliation:
Department of Mathematics, Universität Hamburg, D-20146 Hamburg, Germany email [email protected]
Akhil Mathew
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA email [email protected]
Vesna Stojanoska
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

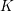Using the descent spectral sequence for a Galois extension of ring spectra, we compute the Picard group of the higher real $K$-theory spectra of Hopkins and Miller at height 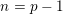$n=p-1$, for 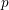$p$ an odd prime. More generally, we determine the Picard groups of the homotopy fixed points spectra 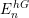$E_{n}^{hG}$, where 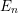$E_{n}$ is Lubin–Tate 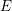$E$-theory at the prime 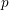$p$ and height 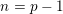$n=p-1$, and 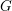$G$ is any finite subgroup of the extended Morava stabilizer group. We find that these Picard groups are always cyclic, generated by the suspension.

Keywords

Picard groupshigher real K-theoriesGalois descentpower operations

MSC classification

Primary: 14C22: Picard groups 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.) 55Q51: $v_n$-periodicity 55S99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 9 , September 2017 , pp. 1820 - 1854
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almkvist, G. and Fossum, R., Decomposition of exterior and symmetric powers of indecomposable Z/p Z -modules in characteristic p and relations to invariants , in Séminaire d’Algèbre Paul Dubreil, 30ème année (Paris 1976–1977), Lecture Notes in Mathematics, vol. 641 (Springer, Berlin, 1978), 1–111; MR 499459 (81b:14024).Google Scholar
Ando, M., Blumberg, A. J., Gepner, D., Hopkins, M. J. and Rezk, C., Units of ring spectra, orientations and Thom spectra via rigid infinite loop space theory , J. Topol. 7 (2014), 1077–1117; MR 3286898.Google Scholar
Baker, A. and Richter, B., Invertible modules for commutative S-algebras with residue fields , Manuscripta Math. 118 (2005), 99–119; MR 2171294 (2006f:55009).CrossRefGoogle Scholar
Baker, A. and Richter, B., Realizability of algebraic Galois extensions by strictly commutative ring spectra , Trans. Amer. Math. Soc. 359 (2007), 827–857 (electronic); MR 2255198 (2007m:55007).Google Scholar
Beaudry, A., The algebraic duality resolution at p = 2 , Algebr. Geom. Topol. 15 (2015), 3653–3705; MR 3450774.Google Scholar
Behrens, M., The homotopy groups of S E (2) at p⩾5 revisited , Adv. Math. 230 (2012), 458–492; MR 2914955.Google Scholar
Bobkova, I., Resolutions in the $K(2)$ -local category at the prime 2, PhD thesis, Northwestern University (ProQuest LLC, Ann Arbor, MI 2014); MR 3251316.Google Scholar
Bujard, C., Finite subgroups of extended Morava stabilizer groups, Preprint (2012), arXiv:1206.1951.Google Scholar
Cohen, F. R., Lada, T. J. and May, J. P., The homology of iterated loop spaces, Lecture Notes in Mathematics, vol. 533 (Springer, New York, 1976); MR 0436146 (55 #9096).CrossRefGoogle Scholar
Devinatz, E. S. and Hopkins, M. J., The action of the Morava stabilizer group on the Lubin–Tate moduli space of lifts , Amer. J. Math. 117 (1995), 669–710; MR 1333942 (97a:55007).Google Scholar
Devinatz, E. S. and Hopkins, M. J., Homotopy fixed point spectra for closed subgroups of the Morava stabilizer groups , Topology 43 (2004), 1–47; MR 2030586 (2004i:55012).CrossRefGoogle Scholar
Fröhlich, A., Formal groups, Lecture Notes in Mathematics, vol. 74 (Springer, Berlin, 1968); MR 0242837 (39 #4164).Google Scholar
Gepner, D. and Lawson, T., Brauer groups and Galois cohomology of commutative ring spectra, Preprint (2016), arXiv:1607.01118.Google Scholar
Goerss, P., Henn, H.-W. and Mahowald, M., The homotopy of L 2 V (1) for the prime 3 , in Categorical decomposition techniques in algebraic topology (Isle of Skye 2001), Progress in Mathematics, vol. 215 (Birkhäuser, Basel, 2004), 125–151; MR 2039763 (2004k:55010).Google Scholar
Goerss, P., Henn, H.-W., Mahowald, M. and Rezk, C., A resolution of the K (2)-local sphere at the prime 3 , Ann. of Math. (2) 162 (2005), 777–822; MR 2183282 (2006j:55016).Google Scholar
Goerss, P., Henn, H.-W., Mahowald, M. and Rezk, C., On Hopkins’ Picard groups for the prime 3 and chromatic level 2 , J. Topol. 8 (2015), 267–294; MR 3335255.CrossRefGoogle Scholar
Goerss, P. G. and Hopkins, M. J., Moduli spaces of commutative ring spectra , in Structured ring spectra, London Mathematical Society Lecture Note Series, vol. 315 (Cambridge University Press, Cambridge, 2004), 151–200; MR 2125040 (2006b:55010).Google Scholar
Gorbounov, V., Mahowald, M. and Symonds, P., Infinite subgroups of the Morava stabilizer groups , Topology 37 (1998), 1371–1379; MR 1632952 (99m:16032).CrossRefGoogle Scholar
Heard, D., The Tate spectrum of the higher real $K$ -theories at height $n=p-1$ , Preprint (2015), arXiv:1501.07759.Google Scholar
Henn, H.-W., On finite resolutions of K (n)-local spheres , in Elliptic cohomology, London Mathematical Society Lecture Note Series, vol. 342 (Cambridge University Press, Cambridge, 2007), 122–169; MR 2330511 (2009e:55014).Google Scholar
Hewett, T., Finite subgroups of division algebras over local fields , J. Algebra 173 (1995), 518–548; MR 1327867 (96b:16012).CrossRefGoogle Scholar
Hill, M., Computational methods for higher real $K$ -theory with applications to TMF, PhD thesis, Massachusetts Institute of Technology (2006).Google Scholar
Hill, M. and Meier, L., The $C_{2}$ -spectrum $Tmf_{1}(3)$ and its invertible modules, Algebr. Geom. Topol., to appear, arXiv:1507.08115.Google Scholar
Hopkins, M. J., Mahowald, M. and Sadofsky, H., Constructions of elements in Picard groups , in Topology and representation theory (Evanston, IL 1992), Contemporary Mathematic, vol. 158 (American Mathematical Society, Providence, RI, 1994), 89–126; MR 1263713 (95a:55020).CrossRefGoogle Scholar
Karamanov, N., On Hopkins’ Picard group Pic2 at the prime 3 , Algebr. Geom. Topol. 10 (2010), 275–292; MR 2602836 (2011c:55013).Google Scholar
Kraines, D., Massey higher products , Trans. Amer. Math. Soc. 124 (1966), 431–449; MR 0202136 (34 #2010).Google Scholar
Lader, O., Une résolution projective pour le second groupe de Morava pour $p\geqslant 5$ et applications, PhD thesis, Institut de Recherche Mathmatiques Avance (July 2013).Google Scholar
Lurie, J., Derived algebraic geometry XI: descent theorems, available at http://www.math.harvard.edu/∼lurie/papers/DAG-XI.pdf.Google Scholar
Mathew, A., A thick subcategory theorem for modules over certain ring spectra , Geom. Topol. 19 (2015), 2359–2392; MR 3375530.Google Scholar
Mathew, A., The Galois group of a stable homotopy theory , Adv. Math. 291 (2016), 403–541; MR 3459022.CrossRefGoogle Scholar
Mathew, A. and Meier, L., Affineness and chromatic homotopy theory , J. Topol. 8 (2015), 476–528; MR 3356769.Google Scholar
Mathew, A., Naumann, N. and Noel, J., Derived induction and restriction theory, Preprint (2015), arXiv:1507.06867.Google Scholar
Mathew, A. and Stojanoska, V., The Picard group of topological modular forms via descent theory , Geom. Topol. 20 (2016), 3133–3217.CrossRefGoogle Scholar
Mumford, D., Lectures on curves on an algebraic surface, With a section by G. M. Bergman, Annals of Mathematics Studies, vol. 59 (Princeton University Press, Princeton, NJ, 1966); MR 0209285 (35 #187).Google Scholar
Nave, L. S., The cohomology of finite subgroups of Morava stabilizer groups and Smith–Toda complexes, PhD thesis, University of Washington (ProQuest LLC, Ann Arbor, MI 1999); MR 2699376.Google Scholar
Nave, L. S., The Smith–Toda complex V ((p + 1)/2) does not exist , Ann. of Math. (2) 171 (2010), 491–509; MR 2630045 (2011m:55012).CrossRefGoogle Scholar
Priddy, S., Mod-p right derived functor algebras of the symmetric algebra functor , J. Pure Appl. Algebra 3 (1973), 337–356; MR 0342592 (49 #7338).Google Scholar
Ravenel, D. C., The non-existence of odd primary Arf invariant elements in stable homotopy , Math. Proc. Cambridge Philos. Soc. 83 (1978), 429–443; MR 0474291 (57 #13938).CrossRefGoogle Scholar
Rezk, C., Notes on the Hopkins–Miller theorem , in Homotopy theory via algebraic geometry and group representations (Evanston, IL 1997), Contemporary Mathematic, vol. 220 (American Mathematical Society, Providence, RI, 1998), 313–366; MR 1642902 (2000i:55023).Google Scholar
Rognes, J., Galois extensions of structured ring spectra. Stably dualizable groups , Mem. Amer. Math. Soc. 192 (2008), viii + 137; MR 2387923 (2009c:55007).Google Scholar
Serre, J.-P., Local fields, Graduate Texts in Mathematics, vol. 67 (Springer, New York, 1979). Translated from the French by Marvin Jay Greenberg; MR 554237 (82e:12016).Google Scholar
Grothendieck, A. and Raynaud, M., Revêtements étales et groupe fondamental (SGA 1) , in Séminaire de géométrie algébrique du Bois Marie 1960–61, Documents Mathématiques (Paris), vol. 3 (Société Mathématique de France, Paris, 2003), updated and annotated reprint of the 1971 original; MR 2017446 (2004g:14017).Google Scholar
Toda, H., An important relation in homotopy groups of spheres , Proc. Japan Acad. 43 (1967), 839–842; MR 0230310 (37 #5872).Google Scholar
Toda, H., Extended pth powers of complexes and applications to homotopy theory , Proc. Japan Acad. 44 (1968), 198–203; MR 0230311 (37 #5873).Google Scholar