Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-02T04:41:26.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect points of abelian varieties

Part of: Field extensions Abelian varieties and schemes (Co)homology theory

Published online by Cambridge University Press:  08 September 2023

Emiliano Ambrosi Open the ORCID record for Emiliano Ambrosi [Opens in a new window]
Emiliano Ambrosi*
Affiliation:
Université de Strasbourg, 7 rue René Descartes, 67084 Strasbourg, France [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 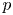$p$ be a prime number, 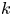$k$ a finite field of characteristic 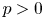$p>0$ and 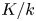$K/k$ a finitely generated extension of fields. Let 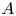$A$ be a 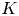$K$-abelian variety such that all the isogeny factors are neither isotrivial nor of 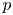$p$-rank zero. We give a necessary and sufficient condition for the finite generation of 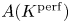$A(K^{\mathrm {perf}})$ in terms of the action of 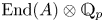$\mathrm {End}(A)\otimes \mathbb {Q}_p$ on the 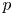$p$-divisible group 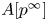$A[p^{\infty }]$ of 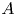$A$. In particular, we prove that if 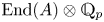$\mathrm {End}(A)\otimes \mathbb {Q}_p$ is a division algebra, then 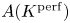$A(K^{\mathrm {perf}})$ is finitely generated. This implies the ‘full’ Mordell–Lang conjecture for these abelian varieties. In addition, we prove that all the infinitely 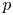$p$-divisible elements in 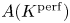$A(K^{\mathrm {perf}})$ are torsion. These reprove and extend previous results to the non-ordinary case.

Keywords

Abelian varietiesinseparable extensionsrational pointsp-adic cohomologies

MSC classification

Primary: 14K15: Arithmetic ground fields 14F30: $p$-adic cohomology, crystalline cohomology 12F15: Inseparable extensions
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 11 , November 2023 , pp. 2261 - 2278
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author would like to thank A. Cadoret, B. Kahn, C. Gasbarri and A. Shiho for useful discussions and G. Ancona for many suggestions on how to improve the exposition. The author is grateful to an anonymous referee whose suggestions helped to improve the exposition and the clarity of the paper and for pointing out the work of Trihan which greatly simplified the proof of Proposition 4.1.2. Part of this work has been done when the author was a guest of the Max Planck Institute for Mathematics (MPIM) in Bonn and he would like to express his gratitude to the MPIM for their hospitality and financial support.

References

Ambrosi, E. and D'Addezio, M., Maximal tori of monodromy groups of $F$-isocrystals and an application to abelian varieties, Algebr. Geom. 9 (2022), 633–650.10.14231/AG-2022-019CrossRefGoogle Scholar
Andreatta, F. and Barbieri-Viale, L., Crystalline realizations of 1-motives, Math. Ann. 331 (2005), 111–172.10.1007/s00208-004-0576-4CrossRefGoogle Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres (première partie), Preprint (1996).Google Scholar
Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné cristalline II, Lecture Notes in Mathematics, vol. 930 (Springer, 1982).10.1007/BFb0093025CrossRefGoogle Scholar
Bosch, S., Lutkebohmert, W. and Raynaud, M., Néron Models, A Series of Modern Surveys in Mathematics, vol. 21 (Springer, 1990).10.1007/978-3-642-51438-8CrossRefGoogle Scholar
Bragg, D. and Lieblich, M., Perfect points on genus one curves and consequences for supersingular K3 surfaces, Compos. Math. 158 (2022), 1052–1083.10.1112/S0010437X22007382CrossRefGoogle Scholar
Česnavic〶ius, K., Poitou–Tate without restrictions on the order, Math. Res. Lett. 22 (2015), 1621–1666.10.4310/MRL.2015.v22.n6.a5CrossRefGoogle Scholar
D'Addezio, M., Parabolicity conjecture of $F$-isocrystals, Ann. of Math. (2023), to appear.Google Scholar
de Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96.10.1007/BF02698637CrossRefGoogle Scholar
de Jong, A. J., Homomorphisms of Barsotti–Tate groups and crystals in positive characteristic, Invent. Math. 134 (1998), 301–333.10.1007/s002220050266CrossRefGoogle Scholar
Deligne, P. and Katz, N., Groupes de monodromie en géométrie algébrique II, Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969 (SGA 7 II), Lecture Notes in Mathematics, vol. 340 (Springer, 1973).Google Scholar
Dixon, J. D., du Sautoy, M. P. F., Mann, A. and Segal, D., Analytic pro-p groups, London Mathematical Society Lecture Note Series, vol. 157 (Cambridge University Press, 1991).Google Scholar
Étesse, J. Y., Descente étale des $F$-isocristaux surconvergents et rationalité des fonctions $L$ de schémas abéliens, Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 575–603.10.1016/S0012-9593(02)01099-6CrossRefGoogle Scholar
Faltings, G., Diophantine approximation on abelian varieties, Ann. of Math. 133 (1991), 549–576.10.2307/2944319CrossRefGoogle Scholar
Ghioca, D., Elliptic curves over the perfect closure of a function field, Canad. Math. Bull. 53 (2010), 87–94.10.4153/CMB-2010-019-9CrossRefGoogle Scholar
Ghioca, D. and Moosa, R., Division points on subvarieties of isotrivial semi-abelian varieties, Int. Math. Res. Not. IMRN 2006 (2006), 1–23.Google Scholar
Grub, T., Kedlaya, K. and Upton, J., A cut-by-curves criterion for overconvergent of F-isocrystals, Preprint (2021).Google Scholar
Helm, D., An ordinary abelian variety with an étale self-isogeny of $p$-power degree and no isotrivial factors, Math. Res. Lett. 20 (2022), 445–454.10.4310/MRL.2022.v29.n2.a6CrossRefGoogle Scholar
Hindry, M., Autour d'une conjecture de Serge Lang, Invent. Math. 94 (1988), 575–603.10.1007/BF01394276CrossRefGoogle Scholar
Hrushovski, E., The Mordell–Lang conjecture for function fields, J. Amer. Math. Soc. 9 (1996), 667–690.10.1090/S0894-0347-96-00202-0CrossRefGoogle Scholar
Jannsen, U., Motivic sheaves and filtrations on Chow groups, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55 (American Mathematical Society, 1994), 245–302.10.1090/pspum/055.1/1265533CrossRefGoogle Scholar
Kedlaya, K. S., Full faithfulness for overconvergent F-isocrystals, in Geometric Aspects of Dwork Theory, vol. II (De Gruyter, 2004), 819–883.10.1515/9783110198133.2.819CrossRefGoogle Scholar
Kedlaya, K. S., Notes on isocrystals, J. Number Theory 237 (2022), 353–394.10.1016/j.jnt.2021.12.004CrossRefGoogle Scholar
Lang, S. and Néron, A., Rational points of abelian varieties over function fields, Amer. J. Math. 81 (1959), 95–118.10.2307/2372851CrossRefGoogle Scholar
Messing, W., The crystals associated to Barsotti–Tate groups: with applications to abelian schemes, Lecture Notes in Mathematics, vol. 264 (Springer, 1972).10.1007/BFb0058301CrossRefGoogle Scholar
Morrow, M., A variational Tate conjecture in crystalline cohomology, J. Eur. Math. Soc. 21 (2019), 3467–3511.10.4171/JEMS/907CrossRefGoogle Scholar
Pál, A., The $p$-adic monodromy group of abelian varieties over global function fields of characteristic p, Doc. Math. 27 (2022), 1509–1579.10.4171/dm/903CrossRefGoogle Scholar
Rössler, D., On the group of purely inseparable points of an abelian variety defined over a function field of positive characteristic I, Comment. Math. Helv. 90 (2015), 23–52.10.4171/CMH/344CrossRefGoogle Scholar
Rössler, D., On the group of purely inseparable points of an abelian variety defined over a function field of positive characteristic II, Algebra Number Theory 14 (2020), 1123–1173.CrossRefGoogle Scholar
Serre, J. P., Sur les groupes de congruence des variétés abéliennes, Izv. Akad. Nauk SSSR Ser. Mat. 28 (1964), 3–20.Google Scholar
The Stacks project authors, The stacks project (2020), https://stacks.math.columbia.edu.Google Scholar
Tate, J., Endomorphisms of abelian varieties over finite fields, Invent. Math. 2 (1966), 134–144.10.1007/BF01404549CrossRefGoogle Scholar
Trihan, F., A note on semistable Barsotti-Tate groups, J. Math. Sci. Univ. Tokyo 15 (2008), 411–425.Google Scholar
Tsuzuki, N., Minimal slope conjecture of $F$-isocrystals, Invent. Math. 231 (2023), 39–109.CrossRefGoogle Scholar
Xinyi, Y., Positivity of Hodge bundles of abelian varieties over some function fields, Compos. Math. 157 (2021), 1964–2000.Google Scholar