Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Kefeng
Wan, Xueyuan
and
Yang, Xiaokui
2019.
Logarithmic vanishing theorems for effective q-ample divisors.
Science China Mathematics,
Vol. 62,
Issue. 11,
p.
2331.
Yang, Xiaokui
2020.
RC-positive metrics on rationally connected manifolds.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Yang, Xiaokui
2021.
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 3,
p.
1023.
Liu, Jie
Ou, Wenhao
and
Yang, Xiaokui
2021.
Strictly nef vector bundles and characterizations of ℙ
n
.
Complex Manifolds,
Vol. 8,
Issue. 1,
p.
148.
Ohsawa, Takeo
and
Pawlaschyk, Thomas
2022.
Analytic Continuation and q-Convexity.
p.
37.
Matsumura, Shin-ichi
2022.
Open problems on structure of positively curved projective varieties.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 31,
Issue. 3,
p.
1011.
Wang, Jun
and
Yang, Xiaokui
2022.
RC-positivity and scalar-flat metrics on ruled surfaces.
Mathematische Zeitschrift,
Vol. 301,
Issue. 1,
p.
917.
Höring, Andreas
and
Peternell, Thomas
2024.
Stein complements in compact Kähler manifolds.
Mathematische Annalen,
Vol. 390,
Issue. 2,
p.
2075.
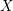 $X$ be a smooth projective manifold with
$X$ be a smooth projective manifold with 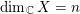 $\dim _{\mathbb{C}}X=n$. We show that if a line bundle
$\dim _{\mathbb{C}}X=n$. We show that if a line bundle 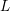 $L$ is
$L$ is 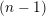 $(n-1)$-ample, then it is
$(n-1)$-ample, then it is 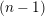 $(n-1)$-positive. This is a partial converse to the Andreotti–Grauert theorem. As an application, we show that a projective manifold
$(n-1)$-positive. This is a partial converse to the Andreotti–Grauert theorem. As an application, we show that a projective manifold 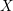 $X$ is uniruled if and only if there exists a Hermitian metric
$X$ is uniruled if and only if there exists a Hermitian metric 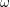 $\unicode[STIX]{x1D714}$ on
$\unicode[STIX]{x1D714}$ on 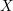 $X$ such that its Ricci curvature
$X$ such that its Ricci curvature 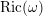 $\text{Ric}(\unicode[STIX]{x1D714})$ has at least one positive eigenvalue everywhere.
$\text{Ric}(\unicode[STIX]{x1D714})$ has at least one positive eigenvalue everywhere.