Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Breuil, Christophe
Hellmann, Eugen
and
Schraen, Benjamin
2017.
Smoothness and classicality on Eigenvarieties.
Inventiones mathematicae,
Vol. 209,
Issue. 1,
p.
197.
Ding, Yiwen
2019.
Some Results on the Locally Analytic Socle for $\textrm{GL}_{n}(\mathbb {Q}_{p})$.
International Mathematics Research Notices,
Vol. 2019,
Issue. 19,
p.
5989.
Breuil, Christophe
Hellmann, Eugen
and
Schraen, Benjamin
2019.
A local model for the trianguline variety and applications.
Publications mathématiques de l'IHÉS,
Vol. 130,
Issue. 1,
p.
299.
Ding, Yiwen
2019.
Companion points and locally analytic socle for GL2(L).
Israel Journal of Mathematics,
Vol. 231,
Issue. 1,
p.
47.
Bergdall, John
2020.
Smoothness of definite unitary eigenvarieties at critical points.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 759,
p.
29.
Berger, Laurent
and
Di Matteo, Giovanni
2021.
On triangulable tensor products of B-pairs and trianguline representations.
International Journal of Number Theory,
Vol. 17,
Issue. 10,
p.
2221.
Newton, James
and
Thorne, Jack A.
2021.
Symmetric power functoriality for holomorphic modular forms.
Publications mathématiques de l'IHÉS,
Vol. 134,
Issue. 1,
p.
1.
Bergdall, John
and
Hansen, David
2024.
On 𝑝-adic 𝐿-functions for Hilbert modular forms.
Memoirs of the American Mathematical Society,
Vol. 298,
Issue. 1489,
Breuil, Christophe
and
Ding, Yiwen
2024.
Bernstein Eigenvarieties.
Peking Mathematical Journal,
Vol. 7,
Issue. 2,
p.
471.
Johansson, Christian
and
Ludwig, Judith
2024.
Endoscopy on SL2-eigenvarieties.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
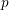 $p$-adic families of
$p$-adic families of 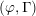 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules $p$-adic variation of triangulations over
$p$-adic variation of triangulations over  $p$-adic families of
$p$-adic families of 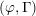 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules. In particular, we study certain canonical sub-filtrations of the pointwise triangulations and show that they extend to affinoid neighborhoods of crystalline points. This generalizes results of Kedlaya, Pottharst and Xiao and (independently) Liu in the case where one expects the entire triangulation to extend. We also study the ramification of weight parameters over natural
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules. In particular, we study certain canonical sub-filtrations of the pointwise triangulations and show that they extend to affinoid neighborhoods of crystalline points. This generalizes results of Kedlaya, Pottharst and Xiao and (independently) Liu in the case where one expects the entire triangulation to extend. We also study the ramification of weight parameters over natural 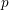 $p$-adic families.
$p$-adic families.