Article contents
The 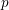 $p$-adic Gross–Zagier formula on Shimura curves
$p$-adic Gross–Zagier formula on Shimura curves
Published online by Cambridge University Press: 11 July 2017
Abstract
We prove a general formula for the 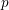 $p$-adic heights of Heegner points on modular abelian varieties with potentially ordinary (good or semistable) reduction at the primes above
$p$-adic heights of Heegner points on modular abelian varieties with potentially ordinary (good or semistable) reduction at the primes above 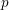 $p$. The formula is in terms of the cyclotomic derivative of a Rankin–Selberg
$p$. The formula is in terms of the cyclotomic derivative of a Rankin–Selberg 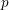 $p$-adic
$p$-adic 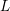 $L$-function, which we construct. It generalises previous work of Perrin-Riou, Howard, and the author to the context of the work of Yuan–Zhang–Zhang on the archimedean Gross–Zagier formula and of Waldspurger on toric periods. We further construct analytic functions interpolating Heegner points in the anticyclotomic variables, and obtain a version of our formula for them. It is complemented, when the relevant root number is
$L$-function, which we construct. It generalises previous work of Perrin-Riou, Howard, and the author to the context of the work of Yuan–Zhang–Zhang on the archimedean Gross–Zagier formula and of Waldspurger on toric periods. We further construct analytic functions interpolating Heegner points in the anticyclotomic variables, and obtain a version of our formula for them. It is complemented, when the relevant root number is 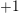 $+1$ rather than
$+1$ rather than 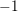 $-1$, by an anticyclotomic version of the Waldspurger formula. When combined with work of Fouquet, the anticyclotomic Gross–Zagier formula implies one divisibility in a
$-1$, by an anticyclotomic version of the Waldspurger formula. When combined with work of Fouquet, the anticyclotomic Gross–Zagier formula implies one divisibility in a 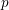 $p$-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. Other applications described in the text will appear separately.
$p$-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. Other applications described in the text will appear separately.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 12
- Cited by


