Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T01:09:45.323Z Has data issue: false hasContentIssue false
  • English
  • Français

On the volume of isolated singularities

Part of: Computational aspects in algebraic geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  23 June 2014

Yuchen Zhang
Yuchen Zhang*
Affiliation:
Department of Mathematics, University of Utah, 155 S 1400 E Room 233, Salt Lake City, UT 84102, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give an equivalent definition of the local volume of an isolated singularity 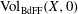$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\rm Vol}_{\text {BdFF}}(X,0)$ given in [S. Boucksom, T. de Fernex, C. Favre, The volume of an isolated singularity. Duke Math. J. 161 (2012), 1455–1520] in the 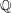$\mathbb{Q}$-Gorenstein case and we generalize it to the non-$\mathbb{Q}$-Gorenstein case. We prove that there is a positive lower bound depending only on the dimension for the non-zero local volume of an isolated singularity if 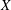$X$ is Gorenstein. We also give a non-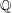$\mathbb{Q}$-Gorenstein example with 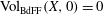${\rm Vol}_{\text {BdFF}}(X,0)=0$, which does not allow a boundary 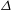$\Delta $ such that the pair 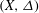$(X,\Delta )$ is log canonical.

Keywords

isolated singularitiesnon-ℚ-Gorensteinnef envelopelog canonical modification

MSC classification

Secondary: 14J17: Singularities 14Q15: Higher-dimensional varieties
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 8 , August 2014 , pp. 1413 - 1424
Copyright
© The Author 2014 

References

Boucksom, S., de Fernex, T. and Favre, C., The volume of an isolated singularity, Duke Math. J. 161 (2012), 1455–1520.CrossRefGoogle Scholar
Broustet, A. and Höring, A., Singularities of varieties admitting an endomorphism, Preprint (2012), arXiv:1210.6254.Google Scholar
de Fernex, T. and Hacon, C., Singularites on normal varieties, Compositio. Math. 145 (2009), 393–414.Google Scholar
Fulger, M., Local volumes, PhD thesis, University of Michigan (2012).Google Scholar
Hacon, C., McKernan, J. and Xu, C., ACC for log canonical thresholds, Preprint (2012),arXiv:1208.4150.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998).Google Scholar
Kollár, J. et al. , Flips and abundance for algebraic threefolds. Papers from the Second Summer Seminar on Algebraic Geometry held at University of Utah, Salt Lake City, Utah, August 1991, Astérisque 211 (Société Mathématique de France, Paris, 1992).Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry I, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series], vol. 48 (Springer, Berlin, 2004).Google Scholar
Odaka, F. and Xu, C., Log-canonical models of singular pairs and its applications, Math. Res. Lett. 19 (2012), 325–334.Google Scholar
Shokurov, V., Complements on surfaces, J. Math. Sci. (N. Y.) 102 (2000), 3876–3932.Google Scholar
Urbinati, S., Discrepancies of non-ℚ-Gorenstein varieties, Michigan Math. J. 61 (2012), 265–277.Google Scholar