Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-04T21:21:05.542Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Iwasawa theory of the Lubin–Tate moduli space

Part of: Locally compact groups and their algebras Algebraic number theory: local and $p$-adic fields Algebraic groups

Published online by Cambridge University Press:  26 February 2013

Jan Kohlhaase
Jan Kohlhaase*
Affiliation:
Mathematisches Institut, Westfälische Wilhelms-Universität Münster, Einsteinstraße 62, D-48149 Münster, Germany (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

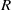We study the affine formal algebra $R$ of the Lubin–Tate deformation space as a module over two different rings. One is the completed group ring of the automorphism group 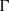$\Gamma $ of the formal module of the deformation problem, the other one is the spherical Hecke algebra of a general linear group. In the most basic case of height two and ground field 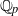$\mathbb {Q}_p$, our structure results include a flatness assertion for 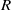$R$ over the spherical Hecke algebra and allow us to compute the continuous (co)homology of 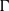$\Gamma $ with coefficients in 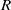$R$.

Keywords

moduli spacesformal groups$p$-adic representation theory

MSC classification

Secondary: 14L05: Formal groups, $p$-divisible groups 22D10: Unitary representations of locally compact groups 11S23: Integral representations
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 5 , May 2013 , pp. 793 - 839
Copyright
Copyright © 2013 The Author(s) 

References

[Beh12]Behrens, M., The homotopy groups of the $E(2)$-local sphere at $p \gt 3$, revisited, Adv. Math. 230 (2012), 458–492.Google Scholar
[Bor91]Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).Google Scholar
[Bos08]Bosch, S., Lectures on formal and rigid geometry, Preprint (2008), available atwww.math.uni-muenster.de/sfb/about/publ/heft378.pdf.Google Scholar
[Bou06]Bourbaki, N., Algèbre commutative (Springer, Berlin, 2006).CrossRefGoogle Scholar
[Bru66]Brumer, A., Pseudocompact algebras, profinite groups and class formations, J. Algebra 4 (1966), 442–470.CrossRefGoogle Scholar
[Cha96]Chai, C.-L., The group action on the closed fiber of the Lubin–Tate moduli space, Duke Math. J. 82 (1996), 725–754.Google Scholar
[deJ95]de Jong, J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Inst. Hautes Études Sci. 82 (1995), 5–96.Google Scholar
[DH95]Devinatz, E. S. and Hopkins, M. J., The action of the Morava stabilizer group on the Lubin–Tate moduli space of lifts, Amer. J. Math. 117 (1995), 669–710.Google Scholar
[Dri74]Drinfeld, V. G., Elliptic modules, Math. USSR Sbornik 23 (1974), 561–592.CrossRefGoogle Scholar
[FGL08]Fargues, L., Genestier, A. and Lafforgue, V., L’isomorphisme entre les tours de Lubin–Tate et de Drinfeld, Progress in Mathematics, vol. 262 (Birkhäuser, Boston, MA, 2008).Google Scholar
[Gro11]Große-Klönne, E., On the universal module of -adic spherical Hecke algebras, Preprint (2011), available at http://www.math.hu-berlin.de/∼zyska/Grosse-Kloenne/Preprints.html.Google Scholar
[GH94]Gross, B. H. and Hopkins, M. J., Equivariant vector bundles on the Lubin–Tate moduli space, Contemp. Math. 158 (1994), 23–88.Google Scholar
[Gru79]Grünenfelder, L., On the homology of filtered and graded rings, J. Pure Appl. Algebra 14 (1979), 21–37.CrossRefGoogle Scholar
[Haz78]Hazewinkel, M., Formal groups and applications, Pure and Applied Mathematics, vol. 78 (Academic Press, New York, 1978).Google Scholar
[Hov93]Hovey, M., Bousfield localization functors and Hopkins’ chromatic splitting conjecture, in The Čech centennial (Boston, MA, 1993), Contemporary Mathematics, vol. 181 (American Mathematical Society, Providence, RI, 1993), 225–250.Google Scholar
[HvO96]Huishi, L. and van Oystaeyen, F., Zariskian filtrations, -Monographs in Mathematics, vol. 2 (Kluwer, 1996).Google Scholar
[Kna88]Knapp, A., Lie groups, lie algebras, and cohomology, Mathematical Notes, vol. 34 (Princeton, 1988).Google Scholar
[Koh12]Kohlhaase, J., Iwasawa modules arising from deformation spaces of -divisible formal group laws, Preprint (2012), available at http://www.math.uni-muenster.de/u/kohlhaaj/publ.html.Google Scholar
[Koh11]Kohlhaase, J., The cohomology of locally analytic representations, J. Reine Angew. Math. (Crelle) 651 (2011), 187–240.Google Scholar
[KS12]Kohlhaase, J. and Schraen, B., Homological vanishing theorems for locally analytic representations, Math. Ann. 353 (2012), 219–258.CrossRefGoogle Scholar
[Laz65]Lazard, M., Groupes analytiques -adiques, Publ. Inst. Hautes Études Sci. 26 (1965), 5–219.Google Scholar
[NSW00]Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, Grundlehren der Mathematischen Wissenschaften, vol. 323 (Springer, New York, 2000).Google Scholar
[OS10]Orlik, S. and Strauch, M., On Jordan–Hölder series of some locally analytic representations, Preprint (2010); arXiv:1001.0323.Google Scholar
[PR94]Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, New York, 1994).Google Scholar
[RZ96]Rapoport, M. and Zink, Th., Period spaces for -divisible groups, Annals of Mathematics Studies, vol. 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
[Sch11]Schneider, P., -adic Lie groups, Grundlehren der Mathematischen Wissenschaften, vol. 344 (Springer, 2011).Google Scholar
[ST02a]Schneider, P. and Teitelbaum, J., Locally analytic distributions and $p$-adic representation theory, with applications to $\mathrm {GL}_2$, J. Amer. Math. Soc. 15 (2002), 443–468.Google Scholar
[ST02b]Schneider, P. and Teitelbaum, J., Banach space representations and Iwasawa theory, Israel J. Math. 127 (2002), 359–380.Google Scholar
[SY95]Shimomura, K. and Yabe, A., The homotopy groups $\pi _*(L_2S^0)$, Topology 34 (1995), 261–289.Google Scholar
[Str08]Strauch, M., Deformation spaces of one-dimensional formal groups and their cohomology, Adv. Math. 217 (2008), 889–951.CrossRefGoogle Scholar
[Stu00]Stumbo, F., Minimal length coset representatives for quotients of parabolic subgroups in Coxeter groups, Boll. Unione Mat. Ital. 8 (2000), 699–715.Google Scholar
[Sym04]Symonds, P., The Tate–Farrell Cohomology of the Morava stabilizer group $S_{p-1}$ with coefficients in $E_{p-1}$, Contemp. Math. 346 (2004), 485–492.Google Scholar
[SW00]Symonds, P. and Weigel, T., Cohomology of $p$-adic analytic groups, in New horizons in pro- groups, Progress in Mathematics, vol. 184, eds du Sautoy, M., Segal, D. and Shalev, A. (Birkhäuser, 2000), 349–410.Google Scholar
[Wil98]Wilson, J. S., Profinite groups, London Mathematical Society Monographs, vol. 19 (Oxford, 1998).Google Scholar
[Yu95]Yu, J.-K., On the moduli of quasi-canonical liftings, Compositio Math. 96 (1995), 293–321.Google Scholar