No CrossRef data available.
Published online by Cambridge University Press: 16 September 2024
The deepest arithmetic invariants attached to an algebraic variety defined over a number field 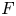 $F$ are conjecturally captured by the integral part of its motivic cohomology. There are essentially two ways of defining it when
$F$ are conjecturally captured by the integral part of its motivic cohomology. There are essentially two ways of defining it when 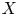 $X$ is a smooth projective variety: one is via the
$X$ is a smooth projective variety: one is via the 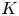 $K$-theory of a regular integral model, the other is through its
$K$-theory of a regular integral model, the other is through its 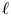 $\ell$-adic realization. Both approaches are conjectured to coincide. This paper initiates the study of motivic cohomology for global fields of positive characteristic, hereafter named
$\ell$-adic realization. Both approaches are conjectured to coincide. This paper initiates the study of motivic cohomology for global fields of positive characteristic, hereafter named 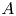 $A$-motivic cohomology, where classical mixed motives are replaced by mixed Anderson
$A$-motivic cohomology, where classical mixed motives are replaced by mixed Anderson  $A$-motives. Our main objective is to set the definitions of the integral part and the good
$A$-motives. Our main objective is to set the definitions of the integral part and the good 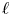 $\ell$-adic part of the
$\ell$-adic part of the 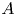 $A$-motivic cohomology using Gardeyn's notion of maximal models as the analogue of regular integral models of varieties. Our main result states that the integral part is contained in the good
$A$-motivic cohomology using Gardeyn's notion of maximal models as the analogue of regular integral models of varieties. Our main result states that the integral part is contained in the good 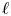 $\ell$-adic part. As opposed to what is expected in the number field setting, we show that the two approaches do not match in general. We conclude this work by introducing the submodule of regulated extensions of mixed Anderson
$\ell$-adic part. As opposed to what is expected in the number field setting, we show that the two approaches do not match in general. We conclude this work by introducing the submodule of regulated extensions of mixed Anderson 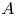 $A$-motives, for which we expect the two approaches to match, and solve some particular cases of this expectation.
$A$-motives, for which we expect the two approaches to match, and solve some particular cases of this expectation.