Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T03:01:08.517Z Has data issue: false hasContentIssue false
  • English
  • Français

On the gcd of local Rankin–Selberg integrals for even orthogonal groups

Part of: Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  20 December 2012

Eyal Kaplan
Eyal Kaplan*
Affiliation:
School of Mathematical Sciences, Sackler Faculty of Exact Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the Rankin–Selberg integral for a pair of representations of 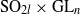${\rm SO}_{2l}\times {\rm GL}_{n}$, where 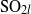${\rm SO}_{2l}$ is defined over a local non-Archimedean field and is either split or quasi-split. The integrals span a fractional ideal, and its unique generator, which contains any pole which appears in the integrals, is called the greatest common divisor (gcd) of the integrals. We describe the properties of the gcd and establish upper and lower bounds for the poles. In the tempered case we can relate it to the 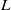$L$-function of the representations defined by Shahidi. Results of this work may lead to a gcd definition for the 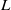$L$-function.

Keywords

Rankin–Selberg integralsgcd$\uppercase {l}$-functions

MSC classification

Secondary: 11S40: Zeta functions and $L$-functions 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 587 - 636
Copyright
Copyright © 2012 The Author(s)

References

[AGRS10]Aizenbud, A., Gourevitch, D., Rallis, S. and Schiffmann, G., Multiplicity one theorems, Ann. of Math. (2) 172 (2010), 1407–1434.Google Scholar
[Ban98]Banks, W., A corollary to Bernstein’s theorem and Whittaker functionals on the metaplectic group, Math. Res. Lett. 5 (1998), 781–790.Google Scholar
[BZ76]Bernstein, I. N. and Zelevinsky, A. V., Representations of the group ${GL(n,F)}$ where ${F}$ is a local non-Archimedean field, Russian Math. Surveys 31 (1976), 1–68.Google Scholar
[BZ77]Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive ${p}$-adic groups I, Ann. Sci. Éc. Norm. Supér. (4) 10 (1977), 441–472.CrossRefGoogle Scholar
[Cas95]Casselman, W., Introduction to the theory of admissible representations of ${p}$-adic reductive groups, Preprint (1995), http://www.math.ubc.ca/∼cass/research/pdf/p-adic-book.pdf.Google Scholar
[CS98]Casselman, W. and Shahidi, F., On irreducibility of standard modules for generic representations, Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 561–589.Google Scholar
[CS80]Casselman, W. and Shalika, J. A., The unramified principal series of ${p}$-adic groups II: the Whittaker function, Compos. Math. 41 (1980), 207–231.Google Scholar
[Cog06]Cogdell, J. W., Lectures on integral representations of ${L}$-functions, Preprint (2006),http://www.math.osu.edu/∼cogdell/columbia-www.pdf (Lecture notes from the instructional workshop: Automorphic Galois Representations, ${L}$-functions and Arithmetic, Columbia University, New York, NY, 17–22 June 2006).Google Scholar
[CP]Cogdell, J. W. and Piatetski-Shapiro, I., Derivatives and L-functions for ${GL_n}$, in The Heritage of B. Moishezon Israel Mathematical Conference Proceedings (Bar-Ilan University, Ramat Gan), to appear, http://www.math.osu.edu/∼cogdell/moish-www.pdf.Google Scholar
[GGP12]Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L-values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), to appear, math.NT/0909.2999v1.Google Scholar
[GPR87]Gelbart, S., Piatetski-Shapiro, I. and Rallis, S., L-functions for G×GL(n), Lecture Notes in Mathematics, vol. 1254 (Springer, New York, NY, 1987).Google Scholar
[Gin90]Ginzburg, D., ${L}$-functions for ${SO_n\times GL_k}$, J. Reine Angew. Math. 405 (1990), 156–180.Google Scholar
[GPR97]Ginzburg, D., Piatetski-Shapiro, I. and Rallis, S., ${L}$-functions for the orthogonal group, Mem. Amer. Math. Soc. 128 (1997).Google Scholar
[HKS96]Harris, M., Kudla, S. S. and Sweet, W. J., Theta dichotomy for unitary groups, J. Amer. Math. Soc. 9 (1996), 941–1004.Google Scholar
[Ike92]Ikeda, T., On the location of poles of the triple L-functions, Compos. Math. 83 (1992), 187–237.Google Scholar
[Ike99]Ikeda, T., On the gamma factor of the triple ${L}$-function, I, Duke Math. J. 97 (1999), 301–318.Google Scholar
[JPS83]Jacquet, H., Piatetski-Shapiro, I. and Shalika, J. A., Rankin-Selberg convolutions, Amer. J. Math. 105 (1983), 367–464.Google Scholar
[Kap10a]Kaplan, E., An invariant theory approach for the unramified computation of Rankin–Selberg integrals for quasi-split ${SO_{2n}\times GL_n}$, J. Number Theory 130 (2010), 1801–1817.Google Scholar
[Kap10b]Kaplan, E., Multiplicativity of the gamma factors of Rankin–Selberg integrals for ${SO_{2l}\times GL_{n}}$, Preprint (2010).Google Scholar
[Kap12]Kaplan, E., The unramified computation of Rankin-Selberg integrals for ${SO_{2l}\times GL_{n}}$, Israel J. Math. 191 (2012), 137–184.Google Scholar
[LM09]Lapid, E. and Mao, Z., On the asymptotics of Whittaker functions, Represent. Theory 13 (2009), 63–81.Google Scholar
[MW10]Moeglin, C. and Waldspurger, J.-L., La conjecture locale de Gross-Prasad pour les groupes spéciaux orthogonaux: le cas général, Preprint (2010), math.RT/1001.0826v1.Google Scholar
[Mui01]Muić, G., A proof of Casselman–Shahidi’s conjecture for quasi-split classical groups, Canad. Math. Bull. 44 (2001), 298–312.CrossRefGoogle Scholar
[Mui04]Muić, G., Reducibility of standard representations for classical ${p}$-adic groups, in Functional analysis VIII (Dubrovnik, 2003), Various Publications Series, vol. 47 (University Aarhus, Aarhus, 2004), 132–145.Google Scholar
[Mui08]Muić, G., A geometric construction of intertwining operators for reductive ${p}$–adic groups, Manuscripta Math. 125 (2008), 241–272.CrossRefGoogle Scholar
[PR86]Piatetski-Shapiro, I. and Rallis, S., ${\epsilon }$ factor of representations of classical groups, Proc. Natl. Acad. Sci. USA 83 (1986), 4589–4593.Google Scholar
[PR87]Piatetski-Shapiro, I. and Rallis, S., Rankin triple ${L}$-functions, Compos. Math. 64 (1987), 31–115.Google Scholar
[Sha78]Shahidi, F., Functional equation satisfied by certain ${L}$-functions, Compos. Math. 37 (1978), 171–208.Google Scholar
[Sha81]Shahidi, F., On certain ${L}$-functions, Amer. J. Math. 103 (1981), 297–355.CrossRefGoogle Scholar
[Sha90]Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series of $\mathfrak {p}$-adic groups, Ann. of Math. (2) 132 (1990), 273–330.CrossRefGoogle Scholar
[Sha92]Shahidi, F., Twisted endoscopy and reducibility of induced representations for ${p}$-adic groups, Duke Math. J. 66 (1992), 1–41.Google Scholar
[Sou93]Soudry, D., Rankin-Selberg convolutions for ${SO_{2l+1}\times GL_n}$: local theory, Mem. Amer. Math. Soc. 105 (1993).Google Scholar
[Sou95]Soudry, D., On the Archimedean theory of Rankin-Selberg convolutions for ${SO_{2l+1}\times GL_{n}}$, Ann. Sci. Éc. Norm. Supér. (4) 28 (1995), 161–224.Google Scholar
[Sou00]Soudry, D., Full multiplicativity of gamma factors for ${SO_{2l+1}\times GL_n}$, Israel J. Math. 120 (2000), 511–561.CrossRefGoogle Scholar
[Wal03]Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques, d’après Harish-Chandra, J. Inst. Math. Jussieu 2 (2003), 235–333.Google Scholar
[Zel80]Zelevinsky, A. V., Induced representations of reductive ${p}$-adic groups II on irreducible representations of ${GL(n)}$, Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 165–210.Google Scholar