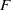Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T23:39:47.596Z Has data issue: false hasContentIssue false
  • English
  • Français

On the $F$-purity of isolated log canonical singularities

Part of: Birational geometry Local theory General commutative ring theory

Published online by Cambridge University Press:  20 June 2013

Osamu Fujino  and
Shunsuke Takagi
Osamu Fujino
Affiliation:
Department of Mathematics, Faculty of Science, Kyoto University, Kyoto 606-8502, Japan email [email protected]
Shunsuke Takagi
Affiliation:
Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo 153-8914, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

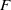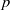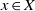A singularity in characteristic zero is said to be of dense $F$-pure type if its modulo $p$ reduction is locally Frobenius split for infinitely many $p$. We prove that if $x\in X$ is an isolated log canonical singularity with 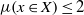$\mu (x\in X)\leq 2$ (where the invariant 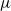$\mu $ is as defined in Definition 1.4), then it is of dense 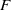$F$-pure type. As a corollary, we prove the equivalence of log canonicity and being of dense 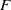$F$-pure type in the case of three-dimensional isolated $ \mathbb{Q} $-Gorenstein normal singularities.

Keywords

log canonical singularitiesF-pure singularities

MSC classification

Secondary: 14B05: Singularities 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 14E30: Minimal model program (Mori theory, extremal rays)
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 9 , September 2013 , pp. 1495 - 1510
Copyright
© The Author(s) 2013 

References

Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.Google Scholar
Bogomolov, F. and Zarhin, Y., Ordinary reduction of $K 3$ surfaces, Cent. Eur. J. Math. 7 (2009), 206–213.Google Scholar
de Fernex, T. and Hacon, C. D., Singularities on normal varieties, Compositio Math. 145 (2009), 393–414.Google Scholar
Fujino, O., Abundance theorem for semi log canonical threefolds, Duke Math. J. 102 (2000), 513–532.Google Scholar
Fujino, O., The indices of log canonical singularities, Amer. J. Math. 123 (2001), 229–253.Google Scholar
Fujino, O., What is log terminal? in Flips for 3-folds and 4-folds, Oxford Lecture Series in Mathematics and its Applications. vol. 35 (Oxford University Press, Oxford, 2007), 49–62.CrossRefGoogle Scholar
Fujino, O., Introduction to the log minimal model program for log canonical pairs, Preprint (2009), arXiv:0907.1506.Google Scholar
Fujino, O., Semi-stable minimal model program for varieties with trivial canonical divisor, Proc. Japan Acad. Ser. A Math. Sci. 87 (2011), 25–30.Google Scholar
Fujino, O., Fundamental theorems for the log minimal model program, Publ. Res. Inst. Math. Sci. 47 (2011), 727–789.Google Scholar
Fujino, O., On isolated log canonical singularities with index one, J. Math. Sci. Univ. Tokyo 18 (2011), 299–323.Google Scholar
Fujino, O., Addendum to ‘On isolated log canonical singularities with index one’, J. Math. Sci. Univ. Tokyo 19 (2012), 131–133.Google Scholar
Hara, N., Classification of two-dimensional $F$-regular and $F$-pure singularities, Adv. Math. 133 (1998), 33–53.Google Scholar
Hara, N., A characterization of rational singularities in terms of injectivity of Frobenius maps, Amer. J. Math. 120 (1998), 981–996.Google Scholar
Hara, N. and Watanabe, K.-i., $F$-regular and $F$-pure rings vs. log terminal and log canonical singularities, J. Algebraic Geom. 11 (2002), 363–392.Google Scholar
Hernández, D., $F$-purity versus log canonicity for polynomials, Preprint (2011), arXiv:1112.2423.Google Scholar
Hochster, M. and Huneke, C., Tight closure and strong $F$-regularity, Mém. Soc. Math. France 38 (1989), 119–133.CrossRefGoogle Scholar
Hochster, M. and Huneke, C., Tight closure in equal characteristic zero, Preprint (1999).Google Scholar
Hochster, M. and Roberts, J., The purity of the Frobenius and local cohomology, Adv. Math. 21 (1976), 117–172.Google Scholar
Ishii, S., On isolated Gorenstein singularities, Math. Ann. 270 (1985), 541–554.CrossRefGoogle Scholar
Ishii, S., A supplement to Fujino’s paper: On isolated log canonical singularities with index one, J. Math. Sci. Univ. Tokyo. 19 (2012), 135–138.Google Scholar
Joshi, K. and Rajan, C. S., Frobenius splitting and ordinarity, Int. Math. Res. Not. (2003), 109–121.Google Scholar
Kollár, J., Sources of log canonical centers, in Minimal models and extremal rays (Kyoto, 2011), Advanced Studies in Pure Mathematics, to appear (American Mathematical Society, Providence, RI).Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998).Google Scholar
Mehta, V. B. and Srinivas, V., Normal $F$-pure surface singularities, J. Algebra 143 (1991), 130–143.Google Scholar
Miller, L. E. and Schwede, K., Semi-log canonical vs $F$-pure singularities, J. Algebra 349 (2012), 150–164.Google Scholar
Mustaţă, M. and Srinivas, V., Ordinary varieties and the comparison between multiplier ideals and test ideals, Nagoya Math. J. 204 (2011), 125–157.Google Scholar
Ogus, A., Hodge cycles and crystalline cohomology, in Hodge cycles, motives, and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1981), 357–414.Google Scholar
Schwede, K. and Smith, K. E., Globally $F$-regular and log Fano varieties, Adv. Math. 224 (2010), 863–894.Google Scholar
Szabó, E., Divisorial log terminal singularities, J. Math. Sci. Univ. Tokyo 1 (1995), 631–639.Google Scholar
Takagi, S., Adjoint ideals and a correspondence between log canonicity and F-purity, Algebra Number Theory, to appear, arXiv:1105.0072.Google Scholar
Watanabe, K.-i., Study of $F$-purity in dimension two, in Algebraic geometry and commutative algebra, Vol. II (Kinokuniya, Tokyo, 1988), 791–800.Google Scholar
Watanabe, K.-i., $F$-regular and $F$-pure normal graded rings, J. Pure Appl. Algebra 71 (1991), 341–350.CrossRefGoogle Scholar