On the determinant bundles of abelian schemes

Vincent Maillot; Damian Rössler

doi:10.1112/S0010437X07003235

On the determinant bundles of abelian schemes

Part of: Abelian varieties and schemes Cycles and subschemes

Published online by Cambridge University Press: 01 March 2008

Vincent Maillot and

Damian Rössler

Show author details

Vincent Maillot: Affiliation:
Institut de Mathématiques de Jussieu, Université Paris 7 Denis Diderot, C.N.R.S., Case Postale 7012, 2 place Jussieu, F-75251 Paris cedex 05, France (email: [email protected], [email protected])
Damian Rössler: Affiliation:
Institut de Mathématiques de Jussieu, Université Paris 7 Denis Diderot, C.N.R.S., Case Postale 7012, 2 place Jussieu, F-75251 Paris cedex 05, France (email: [email protected], [email protected])

Article contents

Abstract

Rights & Permissions

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 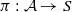be an abelian scheme over a scheme S which is quasi-projective over an affine noetherian scheme and let 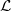be a symmetric, rigidified, relatively ample line bundle on 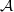. We show that there is an isomorphism 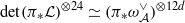of line bundles on S, where d is the rank of the (locally free) sheaf 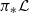. We also show that the numbers 24 and 12d are sharp in the following sense: if N>1 is a common divisor of 12 and 24, then there are data as above such that