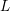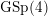Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Torzewski, Alex
2020.
Functoriality of motivic lifts of the canonical construction.
manuscripta mathematica,
Vol. 163,
Issue. 1-2,
p.
27.
Grossi, Giada
2020.
On norm relations for Asai–Flach classes.
International Journal of Number Theory,
Vol. 16,
Issue. 10,
p.
2311.
Lemma, Francesco
2020.
Algebraic Cycles and Residues of Degree 8 L-functions of GSp(4) × GL(2).
International Mathematics Research Notices,
Vol. 2020,
Issue. 12,
p.
3614.
Loeffler, David
Pilloni, Vincent
Skinner, Christopher
and
Zerbes, Sarah Livia
2021.
Higher Hida theory and p-adic L-functions for GSp4.
Duke Mathematical Journal,
Vol. 170,
Issue. 18,
Lemma, Francesco
and
Ochiai, Tadashi
2023.
Endoscopic congruences modulo adjoint L-values for GSp(4).
Kyoto Journal of Mathematics,
Vol. 63,
Issue. 2,
Graham, Andrew
and
Shah, Syed Waqar Ali
2023.
Anticyclotomic Euler systems for unitary groups.
Proceedings of the London Mathematical Society,
Vol. 127,
Issue. 6,
p.
1577.
Cauchi, Antonio
Lemma, Francesco
and
Jacinto, Joaquín Rodrigues
2025.
On higher regulators of Siegel varieties.
Journal de théorie des nombres de Bordeaux,
Vol. 36,
Issue. 3,
p.
767.
Cauchi, Antonio
Lemma, Francesco
and
Rodrigues Jacinto, Joaquín
2025.
Algebraic cycles and functorial lifts from G2 to
PGSp6.
Algebra & Number Theory,
Vol. 19,
Issue. 3,
p.
551.