Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-05-02T19:46:57.717Z Has data issue: false hasContentIssue false
  • English
  • Français

On Donkin's tilting module conjecture II: counterexamples

Part of: Lie algebras and Lie superalgebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  02 May 2024

Christopher P. Bendel ,
Daniel K. Nakano ,
Cornelius Pillen  and
Paul Sobaje
Christopher P. Bendel
Affiliation:
Department of Mathematics, Statistics and Computer Science, University of Wisconsin-Stout, Menomonie, WI 54751, USA [email protected]
Daniel K. Nakano
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, USA [email protected]
Cornelius Pillen
Affiliation:
Department of Mathematics and Statistics, University of South Alabama, Mobile, AL 36688, USA [email protected]
Paul Sobaje
Affiliation:
Department of Mathematical Sciences, Georgia Southern University, Statesboro, GA 30458, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we produce infinite families of counterexamples to Jantzen's question posed in 1980 on the existence of Weyl 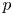$p$-filtrations for Weyl modules for an algebraic group and Donkin's tilting module conjecture formulated in 1990. New techniques to exhibit explicit examples are provided along with methods to produce counterexamples in large rank from counterexamples in small rank. Counterexamples can be produced via our methods for all groups other than when the root system is of type 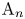${\rm A}_{n}$ or 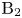${\rm B}_{2}$.

Keywords

tilting modulesalgebraic groupsrepresentation theory

MSC classification

Primary: 20G05: Representation theory 20G10: Cohomology theory
Secondary: 17B10: Representations, algebraic theory (weights)
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 6 , June 2024 , pp. 1167 - 1193
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Research of the first author was supported in part by Simons Foundation Collaboration Grant 317062. Research of the second author was supported in part by NSF grants DMS-1701768 and DMS-2101941. Research of the third author was supported in part by Simons Foundation Collaboration Grant 245236.

References

Andersen, H. H., Extensions of modules for algebraic groups, Amer. J. Math. 106 (1984), 498–504.CrossRefGoogle Scholar
Andersen, H. H., $p$-filtrations of dual Weyl modules, Adv. Math. 352 (2019), 231–245.CrossRefGoogle Scholar
Bendel, C. P., Nakano, D. K. and Pillen, C., Extensions for Frobenius kernels, J. Algebra 272 (2004), 476–511.CrossRefGoogle Scholar
Bendel, C. P., Nakano, D. K., Pillen, C. and Sobaje, P., On tensoring with the Steinberg representation, Transform. Groups 25 (2020), 981–1008.CrossRefGoogle Scholar
Bendel, C. P., Nakano, D. K., Pillen, C. and Sobaje, P., Counterexamples to the tilting and $(p,r)$-filtration conjectures, J. Reine Angew. Math. 767 (2020), 193–202.CrossRefGoogle Scholar
Bendel, C. P., Nakano, D. K., Pillen, C. and Sobaje, P., On Donkin's tilting module conjecture I: lowering the prime, Represent. Theory 26 (2022), 455–497.CrossRefGoogle Scholar
Bendel, C. P., Nakano, D. K., Pillen, C. and Sobaje, P., On Donkin's tilting module conjecture III: new generic lower bounds, J. Algebra, doi:10.1016/j.jalgebra.2023.07.001.Google Scholar
Donkin, S., A note on decomposition numbers of reductive algebraic groups, J. Algebra 80 (1983), 226–234.CrossRefGoogle Scholar
Donkin, S., On tilting modules for algebraic groups, Math. Z. 212 (1993), 39–60.CrossRefGoogle Scholar
Doty, S., GAP: Weyl Modules, Version 1.1 (2009), https://doty.math.luc.edu/weyl/version_1.1/manual.pdf.Google Scholar
Dowd, M. F. and Sin, P., On representations of algebraic groups in characteristic $2$, Comm. Algebra 28 (1996), 2597–2686.CrossRefGoogle Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.11.1 (2021), https://www.gap-system.org.Google Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory, Graduate Texts in Mathematics (Springer, New York, 1972).CrossRefGoogle Scholar
Humphreys, J. E. and Verma, D. N., Projective modules for finite Chevalley groups, Bull. Amer. Math. Soc. (N.S.) 79 (1973), 467–468.CrossRefGoogle Scholar
Jantzen, J. C., Darstellungen halbeinfacher Gruppen und ihrer Frobenius-Kerne, J. Reine Angew. Math. 317 (1980), 157–199.Google Scholar
Jantzen, J. C., First cohomology groups for classical lie algebras, Progress in Mathematics, vol. 95 (Birkhäuser, Basel, 1991).Google Scholar
Jantzen, J. C., Representations of algebraic groups, second edition, Mathematical Surveys and Monographs, vol. 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kildetoft, T. and Nakano, D. K., On good $(p,r)$ filtrations for rational $G$-modules, J. Algebra 423 (2015), 702–725.CrossRefGoogle Scholar
van Leeuwen, M. A. A., Cohen, A. M. and Lisser, B., LiE, A package for Lie group computations (Computer Algebra Nederland, Amsterdam, 1992).Google Scholar
Lübeck, F., Tables of weight multiplicities, http://www.math.rwth-aachen.de/~Frank.Luebeck/chev/WMSmall/index.html.Google Scholar
Parshall, B. J. and Scott, L. L., On $p$-filtrations of Weyl modules, J. Lond. Math. Soc. (2) 91 (2015), 127–158.CrossRefGoogle Scholar
Pillen, C., Tensor products of modules with restricted highest weight, Comm. Algebra 21 (1993), 3647–3661.CrossRefGoogle Scholar
Sin, P., Extensions of simple modules for special algebraic groups, J. Algebra 170 (1994), 1011–1034.CrossRefGoogle Scholar
Sobaje, P., On $(p,r)$-filtrations and tilting modules, Proc. Amer. Math. Soc. 146 (2018), 1951–1961.CrossRefGoogle Scholar
Sobaje, P., The Steinberg quotient of a tilting character, Math. Z. 297 (2021), 1733–1747.CrossRefGoogle Scholar