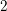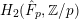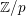Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ivanov, Sergei
and
Mikhailov, Roman
2019.
A finite ℚ–bad space.
Geometry & Topology,
Vol. 23,
Issue. 3,
p.
1237.
Ivanov, Sergei O.
Mikhailov, Roman
and
Zaikovskii, Anatolii
2020.
Homological properties of parafree Lie algebras.
Journal of Algebra,
Vol. 560,
Issue. ,
p.
1092.
Ivanov, Sergei O.
and
Lopatkin, Viktor
2021.
Parafree augmented algebras and Gröbner-Shirshov bases for complete augmented algebras.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 11,
p.
106725.
Ivanov, Sergei O.
and
Mikhailov, Roman
2023.
HR-length of a free group via polynomial functors.
Journal of Pure and Applied Algebra,
Vol. 227,
Issue. 12,
p.
107443.
Basok, Mikhail
Ivanov, Sergei O.
and
Mikhailov, Roman
2024.
Homology of the pronilpotent completion and cotorsion groups.
Israel Journal of Mathematics,
Vol. 261,
Issue. 1,
p.
281.