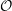 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutionsPublished online by Cambridge University Press: 07 September 2017
In this paper we study categories 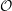 ${\mathcal{O}}$ over quantizations of symplectic resolutions admitting Hamiltonian tori actions with finitely many fixed points. In this generality, these categories were introduced by Braden et al. We establish a family of standardly stratified structures (in the sense of the author and Webster) on these categories
${\mathcal{O}}$ over quantizations of symplectic resolutions admitting Hamiltonian tori actions with finitely many fixed points. In this generality, these categories were introduced by Braden et al. We establish a family of standardly stratified structures (in the sense of the author and Webster) on these categories 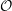 ${\mathcal{O}}$ . We use these structures to study shuffling functors of Braden et al. (called cross-walling functors in this paper). Most importantly, we prove that all cross-walling functors are derived equivalences that define an action of the Deligne groupoid of a suitable real hyperplane arrangement.
${\mathcal{O}}$ . We use these structures to study shuffling functors of Braden et al. (called cross-walling functors in this paper). Most importantly, we prove that all cross-walling functors are derived equivalences that define an action of the Deligne groupoid of a suitable real hyperplane arrangement.