Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T20:13:58.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Odd zeta motive and linear forms in odd zeta values

Part of: Arithmetic problems. Diophantine geometry (Co)homology theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  30 October 2017

Clément Dupont
Clément Dupont*
Affiliation:
Institut Montpelliérain Alexander Grothendieck, CNRS, Univ. Montpellier, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a family of mixed Tate motives over 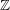$\mathbb{Z}$ whose periods are linear forms in the zeta values 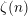$\unicode[STIX]{x1D701}(n)$. They naturally include the Beukers–Rhin–Viola integrals for 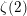$\unicode[STIX]{x1D701}(2)$ and the Ball–Rivoal linear forms in odd zeta values. We give a general integral formula for the coefficients of the linear forms and a geometric interpretation of the vanishing of the coefficients of a given parity. The main underlying result is a geometric construction of a minimal ind-object in the category of mixed Tate motives over 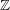$\mathbb{Z}$ which contains all the non-trivial extensions between simple objects. In a joint appendix with Don Zagier, we prove the compatibility between the structure of the motives considered here and the representations of their periods as sums of series.

Keywords

zeta valuesmixed Tate motives

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 14F42: Motivic cohomology; motivic homotopy theory 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 2 , February 2018 , pp. 342 - 379
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apéry, R., Irrationalité de 𝜁(2) et 𝜁(3) , Astérisque 61 (1979), 11–13.Google Scholar
Ball, K. and Rivoal, T., Irrationalité d’une infinité de valeurs de la fonction zêta aux entiers impairs , Invent. Math. 146 (2001), 193–207.Google Scholar
Beukers, F., A note on the irrationality of 𝜁(2) and 𝜁(3) , Bull. Lond. Math. Soc. 11 (1979), 268–272.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher K-theory , Adv. Math. 61 (1986), 267–304.CrossRefGoogle Scholar
Borel, A., Cohomologie de SL n et valeurs de fonctions zeta aux points entiers , Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 4 (1977), 613–636.Google Scholar
Brown, F., Irrationality proofs for zeta values, moduli spaces and dinner parties , Mosc. J. Comb. Number Theory 6 (2016), 102–165.Google Scholar
Cresson, J., Fischler, S. and Rivoal, T., Phénomènes de symétrie dans des formes linéaires en polyzêtas , J. Reine Angew. Math. 617 (2008), 109–151.Google Scholar
Cresson, J., Fischler, S. and Rivoal, T., Séries hypergéométriques multiples et polyzêtas , Bull. Soc. Math. France 136 (2008), 97–145.Google Scholar
Deligne, P., Théorie de Hodge II , Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.Google Scholar
Deligne, P., Théorie de Hodge III , Publ. Math. Inst. Hautes Études Sci. 44 (1974), 5–77.Google Scholar
Deligne, P., Le groupe fondamental de la droite projective moins trois points , in Galois groups over Q , Berkeley, CA, 1987, Mathematical Sciences Research Institute Publications, vol. 16 (Springer, New York, NY, 1989), 79–297.Google Scholar
Deligne, P. and Goncharov, A. B., Groupes fondamentaux motiviques de Tate mixte , Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 1–56.CrossRefGoogle Scholar
Dupont, C., Relative cohomology of bi-arrangements , Trans. Amer. Math. Soc. 369 (2017), 8105–8160.Google Scholar
Fischler, S., Irrationalité de valeurs de zêta (d’après Apéry, Rivoal, …) , Astérisque 294 (2004), vii, 27–62.Google Scholar
Foata, D., Distributions eulériennes et mahoniennes sur le groupe des permutations , in Higher combinatorics: Proc. NATO Advanced Study Institute, Berlin, 1976, NATO Advanced Study Institutes Series, Series C, vol. 31 (Reidel, Dordrecht, 1977), 27–49.Google Scholar
Foata, D., Eulerian polynomials: from Euler’s time to the present , in The legacy of Alladi Ramakrishnan in the mathematical sciences (Springer, New York, 2010), 253–273.Google Scholar
Goncharov, A. B., Periods and mixed motives, Preprint (2002), arXiv:math.AG/0202154.Google Scholar
Goncharov, A. B. and Manin, Yu. I., Multiple 𝜁-motives and moduli spaces M 0, n , Compos. Math. 140 (2004), 1–14.Google Scholar
Hatcher, A., Algebraic topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Huber, A., Realization of Voevodsky’s motives , J. Algebraic Geom. 9 (2000), 755–799.Google Scholar
Huber, A., Corrigendum to: “Realization of Voevodsky’s motives” [J. Algebraic Geom.] 9 (2000) 755–799; mr1775312 , J. Algebraic Geom. 13 (2004), 195–207.Google Scholar
Levine, M., Tate motives and the vanishing conjectures for algebraic K-theory , in Algebraic K-theory and algebraic topology Lake Louise, AB, 1991, NATO Advanced Study Institutes Series, Series C, vol. 407 (Kluwer Academic, Dordrecht, 1993), 167–188.Google Scholar
Rivoal, T., La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs , C. R. Acad. Sci. Paris Sér. I Math. 331 (2000), 267–270.Google Scholar
Rhin, G. and Viola, C., On a permutation group related to 𝜁(2) , Acta Arith. 77 (1996), 23–56.Google Scholar
Rhin, G. and Viola, C., The group structure for 𝜁(3) , Acta Arith. 97 (2001), 269–293.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field , in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Zudilin, W., Arithmetic of linear forms involving odd zeta values , J. Théor. Nombres Bordeaux 16 (2004), 251–291.Google Scholar