Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Dawei
2011.
Square-tiled surfaces and rigid curves on moduli spaces.
Advances in Mathematics,
Vol. 228,
Issue. 2,
p.
1135.
Arap, Maxim
Gibney, Angela
Stankewicz, James
and
Swinarski, David
2012.
sln Level 1 Conformal Blocks Divisors on M̄0,n.
International Mathematics Research Notices,
Vol. 2012,
Issue. 7,
p.
1634.
Pixton, Aaron
2013.
A nonboundary nef divisor on M0,12.
Geometry & Topology,
Vol. 17,
Issue. 3,
p.
1317.
Grushevsky, S.
and
Salvati Manni, R.
2013.
The Prym Map on Divisors, and the Slope of A5.
International Mathematics Research Notices,
Alexeev, Valery
Gibney, Angela
and
Swinarski, David
2014.
Higher-Level Conformal Blocks Divisors on .
Proceedings of the Edinburgh Mathematical Society,
Vol. 57,
Issue. 1,
p.
7.
Liu, Xiao-Lei
2016.
Curves with prescribed intersection with boundary divisors in moduli spaces of curves.
Pacific Journal of Mathematics,
Vol. 283,
Issue. 2,
p.
365.
Hyeon, Donghoon
2017.
An Outline of the Log Minimal Model Program for the Moduli Space of Curves.
Experimental Mathematics,
Vol. 26,
Issue. 1,
p.
114.
Moon, Han-Bom
Summers, Charles
von Albade, James
and
Xie, Ranze
2018.
Birational contractions of $$\overline{\mathrm {M}}_{0,n}$$ M ¯ 0 , n and combinatorics of extremal assignments.
Journal of Algebraic Combinatorics,
Vol. 47,
Issue. 1,
p.
51.
Moon, Han-Bom
and
Swinarski, David
2019.
On the S-invariant F-conjecture.
Journal of Algebra,
Vol. 517,
Issue. ,
p.
439.
Castravet, Ana-Maria
Laface, Antonio
Tevelev, Jenia
and
Ugaglia, Luca
2023.
Blown-up toric surfaces with non-polyhedral effective cone.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Chen, L.
Gibney, A.
Heller, L.
Kalashnikov, E.
Larson, H.
and
Xu, W.
2024.
On an Equivalence of Divisors on $\overline {\text {M}}_{0,n}$ from Gromov-Witten Theory and Conformal Blocks.
Transformation Groups,
Vol. 29,
Issue. 2,
p.
561.


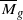 to be ample
to be ample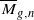 of
of 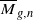
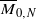 for
for 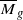 is known to be of general type.
is known to be of general type.