Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T01:18:51.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-rigid quartic 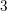$3$-folds

Part of: Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  22 December 2015

Hamid Ahmadinezhad  and
Anne-Sophie Kaloghiros
Hamid Ahmadinezhad
Affiliation:
School of Mathematics, University of Bristol, BristolBS8 1TW, UK email [email protected]
Anne-Sophie Kaloghiros
Affiliation:
Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK email [email protected] Current address:Brunel University London, Uxbridge UB8 3PH, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 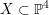$X\subset \mathbb{P}^{4}$ be a terminal factorial quartic 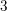$3$-fold. If 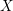$X$ is non-singular, 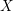$X$ is birationally rigid, i.e. the classical minimal model program on any terminal 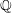$\mathbb{Q}$-factorial projective variety 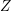$Z$ birational to 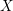$X$ always terminates with 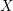$X$. This no longer holds when 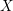$X$ is singular, but very few examples of non-rigid factorial quartics are known. In this article, we first bound the local analytic type of singularities that may occur on a terminal factorial quartic hypersurface 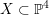$X\subset \mathbb{P}^{4}$. A singular point on such a hypersurface is of type 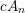$cA_{n}$ (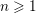$n\geqslant 1$), or of type 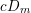$cD_{m}$ (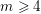$m\geqslant 4$) or of type 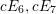$cE_{6},cE_{7}$ or 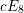$cE_{8}$. We first show that if 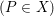$(P\in X)$ is of type 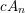$cA_{n}$, $n$ is at most 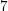$7$ and, if 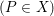$(P\in X)$ is of type 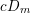$cD_{m}$, 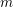$m$ is at most 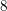$8$. We then construct examples of non-rigid factorial quartic hypersurfaces whose singular loci consist (a) of a single point of type 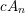$cA_{n}$ for 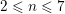$2\leqslant n\leqslant 7$, (b) of a single point of type 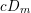$cD_{m}$ for 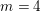$m=4$ or 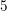$5$ and (c) of a single point of type 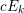$cE_{k}$ for 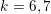$k=6,7$ or 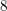$8$.

Keywords

birational mapsquartic hypersurfacesbirational rigidity

MSC classification

Primary: 14E05: Rational and birational maps 14J30: $3$-folds 14J45: Fano varieties
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 5 , May 2016 , pp. 955 - 983
Creative Commons
Creative Common License - CCCreative Common License - BY
This article is distributed with Open Access under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided that the original work is properly cited.
Copyright
© The Authors 2015

References

Ahmadinezhad, H., On del Pezzo fibrations that are not birationally rigid, J. Lond. Math. Soc. (2) 86 (2012), 36–62; MR 2959294.CrossRefGoogle Scholar
Ahmadinezhad, H., On pliability of del Pezzo fibrations and Cox rings, J. reine angew. Math. (2014), doi:10.1515/crelle-2014-0095.Google Scholar
Arnol’d, V. I., Guseĭn-Zade, S. M. and Varchenko, A. N., Singularities of differentiable maps: Vol. I: the classification of critical points, caustics and wave fronts, Monographs in Mathematics, vol. 82 (Birkhäuser, Boston, MA, 1985); translated from the Russian by Ian Porteous and Mark Reynolds.Google Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.Google Scholar
Brown, G., Flips arising as quotients of hypersurfaces, Math. Proc. Cambridge Philos. Soc. 127 (1999), 13–31.Google Scholar
Corti, A., Factoring birational maps of threefolds after Sarkisov, J. Algebraic Geom. 4 (1995), 223–254.Google Scholar
Corti, A. and Mella, M., Birational geometry of terminal quartic 3-folds. I, Amer. J. Math. 126 (2004), 739–761.Google Scholar
Corti, A., Pukhlikov, A. and Reid, M., Fano 3-fold hypersurfaces, in Explicit birational geometry of 3-folds, London Mathematical Society Lecture Note Series, vol. 281 (Cambridge University Press, Cambridge, 2000), 175–258.Google Scholar
The graded ring database, http://www.grdb.co.uk/.Google Scholar
Hacon, C. D. and McKernan, J., The Sarkisov program, J. Algebraic Geom. 22 (2013), 389–405.Google Scholar
Hu, Y. and Keel, S., Mori dream spaces and GIT, Michigan Math. J. 48 (2000), 331–348.Google Scholar
Iskovskikh, V. A. and Manin, Ju. I., Three-dimensional quartics and counterexamples to the Lüroth problem, Mat. Sb. (N.S.) 86 (1971), 140–166.Google Scholar
Iskovskikh, V. A. and Prokhorov, Yu. G., Fano varieties, in Algebraic geometry, V, Encyclopaedia of Mathematical Sciences, vol. 47 (Springer, Berlin, 1999), 1–247.Google Scholar
Kaloghiros, A.-S., The defect of Fano 3-folds, J. Algebraic Geom. 20 (2011), 127–149.Google Scholar
Kaloghiros, A.-S., A classification of terminal quartic 3-folds and applications to rationality questions, Math. Ann. 354 (2012), 263–296.Google Scholar
Kaloghiros, A.-S., Relations in the Sarkisov program, Compositio Math. 149 (2013), 1685–1709.Google Scholar
Kaloghiros, A.-S., Küronya, A. and Lazić, V., Finite generation and geography of models, in Minimal models and extremal rays, Advanced Studies in Pure Mathematics (Mathematical Society of Japan, Tokyo, 2014), to appear.Google Scholar
Kawakita, M., Divisorial contractions in dimension three which contract divisors to smooth points, Invent. Math. 145 (2001), 105–119.Google Scholar
Kawakita, M., Divisorial contractions in dimension three which contract divisors to compound A 1 points, Compositio Math. 133 (2002), 95–116.Google Scholar
Kawakita, M., General elephants of three-fold divisorial contractions, J. Amer. Math. Soc. 16 (2003), 331–362 (electronic).Google Scholar
Kollár, J., Real algebraic threefolds. I. Terminal singularities, Collect. Math. 49 (1998), 335–360; dedicated to the memory of Fernando Serrano.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998).Google Scholar
Markushevich, D., Minimal discrepancy for a terminal cDV singularity is 1, J. Math. Sci. Univ. Tokyo 3 (1996), 445–456.Google Scholar
Mella, M., Birational geometry of quartic 3-folds. II. The importance of being ℚ-factorial, Math. Ann. 330 (2004), 107–126.Google Scholar
Namikawa, Y., Smoothing Fano 3-folds, J. Algebraic Geom. 6 (1997), 307–324.Google Scholar
Namikawa, Y. and Steenbrink, J. H. M., Global smoothing of Calabi–Yau threefolds, Invent. Math. 122 (1995), 403–419.Google Scholar
Pettersen, K. F., On nodal determinantal quartic hypersurfaces in $\mathbf{P}^{4}$, PhD thesis, University of Oslo (1998).Google Scholar
Reid, M., Young person’s guide to canonical singularities, in Algebraic geometry (Bowdoin, Brunswick, Maine, 1985), Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 345–414.Google Scholar
Todd, J. A., Configurations defined by six lines in space of three dimensions, Math. Proc. Cambridge Philos. Soc. 29 (1933), 52–68.Google Scholar
Todd, J. A., A note on two special primals in four dimensions, Q. J. Math. 6 (1935), 129–136.Google Scholar
Todd, J. A., On a quartic primal with forty-five nodes, in space of four dimensions, Q. J. Math. 7 (1936), 169–174.Google Scholar