Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-05T08:45:18.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-abelian Cohen–Lenstra heuristics over function fields

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  12 May 2017

Nigel Boston  and
Melanie Matchett Wood
Nigel Boston
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, 480 Lincoln Drive, Madison, WI 53706, USA email [email protected]
Melanie Matchett Wood
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, 480 Lincoln Drive, Madison, WI 53706, USA American Institute of Mathematics, 600 East Brokaw Road, San Jose, CA 95112, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

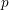Boston, Bush and Hajir have developed heuristics, extending the Cohen–Lenstra heuristics, that conjecture the distribution of the Galois groups of the maximal unramified pro-$p$ extensions of imaginary quadratic number fields for 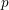$p$ an odd prime. In this paper, we find the moments of their proposed distribution, and further prove there is a unique distribution with those moments. Further, we show that in the function field analog, for imaginary quadratic extensions of 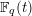$\mathbb{F}_{q}(t)$, the Galois groups of the maximal unramified pro-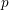$p$ extensions, as $q\rightarrow \infty$, have the moments predicted by the Boston, Bush and Hajir heuristics. In fact, we determine the moments of the Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic function fields, leading to a conjecture on Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic number fields.

Keywords

Cohen–Lenstra heuristicsp-class tower groupsunramified extensionsquadratic fields

MSC classification

Primary: 11G20: Curves over finite and local fields 11R11: Quadratic extensions 11R29: Class numbers, class groups, discriminants 11R58: Arithmetic theory of algebraic function fields 11R45: Density theorems
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 7 , July 2017 , pp. 1372 - 1390
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adam, M. and Malle, G., A class group heuristic based on the distribution of 1-eigenspaces in matrix groups , J. Number Theory 149 (2015), 225–235.Google Scholar
Bhargava, M., The geometric sieve and the density of squarefree values of invariant polynomials, Preprint (2014), arXiv:1402.0031.Google Scholar
Boston, N., Explicit deformation of Galois representations , Invent. Math. 103 (1991), 181–196.Google Scholar
Boston, N., Bush, M. and Hajir, F., Heuristics for $p$ -class towers of imaginary quadratic fields, Math. Ann. (2016), 1–37; doi:10.1007/s00208-016-1449-3.Google Scholar
Boston, N. and Nover, H., Computing pro-p Galois groups , in Algorithmic number theory, Proc. 7th int. symposium, ANTS-VII, Berlin, July 23–28, 2006 (Springer, 2006), 1–10.Google Scholar
Clancy, J., Kaplan, N., Leake, T., Payne, S. and Wood, M. M., On a Cohen–Lenstra heuristic for Jacobians of random graphs , J. Algebraic Combin. 42 (2015), 701–723.Google Scholar
Cohen, H. and Lenstra, H. W. Jr, Heuristics on class groups of number fields , in Number theory, Noordwijkerhout 1983, Lecture Notes in Mathematics, vol. 1068 (Springer, Berlin, 1984), 33–62.CrossRefGoogle Scholar
Ellenberg, J., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen Lenstra conjecture over function fields, II, Preprint (2012), arXiv:1212.0923.Google Scholar
Ellenberg, J. S., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen–Lenstra conjecture over function fields , Ann. of Math. (2) 183 (2016), 729–786.CrossRefGoogle Scholar
Friedman, E. and Washington, L. C., On the distribution of divisor class groups of curves over a finite field , in Théorie des nombres, Quebec, 1987 (de Gruyter, Berlin, 1989), 227–239.Google Scholar
Garton, D., Random matrices, the Cohen–Lenstra heuristics, and roots of unity , Algebra Number Theory 9 (2015), 149–171.Google Scholar
Gorenstein, D., Finite groups, AMS Chelsea Publishing Series (American Mathematical Society, Providence, RI, 2007).Google Scholar
Gruenberg, K. W., Relation modules of finite groups, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, vol. 25 (American Mathematical Society, Providence, RI, 1976).Google Scholar
Hajir, F. and Maire, C., Asymptotically good towers of global fields , in 3rd European congress of mathematics (ECM), Vol. II, Barcelona, Spain, July 10–14, 2000, Progress in Mathematics, vol. 202, eds Casacuberta, C. et al. (Birkhäuser, Basel, 2001), 207–218.Google Scholar
Hall, P., A contribution to the theory of groups of prime-power order , Proc. Lond. Math. Soc. (2) 36 (1934), 29–95.Google Scholar
Koch, H. and Venkov, B. B., Über den p-Klassenkörperturm eines imaginär-quadratischen Zahlkörpers , Astèrisque 24–25 (1975), 57–67.Google Scholar
Malle, G., Cohen–Lenstra heuristic and roots of unity , J. Number Theory 128 (2008), 2823–2835.Google Scholar
O’Brien, E. A., The p-group generation algorithm , J. Symbolic Comput. 9 (1990), 677–698.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas, Tome 3, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Lecture Notes in Mathematics, vol. 305 (Springer, New York, NY, 1973); avec la collaboration de P. Deligne et B. Saint-Donat.Google Scholar
Wilson, J. S., Profinite groups (Clarendon Press, Oxford, 1998).Google Scholar