Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T21:59:19.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Motivic cohomology spectral sequence and Steenrod operations

Part of: $K$-theory in geometry Operations and obstructions Spectral sequences (Co)homology theory

Published online by Cambridge University Press:  24 June 2016

Serge Yagunov
Serge Yagunov*
Affiliation:
Steklov Mathematical Institute (St. Petersburg), Fontanka, 27, St. Petersburg, 191023, Russia Max-Planck-Institut für Mathematik, Vivatsgasse, 7, 53111, Bonn, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a prime number 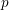$p$ , we show that differentials 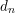$d_{n}$ in the motivic cohomology spectral sequence with 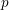$p$ -local coefficients vanish unless 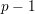$p-1$ divides 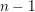$n-1$ . We obtain an explicit formula for the first non-trivial differential 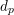$d_{p}$ , expressing it in terms of motivic Steenrod 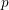$p$ -power operations and Bockstein maps. To this end, we compute the algebra of operations of weight 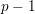$p-1$ with 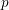$p$ -local coefficients. Finally, we construct examples of varieties having non-trivial differentials 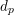$d_{p}$ in their motivic cohomology spectral sequences.

Keywords

motivic cohomological operationsSteenrod algebramotivic cohomology spectral sequence

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 19E20: Relations with cohomology theories
Secondary: 55S10: Steenrod algebra 55T99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 10 , October 2016 , pp. 2113 - 2133
Copyright
© The Author 2016 

References

Adams, J. F., On the groups J(X)-II , Topology 3 (1965), 137–171.Google Scholar
Artin, M., Grothendieck topologies, Lecture Notes (Harvard University Mathematics Department, Cambridge, MA, 1962).Google Scholar
Bloch, S. and Lichtenbaum, S., A spectral sequence for motivic cohomology, Preprint (1995),www.math.uiuc.edu/K-theory/0062.Google Scholar
Бухштабер, В. М., Модули дифференциалов спеҡтральной последовательности Атья–Хирцебруха , Матем. сб. 78 (1969), 307–320; English translation: V. M. Buchstaber, Modules of differentials of the Atiyah–Hirzebruch spectral sequence, Math. USSR Sb. 7 (1969), 299–313.Google Scholar
Cartan, H., Algèbres d’Eilenberg–Mac Lane et homotopie , Séminaire H. Cartan, ENS 7(1) (1954–1955), Exposé 9.Google Scholar
Deligne, P., Voevodsky’s lectures on motivic cohomology 2000/2001 , in Algebraic topology. The Abel symposium, 2007 (Springer, Berlin, Heidelberg, 2009), 355–409.Google Scholar
Friedlander, E. and Suslin, A., The spectral sequence relating algebraic K-theory to motivic cohomology , Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 773–875.Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology, Cambridge Studies in Advanced Mathematics, vol. 101 (Cambridge University Press, Cambridge, 2006).Google Scholar
Gillet, H. and Soulé, C., Filtrations on higher algebraic K-theory , Proc. Sympos. Pure Math. 67 (1999), 89–148.Google Scholar
Grayson, D., Weight filtrations via commuting automorphisms , K-Theory 9 (1995), 139–172.Google Scholar
Hoyois, M., Kelly, S. and Østvær, P. A., The motivic Steenrod algebra in positive characteristic, J. Eur. Math. Soc., to appear; arXiv:1305.5690v2.Google Scholar
Kervaire, M. and Milnor, J., Bernoulli numbers, homotopy groups, and a theorem of Rohlin , Proceedings of International Congress of Mathematicians, vol. 1958 (Cambridge University Press, New York, 1960), 454–458.Google Scholar
Levine, M., The homotopy coniveau tower , J. Topol. 1 (2008), 217–267.Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Merkurjev, A., Adams operations and the Brown–Gersten–Quillen spectral sequence , in Quadratic forms, linear algebraic groups, and cohomology, Developments in Mathematics vol. 18 (Springer, New York, 2010), 305–313.Google Scholar
Merkurjev, A. and Suslin, A., K-cohomology of Severi–Brauer varieties and the norm residue homomorphism , Izv. Akad. Nauk SSSR Ser. Mat. 46 (1982), 1011–1046.Google Scholar
Panin, I. A., On algebraic K-theory of generalized flag fiber bundles and some of their twisted forms , in Algebraic K-theory, Advances in Soviet Mathematics, vol. 4 (American Mathematical Society, Providence, RI, 1991), 21–46.Google Scholar
Quillen, D., Higher algebraic K-theory I, Lecture Notes in Mathematics, vol. 341 (Springer, Berlin, Heidelberg, 1973), 85–147.Google Scholar
Riou, J., Algebraic K-theory, A 1 -homotopy and Riemann–Roch theorems , J. Topol. 3 (2010), 229–264.Google Scholar
Rost, M., Chow groups with coefficients , Doc. Math. 1 (1996), 319–393; (electronic).Google Scholar
Röndigs, O. and Østvær, P. A., Modules over motivic cohomology , Adv. Math. 219 (2008), 689–727.Google Scholar
Suslin, A., K-theory and K-cohomology of certain group varieties , in Algebraic K-theory, Advances in Soviet Mathematics, vol. 4 (American Mathematical Society, Providence, RI, 1991), 53–74.Google Scholar
Suslin, A., On the Grayson spectral sequence , Proc. Steklov Inst. Math. 241 (2003), 202–237.Google Scholar
Voevodsky, V., A1 -homotopy theory , inProceedings of International Congress of Mathematicians, Vol. 1 (Berlin, 1998), Doc. Math., 1998, Extra Vol. I, 579–604 (electronic).Google Scholar
Voevodsky, V., Open problems in the motivic stable homotopy theory I , in Motives, polylogarithms and Hodge theory I (International Press, Boston, MA, 2002), 3–34.Google Scholar
Voevodsky, V., A possible new approach to the motivic spectral sequence for algebraic K-theory , Contemp. Math. 293 (2002), 371–379.Google Scholar
Voevodsky, V., Reduced power operations in motivic cohomology , Publ. Math. Inst. Hautes Études Sci. 98 (2003), 1–57.Google Scholar
Voevodsky, V., Motivic Eilenberg–Mac Lane spaces , Publ. Math. Inst. Hautes Études Sci. 112 (2010), 1–99.Google Scholar
Voevodsky, V., Suslin, A. and Friedlander, E., Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000).Google Scholar
Weibel, Ch., The K-book: an introduction to algebraic K-theory, Graduate Studies in Mathematics, vol. 145 (American Mathematical Society, Providence, RI, 2013).Google Scholar