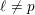Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T16:43:52.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimally ramified deformations when $\ell \neq p$

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  12 November 2018

Jeremy Booher
Jeremy Booher*
Affiliation:
Department of Mathematics, University of Arizona, Tucson, AZ 85721, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 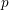$p$ and 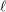$\ell$ be distinct primes, and let 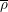$\overline{\unicode[STIX]{x1D70C}}$ be an orthogonal or symplectic representation of the absolute Galois group of an 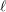$\ell$-adic field over a finite field of characteristic $p$. We define and study a liftable deformation condition of lifts of 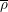$\overline{\unicode[STIX]{x1D70C}}$ ‘ramified no worse than 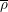$\overline{\unicode[STIX]{x1D70C}}$’, generalizing the minimally ramified deformation condition for 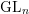$\operatorname{GL}_{n}$ studied in Clozel et al. [Automorphy for some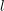$l$-adic lifts of automorphic mod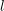$l$Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181; MR 2470687 (2010j:11082)]. The key insight is to restrict to deformations where an associated unipotent element does not change type when deforming. This requires an understanding of nilpotent orbits and centralizers of nilpotent elements in the relative situation, not just over fields.

Keywords

Galois representationsgeometric representationsdeformation theoryreductive groups

MSC classification

Primary: 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 1 , January 2019 , pp. 1 - 37
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Booher, J., Geometric deformations of orthogonal and symplectic Galois representations, PhD thesis, Stanford University (2016).Google Scholar
Booher, J., Producing geometric deformations of orthogonal and symplectic Galois representations , J. Number Theory 195 (2019), 115–158.Google Scholar
Borel, A. and Tits, J., Éléments unipotents et sous-groupes paraboliques de groupes réductifs. I , Invent. Math. 12 (1971), 95–104; MR 0294349 (45 #3419).Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181; MR 2470687 (2010j:11082).Google Scholar
Conrad, B., Reductive group schemes , in Autour des schémas en groupes. Vol. I, Panoramas et Synthèses vol. 42/43 (Société Mathématique de France, Paris, 2014), 93–444; MR 3362641.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive groups, New Mathematical Monographs, vol. 26, second edition (Cambridge University Press, Cambridge, 2015); MR 3362817.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III , Publ. Math. Inst. Hautes Études Sci. 28 (1966); MR 0217086.Google Scholar
Gan, W. T. and Yu, J.-K., Schémas en groupes et immeubles des groupes exceptionnels sur un corps local. I. Le groupe G 2 , Bull. Soc. Math. France 131 (2003), 307–358; MR 2017142 (2004j:14049).Google Scholar
Jantzen, J. C., Nilpotent orbits in representation theory , in Lie Theory, Progress in Mathematics, vol. 228 (Birkhäuser, Boston, MA, 2004), 1–211; MR 2042689 (2005c:14055).Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8, second edition (Cambridge University Press, Cambridge, 1989); MR 1011461.Google Scholar
Mazur, B., An introduction to the deformation theory of Galois representations , in Modular forms and Fermat’s last theorem (Boston, MA, 1995) (Springer, New York, 1997), 243–311; MR 1638481.Google Scholar
McNinch, G. J., The centralizer of a nilpotent section , Nagoya Math. J. 190 (2008), 129–181; MR 2423832 (2009d:20110).Google Scholar
Prasad, G. and Yu, J.-K., On quasi-reductive group schemes , J. Algebraic Geom. 15 (2006), 507–549; MR 2219847.Google Scholar
Ramakrishna, R., Lifting Galois representations , Invent. Math. 138 (1999), 537–562; MR 1719819 (2000j:11167).Google Scholar
Ramakrishna, R., Deforming Galois representations and the conjectures of Serre and Fontaine–Mazur , Ann. of Math. (2) 156 (2002), 115–154; MR 1935843 (2003k:11092).Google Scholar
The Sage Developers, Sagemath, the Sage Mathematics Software System (Version 6.7), 2015, http://www.sagemath.org.Google Scholar
Schlessinger, M., Functors of Artin rings , Trans. Amer. Math. Soc. 130 (1968), 208–222; MR 0217093.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42, translation of second French edition (Springer, New York–Heidelberg, 1977); MR 0450380 (56 #8675).Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental, Séminaire de Géométrie Algébrique du Bois Marie 1960–61 (SGA 1), Documents Mathématiques (Paris), vol. 3, updated and annotated reprint of [Lecture Notes in Mathematics, vol. 224 (Springer, Berlin, 1971); MR 0354651 (50 #7129)] (Société Mathématique de France, Paris, 2003); MR 2017446 (2004g:14017).Google Scholar
Demazure, M. and Grothendieck, A. (eds), Schémas en groupes III, Structure des schémas en groupes réductifs, Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3), Lecture Notes in Mathematics, vol. 153 (Springer, Berlin, 1970); MR 0274460.Google Scholar
Springer, T. A. and Steinberg, R., Conjugacy classes , in Seminar on algebraic groups and related finite groups, The Institute for Advanced Study, Princeton, NJ, 1968/69, Lecture Notes in Mathematics, vol. 131 (Springer, Berlin, 1970), 167–266; MR 0268192.Google Scholar
Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations. II , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239; MR 2470688 (2010j:11085).Google Scholar
Tilouine, J., Deformations of Galois representations and Hecke algebras (Mehta Research Institute of Mathematics and Mathematical Physics (Allahabad), Narosa Publishing House, New Delhi, 1996); MR 1643682.Google Scholar