Published online by Cambridge University Press: 14 August 2023
We single out a large class of groups 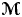 ${\rm {\boldsymbol {\mathscr {M}}}}$ for which the following unique prime factorization result holds: if
${\rm {\boldsymbol {\mathscr {M}}}}$ for which the following unique prime factorization result holds: if 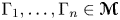 $\Gamma _1,\ldots,\Gamma _n\in {\rm {\boldsymbol {\mathscr {M}}}}$ and
$\Gamma _1,\ldots,\Gamma _n\in {\rm {\boldsymbol {\mathscr {M}}}}$ and  $\Gamma _1\times \cdots \times \Gamma _n$ is measure equivalent to a product
$\Gamma _1\times \cdots \times \Gamma _n$ is measure equivalent to a product  $\Lambda _1\times \cdots \times \Lambda _m$ of infinite icc groups, then
$\Lambda _1\times \cdots \times \Lambda _m$ of infinite icc groups, then 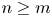 $n \ge m$, and if
$n \ge m$, and if  $n = m$, then, after permutation of the indices,
$n = m$, then, after permutation of the indices, 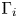 $\Gamma _i$ is measure equivalent to
$\Gamma _i$ is measure equivalent to 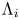 $\Lambda _i$, for all
$\Lambda _i$, for all 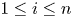 $1\leq i\leq n$. This provides an analogue of Monod and Shalom's theorem [Orbit equivalence rigidity and bounded cohomology, Ann. of Math. 164 (2006), 825–878] for groups that belong to
$1\leq i\leq n$. This provides an analogue of Monod and Shalom's theorem [Orbit equivalence rigidity and bounded cohomology, Ann. of Math. 164 (2006), 825–878] for groups that belong to 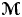 ${\rm {\boldsymbol {\mathscr {M}}}}$. Class
${\rm {\boldsymbol {\mathscr {M}}}}$. Class 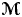 ${\rm {\boldsymbol {\mathscr {M}}}}$ is constructed using groups whose von Neumann algebras admit an s-malleable deformation in the sense of Sorin Popa and it contains all icc non-amenable groups
${\rm {\boldsymbol {\mathscr {M}}}}$ is constructed using groups whose von Neumann algebras admit an s-malleable deformation in the sense of Sorin Popa and it contains all icc non-amenable groups 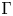 $\Gamma$ for which either (i)
$\Gamma$ for which either (i) 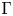 $\Gamma$ is an arbitrary wreath product group with amenable base or (ii)
$\Gamma$ is an arbitrary wreath product group with amenable base or (ii) 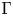 $\Gamma$ admits an unbounded 1-cocycle into its left regular representation. Consequently, we derive several orbit equivalence rigidity results for actions of product groups that belong to
$\Gamma$ admits an unbounded 1-cocycle into its left regular representation. Consequently, we derive several orbit equivalence rigidity results for actions of product groups that belong to 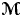 ${\rm {\boldsymbol {\mathscr {M}}}}$. Finally, for groups
${\rm {\boldsymbol {\mathscr {M}}}}$. Finally, for groups 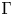 $\Gamma$ satisfying condition (ii), we show that all embeddings of group von Neumann algebras of non-amenable inner amenable groups into
$\Gamma$ satisfying condition (ii), we show that all embeddings of group von Neumann algebras of non-amenable inner amenable groups into 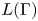 $L(\Gamma )$ are ‘rigid’. In particular, we provide an alternative solution to a question of Popa that was recently answered by Ding, Kunnawalkam Elayavalli, and Peterson [Properly Proximal von Neumann Algebras, Preprint (2022), arXiv:2204.00517].
$L(\Gamma )$ are ‘rigid’. In particular, we provide an alternative solution to a question of Popa that was recently answered by Ding, Kunnawalkam Elayavalli, and Peterson [Properly Proximal von Neumann Algebras, Preprint (2022), arXiv:2204.00517].
The author holds the postdoctoral fellowship fundamental research 12T5221N of the Research Foundation Flanders.