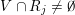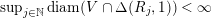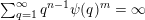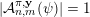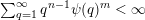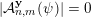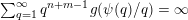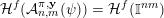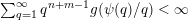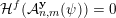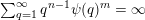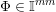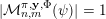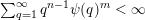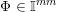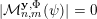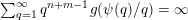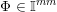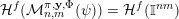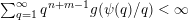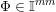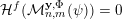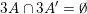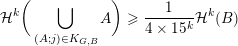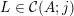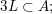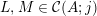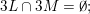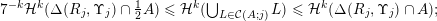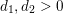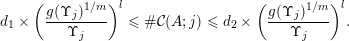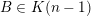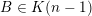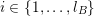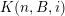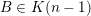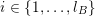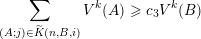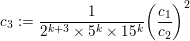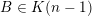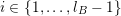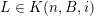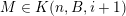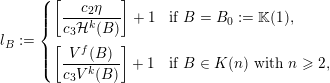1 Introduction
The main goal of this paper is to settle a problem posed in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] regarding the mass transference principle, a technique in geometric measure theory that was originally discovered in [Reference Beresnevich and VelaniBV06a] having primarily been motivated by applications in metric number theory. To some extent the present work is also driven by such applications.
To begin with, recall that the sets of interest in metric number theory often arise as the upper limit of a sequence of ‘elementary’ sets, such as balls, and satisfy elegant zero-one laws. Recall that if
![]() $(E_{i})_{i\in \mathbb{N}}$
is a sequence of sets then the upper limit or
$(E_{i})_{i\in \mathbb{N}}$
is a sequence of sets then the upper limit or
![]() $\limsup$
of this sequence is defined as
$\limsup$
of this sequence is defined as
 $$\begin{eqnarray}\displaystyle \limsup _{i\rightarrow \infty }E_{i}: & = & \displaystyle \{x:x\in E_{i}\text{ for infinitely many }i\in \mathbb{N}\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcap }_{n\in \mathbb{N}}\mathop{\bigcup }_{i\geqslant n}E_{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \limsup _{i\rightarrow \infty }E_{i}: & = & \displaystyle \{x:x\in E_{i}\text{ for infinitely many }i\in \mathbb{N}\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcap }_{n\in \mathbb{N}}\mathop{\bigcup }_{i\geqslant n}E_{i}.\nonumber\end{eqnarray}$$
These zero-one laws usually involve simple criteria, typically the convergence or divergence of a certain sum, for determining whether the measure of the
![]() $\limsup$
set is zero or one. To give an example, consider Khintchine’s classical theorem [Reference KhintchineKhi24] that deals with the set
$\limsup$
set is zero or one. To give an example, consider Khintchine’s classical theorem [Reference KhintchineKhi24] that deals with the set
![]() ${\mathcal{K}}(\unicode[STIX]{x1D713})$
of
${\mathcal{K}}(\unicode[STIX]{x1D713})$
of
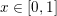 $x\in [0,1]$
such that
$x\in [0,1]$
such that
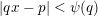 $$\begin{eqnarray}|qx-p|<\unicode[STIX]{x1D713}(q)\end{eqnarray}$$
$$\begin{eqnarray}|qx-p|<\unicode[STIX]{x1D713}(q)\end{eqnarray}$$
holds for infinitely many
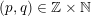 $(p,q)\in \mathbb{Z}\times \mathbb{N}$
. Clearly,
$(p,q)\in \mathbb{Z}\times \mathbb{N}$
. Clearly,
![]() ${\mathcal{K}}(\unicode[STIX]{x1D713})$
is the
${\mathcal{K}}(\unicode[STIX]{x1D713})$
is the
![]() $\limsup$
set of the intervals defined by (1), which are the ‘elementary’ sets in this setting. Khintchine proved that for any arithmetic function
$\limsup$
set of the intervals defined by (1), which are the ‘elementary’ sets in this setting. Khintchine proved that for any arithmetic function
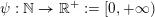 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}:=[0,+\infty )$
such that
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}:=[0,+\infty )$
such that
![]() $q\unicode[STIX]{x1D713}(q)$
is monotonic the Lebesgue measure of
$q\unicode[STIX]{x1D713}(q)$
is monotonic the Lebesgue measure of
![]() ${\mathcal{K}}(\unicode[STIX]{x1D713})$
is zero if
${\mathcal{K}}(\unicode[STIX]{x1D713})$
is zero if
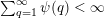 $\sum _{q=1}^{\infty }\unicode[STIX]{x1D713}(q)<\infty$
and one otherwise.
$\sum _{q=1}^{\infty }\unicode[STIX]{x1D713}(q)<\infty$
and one otherwise.
Around 1930, Jarník and Besicovitch both independently considered the size of
![]() ${\mathcal{K}}(\unicode[STIX]{x1D713})$
using Hausdorff measures and dimension, thus proving results enabling us to see the difference between sets
${\mathcal{K}}(\unicode[STIX]{x1D713})$
using Hausdorff measures and dimension, thus proving results enabling us to see the difference between sets
![]() ${\mathcal{K}}(\unicode[STIX]{x1D713})$
indistinguishable by Khintchine’s result. For example, the Jarník–Besicovitch theorem says that the Hausdorff dimension of
${\mathcal{K}}(\unicode[STIX]{x1D713})$
indistinguishable by Khintchine’s result. For example, the Jarník–Besicovitch theorem says that the Hausdorff dimension of
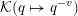 ${\mathcal{K}}(q\mapsto q^{-v})$
is
${\mathcal{K}}(q\mapsto q^{-v})$
is
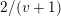 $2/(v+1)$
for
$2/(v+1)$
for
![]() $v>1$
.
$v>1$
.
Over time the findings of Khintchine, Jarník and Besicovitch have been sharpened and generalised in numerous ways, including to involve problems concerning systems of linear forms. The theories for the ambient measure and Hausdorff measures had been evolving relatively separately until the discovery of the so-called mass transference principle [Reference Beresnevich and VelaniBV06a]. This is a technique that enables one to easily obtain Hausdorff measure statements from a priori less general Lebesgue measure statements.
Let
![]() $f$
be a dimension function and let
$f$
be a dimension function and let
![]() ${\mathcal{H}}^{f}(\,\cdot \,)$
denote Hausdorff
${\mathcal{H}}^{f}(\,\cdot \,)$
denote Hausdorff
![]() $f$
-measure (see § 3.1 for definitions). Given a ball
$f$
-measure (see § 3.1 for definitions). Given a ball
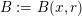 $B:=B(x,r)$
in
$B:=B(x,r)$
in
![]() $\mathbb{R}^{k}$
of radius
$\mathbb{R}^{k}$
of radius
![]() $r$
centred at
$r$
centred at
![]() $x$
, let
$x$
, let
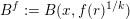 $B^{f}:=B(x,f(r)^{1/k})$
. When
$B^{f}:=B(x,f(r)^{1/k})$
. When
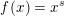 $f(x)=x^{s}$
for some
$f(x)=x^{s}$
for some
![]() $s>0$
we will denote
$s>0$
we will denote
![]() $B^{f}$
by
$B^{f}$
by
![]() $B^{s}$
. In particular, we always have that
$B^{s}$
. In particular, we always have that
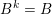 $B^{k}=B$
. The following statement is the main result of [Reference Beresnevich and VelaniBV06a].
$B^{k}=B$
. The following statement is the main result of [Reference Beresnevich and VelaniBV06a].
Mass transference principle. Let
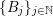 $\{B_{j}\}_{j\in \mathbb{N}}$
be a sequence of balls in
$\{B_{j}\}_{j\in \mathbb{N}}$
be a sequence of balls in
![]() $\mathbb{R}^{k}$
with
$\mathbb{R}^{k}$
with
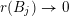 $r(B_{j})\rightarrow 0$
as
$r(B_{j})\rightarrow 0$
as
![]() $j\rightarrow \infty$
. Let
$j\rightarrow \infty$
. Let
![]() $f$
be a dimension function such that
$f$
be a dimension function such that
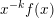 $x^{-k}f(x)$
is monotonic. Suppose that, for any ball
$x^{-k}f(x)$
is monotonic. Suppose that, for any ball
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{k}$
,
$\mathbb{R}^{k}$
,
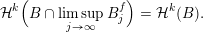 $$\begin{eqnarray}{\mathcal{H}}^{k}\Bigl(B\cap \limsup _{j\rightarrow \infty }B_{j}^{f}\Bigr)={\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\Bigl(B\cap \limsup _{j\rightarrow \infty }B_{j}^{f}\Bigr)={\mathcal{H}}^{k}(B).\end{eqnarray}$$
Then, for any ball
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{k}$
,
$\mathbb{R}^{k}$
,
 $$\begin{eqnarray}{\mathcal{H}}^{f}\Bigl(B\cap \limsup _{j\rightarrow \infty }B_{j}^{k}\Bigr)={\mathcal{H}}^{f}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}\Bigl(B\cap \limsup _{j\rightarrow \infty }B_{j}^{k}\Bigr)={\mathcal{H}}^{f}(B).\end{eqnarray}$$
The original mass transference principle [Reference Beresnevich and VelaniBV06a] stated above is a result regarding
![]() $\limsup$
sets which arise from sequences of balls. For the sake of completeness, we remark here that recently some progress has been made towards extending the mass transference principle to deal with
$\limsup$
sets which arise from sequences of balls. For the sake of completeness, we remark here that recently some progress has been made towards extending the mass transference principle to deal with
![]() $\limsup$
sets defined by sequences of rectangles [Reference Wang, Wu and XuWWX15]. In this paper, we will be dealing with the extension of the mass transference principle in the setting where we are interested in approximation by planes. This is not a new direction of research. Indeed, such an extension has already been obtained in [Reference Beresnevich and VelaniBV06b]. However, the mass transference principle result of [Reference Beresnevich and VelaniBV06b] carries some technical conditions which arise as a consequence of the ‘slicing’ technique that was used for the proof. These conditions were conjectured to be unnecessary and verifying that this is indeed the case is the main purpose of this paper.
$\limsup$
sets defined by sequences of rectangles [Reference Wang, Wu and XuWWX15]. In this paper, we will be dealing with the extension of the mass transference principle in the setting where we are interested in approximation by planes. This is not a new direction of research. Indeed, such an extension has already been obtained in [Reference Beresnevich and VelaniBV06b]. However, the mass transference principle result of [Reference Beresnevich and VelaniBV06b] carries some technical conditions which arise as a consequence of the ‘slicing’ technique that was used for the proof. These conditions were conjectured to be unnecessary and verifying that this is indeed the case is the main purpose of this paper.
Let
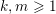 $k,m\geqslant 1$
and
$k,m\geqslant 1$
and
![]() $l\geqslant 0$
be integers such that
$l\geqslant 0$
be integers such that
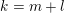 $k=m+l$
. Let
$k=m+l$
. Let
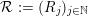 ${\mathcal{R}}:=(R_{j})_{j\in \mathbb{N}}$
be a family of planes in
${\mathcal{R}}:=(R_{j})_{j\in \mathbb{N}}$
be a family of planes in
![]() $\mathbb{R}^{k}$
of common dimension
$\mathbb{R}^{k}$
of common dimension
![]() $l$
. For every
$l$
. For every
![]() $j\in \mathbb{N}$
and
$j\in \mathbb{N}$
and
![]() $\unicode[STIX]{x1D6FF}\geqslant 0$
, define
$\unicode[STIX]{x1D6FF}\geqslant 0$
, define
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6FF}):=\{\mathbf{x}\in \mathbb{R}^{k}:\operatorname{dist}(\mathbf{x},R_{j})<\unicode[STIX]{x1D6FF}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6FF}):=\{\mathbf{x}\in \mathbb{R}^{k}:\operatorname{dist}(\mathbf{x},R_{j})<\unicode[STIX]{x1D6FF}\},\end{eqnarray}$$
where
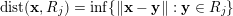 $\operatorname{dist}(\mathbf{x},R_{j})=\inf \{\Vert \mathbf{x}-\mathbf{y}\Vert :\mathbf{y}\in R_{j}\}$
and
$\operatorname{dist}(\mathbf{x},R_{j})=\inf \{\Vert \mathbf{x}-\mathbf{y}\Vert :\mathbf{y}\in R_{j}\}$
and
![]() $\Vert \cdot \Vert$
is any fixed norm on
$\Vert \cdot \Vert$
is any fixed norm on
![]() $\mathbb{R}^{k}$
.
$\mathbb{R}^{k}$
.
Let
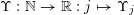 $\unicode[STIX]{x1D6F6}:\mathbb{N}\rightarrow \mathbb{R}:j\mapsto \unicode[STIX]{x1D6F6}_{j}$
be a non-negative real-valued function on
$\unicode[STIX]{x1D6F6}:\mathbb{N}\rightarrow \mathbb{R}:j\mapsto \unicode[STIX]{x1D6F6}_{j}$
be a non-negative real-valued function on
![]() $\mathbb{N}$
such that
$\mathbb{N}$
such that
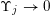 $\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
$\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
![]() $j\rightarrow \infty$
. Consider
$j\rightarrow \infty$
. Consider
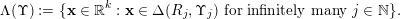 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}):=\{\mathbf{x}\in \mathbb{R}^{k}:\mathbf{x}\in \unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\text{ for infinitely many }j\in \mathbb{N}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}):=\{\mathbf{x}\in \mathbb{R}^{k}:\mathbf{x}\in \unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\text{ for infinitely many }j\in \mathbb{N}\}.\end{eqnarray}$$
In [Reference Beresnevich and VelaniBV06b], the following was established.
Theorem BV1. Let
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
![]() $\unicode[STIX]{x1D6F6}$
be as given above. Let
$\unicode[STIX]{x1D6F6}$
be as given above. Let
![]() $V$
be a linear subspace of
$V$
be a linear subspace of
![]() $\mathbb{R}^{k}$
such that
$\mathbb{R}^{k}$
such that
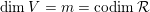 $\dim V=m=\text{codim}\,{\mathcal{R}}$
,
$\dim V=m=\text{codim}\,{\mathcal{R}}$
,
(i)
 $V\cap R_{j}\neq \emptyset$
for all
$V\cap R_{j}\neq \emptyset$
for all
 $j\in \mathbb{N}$
; and
$j\in \mathbb{N}$
; and(ii)
 $\sup _{j\in \mathbb{N}}\operatorname{diam}(V\cap \unicode[STIX]{x1D6E5}(R_{j},1))<\infty$
.
$\sup _{j\in \mathbb{N}}\operatorname{diam}(V\cap \unicode[STIX]{x1D6E5}(R_{j},1))<\infty$
.
Let
![]() $f$
and
$f$
and
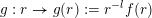 $g:r\rightarrow g(r):=r^{-l}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-l}f(r)$
be dimension functions such that
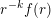 $r^{-k}f(r)$
is monotonic and let
$r^{-k}f(r)$
is monotonic and let
![]() $\unicode[STIX]{x1D6FA}$
be a ball in
$\unicode[STIX]{x1D6FA}$
be a ball in
![]() $\mathbb{R}^{k}$
. Suppose that, for any ball
$\mathbb{R}^{k}$
. Suppose that, for any ball
![]() $B$
in
$B$
in
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
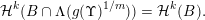 $$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B).\end{eqnarray}$$
Then, for any ball
![]() $B$
in
$B$
in
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
 $$\begin{eqnarray}{\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B).\end{eqnarray}$$
Remark.
In the case that
![]() $l=0$
and
$l=0$
and
![]() $\unicode[STIX]{x1D6FA}=\mathbb{R}^{k}$
, Theorem BV1 coincides with the mass transference principle stated above.
$\unicode[STIX]{x1D6FA}=\mathbb{R}^{k}$
, Theorem BV1 coincides with the mass transference principle stated above.
The conditions (i) and (ii) in Theorem BV1 arise as a consequence of the particular proof strategy employed in [Reference Beresnevich and VelaniBV06b]. However, it was conjectured [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09, Conjecture E] that Theorem BV1 should be true without conditions (i) and (ii). By adopting a different proof strategy (one similar to that used to prove the mass transference principle in [Reference Beresnevich and VelaniBV06a] rather than ‘slicing’) we are able to remove conditions (i) and (ii) and, consequently, prove the following.
Theorem 1. Let
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
![]() $\unicode[STIX]{x1D6F6}$
be as given above. Let
$\unicode[STIX]{x1D6F6}$
be as given above. Let
![]() $f$
and
$f$
and
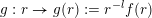 $g:r\rightarrow g(r):=r^{-l}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-l}f(r)$
be dimension functions such that
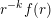 $r^{-k}f(r)$
is monotonic and let
$r^{-k}f(r)$
is monotonic and let
![]() $\unicode[STIX]{x1D6FA}$
be a ball in
$\unicode[STIX]{x1D6FA}$
be a ball in
![]() $\mathbb{R}^{k}$
. Suppose that, for any ball
$\mathbb{R}^{k}$
. Suppose that, for any ball
![]() $B$
in
$B$
in
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
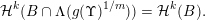 $$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B).\end{eqnarray}$$
Then, for any ball
![]() $B$
in
$B$
in
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
 $$\begin{eqnarray}{\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B).\end{eqnarray}$$
At first glance, conditions (i) and (ii) in Theorem BV1 do not seem particularly restrictive. Indeed, there are a number of interesting consequences of this theorem, see [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09, Reference Beresnevich and VelaniBV06b]. However, in the following section we present applications of Theorem 1 which may well be out of reach when using Theorem BV1. In § 3 and § 4 we establish necessary preliminaries and some auxiliary lemmas before presenting the full proof of Theorem 1 in § 5.
2 Some applications of Theorem 1
In this section we highlight merely a few applications of Theorem 1 which we hope give an idea of the breadth of its consequences. In § 2.1 we show that, using Theorem 1, with relative ease we are able to remove the last remaining monotonicity condition from a Hausdorff measure analogue of the classical Khintchine–Groshev theorem. We also show how the same outcome may be achieved, albeit with a somewhat longer proof, by using Theorem BV1 instead of Theorem 1. In § 2.2 we obtain a Hausdorff measure analogue of the inhomogeneous version of the Khintchine–Groshev theorem.
In § 2.3 we present Hausdorff measure analogues of some recent results of Dani, Laurent and Nogueira [Reference Dani, Laurent and NogueiraDLN15]. They have established Khintchine–Groshev type statements in which the approximating points
![]() $(\mathbf{p},\mathbf{q})$
are subject to certain primitivity conditions. We obtain the corresponding Hausdorff measure results. On the way to realising some of the results outlined above, in § 2.2 and § 2.3 we develop several more general statements which reformulate Theorem 1 in terms of transferring Lebesgue measure statements to Hausdorff measure statements for very general sets of
$(\mathbf{p},\mathbf{q})$
are subject to certain primitivity conditions. We obtain the corresponding Hausdorff measure results. On the way to realising some of the results outlined above, in § 2.2 and § 2.3 we develop several more general statements which reformulate Theorem 1 in terms of transferring Lebesgue measure statements to Hausdorff measure statements for very general sets of
![]() $\unicode[STIX]{x1D6F9}$
-approximable points (see Theorems 4, 5 and 6). The recurring theme throughout this section is that, given more-or-less any Khintchine–Groshev type statement, Theorem 1 can be used to establish the corresponding Hausdorff measure result.
$\unicode[STIX]{x1D6F9}$
-approximable points (see Theorems 4, 5 and 6). The recurring theme throughout this section is that, given more-or-less any Khintchine–Groshev type statement, Theorem 1 can be used to establish the corresponding Hausdorff measure result.
2.1 The Khintchine–Groshev theorem for Hausdorff measures
Let
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $m\geqslant 1$
be integers. Denote by
$m\geqslant 1$
be integers. Denote by
![]() $\mathbb{I}^{nm}$
the unit cube
$\mathbb{I}^{nm}$
the unit cube
![]() $[0,1]^{nm}$
in
$[0,1]^{nm}$
in
![]() $\mathbb{R}^{nm}$
. Throughout this section we consider
$\mathbb{R}^{nm}$
. Throughout this section we consider
![]() $\mathbb{R}^{nm}$
equipped with the norm
$\mathbb{R}^{nm}$
equipped with the norm
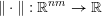 $\Vert \cdot \Vert :\mathbb{R}^{nm}\rightarrow \mathbb{R}$
defined as follows:
$\Vert \cdot \Vert :\mathbb{R}^{nm}\rightarrow \mathbb{R}$
defined as follows:
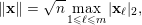 $$\begin{eqnarray}\Vert \mathbf{x}\Vert =\sqrt{n}\max _{1\leqslant \ell \leqslant m}|\mathbf{x}_{\ell }|_{2},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \mathbf{x}\Vert =\sqrt{n}\max _{1\leqslant \ell \leqslant m}|\mathbf{x}_{\ell }|_{2},\end{eqnarray}$$
where
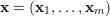 $\mathbf{x}=(\mathbf{x}_{1},\ldots ,\mathbf{x}_{m})$
with each
$\mathbf{x}=(\mathbf{x}_{1},\ldots ,\mathbf{x}_{m})$
with each
![]() $\mathbf{x}_{\ell }$
representing a column vector in
$\mathbf{x}_{\ell }$
representing a column vector in
![]() $\mathbb{R}^{n}$
for
$\mathbb{R}^{n}$
for
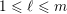 $1\leqslant \ell \leqslant m$
, and
$1\leqslant \ell \leqslant m$
, and
![]() $|\cdot |_{2}$
is the usual Euclidean norm on
$|\cdot |_{2}$
is the usual Euclidean norm on
![]() $\mathbb{R}^{n}$
. The role of the norm (3) will become apparent soon, namely through the proof of Theorem 2 below.
$\mathbb{R}^{n}$
. The role of the norm (3) will become apparent soon, namely through the proof of Theorem 2 below.
Given a function
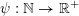 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
, let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
, let
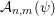 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
denote the set of
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
denote the set of
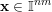 $\mathbf{x}\in \mathbb{I}^{nm}$
such that
$\mathbf{x}\in \mathbb{I}^{nm}$
such that
 $$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\end{eqnarray}$$
$$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\end{eqnarray}$$
for infinitely many
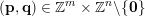 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Here,
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Here,
![]() $|\cdot |$
denotes the supremum norm,
$|\cdot |$
denotes the supremum norm,
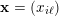 $\mathbf{x}=(x_{i\ell })$
is regarded as an
$\mathbf{x}=(x_{i\ell })$
is regarded as an
![]() $n\times m$
matrix and
$n\times m$
matrix and
![]() $\mathbf{q}$
and
$\mathbf{q}$
and
![]() $\mathbf{p}$
are regarded as a row vectors. Thus,
$\mathbf{p}$
are regarded as a row vectors. Thus,
![]() $\mathbf{q}\mathbf{x}$
represents a point in
$\mathbf{q}\mathbf{x}$
represents a point in
![]() $\mathbb{R}^{m}$
given by the system
$\mathbb{R}^{m}$
given by the system
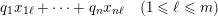 $$\begin{eqnarray}q_{1}x_{1\ell }+\cdots +q_{n}x_{n\ell }\quad (1\leqslant \ell \leqslant m)\end{eqnarray}$$
$$\begin{eqnarray}q_{1}x_{1\ell }+\cdots +q_{n}x_{n\ell }\quad (1\leqslant \ell \leqslant m)\end{eqnarray}$$
of
![]() $m$
real linear forms in
$m$
real linear forms in
![]() $n$
variables. We will say that the points in
$n$
variables. We will say that the points in
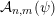 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
are
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
are
![]() $\unicode[STIX]{x1D713}$
-approximable. That
$\unicode[STIX]{x1D713}$
-approximable. That
 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
satisfies an elegant zero-one law in terms of
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
satisfies an elegant zero-one law in terms of
![]() $nm$
-dimensional Lebesgue measure when the function
$nm$
-dimensional Lebesgue measure when the function
![]() $\unicode[STIX]{x1D713}$
is monotonic is the content of the classical Khintchine–Groshev theorem. We opt to state here a modern version of this result which is best possible (see [Reference Beresnevich and VelaniBV10]).
$\unicode[STIX]{x1D713}$
is monotonic is the content of the classical Khintchine–Groshev theorem. We opt to state here a modern version of this result which is best possible (see [Reference Beresnevich and VelaniBV10]).
In what follows
![]() $|X|$
will denote the
$|X|$
will denote the
![]() $k$
-dimensional Lebesgue measure of
$k$
-dimensional Lebesgue measure of
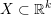 $X\subset \mathbb{R}^{k}$
.
$X\subset \mathbb{R}^{k}$
.
Theorem BV2. Let
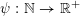 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function and let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function and let
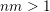 $nm>1$
. Then
$nm>1$
. Then
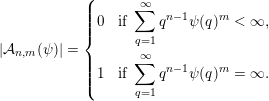 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}\displaystyle 0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ \displaystyle 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}\displaystyle 0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ \displaystyle 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
The earliest versions of this theorem were due to Khintchine and Groshev and included various extra constraints including monotonicity of
![]() $\unicode[STIX]{x1D713}$
. A famous counterexample constructed by Duffin and Schaeffer [Reference Duffin and SchaefferDS41] shows that, while Theorem BV2 also holds when
$\unicode[STIX]{x1D713}$
. A famous counterexample constructed by Duffin and Schaeffer [Reference Duffin and SchaefferDS41] shows that, while Theorem BV2 also holds when
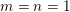 $m=n=1$
and
$m=n=1$
and
![]() $\unicode[STIX]{x1D713}$
is monotonic, the monotonicity condition cannot be removed when
$\unicode[STIX]{x1D713}$
is monotonic, the monotonicity condition cannot be removed when
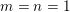 $m=n=1$
and so it is natural to exclude this situation by letting
$m=n=1$
and so it is natural to exclude this situation by letting
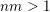 $nm>1$
. In the latter case, the monotonicity condition has been removed completely, leaving Theorem BV2. That monotonicity may be removed in the case
$nm>1$
. In the latter case, the monotonicity condition has been removed completely, leaving Theorem BV2. That monotonicity may be removed in the case
![]() $n=1$
is due to a result of Gallagher and in the case where
$n=1$
is due to a result of Gallagher and in the case where
![]() $n>2$
it is a consequence of a result due to Schmidt. For further details we refer the reader to [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] and references therein. The final unnecessary monotonicity condition to be removed was the
$n>2$
it is a consequence of a result due to Schmidt. For further details we refer the reader to [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] and references therein. The final unnecessary monotonicity condition to be removed was the
![]() $n=2$
case. Formally stated as Conjecture A in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09], this case was resolved in [Reference Beresnevich and VelaniBV10].
$n=2$
case. Formally stated as Conjecture A in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09], this case was resolved in [Reference Beresnevich and VelaniBV10].
Regarding the Hausdorff measure theory we shall show the following.
Theorem 2. Let
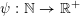 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be any approximating function and let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be any approximating function and let
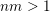 $nm>1$
. Let
$nm>1$
. Let
![]() $f$
and
$f$
and
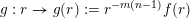 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
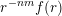 $r^{-nm}f(r)$
is monotonic. Then,
$r^{-nm}f(r)$
is monotonic. Then,
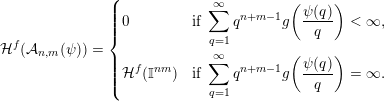 $$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}\displaystyle 0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ \displaystyle {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}\displaystyle 0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ \displaystyle {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
Theorem 2 is not entirely new and was in fact previously obtained in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] via Theorem BV1 subject to
![]() $\unicode[STIX]{x1D713}$
being monotonic in the case that
$\unicode[STIX]{x1D713}$
being monotonic in the case that
![]() $n=2$
. The deduction there was relying on a theorem of Sprindžuk rather than Theorem BV2 (which is what we shall use). In fact, with several additional assumptions imposed on
$n=2$
. The deduction there was relying on a theorem of Sprindžuk rather than Theorem BV2 (which is what we shall use). In fact, with several additional assumptions imposed on
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $f$
, the result was first obtained by Dickinson and Velani [Reference Dickinson and VelaniDV97]. Indeed, the proof of the convergence case of Theorem 2 makes use of standard covering arguments that, with little adjustment, can be drawn from [Reference Dickinson and VelaniDV97].
$f$
, the result was first obtained by Dickinson and Velani [Reference Dickinson and VelaniDV97]. Indeed, the proof of the convergence case of Theorem 2 makes use of standard covering arguments that, with little adjustment, can be drawn from [Reference Dickinson and VelaniDV97].
In what follows we shall give two proofs for the divergence case of Theorem 2, one using Theorem BV1 and the other using Theorem 1. The reason for this is to show the advantage of using Theorem 1 on the one hand, and to explicitly exhibit obstacles in using Theorem BV1 in other settings on the other hand. In the proofs we will use the following notation. For
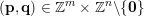 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
let
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
let
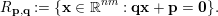 $$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}=\mathbf{0}\}.\end{eqnarray}$$
$$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}=\mathbf{0}\}.\end{eqnarray}$$
Note that, throughout the proofs of Theorem 2,
![]() $(\mathbf{p},\mathbf{q})$
will play the role of the index
$(\mathbf{p},\mathbf{q})$
will play the role of the index
![]() $j$
appearing in Theorem BV1 and Theorem 1. Also note that for
$j$
appearing in Theorem BV1 and Theorem 1. Also note that for
![]() $\unicode[STIX]{x1D6FF}\geqslant 0$
we have
$\unicode[STIX]{x1D6FF}\geqslant 0$
we have
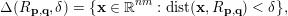 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6FF})=\{\mathbf{x}\in \mathbb{R}^{nm}:\operatorname{dist}(\mathbf{x},R_{\boldsymbol{ p},\mathbf{q}})<\unicode[STIX]{x1D6FF}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6FF})=\{\mathbf{x}\in \mathbb{R}^{nm}:\operatorname{dist}(\mathbf{x},R_{\boldsymbol{ p},\mathbf{q}})<\unicode[STIX]{x1D6FF}\},\end{eqnarray}$$
where
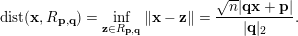 $$\begin{eqnarray}\operatorname{dist}(\mathbf{x},R_{\mathbf{p},\mathbf{q}})=\inf _{\mathbf{z}\in R_{\mathbf{p},\mathbf{q}}}\Vert \mathbf{x}-\mathbf{z}\Vert =\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{dist}(\mathbf{x},R_{\mathbf{p},\mathbf{q}})=\inf _{\mathbf{z}\in R_{\mathbf{p},\mathbf{q}}}\Vert \mathbf{x}-\mathbf{z}\Vert =\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}.\end{eqnarray}$$
We note that if
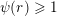 $\unicode[STIX]{x1D713}(r)\geqslant 1$
for infinitely many
$\unicode[STIX]{x1D713}(r)\geqslant 1$
for infinitely many
![]() $r\in \mathbb{N}$
, then
$r\in \mathbb{N}$
, then
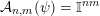 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})=\mathbb{I}^{nm}$
and the divergence case of Theorem 2 is trivial. Hence, without loss of generality we may assume that
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})=\mathbb{I}^{nm}$
and the divergence case of Theorem 2 is trivial. Hence, without loss of generality we may assume that
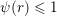 $\unicode[STIX]{x1D713}(r)\leqslant 1$
for all
$\unicode[STIX]{x1D713}(r)\leqslant 1$
for all
![]() $r\in \mathbb{N}$
. First we show how
$r\in \mathbb{N}$
. First we show how
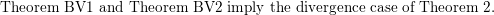 $$\begin{eqnarray}\text{Theorem BV1 and Theorem BV2 imply the divergence case of Theorem 2.}\end{eqnarray}$$
$$\begin{eqnarray}\text{Theorem BV1 and Theorem BV2 imply the divergence case of Theorem 2.}\end{eqnarray}$$
Proof. Recall that
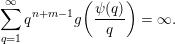 $$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
To use Theorem BV1 we have to restrict the approximating integer points
![]() $\mathbf{q}$
in order to meet conditions (i) and (ii) of Theorem BV1. We will use the same idea as in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09]; namely, we will impose the requirement that
$\mathbf{q}$
in order to meet conditions (i) and (ii) of Theorem BV1. We will use the same idea as in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09]; namely, we will impose the requirement that
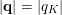 $|\mathbf{q}|=|q_{K}|$
for a fixed
$|\mathbf{q}|=|q_{K}|$
for a fixed
 $K\in \{1,\ldots ,n\}$
. Sprindžuk’s theorem that is used in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] allows for the introduction of this requirement almost instantly. Unfortunately, this is not the case when one is using Theorem BV2 and hence we will need a new argument. For each
$K\in \{1,\ldots ,n\}$
. Sprindžuk’s theorem that is used in [Reference Beresnevich, Bernik, Dodson and VelaniBBDV09] allows for the introduction of this requirement almost instantly. Unfortunately, this is not the case when one is using Theorem BV2 and hence we will need a new argument. For each
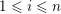 $1\leqslant i\leqslant n$
define the auxiliary functions
$1\leqslant i\leqslant n$
define the auxiliary functions
 $\unicode[STIX]{x1D6F9}_{i}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
by setting
$\unicode[STIX]{x1D6F9}_{i}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
by setting
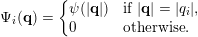 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D713}(|\mathbf{q}|) & \text{if }|\mathbf{q}|=|q_{i}|,\\ \displaystyle 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D713}(|\mathbf{q}|) & \text{if }|\mathbf{q}|=|q_{i}|,\\ \displaystyle 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
In what follows, similarly to
 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
, we consider sets
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
, we consider sets
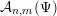 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9})$
of points
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9})$
of points
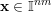 $\mathbf{x}\in \mathbb{I}^{nm}$
such that
$\mathbf{x}\in \mathbb{I}^{nm}$
such that
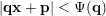 $$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6F9}(\mathbf{q})\end{eqnarray}$$
$$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6F9}(\mathbf{q})\end{eqnarray}$$
for infinitely many pairs
 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
, where
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
, where
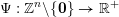 $\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
is a multivariable function. Since, by definition,
$\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
is a multivariable function. Since, by definition,
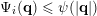 $\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})\leqslant \unicode[STIX]{x1D713}(|\mathbf{q}|)$
for each
$\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})\leqslant \unicode[STIX]{x1D713}(|\mathbf{q}|)$
for each
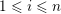 $1\leqslant i\leqslant n$
and each
$1\leqslant i\leqslant n$
and each
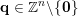 $\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
, it follows that
$\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
, it follows that
 $$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{i})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})\quad \text{for each }1\leqslant i\leqslant n.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{i})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})\quad \text{for each }1\leqslant i\leqslant n.\end{eqnarray}$$
By (6), to complete the proof of (4), it is sufficient to show that
 $$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{K}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})\quad \text{for some }1\leqslant K\leqslant n.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{K}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})\quad \text{for some }1\leqslant K\leqslant n.\end{eqnarray}$$
Without loss of generality we will assume that
![]() $K=1$
. Define
$K=1$
. Define
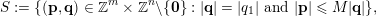 $$\begin{eqnarray}S:=\{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}:|\mathbf{q}|=|q_{1}|\text{and }|\mathbf{p}|\leqslant M|\mathbf{q}|\},\end{eqnarray}$$
$$\begin{eqnarray}S:=\{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}:|\mathbf{q}|=|q_{1}|\text{and }|\mathbf{p}|\leqslant M|\mathbf{q}|\},\end{eqnarray}$$
where
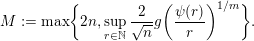 $$\begin{eqnarray}M:=\max \biggl\{2n,\sup _{r\in \mathbb{N}}\frac{2}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}M:=\max \biggl\{2n,\sup _{r\in \mathbb{N}}\frac{2}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\biggr\}.\end{eqnarray}$$
Note that, since
![]() $g$
is increasing and
$g$
is increasing and
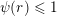 $\unicode[STIX]{x1D713}(r)\leqslant 1$
, the constant
$\unicode[STIX]{x1D713}(r)\leqslant 1$
, the constant
![]() $M$
is finite. Let
$M$
is finite. Let
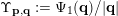 $\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}}:=\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})/|\mathbf{q}|$
for each
$\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}}:=\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})/|\mathbf{q}|$
for each
 $(\mathbf{p},\mathbf{q})\in S$
. The purpose for introducing this auxiliary set
$(\mathbf{p},\mathbf{q})\in S$
. The purpose for introducing this auxiliary set
![]() $S$
will become apparent later. Now, for each
$S$
will become apparent later. Now, for each
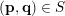 $(\mathbf{p},\mathbf{q})\in S$
,
$(\mathbf{p},\mathbf{q})\in S$
,
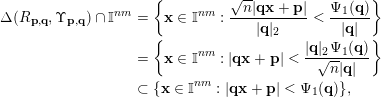 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{\sqrt{n}|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{\sqrt{n}|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})\},\nonumber\end{eqnarray}$$
since
 $|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. It follows that
$|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. It follows that
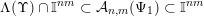 $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{1})\subset \mathbb{I}^{nm}$
, where
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6F9}_{1})\subset \mathbb{I}^{nm}$
, where
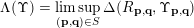 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})=\limsup _{(\mathbf{p},\mathbf{q})\in S}\unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})=\limsup _{(\mathbf{p},\mathbf{q})\in S}\unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\end{eqnarray}$$
and, in taking this limit,
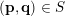 $(\mathbf{p},\mathbf{q})\in S$
can be arranged in any order. Therefore, (7) will follow on showing that
$(\mathbf{p},\mathbf{q})\in S$
can be arranged in any order. Therefore, (7) will follow on showing that
 $$\begin{eqnarray}{\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
Showing (9) will rely on Theorem BV1. First of all observe that conditions (i) and (ii) are met with the
![]() $m$
-dimensional subspace
$m$
-dimensional subspace
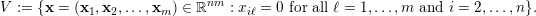 $$\begin{eqnarray}V:=\{\mathbf{x}=(\mathbf{x}_{1},\mathbf{x}_{2},\ldots ,\mathbf{x}_{m})\in \mathbb{R}^{nm}:x_{i\ell }=0\text{ for all }\ell =1,\ldots ,m\text{ and }i=2,\ldots ,n\}.\end{eqnarray}$$
$$\begin{eqnarray}V:=\{\mathbf{x}=(\mathbf{x}_{1},\mathbf{x}_{2},\ldots ,\mathbf{x}_{m})\in \mathbb{R}^{nm}:x_{i\ell }=0\text{ for all }\ell =1,\ldots ,m\text{ and }i=2,\ldots ,n\}.\end{eqnarray}$$
Indeed, regarding condition (i), we have that
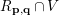 $R_{\mathbf{p},\mathbf{q}}\cap V$
consists of the single element
$R_{\mathbf{p},\mathbf{q}}\cap V$
consists of the single element
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}\displaystyle -\frac{p_{1}}{q_{1}} & \displaystyle -\frac{p_{2}}{q_{1}} & \ldots \, & \displaystyle -\frac{p_{m}}{q_{1}}\\ 0 & 0 & \ldots \, & 0\\ \vdots & \vdots & \cdots \, & \vdots \\ 0 & 0 & \ldots \, & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}\displaystyle -\frac{p_{1}}{q_{1}} & \displaystyle -\frac{p_{2}}{q_{1}} & \ldots \, & \displaystyle -\frac{p_{m}}{q_{1}}\\ 0 & 0 & \ldots \, & 0\\ \vdots & \vdots & \cdots \, & \vdots \\ 0 & 0 & \ldots \, & 0\end{array}\right),\end{eqnarray}$$
and so is non-empty. Regarding condition (ii), for
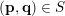 $(\mathbf{p},\mathbf{q})\in S$
we have that
$(\mathbf{p},\mathbf{q})\in S$
we have that
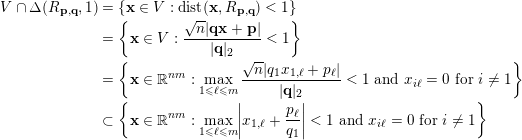 $$\begin{eqnarray}\displaystyle V\cap \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},1) & = & \displaystyle \{\mathbf{x}\in V:\operatorname{dist}(\mathbf{x},R_{\mathbf{p},\mathbf{q}})<1\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in V:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<1\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{R}^{nm}:\displaystyle \max _{1\leqslant \ell \leqslant m}\frac{\sqrt{n}|q_{1}x_{1,\ell }+p_{\ell }|}{|\mathbf{q}|_{2}}<1\text{ and }x_{i\ell }=0\text{ for }i\not =1\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{R}^{nm}:\displaystyle \max _{1\leqslant \ell \leqslant m}\biggl|x_{1,\ell }+\frac{p_{\ell }}{q_{1}}\biggr|<1\text{ and }x_{i\ell }=0\text{ for }i\not =1\biggr\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V\cap \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},1) & = & \displaystyle \{\mathbf{x}\in V:\operatorname{dist}(\mathbf{x},R_{\mathbf{p},\mathbf{q}})<1\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in V:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<1\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{R}^{nm}:\displaystyle \max _{1\leqslant \ell \leqslant m}\frac{\sqrt{n}|q_{1}x_{1,\ell }+p_{\ell }|}{|\mathbf{q}|_{2}}<1\text{ and }x_{i\ell }=0\text{ for }i\not =1\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{R}^{nm}:\displaystyle \max _{1\leqslant \ell \leqslant m}\biggl|x_{1,\ell }+\frac{p_{\ell }}{q_{1}}\biggr|<1\text{ and }x_{i\ell }=0\text{ for }i\not =1\biggr\}\nonumber\end{eqnarray}$$
since
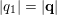 $|q_{1}|=|\mathbf{q}|$
and
$|q_{1}|=|\mathbf{q}|$
and
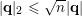 $|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Hence
$|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Hence
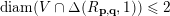 $\operatorname{diam}(V\cap \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},1))\leqslant 2$
and we are done.
$\operatorname{diam}(V\cap \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},1))\leqslant 2$
and we are done.
Now let
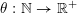 $\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be given by
$\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be given by
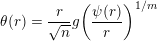 $$\begin{eqnarray}\unicode[STIX]{x1D703}(r)=\frac{r}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(r)=\frac{r}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\end{eqnarray}$$
and, for each
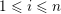 $1\leqslant i\leqslant n$
, let
$1\leqslant i\leqslant n$
, let
 $\unicode[STIX]{x1D6E9}_{i}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be given by
$\unicode[STIX]{x1D6E9}_{i}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be given by
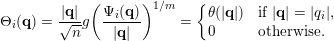 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})=\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D703}(|\mathbf{q}|)\quad & \text{if }|\mathbf{q}|=|q_{i}|,\\ \displaystyle 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})=\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{i}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D703}(|\mathbf{q}|)\quad & \text{if }|\mathbf{q}|=|q_{i}|,\\ \displaystyle 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Similarly to (6), we have that
 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})$
for each
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})$
for each
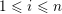 $1\leqslant i\leqslant n$
. Furthermore,
$1\leqslant i\leqslant n$
. Furthermore,
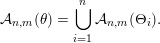 $$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})=\mathop{\bigcup }_{i=1}^{n}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})=\mathop{\bigcup }_{i=1}^{n}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i}).\end{eqnarray}$$
Indeed, the ‘
![]() $\supset$
’ inclusion follows from the above. To show the converse, note that for any
$\supset$
’ inclusion follows from the above. To show the converse, note that for any
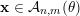 $\mathbf{x}\in {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})$
the inequality
$\mathbf{x}\in {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})$
the inequality
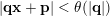 $|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)$
is satisfied for infinitely many
$|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)$
is satisfied for infinitely many
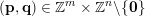 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Clearly, for each
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Clearly, for each
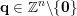 $\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
we have that
$\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
we have that
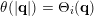 $\unicode[STIX]{x1D703}(|\mathbf{q}|)=\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})$
for some
$\unicode[STIX]{x1D703}(|\mathbf{q}|)=\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})$
for some
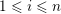 $1\leqslant i\leqslant n$
. Therefore, there is a fixed
$1\leqslant i\leqslant n$
. Therefore, there is a fixed
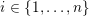 $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
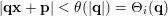 $|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)=\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})$
is satisfied for infinitely many
$|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)=\unicode[STIX]{x1D6E9}_{i}(\mathbf{q})$
is satisfied for infinitely many
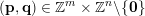 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. This means that
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. This means that
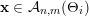 $\mathbf{x}\in {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i})$
for some
$\mathbf{x}\in {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{i})$
for some
![]() $i$
, thus verifying (10).
$i$
, thus verifying (10).
Next, observe that, by (5), the sum
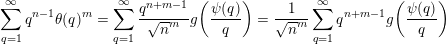 $$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }\frac{q^{n+m-1}}{\sqrt{n}^{m}}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\frac{1}{\sqrt{n}^{m}}\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }\frac{q^{n+m-1}}{\sqrt{n}^{m}}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\frac{1}{\sqrt{n}^{m}}\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)\end{eqnarray}$$
diverges. Therefore, by Theorem BV2, we have that
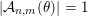 $|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})|=1$
. Hence, by (10), there exists some
$|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})|=1$
. Hence, by (10), there exists some
 $1\leqslant K\leqslant n$
such that
$1\leqslant K\leqslant n$
such that
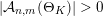 $|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|>0$
. By the zero-one law of [Reference Beresnevich and VelaniBV08, Theorem 1], we know that
$|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|>0$
. By the zero-one law of [Reference Beresnevich and VelaniBV08, Theorem 1], we know that
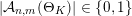 $|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|\in \{0,1\}$
. Hence,
$|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|\in \{0,1\}$
. Hence,
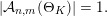 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|=1.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{K})|=1.\end{eqnarray}$$
Without loss of generality we will suppose that
![]() $K=1$
, the same as in (7).
$K=1$
, the same as in (7).
Now, using the fact that
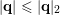 $|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
, for
$|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
, for
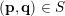 $(\mathbf{p},\mathbf{q})\in S$
we have that
$(\mathbf{p},\mathbf{q})\in S$
we have that
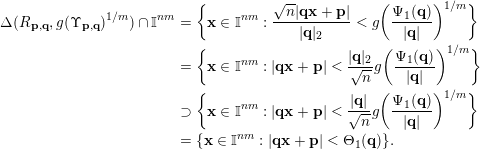 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6E9}_{1}(\mathbf{q})\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}_{1}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6E9}_{1}(\mathbf{q})\}.\nonumber\end{eqnarray}$$
Furthermore, observe that if
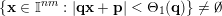 $\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6E9}_{1}(\mathbf{q})\}\not =\emptyset$
, then
$\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D6E9}_{1}(\mathbf{q})\}\not =\emptyset$
, then
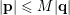 $|\mathbf{p}|\leqslant M|\mathbf{q}|$
and so
$|\mathbf{p}|\leqslant M|\mathbf{q}|$
and so
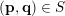 $(\mathbf{p},\mathbf{q})\in S$
. Therefore,
$(\mathbf{p},\mathbf{q})\in S$
. Therefore,
 $$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{1})\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}\subset \mathbb{I}^{nm}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D6E9}_{1})\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}\subset \mathbb{I}^{nm}.\end{eqnarray}$$
In particular,
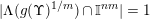 $|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\,\cap \,\mathbb{I}^{nm}|=1$
and so for any ball
$|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\,\cap \,\mathbb{I}^{nm}|=1$
and so for any ball
 $B\subset \mathbb{I}^{nm}$
we have that
$B\subset \mathbb{I}^{nm}$
we have that
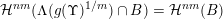 ${\mathcal{H}}^{nm}(\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap B)={\mathcal{H}}^{nm}(B)$
. Hence, we may apply Theorem BV1 with
${\mathcal{H}}^{nm}(\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap B)={\mathcal{H}}^{nm}(B)$
. Hence, we may apply Theorem BV1 with
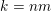 $k=nm$
,
$k=nm$
,
 $l=m(n-1)$
and
$l=m(n-1)$
and
![]() $m$
to conclude that, for any ball
$m$
to conclude that, for any ball
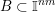 $B\subset \mathbb{I}^{nm}$
, we have
$B\subset \mathbb{I}^{nm}$
, we have
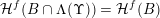 ${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular,
${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular,
 ${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
and the proof is thus complete.◻
${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
and the proof is thus complete.◻
We now show how
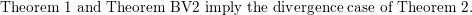 $$\begin{eqnarray}\text{Theorem 1 and Theorem BV2 imply the divergence case of Theorem 2.}\end{eqnarray}$$
$$\begin{eqnarray}\text{Theorem 1 and Theorem BV2 imply the divergence case of Theorem 2.}\end{eqnarray}$$
Proof. As before, we are given the divergence condition (5). For each pair
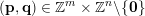 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
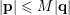 $|\mathbf{p}|\leqslant M|\mathbf{q}|$
, where
$|\mathbf{p}|\leqslant M|\mathbf{q}|$
, where
![]() $M$
is given by (8), let
$M$
is given by (8), let
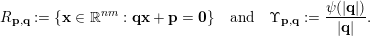 $$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}=\mathbf{0}\}\quad \text{and}\quad \unicode[STIX]{x1D6F6}_{\boldsymbol{ p},\mathbf{q}}:=\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}.\end{eqnarray}$$
$$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}=\mathbf{0}\}\quad \text{and}\quad \unicode[STIX]{x1D6F6}_{\boldsymbol{ p},\mathbf{q}}:=\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}.\end{eqnarray}$$
For such pairs
![]() $(\mathbf{p},\mathbf{q})$
we have that
$(\mathbf{p},\mathbf{q})$
we have that
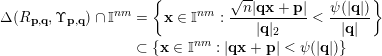 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\}\nonumber\end{eqnarray}$$
since
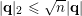 $|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Therefore
$|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Therefore
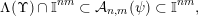 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})\subset \mathbb{I}^{nm},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})\subset \mathbb{I}^{nm},\end{eqnarray}$$
where the
![]() $\limsup$
is taken over
$\limsup$
is taken over
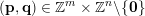 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
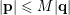 $|\mathbf{p}|\leqslant M|\mathbf{q}|$
.
$|\mathbf{p}|\leqslant M|\mathbf{q}|$
.
Consequently, if we could show that
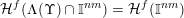 ${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
the divergence part of Theorem 2 would follow.
${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
the divergence part of Theorem 2 would follow.
Define
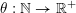 $\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
by
$\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
by
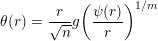 $$\begin{eqnarray}\unicode[STIX]{x1D703}(r)=\frac{r}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(r)=\frac{r}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}\end{eqnarray}$$
and note that
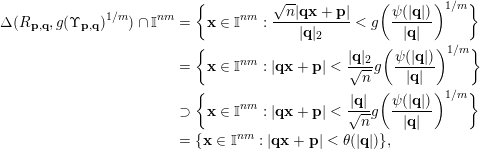 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D713}(|\mathbf{q}|)}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)\},\nonumber\end{eqnarray}$$
where this penultimate inclusion follows since
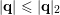 $|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
.
$|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
.
Observe that if
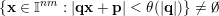 $\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)\}\not =\emptyset$
, then
$\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D703}(|\mathbf{q}|)\}\not =\emptyset$
, then
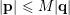 $|\mathbf{p}|\leqslant M|\mathbf{q}|$
. It follows that
$|\mathbf{p}|\leqslant M|\mathbf{q}|$
. It follows that
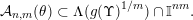 $$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}.\end{eqnarray}$$
Now, by Theorem BV2 and the divergence condition (5), we know that
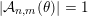 $|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})|=1$
since
$|{\mathcal{A}}_{n,m}(\unicode[STIX]{x1D703})|=1$
since
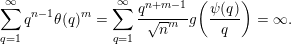 $$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }\frac{q^{n+m-1}}{\sqrt{n}^{m}}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }\frac{q^{n+m-1}}{\sqrt{n}^{m}}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
Hence,
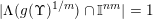 $|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}|=1$
and so we may apply Theorem 1 with
$|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}|=1$
and so we may apply Theorem 1 with
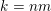 $k=nm$
,
$k=nm$
,
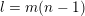 $l=m(n-1)$
and
$l=m(n-1)$
and
![]() $m$
to conclude that, for any ball
$m$
to conclude that, for any ball
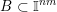 $B\subset \mathbb{I}^{nm}$
, we have
$B\subset \mathbb{I}^{nm}$
, we have
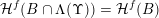 ${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular,
${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular,
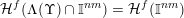 ${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
and so the proof is complete.◻
${\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
and so the proof is complete.◻
Remark 1. Note that the proof of (11) is not only shorter and simpler than that of (4) but it also does not rely on the zero-one law [Reference Beresnevich and VelaniBV08, Theorem 1]. This seemingly minor point becomes a substantial obstacle in trying to use the same line of argument as for (4) in other settings, for example, in inhomogeneous problems. The point is that, as of now, we do not have an inhomogeneous zero-one law similar to [Reference Beresnevich and VelaniBV08, Theorem 1], see [Reference RamírezRam17] for partial results and further comments. The approach based on using Theorem 1, on the other hand, works with ease in the inhomogeneous and other settings.
2.2 Inhomogeneous systems of linear forms
In this section we will be concerned with the inhomogeneous version of the Khintchine–Groshev theorem presented in the previous subsection. Given an approximating function
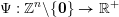 $\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
and a fixed
$\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
and a fixed
![]() $\mathbf{y}\in \mathbb{I}^{m}$
, we denote by
$\mathbf{y}\in \mathbb{I}^{m}$
, we denote by
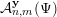 ${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})$
the set of
${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})$
the set of
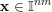 $\mathbf{x}\in \mathbb{I}^{nm}$
for which
$\mathbf{x}\in \mathbb{I}^{nm}$
for which
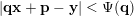 $$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{q})\end{eqnarray}$$
$$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{q})\end{eqnarray}$$
holds for infinitely many
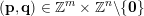 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. In the case that
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. In the case that
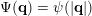 $\unicode[STIX]{x1D6F9}(\mathbf{q})=\unicode[STIX]{x1D713}(|\mathbf{q}|)$
for some function
$\unicode[STIX]{x1D6F9}(\mathbf{q})=\unicode[STIX]{x1D713}(|\mathbf{q}|)$
for some function
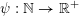 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
we write
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
we write
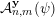 ${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})$
for
${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})$
for
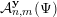 ${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})$
.
${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})$
.
Regarding inhomogeneous Diophantine approximation, we have the following statement which can be deduced as a corollary of [Reference SprindžukSpr79, ch. 1, Theorem 15]. In the case that
![]() $\unicode[STIX]{x1D713}$
is monotonic this statement also follows as a consequence of the ubiquity technique, see [Reference Beresnevich, Dickinson and VelaniBDV06, § 12.1].
$\unicode[STIX]{x1D713}$
is monotonic this statement also follows as a consequence of the ubiquity technique, see [Reference Beresnevich, Dickinson and VelaniBDV06, § 12.1].
Inhomogeneous Khintchine–Groshev theorem. Let
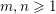 $m,n\geqslant 1$
be integers and let
$m,n\geqslant 1$
be integers and let
![]() $\mathbf{y}\in \mathbb{I}^{m}$
. If
$\mathbf{y}\in \mathbb{I}^{m}$
. If
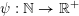 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
is an approximating function which is assumed to be monotonic if
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
is an approximating function which is assumed to be monotonic if
![]() $n=1$
or
$n=1$
or
![]() $n=2$
, then
$n=2$
, then
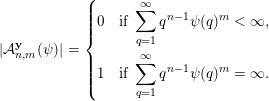 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
The following is the Hausdorff measure version of the above statement.
Theorem 3. Let
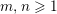 $m,n\geqslant 1$
be integers, let
$m,n\geqslant 1$
be integers, let
![]() $\mathbf{y}\in \mathbb{I}^{m}$
, and let
$\mathbf{y}\in \mathbb{I}^{m}$
, and let
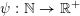 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
![]() $f$
and
$f$
and
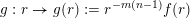 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
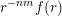 $r^{-nm}f(r)$
is monotonic. In the case that
$r^{-nm}f(r)$
is monotonic. In the case that
![]() $n=1$
or
$n=1$
or
![]() $n=2$
suppose also that
$n=2$
suppose also that
 $rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
is monotonic. Then,
$rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
is monotonic. Then,
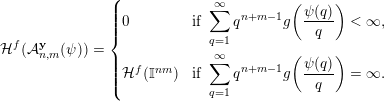 $$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
Remark 2. Although the condition that
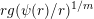 $rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
being monotonic when
$rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
being monotonic when
![]() $n=1$
or
$n=1$
or
![]() $n=2$
is the one that we naturally arrive at upon combining Theorem 1 with the inhomogeneous Khintchine–Groshev theorem, it is worth noting here that this condition may be relaxed. In the case when
$n=2$
is the one that we naturally arrive at upon combining Theorem 1 with the inhomogeneous Khintchine–Groshev theorem, it is worth noting here that this condition may be relaxed. In the case when
![]() $n=2$
, by appealing to the more general theorem of Sprindžuk [Reference SprindžukSpr79, ch. 1, Theorem 15] (from which the inhomogeneous Khintchine–Groshev theorem stated above can be deduced for
$n=2$
, by appealing to the more general theorem of Sprindžuk [Reference SprindžukSpr79, ch. 1, Theorem 15] (from which the inhomogeneous Khintchine–Groshev theorem stated above can be deduced for
![]() $n\geqslant 2$
), it is possible to replace monotonicity of
$n\geqslant 2$
), it is possible to replace monotonicity of
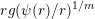 $rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
in the statement of Theorem 3 with the more aesthetically pleasing assumption that
$rg(\unicode[STIX]{x1D713}(r)/r)^{1/m}$
in the statement of Theorem 3 with the more aesthetically pleasing assumption that
![]() $\unicode[STIX]{x1D713}$
is monotonically decreasing. When
$\unicode[STIX]{x1D713}$
is monotonically decreasing. When
![]() $n=1$
it should be possible to make the same assumption replacement by using ideas from ubiquity (see [Reference Beresnevich, Dickinson and VelaniBDV06, § 12.1] and references within).
$n=1$
it should be possible to make the same assumption replacement by using ideas from ubiquity (see [Reference Beresnevich, Dickinson and VelaniBDV06, § 12.1] and references within).
The proof of the convergence case of Theorem 3 once again makes use of standard covering arguments. The divergence case is a consequence of the inhomogeneous Khintchine–Groshev theorem and Theorem 1. The proof of the divergence case is almost identical to that of (11) and we therefore leave the details out. Furthermore, exploiting this same argument a little further, we can use Theorem 1 to prove the following two more general statements from which both Theorems 2 and 3 follow as corollaries. In some sense Theorems 4 and 5 below are reformulations of Theorem 1 in terms of sets of
![]() $\unicode[STIX]{x1D6F9}$
-approximable (and
$\unicode[STIX]{x1D6F9}$
-approximable (and
![]() $\unicode[STIX]{x1D713}$
-approximable) points.
$\unicode[STIX]{x1D713}$
-approximable) points.
Theorem 4. Let
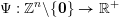 $\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be an approximating function and let
$\unicode[STIX]{x1D6F9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be an approximating function and let
![]() $\mathbf{y}\in \mathbb{I}^{m}$
. Let
$\mathbf{y}\in \mathbb{I}^{m}$
. Let
![]() $f$
and
$f$
and
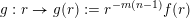 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
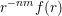 $r^{-nm}f(r)$
is monotonic. Let
$r^{-nm}f(r)$
is monotonic. Let
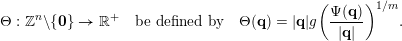 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D6E9}(\mathbf{q})=|\mathbf{q}|g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}:\mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D6E9}(\mathbf{q})=|\mathbf{q}|g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}.\end{eqnarray}$$
Then
 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6E9})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6E9})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
The following statement is a special case of Theorem 4 with
 $\unicode[STIX]{x1D6F9}(\mathbf{q}):=\unicode[STIX]{x1D713}(|\mathbf{q}|)$
.
$\unicode[STIX]{x1D6F9}(\mathbf{q}):=\unicode[STIX]{x1D713}(|\mathbf{q}|)$
.
Theorem 5. Let
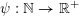 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function, let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function, let
![]() $\mathbf{y}\in \mathbb{I}^{m}$
and let
$\mathbf{y}\in \mathbb{I}^{m}$
and let
![]() $f$
and
$f$
and
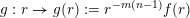 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
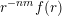 $r^{-nm}f(r)$
is monotonic. Let
$r^{-nm}f(r)$
is monotonic. Let
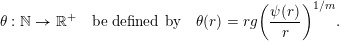 $$\begin{eqnarray}\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D703}(r)=rg\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D703}(r)=rg\biggl(\frac{\unicode[STIX]{x1D713}(r)}{r}\biggr)^{1/m}.\end{eqnarray}$$
Then
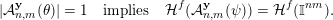 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D703})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D703})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
The proof of Theorem 4 is similar to that of (11). We shall explicitly deduce it from the even more general result of § 2.3, where the approximating function will be allowed to depend on
![]() $\mathbf{p}$
as well as
$\mathbf{p}$
as well as
![]() $\mathbf{q}$
. Theorem 3 now trivially follows on combining the inhomogeneous Khintchine–Groshev theorem with Theorem 5. Furthermore, any progress in removing the monotonicity constraint on
$\mathbf{q}$
. Theorem 3 now trivially follows on combining the inhomogeneous Khintchine–Groshev theorem with Theorem 5. Furthermore, any progress in removing the monotonicity constraint on
![]() $\unicode[STIX]{x1D713}$
from the inhomogeneous Khintchine–Groshev theorem can be instantly transferred into a Hausdorff measure statement upon applying Theorem 5. Indeed, we suspect that a full inhomogeneous analogue of Theorem BV2 must be true. Recall that it is open only in the case when
$\unicode[STIX]{x1D713}$
from the inhomogeneous Khintchine–Groshev theorem can be instantly transferred into a Hausdorff measure statement upon applying Theorem 5. Indeed, we suspect that a full inhomogeneous analogue of Theorem BV2 must be true. Recall that it is open only in the case when
![]() $n=1$
or
$n=1$
or
![]() $n=2$
.
$n=2$
.
2.3 Approximation by primitive points and more
The key goal of this section is to present Hausdorff measure analogues of some recent results obtained by Dani, Laurent and Nogueira in [Reference Dani, Laurent and NogueiraDLN15]. The setup they consider assumes certain coprimality conditions on the
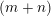 $(m+n)$
-tuple
$(m+n)$
-tuple
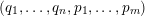 $(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})$
of approximating integers. To achieve our goal we will first prove a very general statement which further extends Theorems 4 and 5 and is of independent interest. In particular, we will allow for the approximating function to depend on
$(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})$
of approximating integers. To achieve our goal we will first prove a very general statement which further extends Theorems 4 and 5 and is of independent interest. In particular, we will allow for the approximating function to depend on
![]() $(\mathbf{p},\mathbf{q})$
and will also introduce a ‘distortion’ parameter
$(\mathbf{p},\mathbf{q})$
and will also introduce a ‘distortion’ parameter
![]() $\unicode[STIX]{x1D6F7}$
that allows certain flexibility within our framework. This allows us, for example, to incorporate the so-called ‘absolute value theory’ [Reference DickinsonDic93, Reference Hussain and KristensenHK13, Reference Hussain and LevesleyHL13].
$\unicode[STIX]{x1D6F7}$
that allows certain flexibility within our framework. This allows us, for example, to incorporate the so-called ‘absolute value theory’ [Reference DickinsonDic93, Reference Hussain and KristensenHK13, Reference Hussain and LevesleyHL13].
Within this section
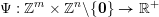 $\unicode[STIX]{x1D6F9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
will be a function of
$\unicode[STIX]{x1D6F9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
will be a function of
![]() $(\mathbf{p},\mathbf{q})$
,
$(\mathbf{p},\mathbf{q})$
,
![]() $\mathbf{y}\in \mathbb{I}^{m}$
will be a fixed point and
$\mathbf{y}\in \mathbb{I}^{m}$
will be a fixed point and
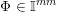 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
will be a fixed
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
will be a fixed
![]() $m\times m$
square matrix. Further, define
$m\times m$
square matrix. Further, define
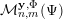 ${\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9})$
to be the set of
${\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9})$
to be the set of
 $\mathbf{x}\in \mathbb{I}^{nm}$
such that
$\mathbf{x}\in \mathbb{I}^{nm}$
such that
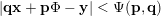 $$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})\end{eqnarray}$$
$$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})\end{eqnarray}$$
holds for
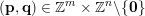 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
![]() $|\mathbf{q}|$
. Based upon Theorem 1, we now state and prove the following generalisation of Theorems 4 and 5.
$|\mathbf{q}|$
. Based upon Theorem 1, we now state and prove the following generalisation of Theorems 4 and 5.
Theorem 6. Let
 $\unicode[STIX]{x1D6F9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be such that
$\unicode[STIX]{x1D6F9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}$
be such that
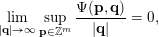 $$\begin{eqnarray}\displaystyle \lim _{|\mathbf{q}|\rightarrow \infty }\sup _{\mathbf{p}\in \mathbb{Z}^{m}}\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|\mathbf{q}|\rightarrow \infty }\sup _{\mathbf{p}\in \mathbb{Z}^{m}}\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}=0, & & \displaystyle\end{eqnarray}$$
and let
![]() $\mathbf{y}\in \mathbb{I}^{m}$
and
$\mathbf{y}\in \mathbb{I}^{m}$
and
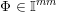 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
be fixed. Let
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
be fixed. Let
![]() $f$
and
$f$
and
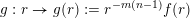 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
 $r^{-nm}f(r)$
is monotonic. Let
$r^{-nm}f(r)$
is monotonic. Let
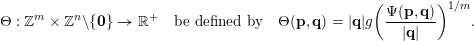 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})=|\mathbf{q}|g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}:\mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}\rightarrow \mathbb{R}^{+}\quad \text{be defined by}\quad \unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})=|\mathbf{q}|g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}.\end{eqnarray}$$
Then
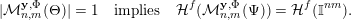 $$\begin{eqnarray}|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6E9})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6E9})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
Proof. Let
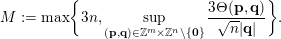 $$\begin{eqnarray}M:=\max \biggl\{3n,\sup _{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}}\frac{3\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})}{\sqrt{n}|\mathbf{q}|}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}M:=\max \biggl\{3n,\sup _{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}}\frac{3\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})}{\sqrt{n}|\mathbf{q}|}\biggr\}.\end{eqnarray}$$
By the monotonicity of
![]() $g$
and condition (12), we have that
$g$
and condition (12), we have that
![]() $M$
is finite. Let
$M$
is finite. Let
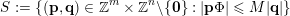 $$\begin{eqnarray}S:=\{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}:|\mathbf{p}\unicode[STIX]{x1D6F7}|\leqslant M|\mathbf{q}|\}\end{eqnarray}$$
$$\begin{eqnarray}S:=\{(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}:|\mathbf{p}\unicode[STIX]{x1D6F7}|\leqslant M|\mathbf{q}|\}\end{eqnarray}$$
and let
![]() $S_{\unicode[STIX]{x1D6F7}}$
be any fixed subset of
$S_{\unicode[STIX]{x1D6F7}}$
be any fixed subset of
![]() $S$
such that for each
$S$
such that for each
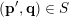 $(\mathbf{p}^{\prime },\mathbf{q})\in S$
there exists
$(\mathbf{p}^{\prime },\mathbf{q})\in S$
there exists
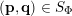 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
such that
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
such that
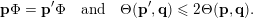 $$\begin{eqnarray}\mathbf{p}\unicode[STIX]{x1D6F7}=\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}\quad \text{and}\quad \unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\leqslant 2\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{p}\unicode[STIX]{x1D6F7}=\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}\quad \text{and}\quad \unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\leqslant 2\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q}).\end{eqnarray}$$
Furthermore, let
![]() $S_{\unicode[STIX]{x1D6F7}}$
be such that for all
$S_{\unicode[STIX]{x1D6F7}}$
be such that for all
 $(\mathbf{p},\mathbf{q}),(\mathbf{r},\mathbf{s})\in S_{\unicode[STIX]{x1D6F7}}$
we have
$(\mathbf{p},\mathbf{q}),(\mathbf{r},\mathbf{s})\in S_{\unicode[STIX]{x1D6F7}}$
we have
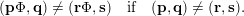 $$\begin{eqnarray}(\mathbf{p}\unicode[STIX]{x1D6F7},\mathbf{q})\neq (\mathbf{r}\unicode[STIX]{x1D6F7},\mathbf{s})\quad \text{if}\quad (\mathbf{p},\mathbf{q})\neq (\mathbf{r},\mathbf{s}).\end{eqnarray}$$
$$\begin{eqnarray}(\mathbf{p}\unicode[STIX]{x1D6F7},\mathbf{q})\neq (\mathbf{r}\unicode[STIX]{x1D6F7},\mathbf{s})\quad \text{if}\quad (\mathbf{p},\mathbf{q})\neq (\mathbf{r},\mathbf{s}).\end{eqnarray}$$
The existence of
![]() $S_{\unicode[STIX]{x1D6F7}}$
is easily seen. For each
$S_{\unicode[STIX]{x1D6F7}}$
is easily seen. For each
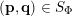 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
, let
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
, let
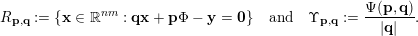 $$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}=\mathbf{0}\}\quad \text{and}\quad \unicode[STIX]{x1D6F6}_{\boldsymbol{ p},\mathbf{q}}:=\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}.\end{eqnarray}$$
$$\begin{eqnarray}R_{\mathbf{p},\mathbf{q}}:=\{\mathbf{x}\in \mathbb{R}^{nm}:\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}=\mathbf{0}\}\quad \text{and}\quad \unicode[STIX]{x1D6F6}_{\boldsymbol{ p},\mathbf{q}}:=\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}.\end{eqnarray}$$
For
 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
we have that
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
we have that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|}{|\mathbf{q}|_{2}}<\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr\}\nonumber\\ \displaystyle & \subset & \displaystyle \{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})\}\nonumber\end{eqnarray}$$
since
 $|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Also note that for each
$|\mathbf{q}|_{2}\leqslant \sqrt{n}|\mathbf{q}|$
. Also note that for each
 $\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
there are only finitely many
$\mathbf{q}\in \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
there are only finitely many
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
such that
$\mathbf{p}\in \mathbb{Z}^{m}$
such that
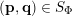 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Therefore
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Therefore
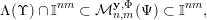 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9})\subset \mathbb{I}^{nm},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm}\subset {\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6F9})\subset \mathbb{I}^{nm},\end{eqnarray}$$
where, when defining
![]() $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
, the
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
, the
![]() $\limsup$
is taken over
$\limsup$
is taken over
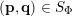 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Hence, by (14), it would suffice for us to show that
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Hence, by (14), it would suffice for us to show that
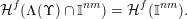 $$\begin{eqnarray}{\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\cap \mathbb{I}^{nm})={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
Consider
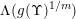 $\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})$
, where the
$\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})$
, where the
![]() $\limsup$
is again taken over
$\limsup$
is again taken over
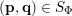 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Take any
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
. Take any
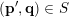 $(\mathbf{p}^{\prime },\mathbf{q})\in S$
and let
$(\mathbf{p}^{\prime },\mathbf{q})\in S$
and let
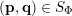 $(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
satisfy (13). Then, since
$(\mathbf{p},\mathbf{q})\in S_{\unicode[STIX]{x1D6F7}}$
satisfy (13). Then, since
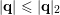 $|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
, we have that
$|\mathbf{q}|\leqslant |\mathbf{q}|_{2}$
, we have that
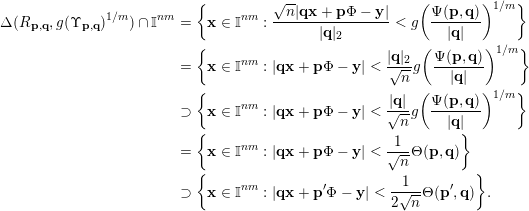 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}(R_{\mathbf{p},\mathbf{q}},g(\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}})^{1/m})\cap \mathbb{I}^{nm} & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:\frac{\sqrt{n}|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|}{|\mathbf{q}|_{2}}<g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{|\mathbf{q}|_{2}}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{|\mathbf{q}|}{\sqrt{n}}g\biggl(\frac{\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q})}{|\mathbf{q}|}\biggr)^{1/m}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q})\biggr\}\nonumber\\ \displaystyle & \supset & \displaystyle \biggl\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\biggr\}.\nonumber\end{eqnarray}$$
Also observe that if
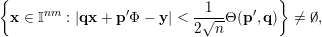 $$\begin{eqnarray}\bigg\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\bigg\}\not =\emptyset ,\end{eqnarray}$$
$$\begin{eqnarray}\bigg\{\mathbf{x}\in \mathbb{I}^{nm}:|\mathbf{q}\mathbf{x}+\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}-\mathbf{y}|<\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}(\mathbf{p}^{\prime },\mathbf{q})\bigg\}\not =\emptyset ,\end{eqnarray}$$
then
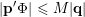 $|\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}|\leqslant M|\mathbf{q}|$
. It follows that
$|\mathbf{p}^{\prime }\unicode[STIX]{x1D6F7}|\leqslant M|\mathbf{q}|$
. It follows that
 $$\begin{eqnarray}{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}\biggl(\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}\biggr)\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\subset \mathbb{I}^{nm}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}\biggl(\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}\biggr)\subset \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\subset \mathbb{I}^{nm}.\end{eqnarray}$$
Recall that
 $|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6E9})|=1$
. Furthermore, in view of [Reference Beresnevich and VelaniBV08, Lemma 4], we have that
$|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6E9})|=1$
. Furthermore, in view of [Reference Beresnevich and VelaniBV08, Lemma 4], we have that
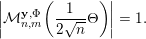 $$\begin{eqnarray}\bigg|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}\bigg(\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}\bigg)\bigg|=1.\end{eqnarray}$$
$$\begin{eqnarray}\bigg|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}\bigg(\frac{1}{2\sqrt{n}}\unicode[STIX]{x1D6E9}\bigg)\bigg|=1.\end{eqnarray}$$
Together with (15) this implies that
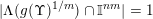 $|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}|=1$
. Further, note that, by (12),
$|\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})\cap \mathbb{I}^{nm}|=1$
. Further, note that, by (12),
 $\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}}\rightarrow 0$
as
$\unicode[STIX]{x1D6F6}_{\mathbf{p},\mathbf{q}}\rightarrow 0$
as
 $|\mathbf{q}|\rightarrow \infty$
. Therefore, Theorem 1 is applicable with
$|\mathbf{q}|\rightarrow \infty$
. Therefore, Theorem 1 is applicable with
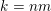 $k=nm$
,
$k=nm$
,
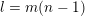 $l=m(n-1)$
and
$l=m(n-1)$
and
![]() $m$
and we conclude that for any ball
$m$
and we conclude that for any ball
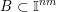 $B\subset \mathbb{I}^{nm}$
we have that
$B\subset \mathbb{I}^{nm}$
we have that
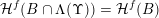 ${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular, this means that
${\mathcal{H}}^{f}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(B)$
. In particular, this means that
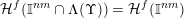 ${\mathcal{H}}^{f}(\mathbb{I}^{nm}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
, as required.◻
${\mathcal{H}}^{f}(\mathbb{I}^{nm}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
, as required.◻
Proof of Theorem 4.
Let
![]() $\unicode[STIX]{x1D6F9}$
be as in Theorem 4. First observe that if
$\unicode[STIX]{x1D6F9}$
be as in Theorem 4. First observe that if
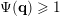 $\unicode[STIX]{x1D6F9}(\mathbf{q})\geqslant 1$
for infinitely many
$\unicode[STIX]{x1D6F9}(\mathbf{q})\geqslant 1$
for infinitely many
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
, then
$\mathbf{q}\in \mathbb{Z}^{n}$
, then
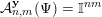 ${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})=\mathbb{I}^{nm}$
and there is nothing to prove. Otherwise we obviously have that
${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D6F9})=\mathbb{I}^{nm}$
and there is nothing to prove. Otherwise we obviously have that
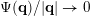 $\unicode[STIX]{x1D6F9}(\mathbf{q})/|\mathbf{q}|\rightarrow 0$
as
$\unicode[STIX]{x1D6F9}(\mathbf{q})/|\mathbf{q}|\rightarrow 0$
as
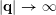 $|\mathbf{q}|\rightarrow \infty$
. In this case, extending
$|\mathbf{q}|\rightarrow \infty$
. In this case, extending
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6E9}$
to be functions of
$\unicode[STIX]{x1D6E9}$
to be functions of
![]() $(\mathbf{p},\mathbf{q})$
so that
$(\mathbf{p},\mathbf{q})$
so that
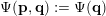 $\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q}):=\unicode[STIX]{x1D6F9}(\mathbf{q})$
and
$\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q}):=\unicode[STIX]{x1D6F9}(\mathbf{q})$
and
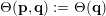 $\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q}):=\unicode[STIX]{x1D6E9}(\mathbf{q})$
, we immediately recover Theorem 4 from Theorem 6.◻
$\unicode[STIX]{x1D6E9}(\mathbf{p},\mathbf{q}):=\unicode[STIX]{x1D6E9}(\mathbf{q})$
, we immediately recover Theorem 4 from Theorem 6.◻
Theorem 6 can be applied in various situations beyond what has already been discussed above. For example, divergence results of [Reference Dickinson and HussainDH13] can be obtained by using Theorem 6 with
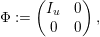 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:=\left(\begin{array}{@{}cc@{}}I_{u} & 0\\ 0 & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:=\left(\begin{array}{@{}cc@{}}I_{u} & 0\\ 0 & 0\end{array}\right),\end{eqnarray}$$
where
![]() $I_{u}$
is the identity matrix. In what follows we shall give applications of Theorem 6 in which the dependence of
$I_{u}$
is the identity matrix. In what follows we shall give applications of Theorem 6 in which the dependence of
![]() $\unicode[STIX]{x1D6F9}$
on both
$\unicode[STIX]{x1D6F9}$
on both
![]() $\mathbf{p}$
and
$\mathbf{p}$
and
![]() $\mathbf{q}$
becomes particularly useful. Namely, we shall extend the results of Dani, Laurent and Nogueira [Reference Dani, Laurent and NogueiraDLN15] to Hausdorff measures.
$\mathbf{q}$
becomes particularly useful. Namely, we shall extend the results of Dani, Laurent and Nogueira [Reference Dani, Laurent and NogueiraDLN15] to Hausdorff measures.
First we establish some notation. For any
![]() $d\geqslant 2$
let
$d\geqslant 2$
let
![]() $P(\mathbb{Z}^{d})$
be the set of points
$P(\mathbb{Z}^{d})$
be the set of points
 $\mathbf{v}=(v_{1},\ldots ,v_{d})\in \mathbb{Z}^{d}$
such that
$\mathbf{v}=(v_{1},\ldots ,v_{d})\in \mathbb{Z}^{d}$
such that
 $\gcd (v_{1},\ldots ,v_{d})=1$
. For any subset
$\gcd (v_{1},\ldots ,v_{d})=1$
. For any subset
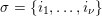 $\unicode[STIX]{x1D70E}=\{i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}\}$
of
$\unicode[STIX]{x1D70E}=\{i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}\}$
of
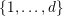 $\{1,\ldots ,d\}$
with
$\{1,\ldots ,d\}$
with
![]() $\unicode[STIX]{x1D708}\geqslant 2$
, let
$\unicode[STIX]{x1D708}\geqslant 2$
, let
![]() $P(\unicode[STIX]{x1D70E})$
be the set of points
$P(\unicode[STIX]{x1D70E})$
be the set of points
![]() $\mathbf{v}\in \mathbb{Z}^{d}$
such that
$\mathbf{v}\in \mathbb{Z}^{d}$
such that
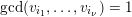 $\gcd (v_{i_{1}},\ldots ,v_{i_{\unicode[STIX]{x1D708}}})=1$
. Next, given a partition
$\gcd (v_{i_{1}},\ldots ,v_{i_{\unicode[STIX]{x1D708}}})=1$
. Next, given a partition
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
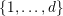 $\{1,\ldots ,d\}$
into disjoint subsets
$\{1,\ldots ,d\}$
into disjoint subsets
![]() $\unicode[STIX]{x1D70B}_{\ell }$
of at least two elements, let
$\unicode[STIX]{x1D70B}_{\ell }$
of at least two elements, let
![]() $P(\unicode[STIX]{x1D70B})$
be the set of points
$P(\unicode[STIX]{x1D70B})$
be the set of points
![]() $\mathbf{v}\in \mathbb{Z}^{d}$
such that
$\mathbf{v}\in \mathbb{Z}^{d}$
such that
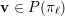 $\mathbf{v}\in P(\unicode[STIX]{x1D70B}_{\ell })$
for all components
$\mathbf{v}\in P(\unicode[STIX]{x1D70B}_{\ell })$
for all components
![]() $\unicode[STIX]{x1D70B}_{\ell }$
of
$\unicode[STIX]{x1D70B}_{\ell }$
of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Given an approximating function
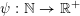 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
and fixed
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
and fixed
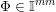 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
and
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
and
![]() $\mathbf{y}\in \mathbb{I}^{m}$
, let
$\mathbf{y}\in \mathbb{I}^{m}$
, let
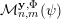 ${\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
be the set of
${\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
be the set of
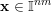 $\mathbf{x}\in \mathbb{I}^{nm}$
such that
$\mathbf{x}\in \mathbb{I}^{nm}$
such that
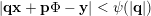 $$\begin{eqnarray}\displaystyle |\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D713}(|\mathbf{q}|) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathbf{q}\mathbf{x}+\mathbf{p}\unicode[STIX]{x1D6F7}-\mathbf{y}|<\unicode[STIX]{x1D713}(|\mathbf{q}|) & & \displaystyle\end{eqnarray}$$
holds for
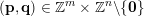 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
![]() $|\mathbf{q}|$
. Also, given a partition
$|\mathbf{q}|$
. Also, given a partition
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
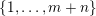 $\{1,\ldots ,m+n\}$
, let
$\{1,\ldots ,m+n\}$
, let
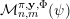 ${\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
denote the set of
${\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
denote the set of
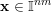 $\mathbf{x}\in \mathbb{I}^{nm}$
for which (16) is satisfied for
$\mathbf{x}\in \mathbb{I}^{nm}$
for which (16) is satisfied for
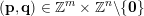 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
![]() $|\mathbf{q}|$
and with
$|\mathbf{q}|$
and with
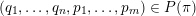 $(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
. Now specialising Theorem 6 for the approximating function
$(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
. Now specialising Theorem 6 for the approximating function
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q}):=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D713}(|\mathbf{q}|) & \text{if }(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B}),\\ \displaystyle 0 & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\mathbf{p},\mathbf{q}):=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D713}(|\mathbf{q}|) & \text{if }(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B}),\\ \displaystyle 0 & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
gives the following.
Theorem 7. Let
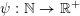 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function such that
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function such that
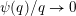 $\unicode[STIX]{x1D713}(q)/q\rightarrow 0$
as
$\unicode[STIX]{x1D713}(q)/q\rightarrow 0$
as
![]() $q\rightarrow \infty$
. Let
$q\rightarrow \infty$
. Let
![]() $\unicode[STIX]{x1D70B}$
be any partition of
$\unicode[STIX]{x1D70B}$
be any partition of
 $\{1,\ldots ,m+n\}$
and let
$\{1,\ldots ,m+n\}$
and let
 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
and
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
and
![]() $\mathbf{y}\in \mathbb{I}^{m}$
be fixed. Let
$\mathbf{y}\in \mathbb{I}^{m}$
be fixed. Let
![]() $f$
and
$f$
and
 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that
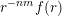 $r^{-nm}f(r)$
is monotonic and let
$r^{-nm}f(r)$
is monotonic and let
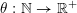 $\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be defined by
$\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be defined by
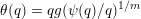 $\unicode[STIX]{x1D703}(q)=qg(\unicode[STIX]{x1D713}(q)/q)^{1/m}$
. Then
$\unicode[STIX]{x1D703}(q)=qg(\unicode[STIX]{x1D713}(q)/q)^{1/m}$
. Then
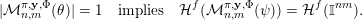 $$\begin{eqnarray}|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D703})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D703})|=1\quad \text{implies}\quad {\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm}).\end{eqnarray}$$
Now, let us turn our attention to the results of Dani, Laurent and Nogueira from [Reference Dani, Laurent and NogueiraDLN15]. For the moment, we will return to the homogeneous setting. Given a partition
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $\{1,\ldots ,m+n\}$
and an approximating function
$\{1,\ldots ,m+n\}$
and an approximating function
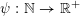 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
we will denote by
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
we will denote by
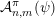 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})$
the set of
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})$
the set of
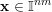 $\mathbf{x}\in \mathbb{I}^{nm}$
such that
$\mathbf{x}\in \mathbb{I}^{nm}$
such that
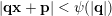 $$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\end{eqnarray}$$
$$\begin{eqnarray}|\mathbf{q}\mathbf{x}+\mathbf{p}|<\unicode[STIX]{x1D713}(|\mathbf{q}|)\end{eqnarray}$$
holds for
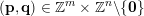 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
![]() $|\mathbf{q}|$
and
$|\mathbf{q}|$
and
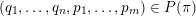 $(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
. We note that in this case the inequality holds for
$(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
. We note that in this case the inequality holds for
 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with arbitrarily large
![]() $|\mathbf{q}|$
if and only if the inequality holds for infinitely many
$|\mathbf{q}|$
if and only if the inequality holds for infinitely many
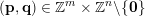 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. The notation
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. The notation
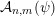 ${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
will be used as defined in § 2.1. The following statement is a consequence of [Reference Dani, Laurent and NogueiraDLN15, Theorem 1.2].
${\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
will be used as defined in § 2.1. The following statement is a consequence of [Reference Dani, Laurent and NogueiraDLN15, Theorem 1.2].
Theorem DLN1. Let
 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
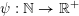 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
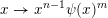 $x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then,
$x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then,
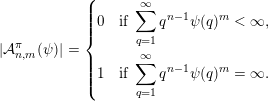 $$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})|=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty ,\\ 1 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty .\end{array}\right.\end{eqnarray}$$
The following Hausdorff measure analogue of Theorem DLN1 follows from Theorem 7.
Theorem 8. Let
 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
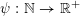 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
![]() $f$
and
$f$
and
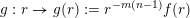 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
 $r^{-nm}f(r)$
is monotonic and
$r^{-nm}f(r)$
is monotonic and
 $q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then,
$q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then,
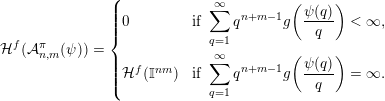 $$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}0 & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)<\infty ,\\ {\mathcal{H}}^{f}(\mathbb{I}^{nm}) & \text{if }\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{array}\right.\end{eqnarray}$$
Proof. First note that in light of the fact that
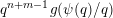 $q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing we may assume without loss of generality that
$q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing we may assume without loss of generality that
 $\unicode[STIX]{x1D713}(q)/q\rightarrow 0$
as
$\unicode[STIX]{x1D713}(q)/q\rightarrow 0$
as
![]() $q\rightarrow \infty$
. To see this, suppose that
$q\rightarrow \infty$
. To see this, suppose that
 $\unicode[STIX]{x1D713}(q)/q{\nrightarrow}0$
. Therefore, there must exist some
$\unicode[STIX]{x1D713}(q)/q{\nrightarrow}0$
. Therefore, there must exist some
![]() $\unicode[STIX]{x1D700}>0$
such that
$\unicode[STIX]{x1D700}>0$
such that
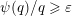 $\unicode[STIX]{x1D713}(q)/q\geqslant \unicode[STIX]{x1D700}$
infinitely often. In turn, since
$\unicode[STIX]{x1D713}(q)/q\geqslant \unicode[STIX]{x1D700}$
infinitely often. In turn, since
![]() $g$
is a dimension function, and hence non-decreasing, this means that
$g$
is a dimension function, and hence non-decreasing, this means that
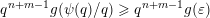 $q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)\geqslant q^{n+m-1}g(\unicode[STIX]{x1D700})$
infinitely often. However, since this expression is non-increasing, we must have that
$q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)\geqslant q^{n+m-1}g(\unicode[STIX]{x1D700})$
infinitely often. However, since this expression is non-increasing, we must have that
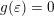 $g(\unicode[STIX]{x1D700})=0$
. In particular, this means that
$g(\unicode[STIX]{x1D700})=0$
. In particular, this means that
 $g(r)=0$
and, hence, also
$g(r)=0$
and, hence, also
 $f(r)=0$
for all
$f(r)=0$
for all
![]() $r\leqslant \unicode[STIX]{x1D700}$
. Thus
$r\leqslant \unicode[STIX]{x1D700}$
. Thus
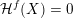 ${\mathcal{H}}^{f}(X)=0$
for any
${\mathcal{H}}^{f}(X)=0$
for any
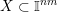 $X\subset \mathbb{I}^{nm}$
and so the result is trivially true.
$X\subset \mathbb{I}^{nm}$
and so the result is trivially true.
In view of the conditions imposed on
![]() $\unicode[STIX]{x1D70B}$
, we must have that
$\unicode[STIX]{x1D70B}$
, we must have that
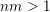 $nm>1$
. Furthermore, since
$nm>1$
. Furthermore, since
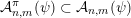 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
, it follows from Theorem 2 that
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})\subset {\mathcal{A}}_{n,m}(\unicode[STIX]{x1D713})$
, it follows from Theorem 2 that
 ${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))=0$
when
${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))=0$
when
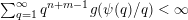 $\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
. Alternatively, one can use a standard covering argument to obtain a direct proof of the convergence part of Theorem 8.
$\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
. Alternatively, one can use a standard covering argument to obtain a direct proof of the convergence part of Theorem 8.
Regarding the divergence case, observe that
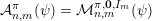 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})={\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D713})$
, where
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})={\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D713})$
, where
![]() $I_{m}$
represents the
$I_{m}$
represents the
![]() $m\times m$
identity matrix. Therefore, if
$m\times m$
identity matrix. Therefore, if
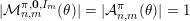 $|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D703})|=|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D703})|=1$
where
$|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D703})|=|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D703})|=1$
where
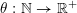 $\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
is defined by
$\unicode[STIX]{x1D703}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
is defined by
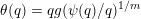 $\unicode[STIX]{x1D703}(q)=qg(\unicode[STIX]{x1D713}(q)/q)^{1/m}$
, then it would follow from Theorem 7 that
$\unicode[STIX]{x1D703}(q)=qg(\unicode[STIX]{x1D713}(q)/q)^{1/m}$
, then it would follow from Theorem 7 that
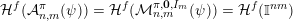 ${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
.
${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{0},I_{m}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
.
Now, by Theorem DLN1,
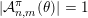 $|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D703})|=1$
if
$|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D703})|=1$
if
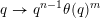 $q\rightarrow q^{n-1}\unicode[STIX]{x1D703}(q)^{m}$
is non-increasing and
$q\rightarrow q^{n-1}\unicode[STIX]{x1D703}(q)^{m}$
is non-increasing and
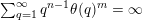 $\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\infty$
. We have that
$\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\infty$
. We have that
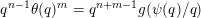 $q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
which is non-increasing by assumption. By our hypotheses, we also have
$q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
which is non-increasing by assumption. By our hypotheses, we also have
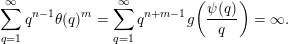 $$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D703}(q)^{m}=\mathop{\sum }_{q=1}^{\infty }q^{n+m-1}g\biggl(\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr)=\infty .\end{eqnarray}$$
Hence the proof is complete. ◻
If
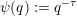 $\unicode[STIX]{x1D713}(q):=q^{-\unicode[STIX]{x1D70F}}$
for some
$\unicode[STIX]{x1D713}(q):=q^{-\unicode[STIX]{x1D70F}}$
for some
![]() $\unicode[STIX]{x1D70F}>0$
let us write
$\unicode[STIX]{x1D70F}>0$
let us write
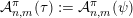 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}):={\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})$
. The following result regarding the Hausdorff dimension of
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}):={\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D713})$
. The following result regarding the Hausdorff dimension of
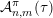 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F})$
is a corollary of Theorem 8.
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F})$
is a corollary of Theorem 8.
Corollary 1. Let
 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Then
$m+1$
elements. Then
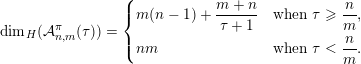 $$\begin{eqnarray}\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=\left\{\begin{array}{@{}ll@{}}\displaystyle m(n-1)+\frac{m+n}{\unicode[STIX]{x1D70F}+1} & \text{when }\unicode[STIX]{x1D70F}\geqslant \displaystyle \frac{n}{m},\\ nm & \text{when }\unicode[STIX]{x1D70F}<\displaystyle \frac{n}{m}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=\left\{\begin{array}{@{}ll@{}}\displaystyle m(n-1)+\frac{m+n}{\unicode[STIX]{x1D70F}+1} & \text{when }\unicode[STIX]{x1D70F}\geqslant \displaystyle \frac{n}{m},\\ nm & \text{when }\unicode[STIX]{x1D70F}<\displaystyle \frac{n}{m}.\end{array}\right.\end{eqnarray}$$
Proof. For
 $\unicode[STIX]{x1D70F}\geqslant n/m$
the result follows on applying Theorem 8 with
$\unicode[STIX]{x1D70F}\geqslant n/m$
the result follows on applying Theorem 8 with
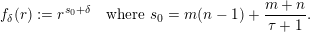 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FF}}(r):=r^{s_{0}+\unicode[STIX]{x1D6FF}}\quad \text{where }s_{0}=m(n-1)+\frac{m+n}{\unicode[STIX]{x1D70F}+1}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FF}}(r):=r^{s_{0}+\unicode[STIX]{x1D6FF}}\quad \text{where }s_{0}=m(n-1)+\frac{m+n}{\unicode[STIX]{x1D70F}+1}.\end{eqnarray}$$
Indeed, with
![]() $\unicode[STIX]{x1D6FF}$
sufficiently small, all the conditions of Theorem 8 are met and furthermore, as is easily seen, we have from Theorem 8 that
$\unicode[STIX]{x1D6FF}$
sufficiently small, all the conditions of Theorem 8 are met and furthermore, as is easily seen, we have from Theorem 8 that
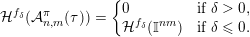 $$\begin{eqnarray}{\mathcal{H}}^{f_{\unicode[STIX]{x1D6FF}}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=\left\{\begin{array}{@{}lc@{}}\displaystyle 0 & \text{if }\unicode[STIX]{x1D6FF}>0,\\ \displaystyle {\mathcal{H}}^{f_{\unicode[STIX]{x1D6FF}}}(\mathbb{I}^{nm}) & \text{if }\unicode[STIX]{x1D6FF}\leqslant 0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f_{\unicode[STIX]{x1D6FF}}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=\left\{\begin{array}{@{}lc@{}}\displaystyle 0 & \text{if }\unicode[STIX]{x1D6FF}>0,\\ \displaystyle {\mathcal{H}}^{f_{\unicode[STIX]{x1D6FF}}}(\mathbb{I}^{nm}) & \text{if }\unicode[STIX]{x1D6FF}\leqslant 0.\end{array}\right.\end{eqnarray}$$
This means that
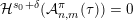 ${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=0$
for
${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=0$
for
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
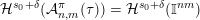 ${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))={\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}(\mathbb{I}^{nm})$
for
${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))={\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}(\mathbb{I}^{nm})$
for
![]() $\unicode[STIX]{x1D6FF}\leqslant 0$
. Therefore, if
$\unicode[STIX]{x1D6FF}\leqslant 0$
. Therefore, if
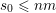 $s_{0}\leqslant nm$
then
$s_{0}\leqslant nm$
then
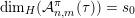 $\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=s_{0}$
since, in this case,
$\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=s_{0}$
since, in this case,
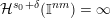 ${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}(\mathbb{I}^{nm})=\infty$
whenever
${\mathcal{H}}^{s_{0}+\unicode[STIX]{x1D6FF}}(\mathbb{I}^{nm})=\infty$
whenever
![]() $\unicode[STIX]{x1D6FF}<0$
. Finally, note that
$\unicode[STIX]{x1D6FF}<0$
. Finally, note that
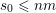 $s_{0}\leqslant nm$
if and only if
$s_{0}\leqslant nm$
if and only if
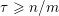 $\unicode[STIX]{x1D70F}\geqslant n/m$
.
$\unicode[STIX]{x1D70F}\geqslant n/m$
.
In the case where
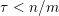 $\unicode[STIX]{x1D70F}<n/m$
observe that
$\unicode[STIX]{x1D70F}<n/m$
observe that
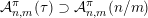 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F})\supset {\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(n/m)$
so
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F})\supset {\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(n/m)$
so
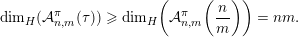 $$\begin{eqnarray}\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))\geqslant \dim _{H}\biggl({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}\biggl(\frac{n}{m}\biggr)\biggr)=nm.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))\geqslant \dim _{H}\biggl({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}\biggl(\frac{n}{m}\biggr)\biggr)=nm.\end{eqnarray}$$
Combining this with the trivial upper bound gives
 $\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=nm$
when
$\dim _{H}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70F}))=nm$
when
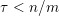 $\unicode[STIX]{x1D70F}<n/m$
, as required.◻
$\unicode[STIX]{x1D70F}<n/m$
, as required.◻
Next we consider two results of Dani, Laurent and Nogueira regarding inhomogeneous approximation. As before, for a fixed
![]() $\mathbf{y}\in \mathbb{I}^{m}$
we let
$\mathbf{y}\in \mathbb{I}^{m}$
we let
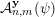 ${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})$
denote the set of points
${\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})$
denote the set of points
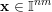 $\mathbf{x}\in \mathbb{I}^{nm}$
for which
$\mathbf{x}\in \mathbb{I}^{nm}$
for which
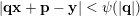 $$\begin{eqnarray}\displaystyle |\mathbf{q}\mathbf{x}+\mathbf{p}-\mathbf{y}|<\unicode[STIX]{x1D713}(|\mathbf{q}|) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathbf{q}\mathbf{x}+\mathbf{p}-\mathbf{y}|<\unicode[STIX]{x1D713}(|\mathbf{q}|) & & \displaystyle\end{eqnarray}$$
holds for infinitely many
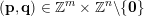 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Given a partition
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
. Given a partition
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $\{1,\ldots ,m+n\}$
, let
$\{1,\ldots ,m+n\}$
, let
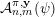 ${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713})$
be the set of points
${\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713})$
be the set of points
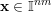 $\mathbf{x}\in \mathbb{I}^{nm}$
for which (17) holds for infinitely many
$\mathbf{x}\in \mathbb{I}^{nm}$
for which (17) holds for infinitely many
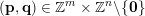 $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m}\times \mathbb{Z}^{n}\setminus \{\mathbf{0}\}$
with
 $(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
.
$(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{m})\in P(\unicode[STIX]{x1D70B})$
.
Rephrasing it in a way which is more suitable for our current purposes, a consequence of [Reference Dani, Laurent and NogueiraDLN15, Theorem 1.1] reads as follows.
Theorem DLN2. Let
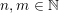 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
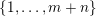 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
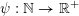 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
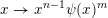 $x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then,
$x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then,
(i) if
 $\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty$
then for almost every
$\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty$
then for almost every
 $\mathbf{y}\in \mathbb{I}^{m}$
we have
$\mathbf{y}\in \mathbb{I}^{m}$
we have
 $|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713})|=1$
;
$|{\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713})|=1$
;(ii) if
 $\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty$
then for any
$\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty$
then for any
 $\mathbf{y}\in \mathbb{I}^{m}$
we have
$\mathbf{y}\in \mathbb{I}^{m}$
we have
 $|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})|=0$
.
$|{\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713})|=0$
.
The corresponding Hausdorff measure statement we obtain in this case is as follows.
Theorem 9. Let
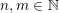 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
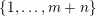 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
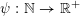 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
![]() $f$
and
$f$
and
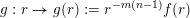 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
 $r^{-nm}f(r)$
is monotonic and
$r^{-nm}f(r)$
is monotonic and
 $q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then,
$q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then,
(i) if
 $\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)=\infty$
then for Lebesgue almost every
$\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)=\infty$
then for Lebesgue almost every
 $\mathbf{y}\in \mathbb{I}^{m}$
we have
$\mathbf{y}\in \mathbb{I}^{m}$
we have
 ${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
;
${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
;(ii) if
 $\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
then for any
$\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
then for any
 $\mathbf{y}\in \mathbb{I}^{m}$
we have
$\mathbf{y}\in \mathbb{I}^{m}$
we have
 ${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))=0$
.
${\mathcal{H}}^{f}({\mathcal{A}}_{n,m}^{\mathbf{y}}(\unicode[STIX]{x1D713}))=0$
.
Proof. This is similar to the proof of Theorem 8 with the only difference being the introduction of
![]() $\mathbf{y}$
.◻
$\mathbf{y}$
.◻
Finally, let us reintroduce the parameter
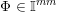 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
. In this case, considering the sets
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
. In this case, considering the sets
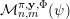 ${\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
(as defined on p. 13), it follows from [Reference Dani, Laurent and NogueiraDLN15, Theorem 1.3] that we have:
${\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})$
(as defined on p. 13), it follows from [Reference Dani, Laurent and NogueiraDLN15, Theorem 1.3] that we have:
Theorem DLN3. Let
 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
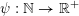 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be a function such that the mapping
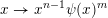 $x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then, for any
$x\rightarrow x^{n-1}\unicode[STIX]{x1D713}(x)^{m}$
is non-increasing. Then, for any
![]() $\mathbf{y}\in \mathbb{I}^{m}$
,
$\mathbf{y}\in \mathbb{I}^{m}$
,
(i) if
 $\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty$
then for almost every
$\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}=\infty$
then for almost every
 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have that
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have that
 $|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})|=1$
;
$|{\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})|=1$
;(ii) if
 $\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty$
then for any
$\sum _{q=1}^{\infty }q^{n-1}\unicode[STIX]{x1D713}(q)^{m}<\infty$
then for any
 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have
 $|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})|=0$
.
$|{\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713})|=0$
.
Combining this with Theorem 7 we obtain the following Hausdorff measure statement.
Theorem 10. Let
 $n,m\in \mathbb{N}$
and let
$n,m\in \mathbb{N}$
and let
![]() $\unicode[STIX]{x1D70B}$
be a partition of
$\unicode[STIX]{x1D70B}$
be a partition of
 $\{1,\ldots ,m+n\}$
such that every component of
$\{1,\ldots ,m+n\}$
such that every component of
![]() $\unicode[STIX]{x1D70B}$
has at least
$\unicode[STIX]{x1D70B}$
has at least
![]() $m+1$
elements. Let
$m+1$
elements. Let
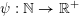 $\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be an approximating function. Let
![]() $f$
and
$f$
and
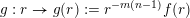 $g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
$g:r\rightarrow g(r):=r^{-m(n-1)}f(r)$
be dimension functions such that the function
 $r^{-nm}f(r)$
is monotonic and
$r^{-nm}f(r)$
is monotonic and
 $q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then, for any
$q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)$
is non-increasing. Then, for any
![]() $\mathbf{y}\in \mathbb{I}^{m}$
,
$\mathbf{y}\in \mathbb{I}^{m}$
,
(i) if
 $\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)=\infty$
then for Lebesgue almost every
$\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)=\infty$
then for Lebesgue almost every
 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have that
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
we have that
 ${\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
;
${\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\unicode[STIX]{x1D70B},\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))={\mathcal{H}}^{f}(\mathbb{I}^{nm})$
;(ii) if
 $\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
then, for any
$\sum _{q=1}^{\infty }q^{n+m-1}g(\unicode[STIX]{x1D713}(q)/q)<\infty$
then, for any
 $\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
, we have that
$\unicode[STIX]{x1D6F7}\in \mathbb{I}^{mm}$
, we have that
 ${\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))=0$
.
${\mathcal{H}}^{f}({\mathcal{M}}_{n,m}^{\mathbf{y},\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D713}))=0$
.
Proof. Once again the proof is similar to that of Theorem 8. ◻
3 Preliminaries to the Proof of Theorem 1
3.1 Hausdorff measures
In this section we give a brief account of Hausdorff measures and dimension. Throughout, by a dimension function
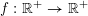 $f:\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$
we shall mean a left continuous, non-decreasing function such that
$f:\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$
we shall mean a left continuous, non-decreasing function such that
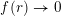 $f(r)\rightarrow 0$
as
$f(r)\rightarrow 0$
as
![]() $r\rightarrow 0$
. Given a ball
$r\rightarrow 0$
. Given a ball
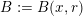 $B:=B(x,r)$
in
$B:=B(x,r)$
in
![]() $\mathbb{R}^{k}$
, we define
$\mathbb{R}^{k}$
, we define
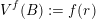 $$\begin{eqnarray}V^{f}(B):=f(r)\end{eqnarray}$$
$$\begin{eqnarray}V^{f}(B):=f(r)\end{eqnarray}$$
and refer to
![]() $V^{f}(B)$
as the
$V^{f}(B)$
as the
![]() $f$
-volume of
$f$
-volume of
![]() $B$
. Note that if
$B$
. Note that if
![]() $m$
is
$m$
is
![]() $k$
-dimensional Lebesgue measure and
$k$
-dimensional Lebesgue measure and
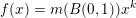 $f(x)=m(B(0,1))x^{k}$
, then
$f(x)=m(B(0,1))x^{k}$
, then
![]() $V^{f}$
is simply the volume of
$V^{f}$
is simply the volume of
![]() $B$
in the usual geometric sense; i.e.
$B$
in the usual geometric sense; i.e.
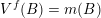 $V^{f}(B)=m(B)$
. In the case when
$V^{f}(B)=m(B)$
. In the case when
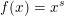 $f(x)=x^{s}$
for some
$f(x)=x^{s}$
for some
![]() $s\geqslant 0$
, we write
$s\geqslant 0$
, we write
![]() $V^{s}$
for
$V^{s}$
for
![]() $V^{f}$
.
$V^{f}$
.
The Hausdorff
![]() $f$
-measure with respect to the dimension function
$f$
-measure with respect to the dimension function
![]() $f$
will be denoted throughout by
$f$
will be denoted throughout by
![]() ${\mathcal{H}}^{f}$
and is defined as follows. Suppose
${\mathcal{H}}^{f}$
and is defined as follows. Suppose
![]() $F$
is a subset of
$F$
is a subset of
![]() $\mathbb{R}^{k}$
. For
$\mathbb{R}^{k}$
. For
![]() $\unicode[STIX]{x1D70C}>0$
, a countable collection
$\unicode[STIX]{x1D70C}>0$
, a countable collection
![]() $\{B_{i}\}$
of balls in
$\{B_{i}\}$
of balls in
![]() $\mathbb{R}^{k}$
with radii
$\mathbb{R}^{k}$
with radii
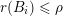 $r(B_{i})\leqslant \unicode[STIX]{x1D70C}$
for each
$r(B_{i})\leqslant \unicode[STIX]{x1D70C}$
for each
![]() $i$
such that
$i$
such that
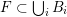 $F\subset \bigcup _{i}B_{i}$
is called a
$F\subset \bigcup _{i}B_{i}$
is called a
![]() $\unicode[STIX]{x1D70C}$
-cover for
$\unicode[STIX]{x1D70C}$
-cover for
![]() $F$
. Clearly such a cover exists for every
$F$
. Clearly such a cover exists for every
![]() $\unicode[STIX]{x1D70C}>0$
. For a dimension function
$\unicode[STIX]{x1D70C}>0$
. For a dimension function
![]() $f$
define
$f$
define
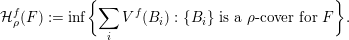 $$\begin{eqnarray}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F):=\inf \biggl\{\mathop{\sum }_{i}V^{f}(B_{i}):\{B_{i}\}\text{is a }\unicode[STIX]{x1D70C}\text{-cover for }F\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F):=\inf \biggl\{\mathop{\sum }_{i}V^{f}(B_{i}):\{B_{i}\}\text{is a }\unicode[STIX]{x1D70C}\text{-cover for }F\biggr\}.\end{eqnarray}$$
The Hausdorff
![]() $f$
-measure,
$f$
-measure,
![]() ${\mathcal{H}}^{f}(F)$
, of
${\mathcal{H}}^{f}(F)$
, of
![]() $F$
with respect to the dimension function
$F$
with respect to the dimension function
![]() $f$
is defined by
$f$
is defined by
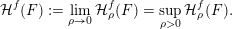 $$\begin{eqnarray}{\mathcal{H}}^{f}(F):=\lim _{\unicode[STIX]{x1D70C}\rightarrow 0}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F)=\sup _{\unicode[STIX]{x1D70C}>0}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(F):=\lim _{\unicode[STIX]{x1D70C}\rightarrow 0}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F)=\sup _{\unicode[STIX]{x1D70C}>0}{\mathcal{H}}_{\unicode[STIX]{x1D70C}}^{f}(F).\end{eqnarray}$$
A simple consequence of the definition of
![]() ${\mathcal{H}}^{f}$
is the following useful fact (see, for example, [Reference FalconerFal03]).
${\mathcal{H}}^{f}$
is the following useful fact (see, for example, [Reference FalconerFal03]).
Lemma 1. If
![]() $f$
and
$f$
and
![]() $g$
are two dimension functions such that the ratio
$g$
are two dimension functions such that the ratio
 $f(r)/g(r)\rightarrow 0$
as
$f(r)/g(r)\rightarrow 0$
as
![]() $r\rightarrow 0$
, then
$r\rightarrow 0$
, then
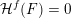 ${\mathcal{H}}^{f}(F)=0$
whenever
${\mathcal{H}}^{f}(F)=0$
whenever
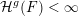 ${\mathcal{H}}^{g}(F)<\infty$
.
${\mathcal{H}}^{g}(F)<\infty$
.
In the case that
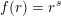 $f(r)=r^{s}$
(
$f(r)=r^{s}$
(
![]() $s\geqslant 0$
), the measure
$s\geqslant 0$
), the measure
![]() ${\mathcal{H}}^{f}$
is the usual
${\mathcal{H}}^{f}$
is the usual
![]() $s$
-dimensional Hausdorff measure
$s$
-dimensional Hausdorff measure
![]() ${\mathcal{H}}^{s}$
and the Hausdorff dimension,
${\mathcal{H}}^{s}$
and the Hausdorff dimension,
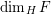 $\dim _{H}F$
, of a set
$\dim _{H}F$
, of a set
![]() $F$
is defined by
$F$
is defined by
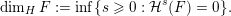 $$\begin{eqnarray}\dim _{H}F:=\inf \{s\geqslant 0:{\mathcal{H}}^{s}(F)=0\}.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{H}F:=\inf \{s\geqslant 0:{\mathcal{H}}^{s}(F)=0\}.\end{eqnarray}$$
For subsets of
![]() $\mathbb{R}^{k}$
,
$\mathbb{R}^{k}$
,
![]() ${\mathcal{H}}^{k}$
is comparable to the
${\mathcal{H}}^{k}$
is comparable to the
![]() $k$
-dimensional Lebesgue measure. Actually,
$k$
-dimensional Lebesgue measure. Actually,
![]() ${\mathcal{H}}^{k}$
is a constant multiple of the
${\mathcal{H}}^{k}$
is a constant multiple of the
![]() $k$
-dimensional Lebesgue measure (but we shall not need this stronger statement).
$k$
-dimensional Lebesgue measure (but we shall not need this stronger statement).
Furthermore, for any ball
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{k}$
we have that
$\mathbb{R}^{k}$
we have that
![]() $V^{k}(B)$
is comparable to
$V^{k}(B)$
is comparable to
![]() $|B|$
. Thus there are constants
$|B|$
. Thus there are constants
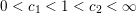 $0<c_{1}<1<c_{2}<\infty$
such that for any ball
$0<c_{1}<1<c_{2}<\infty$
such that for any ball
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{k}$
we have
$\mathbb{R}^{k}$
we have
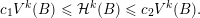 $$\begin{eqnarray}\displaystyle c_{1}V^{k}(B)\leqslant {\mathcal{H}}^{k}(B)\leqslant c_{2}V^{k}(B). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{1}V^{k}(B)\leqslant {\mathcal{H}}^{k}(B)\leqslant c_{2}V^{k}(B). & & \displaystyle\end{eqnarray}$$
A general and classical method for obtaining a lower bound for the Hausdorff
![]() $f$
-measure of an arbitrary set
$f$
-measure of an arbitrary set
![]() $F$
is the following mass distribution principle. This will play a central role in our proof of Theorem 1 in § 5.
$F$
is the following mass distribution principle. This will play a central role in our proof of Theorem 1 in § 5.
Lemma 2 (Mass distribution principle).
Let
![]() $\unicode[STIX]{x1D707}$
be a probability measure supported on a subset
$\unicode[STIX]{x1D707}$
be a probability measure supported on a subset
![]() $F$
of
$F$
of
![]() $\mathbb{R}^{k}$
. Suppose there are positive constants
$\mathbb{R}^{k}$
. Suppose there are positive constants
![]() $c$
and
$c$
and
![]() $r_{o}$
such that
$r_{o}$
such that
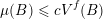 $$\begin{eqnarray}\unicode[STIX]{x1D707}(B)\leqslant cV^{f}(B)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(B)\leqslant cV^{f}(B)\end{eqnarray}$$
for any ball
![]() $B$
with radius
$B$
with radius
![]() $r\leqslant r_{o}$
. If
$r\leqslant r_{o}$
. If
![]() $E$
is a subset of
$E$
is a subset of
![]() $F$
with
$F$
with
 $\unicode[STIX]{x1D707}(E)=\unicode[STIX]{x1D706}>0$
then
$\unicode[STIX]{x1D707}(E)=\unicode[STIX]{x1D706}>0$
then
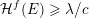 ${\mathcal{H}}^{f}(E)\geqslant \unicode[STIX]{x1D706}/c$
.
${\mathcal{H}}^{f}(E)\geqslant \unicode[STIX]{x1D706}/c$
.
The above lemma is stated as it appears in [Reference Beresnevich and VelaniBV06a] since this version is most useful for our current purposes. For further information in general regarding Hausdorff measures and dimension we refer the reader to [Reference FalconerFal03, Reference MattilaMat95].
3.2 The 5
 $r$
-covering lemma
$r$
-covering lemma
Let
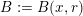 $B:=B(x,r)$
be a ball in
$B:=B(x,r)$
be a ball in
![]() $\mathbb{R}^{k}$
. For any
$\mathbb{R}^{k}$
. For any
![]() $\unicode[STIX]{x1D706}>0$
, we denote by
$\unicode[STIX]{x1D706}>0$
, we denote by
![]() $\unicode[STIX]{x1D706}B$
the ball
$\unicode[STIX]{x1D706}B$
the ball
![]() $B$
scaled by a factor
$B$
scaled by a factor
![]() $\unicode[STIX]{x1D706}$
; i.e.
$\unicode[STIX]{x1D706}$
; i.e.
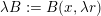 $\unicode[STIX]{x1D706}B:=B(x,\unicode[STIX]{x1D706}r)$
.
$\unicode[STIX]{x1D706}B:=B(x,\unicode[STIX]{x1D706}r)$
.
We conclude this section by stating a basic, but extremely useful, covering lemma which we will use throughout [Reference MattilaMat95].
Lemma 3 (The
 $5r$
-covering lemma).
$5r$
-covering lemma).
Every family
![]() ${\mathcal{F}}$
of balls of uniformly bounded diameter in
${\mathcal{F}}$
of balls of uniformly bounded diameter in
![]() $\mathbb{R}^{k}$
contains a disjoint subfamily
$\mathbb{R}^{k}$
contains a disjoint subfamily
![]() ${\mathcal{G}}$
such that
${\mathcal{G}}$
such that
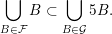 $$\begin{eqnarray}\mathop{\bigcup }_{B\in {\mathcal{F}}}B\subset \mathop{\bigcup }_{B\in {\mathcal{G}}}5B.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{B\in {\mathcal{F}}}B\subset \mathop{\bigcup }_{B\in {\mathcal{G}}}5B.\end{eqnarray}$$
4 The
 $K_{G,B}$
covering lemma
$K_{G,B}$
covering lemma
Our strategy for proving Theorem 1 is similar to that used for proving the mass transference principle for balls in [Reference Beresnevich and VelaniBV06a]. There are however various technical differences that account for the different shape of approximating sets. First of all we will require a covering lemma analogous to the
![]() $K_{G,B}$
-lemma established in [Reference Beresnevich and VelaniBV06a, § 4]. This appears as Lemma 4 below. The balls obtained from Lemma 4 correspond to planes in the
$K_{G,B}$
-lemma established in [Reference Beresnevich and VelaniBV06a, § 4]. This appears as Lemma 4 below. The balls obtained from Lemma 4 correspond to planes in the
![]() $\limsup$
set
$\limsup$
set
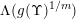 $\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})$
. Furthermore, for the proof of Theorem 1 it is necessary for us to obtain from each of these ‘larger’ balls a collection of balls which correspond to the ‘shrunk’
$\unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m})$
. Furthermore, for the proof of Theorem 1 it is necessary for us to obtain from each of these ‘larger’ balls a collection of balls which correspond to the ‘shrunk’
![]() $\limsup$
set
$\limsup$
set
![]() $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
. The desired properties of this collection and the existence of such a collection are the contents of Lemma 5 of this section.
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
. The desired properties of this collection and the existence of such a collection are the contents of Lemma 5 of this section.
To save on notation, throughout let
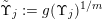 $\tilde{\unicode[STIX]{x1D6F6}}_{j}:=g(\unicode[STIX]{x1D6F6}_{j})^{1/m}$
. For an arbitrary ball
$\tilde{\unicode[STIX]{x1D6F6}}_{j}:=g(\unicode[STIX]{x1D6F6}_{j})^{1/m}$
. For an arbitrary ball
![]() $B\in \mathbb{R}^{k}$
and for each
$B\in \mathbb{R}^{k}$
and for each
![]() $j\in \mathbb{N}$
define
$j\in \mathbb{N}$
define
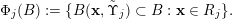 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}(B):=\{B(\mathbf{x},\tilde{\unicode[STIX]{x1D6F6}}_{j})\subset B:\mathbf{x}\in R_{j}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}(B):=\{B(\mathbf{x},\tilde{\unicode[STIX]{x1D6F6}}_{j})\subset B:\mathbf{x}\in R_{j}\}.\end{eqnarray}$$
Analogously to [Reference Beresnevich and VelaniBV06a, Lemma 5] we will require the following covering lemma.
Lemma 4. Let
![]() ${\mathcal{R}}$
,
${\mathcal{R}}$
,
![]() $\unicode[STIX]{x1D6F6}$
,
$\unicode[STIX]{x1D6F6}$
,
![]() $g$
and
$g$
and
![]() $\unicode[STIX]{x1D6FA}$
be as in Theorem 1 and assume that (2) is satisfied. Then for any ball
$\unicode[STIX]{x1D6FA}$
be as in Theorem 1 and assume that (2) is satisfied. Then for any ball
![]() $B$
in
$B$
in
![]() $\unicode[STIX]{x1D6FA}$
and any
$\unicode[STIX]{x1D6FA}$
and any
![]() $G\in \mathbb{N}$
, there exists a finite collection
$G\in \mathbb{N}$
, there exists a finite collection
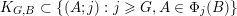 $$\begin{eqnarray}K_{G,B}\subset \{(A;j):j\geqslant G,A\in \unicode[STIX]{x1D6F7}_{j}(B)\}\end{eqnarray}$$
$$\begin{eqnarray}K_{G,B}\subset \{(A;j):j\geqslant G,A\in \unicode[STIX]{x1D6F7}_{j}(B)\}\end{eqnarray}$$
satisfying the following properties:
(i) if
 $(A;j)\in K_{G,B}$
then
$(A;j)\in K_{G,B}$
then
 $3A\subset B$
;
$3A\subset B$
;(ii) if
 $(A;j),(A^{\prime };j^{\prime })\in K_{G,B}$
are distinct then
$(A;j),(A^{\prime };j^{\prime })\in K_{G,B}$
are distinct then
 $3A\cap 3A^{\prime }=\emptyset$
; and
$3A\cap 3A^{\prime }=\emptyset$
; and(iii)
 $\displaystyle {\mathcal{H}}^{k}\bigg(\bigcup _{(A;j)\in K_{G,B}}A\bigg)\geqslant \frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B)$
.
$\displaystyle {\mathcal{H}}^{k}\bigg(\bigcup _{(A;j)\in K_{G,B}}A\bigg)\geqslant \frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B)$
.
Remark 3. Essentially,
![]() $K_{G,B}$
is a collection of balls drawn from the families
$K_{G,B}$
is a collection of balls drawn from the families
![]() $\unicode[STIX]{x1D6F7}_{j}(B)$
. We write
$\unicode[STIX]{x1D6F7}_{j}(B)$
. We write
![]() $(A;j)$
for a generic ball from
$(A;j)$
for a generic ball from
![]() $K_{G,B}$
to ‘remember’ the index
$K_{G,B}$
to ‘remember’ the index
![]() $j$
of the family
$j$
of the family
![]() $\unicode[STIX]{x1D6F7}_{j}(B)$
that the ball
$\unicode[STIX]{x1D6F7}_{j}(B)$
that the ball
![]() $A$
comes from. However, when we are referring only to the ball
$A$
comes from. However, when we are referring only to the ball
![]() $A$
(as opposed to the pair
$A$
(as opposed to the pair
![]() $(A;j)$
) we will just write
$(A;j)$
) we will just write
![]() $A$
. Keeping track of the associated
$A$
. Keeping track of the associated
![]() $j$
will be absolutely necessary in order to be able to choose the ‘right’ collection of balls within
$j$
will be absolutely necessary in order to be able to choose the ‘right’ collection of balls within
![]() $A$
that at the same time lie in an
$A$
that at the same time lie in an
![]() $\unicode[STIX]{x1D6F6}_{j}$
-neighbourhood of the relevant
$\unicode[STIX]{x1D6F6}_{j}$
-neighbourhood of the relevant
![]() $R_{j}$
. Indeed, for
$R_{j}$
. Indeed, for
![]() $j\neq j^{\prime }$
we could have
$j\neq j^{\prime }$
we could have
![]() $A=A^{\prime }$
for some
$A=A^{\prime }$
for some
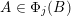 $A\in \unicode[STIX]{x1D6F7}_{j}(B)$
and
$A\in \unicode[STIX]{x1D6F7}_{j}(B)$
and
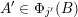 $A^{\prime }\in \unicode[STIX]{x1D6F7}_{j^{\prime }}(B)$
.
$A^{\prime }\in \unicode[STIX]{x1D6F7}_{j^{\prime }}(B)$
.
Proof of Lemma 4.
For each
![]() $j\in \mathbb{N}$
, consider the collection of balls
$j\in \mathbb{N}$
, consider the collection of balls
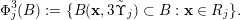 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}^{3}(B):=\{B(\mathbf{x},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\subset B:\mathbf{x}\in R_{j}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}^{3}(B):=\{B(\mathbf{x},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\subset B:\mathbf{x}\in R_{j}\}.\end{eqnarray}$$
By (2), for any
![]() $G\geqslant 1$
we have that
$G\geqslant 1$
we have that
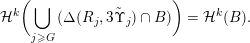 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}(\unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B)\biggr)={\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}(\unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B)\biggr)={\mathcal{H}}^{k}(B).\end{eqnarray}$$
Observe that
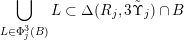 $$\begin{eqnarray}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B\end{eqnarray}$$
and that the difference of the two sets lies within
![]() $3\tilde{\unicode[STIX]{x1D6F6}}_{j}$
of the boundary of
$3\tilde{\unicode[STIX]{x1D6F6}}_{j}$
of the boundary of
![]() $B$
. Then, since
$B$
. Then, since
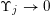 $\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
, and consequently
$\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
, and consequently
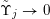 $\tilde{\unicode[STIX]{x1D6F6}}_{j}\rightarrow 0$
, as
$\tilde{\unicode[STIX]{x1D6F6}}_{j}\rightarrow 0$
, as
![]() $j\rightarrow \infty$
, we have that
$j\rightarrow \infty$
, we have that
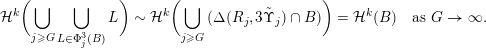 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\sim {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}(\unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B)\biggr)={\mathcal{H}}^{k}(B)\quad \text{as }G\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\sim {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}(\unicode[STIX]{x1D6E5}(R_{j},3\tilde{\unicode[STIX]{x1D6F6}}_{j})\cap B)\biggr)={\mathcal{H}}^{k}(B)\quad \text{as }G\rightarrow \infty .\end{eqnarray}$$
In particular, there exists a sufficiently large
![]() $G^{\prime }\in \mathbb{N}$
such that for any
$G^{\prime }\in \mathbb{N}$
such that for any
![]() $G\geqslant G^{\prime }$
we have
$G\geqslant G^{\prime }$
we have
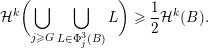 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\geqslant \frac{1}{2}{\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\geqslant \frac{1}{2}{\mathcal{H}}^{k}(B).\end{eqnarray}$$
However, for any
![]() $G<G^{\prime }$
we also have
$G<G^{\prime }$
we also have
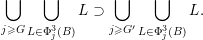 $$\begin{eqnarray}\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\supset \mathop{\bigcup }_{j\geqslant G^{\prime }}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\supset \mathop{\bigcup }_{j\geqslant G^{\prime }}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L.\end{eqnarray}$$
Thus, for any
![]() $G\in \mathbb{N}$
we must have
$G\in \mathbb{N}$
we must have
 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\geqslant \frac{1}{2}{\mathcal{H}}^{k}(B). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\geqslant \frac{1}{2}{\mathcal{H}}^{k}(B). & & \displaystyle\end{eqnarray}$$
In fact, using the same argument as above it is possible to show that for any
![]() $G\in \mathbb{N}$
we have
$G\in \mathbb{N}$
we have
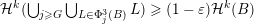 ${\mathcal{H}}^{k}(\bigcup _{j\geqslant G}\bigcup _{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L)\geqslant (1-\unicode[STIX]{x1D700}){\mathcal{H}}^{k}(B)$
for any
${\mathcal{H}}^{k}(\bigcup _{j\geqslant G}\bigcup _{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L)\geqslant (1-\unicode[STIX]{x1D700}){\mathcal{H}}^{k}(B)$
for any
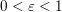 $0<\unicode[STIX]{x1D700}<1$
and hence that we must have
$0<\unicode[STIX]{x1D700}<1$
and hence that we must have
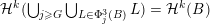 ${\mathcal{H}}^{k}(\bigcup _{j\geqslant G}\bigcup _{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L)={\mathcal{H}}^{k}(B)$
. However, (19) is sufficient for our purposes here.
${\mathcal{H}}^{k}(\bigcup _{j\geqslant G}\bigcup _{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L)={\mathcal{H}}^{k}(B)$
. However, (19) is sufficient for our purposes here.
By Lemma 3, there exists a disjoint subcollection
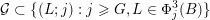 ${\mathcal{G}}\subset \{(L;j):j\geqslant G,L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)\}$
such that
${\mathcal{G}}\subset \{(L;j):j\geqslant G,L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)\}$
such that
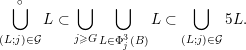 $$\begin{eqnarray}\mathop{\bigcup }_{(L;j)\in {\mathcal{G}}}^{\circ }L\subset \mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \mathop{\bigcup }_{(L;j)\in {\mathcal{G}}}5L.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{(L;j)\in {\mathcal{G}}}^{\circ }L\subset \mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \mathop{\bigcup }_{(L;j)\in {\mathcal{G}}}5L.\end{eqnarray}$$
Now, let
![]() ${\mathcal{G}}^{\prime }$
consist of all the balls from
${\mathcal{G}}^{\prime }$
consist of all the balls from
![]() ${\mathcal{G}}$
but shrunk by a factor of 3; so the balls in
${\mathcal{G}}$
but shrunk by a factor of 3; so the balls in
![]() ${\mathcal{G}}^{\prime }$
will still be disjoint when scaled by a factor of 3. Formally,
${\mathcal{G}}^{\prime }$
will still be disjoint when scaled by a factor of 3. Formally,
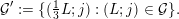 $$\begin{eqnarray}{\mathcal{G}}^{\prime }:=\{({\textstyle \frac{1}{3}}L;j):(L;j)\in {\mathcal{G}}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{G}}^{\prime }:=\{({\textstyle \frac{1}{3}}L;j):(L;j)\in {\mathcal{G}}\}.\end{eqnarray}$$
Then, we have that
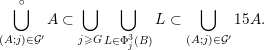 $$\begin{eqnarray}\displaystyle \mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}^{\circ }A\subset \mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}15A. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}^{\circ }A\subset \mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\subset \mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}15A. & & \displaystyle\end{eqnarray}$$
From (19) and (20) we have that
 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}A\biggr) & = & \displaystyle \mathop{\sum }_{(A;j)\in {\mathcal{G}}^{\prime }}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{(A;j)\in {\mathcal{G}}^{\prime }}\frac{1}{15^{k}}{\mathcal{H}}^{k}(15A)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}15A\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{2\times 15^{k}}{\mathcal{H}}^{k}(B).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}A\biggr) & = & \displaystyle \mathop{\sum }_{(A;j)\in {\mathcal{G}}^{\prime }}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{(A;j)\in {\mathcal{G}}^{\prime }}\frac{1}{15^{k}}{\mathcal{H}}^{k}(15A)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{(A;j)\in {\mathcal{G}}^{\prime }}15A\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{j\geqslant G}\mathop{\bigcup }_{L\in \unicode[STIX]{x1D6F7}_{j}^{3}(B)}L\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{2\times 15^{k}}{\mathcal{H}}^{k}(B).\nonumber\end{eqnarray}$$
Next note that, since the balls in
![]() ${\mathcal{G}}^{\prime }$
are disjoint and contained in
${\mathcal{G}}^{\prime }$
are disjoint and contained in
![]() $B$
and
$B$
and
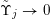 $\tilde{\unicode[STIX]{x1D6F6}}_{j}\rightarrow 0$
as
$\tilde{\unicode[STIX]{x1D6F6}}_{j}\rightarrow 0$
as
![]() $j\rightarrow \infty$
, we have that
$j\rightarrow \infty$
, we have that
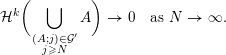 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in {\mathcal{G}}^{\prime } \\ j\geqslant N}}A\biggr)\rightarrow 0\quad \text{as }N\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in {\mathcal{G}}^{\prime } \\ j\geqslant N}}A\biggr)\rightarrow 0\quad \text{as }N\rightarrow \infty .\end{eqnarray}$$
Therefore, there exists a sufficiently large
![]() $N_{0}\in \mathbb{N}$
such that
$N_{0}\in \mathbb{N}$
such that
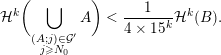 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in {\mathcal{G}}^{\prime } \\ j\geqslant N_{0}}}A\biggr)<\frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in {\mathcal{G}}^{\prime } \\ j\geqslant N_{0}}}A\biggr)<\frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B).\end{eqnarray}$$
Thus, taking
![]() $K_{G,B}$
to be the subcollection of
$K_{G,B}$
to be the subcollection of
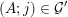 $(A;j)\in {\mathcal{G}}^{\prime }$
with
$(A;j)\in {\mathcal{G}}^{\prime }$
with
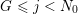 $G\leqslant j<N_{0}$
ensures that
$G\leqslant j<N_{0}$
ensures that
![]() $K_{G,B}$
is a finite collection of balls while still satisfying the required properties (i)–(iii).◻
$K_{G,B}$
is a finite collection of balls while still satisfying the required properties (i)–(iii).◻
Lemma 5. Let
![]() ${\mathcal{R}}$
,
${\mathcal{R}}$
,
![]() $\unicode[STIX]{x1D6F6}$
,
$\unicode[STIX]{x1D6F6}$
,
![]() $g$
,
$g$
,
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $B$
be as in Lemma 4 and assume that (2) is satisfied. Furthermore, assume that
$B$
be as in Lemma 4 and assume that (2) is satisfied. Furthermore, assume that
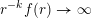 $r^{-k}f(r)\rightarrow \infty$
as
$r^{-k}f(r)\rightarrow \infty$
as
![]() $r\rightarrow 0$
. Let
$r\rightarrow 0$
. Let
![]() $K_{G,B}$
be as in Lemma 4. Then, provided that
$K_{G,B}$
be as in Lemma 4. Then, provided that
![]() $G$
is sufficiently large, for any
$G$
is sufficiently large, for any
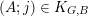 $(A;j)\in K_{G,B}$
there exists a collection
$(A;j)\in K_{G,B}$
there exists a collection
![]() ${\mathcal{C}}(A;j)$
of balls satisfying the following properties:
${\mathcal{C}}(A;j)$
of balls satisfying the following properties:
(i) each ball in
 ${\mathcal{C}}(A;j)$
is of radius
${\mathcal{C}}(A;j)$
is of radius
 $\unicode[STIX]{x1D6F6}_{j}$
and is centred on
$\unicode[STIX]{x1D6F6}_{j}$
and is centred on
 $R_{j};$
$R_{j};$
(ii) if
 $L\in {\mathcal{C}}(A;j)$
then
$L\in {\mathcal{C}}(A;j)$
then
 $3L\subset A;$
$3L\subset A;$
(iii) if
 $L,M\in {\mathcal{C}}(A;j)$
are distinct then
$L,M\in {\mathcal{C}}(A;j)$
are distinct then
 $3L\cap 3M=\emptyset ;$
$3L\cap 3M=\emptyset ;$
(iv)
 $7^{-k}{\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A)\leqslant {\mathcal{H}}^{k}(\bigcup _{L\in {\mathcal{C}}(A;j)}L)\leqslant {\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A);$
and
$7^{-k}{\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A)\leqslant {\mathcal{H}}^{k}(\bigcup _{L\in {\mathcal{C}}(A;j)}L)\leqslant {\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A);$
and(v) there exist some constants
 $d_{1},d_{2}>0$
, independent of
$d_{1},d_{2}>0$
, independent of
 $G$
and
$G$
and
 $j$
, such that (21)
$j$
, such that (21) $$\begin{eqnarray}\displaystyle d_{1}\times \biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\leqslant \#{\mathcal{C}}(A;j)\leqslant d_{2}\times \biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{1}\times \biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\leqslant \#{\mathcal{C}}(A;j)\leqslant d_{2}\times \biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}. & & \displaystyle\end{eqnarray}$$
Proof. First of all note that, by the assumption that
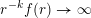 $r^{-k}f(r)\rightarrow \infty$
as
$r^{-k}f(r)\rightarrow \infty$
as
![]() $r\rightarrow 0$
, we have that
$r\rightarrow 0$
, we have that
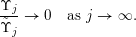 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6F6}_{j}}{\tilde{\unicode[STIX]{x1D6F6}}_{j}}\rightarrow 0\quad \text{as }j\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6F6}_{j}}{\tilde{\unicode[STIX]{x1D6F6}}_{j}}\rightarrow 0\quad \text{as }j\rightarrow \infty .\end{eqnarray}$$
In particular we can assume that
![]() $G$
is sufficiently large so that
$G$
is sufficiently large so that
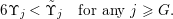 $$\begin{eqnarray}6\unicode[STIX]{x1D6F6}_{j}<\tilde{\unicode[STIX]{x1D6F6}}_{j}\quad \text{for any }j\geqslant G.\end{eqnarray}$$
$$\begin{eqnarray}6\unicode[STIX]{x1D6F6}_{j}<\tilde{\unicode[STIX]{x1D6F6}}_{j}\quad \text{for any }j\geqslant G.\end{eqnarray}$$
Let
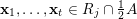 $\mathbf{x}_{1},\ldots ,\mathbf{x}_{t}\in R_{j}\cap \frac{1}{2}A$
be any collection of points such that
$\mathbf{x}_{1},\ldots ,\mathbf{x}_{t}\in R_{j}\cap \frac{1}{2}A$
be any collection of points such that
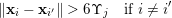 $$\begin{eqnarray}\Vert \mathbf{x}_{i}-\mathbf{x}_{i^{\prime }}\Vert >6\unicode[STIX]{x1D6F6}_{j}\quad \text{if }i\neq i^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\Vert \mathbf{x}_{i}-\mathbf{x}_{i^{\prime }}\Vert >6\unicode[STIX]{x1D6F6}_{j}\quad \text{if }i\neq i^{\prime }\end{eqnarray}$$
and
![]() $t$
is maximal possible. The existence of such a collection follows immediately from the fact that
$t$
is maximal possible. The existence of such a collection follows immediately from the fact that
 $R_{j}\cap \frac{1}{2}A$
is bounded and, by (23), the collection is discrete. Let
$R_{j}\cap \frac{1}{2}A$
is bounded and, by (23), the collection is discrete. Let
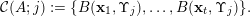 $$\begin{eqnarray}{\mathcal{C}}(A;j):=\{B(\mathbf{x}_{1},\unicode[STIX]{x1D6F6}_{j}),\ldots ,B(\mathbf{x}_{t},\unicode[STIX]{x1D6F6}_{j})\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(A;j):=\{B(\mathbf{x}_{1},\unicode[STIX]{x1D6F6}_{j}),\ldots ,B(\mathbf{x}_{t},\unicode[STIX]{x1D6F6}_{j})\}.\end{eqnarray}$$
Thus, property (i) is trivially satisfied for this collection
![]() ${\mathcal{C}}(A;j)$
. Recall that, by construction,
${\mathcal{C}}(A;j)$
. Recall that, by construction,
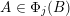 $A\in \unicode[STIX]{x1D6F7}_{j}(B)$
, which means that the radius of
$A\in \unicode[STIX]{x1D6F7}_{j}(B)$
, which means that the radius of
![]() $\frac{1}{2}A$
is
$\frac{1}{2}A$
is
![]() $\frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. If
$\frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. If
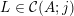 $L\in {\mathcal{C}}(A;j)$
, say
$L\in {\mathcal{C}}(A;j)$
, say
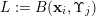 $L:=B(\mathbf{x}_{i},\unicode[STIX]{x1D6F6}_{j})$
, and
$L:=B(\mathbf{x}_{i},\unicode[STIX]{x1D6F6}_{j})$
, and
![]() $A$
is centred at
$A$
is centred at
![]() $\mathbf{x}_{0}$
, then for any
$\mathbf{x}_{0}$
, then for any
![]() $\mathbf{y}\in 3L$
we have that
$\mathbf{y}\in 3L$
we have that
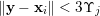 $\Vert \mathbf{y}-\mathbf{x}_{i}\Vert <3\unicode[STIX]{x1D6F6}_{j}$
while
$\Vert \mathbf{y}-\mathbf{x}_{i}\Vert <3\unicode[STIX]{x1D6F6}_{j}$
while
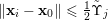 $\Vert \mathbf{x}_{i}-\mathbf{x}_{0}\Vert \leqslant \frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. Then, using (22) and the triangle inequality, we get that
$\Vert \mathbf{x}_{i}-\mathbf{x}_{0}\Vert \leqslant \frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. Then, using (22) and the triangle inequality, we get that
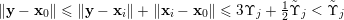 $\Vert \mathbf{y}-\mathbf{x}_{0}\Vert \leqslant \Vert \mathbf{y}-\mathbf{x}_{i}\Vert +\Vert \mathbf{x}_{i}-\mathbf{x}_{0}\Vert \leqslant 3\unicode[STIX]{x1D6F6}_{j}+\frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}<\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. Hence
$\Vert \mathbf{y}-\mathbf{x}_{0}\Vert \leqslant \Vert \mathbf{y}-\mathbf{x}_{i}\Vert +\Vert \mathbf{x}_{i}-\mathbf{x}_{0}\Vert \leqslant 3\unicode[STIX]{x1D6F6}_{j}+\frac{1}{2}\tilde{\unicode[STIX]{x1D6F6}}_{j}<\tilde{\unicode[STIX]{x1D6F6}}_{j}$
. Hence
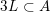 $3L\subset A$
whence property (ii) follows. Further, property (iii) follows immediately from condition (23).
$3L\subset A$
whence property (ii) follows. Further, property (iii) follows immediately from condition (23).
By the maximality of the collection
 $\mathbf{x}_{1},\ldots ,\mathbf{x}_{t}$
, for any
$\mathbf{x}_{1},\ldots ,\mathbf{x}_{t}$
, for any
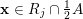 $\mathbf{x}\in R_{j}\cap \frac{1}{2}A$
there exists an
$\mathbf{x}\in R_{j}\cap \frac{1}{2}A$
there exists an
![]() $\mathbf{x}_{i}$
from this collection such that
$\mathbf{x}_{i}$
from this collection such that
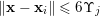 $\Vert \mathbf{x}-\mathbf{x}_{i}\Vert \leqslant 6\unicode[STIX]{x1D6F6}_{j}$
. Hence,
$\Vert \mathbf{x}-\mathbf{x}_{i}\Vert \leqslant 6\unicode[STIX]{x1D6F6}_{j}$
. Hence,
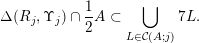 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A\subset \mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}7L.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A\subset \mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}7L.\end{eqnarray}$$
Thus
 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{L\in {\mathcal{C}}(A;j)}{\mathcal{H}}^{k}(7L)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{L\in {\mathcal{C}}(A;j)}7^{k}{\mathcal{H}}^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 7^{k}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}^{\circ }L\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap \frac{1}{2}A\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{L\in {\mathcal{C}}(A;j)}{\mathcal{H}}^{k}(7L)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{L\in {\mathcal{C}}(A;j)}7^{k}{\mathcal{H}}^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 7^{k}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}^{\circ }L\biggr).\nonumber\end{eqnarray}$$
On the other hand, by property (ii), we have that
 $$\begin{eqnarray}\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}^{\circ }L\subset \unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}^{\circ }L\subset \unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A,\end{eqnarray}$$
which together with the previous inequality establishes property (iv).
Finally, property (v) is an immediate consequence of property (iv) upon noting that
 $$\begin{eqnarray}{\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap {\textstyle \frac{1}{2}}A)\asymp {\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A)\asymp \unicode[STIX]{x1D6F6}_{j}^{m}\tilde{\unicode[STIX]{x1D6F6}}_{j}^{l}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap {\textstyle \frac{1}{2}}A)\asymp {\mathcal{H}}^{k}(\unicode[STIX]{x1D6E5}(R_{j},\unicode[STIX]{x1D6F6}_{j})\cap A)\asymp \unicode[STIX]{x1D6F6}_{j}^{m}\tilde{\unicode[STIX]{x1D6F6}}_{j}^{l}\end{eqnarray}$$
and
 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}L\biggr)=\#{\mathcal{C}}(A;j){\mathcal{H}}^{k}(L)\asymp \#{\mathcal{C}}(A;j)\unicode[STIX]{x1D6F6}_{j}^{k},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in {\mathcal{C}}(A;j)}L\biggr)=\#{\mathcal{C}}(A;j){\mathcal{H}}^{k}(L)\asymp \#{\mathcal{C}}(A;j)\unicode[STIX]{x1D6F6}_{j}^{k},\end{eqnarray}$$
where
![]() $l$
is the dimension of
$l$
is the dimension of
![]() $R_{j}$
,
$R_{j}$
,
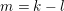 $m=k-l$
and
$m=k-l$
and
![]() $L$
is any ball from
$L$
is any ball from
![]() ${\mathcal{C}}(A;j)$
.◻
${\mathcal{C}}(A;j)$
.◻
Remark.
Throughout we use the Vinogradov notation, writing
![]() $A\ll B$
if
$A\ll B$
if
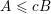 $A\leqslant cB$
for some positive constant
$A\leqslant cB$
for some positive constant
![]() $c$
and
$c$
and
![]() $A\gg B$
if
$A\gg B$
if
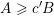 $A\geqslant c^{\prime }B$
for some positive constant
$A\geqslant c^{\prime }B$
for some positive constant
![]() $c^{\prime }$
. If
$c^{\prime }$
. If
![]() $A\ll B$
and
$A\ll B$
and
![]() $A\gg B$
we write
$A\gg B$
we write
![]() $A\asymp B$
.
$A\asymp B$
.
5 Proof of Theorem 1
As with the proof of the mass transference principle given in [Reference Beresnevich and VelaniBV06a] and the proof of Theorem BV1 given in [Reference Beresnevich and VelaniBV06b], we begin by noting that we may assume that
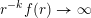 $r^{-k}f(r)\rightarrow \infty$
as
$r^{-k}f(r)\rightarrow \infty$
as
![]() $r\rightarrow 0$
. To see this we first observe that, by Lemma 1, if
$r\rightarrow 0$
. To see this we first observe that, by Lemma 1, if
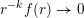 $r^{-k}f(r)\rightarrow 0$
as
$r^{-k}f(r)\rightarrow 0$
as
![]() $r\rightarrow 0$
we have that
$r\rightarrow 0$
we have that
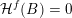 ${\mathcal{H}}^{f}(B)=0$
for any ball
${\mathcal{H}}^{f}(B)=0$
for any ball
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{k}$
. Furthermore, since
$\mathbb{R}^{k}$
. Furthermore, since
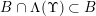 $B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\subset B$
, the result follows trivially.
$B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})\subset B$
, the result follows trivially.
Now suppose that
 $r^{-k}f(r)\rightarrow \unicode[STIX]{x1D706}$
as
$r^{-k}f(r)\rightarrow \unicode[STIX]{x1D706}$
as
![]() $r\rightarrow 0$
for some
$r\rightarrow 0$
for some
 $0<\unicode[STIX]{x1D706}<\infty$
. In this case,
$0<\unicode[STIX]{x1D706}<\infty$
. In this case,
![]() ${\mathcal{H}}^{f}$
is comparable to
${\mathcal{H}}^{f}$
is comparable to
![]() ${\mathcal{H}}^{k}$
and so it would be sufficient to show that
${\mathcal{H}}^{k}$
and so it would be sufficient to show that
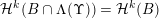 ${\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{k}(B)$
. Since
${\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))={\mathcal{H}}^{k}(B)$
. Since
 $r^{-k}f(r)\rightarrow \unicode[STIX]{x1D706}$
as
$r^{-k}f(r)\rightarrow \unicode[STIX]{x1D706}$
as
![]() $r\rightarrow 0$
we have that the ratio
$r\rightarrow 0$
we have that the ratio
![]() $f(r)/r^{k}$
is bounded between positive constants for sufficiently small
$f(r)/r^{k}$
is bounded between positive constants for sufficiently small
![]() $r$
. In turn, this implies that, in this case, the ratio of the values
$r$
. In turn, this implies that, in this case, the ratio of the values
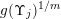 $g(\unicode[STIX]{x1D6F6}_{j})^{1/m}$
and
$g(\unicode[STIX]{x1D6F6}_{j})^{1/m}$
and
![]() $\unicode[STIX]{x1D6F6}_{j}$
is uniformly bounded between positive constants. It then follows from [Reference Beresnevich and VelaniBV08, Lemma 4] that
$\unicode[STIX]{x1D6F6}_{j}$
is uniformly bounded between positive constants. It then follows from [Reference Beresnevich and VelaniBV08, Lemma 4] that
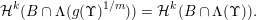 $$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(g(\unicode[STIX]{x1D6F6})^{1/m}))={\mathcal{H}}^{k}(B\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})).\end{eqnarray}$$
This together with (2) then implies the required result in this case.
Thus, for the rest of the proof we may assume without loss of generality that
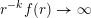 $r^{-k}f(r)\rightarrow \infty$
as
$r^{-k}f(r)\rightarrow \infty$
as
![]() $r\rightarrow 0$
. With this assumption it is a consequence of Lemma 1 that
$r\rightarrow 0$
. With this assumption it is a consequence of Lemma 1 that
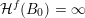 ${\mathcal{H}}^{f}(B_{0})=\infty$
for any ball
${\mathcal{H}}^{f}(B_{0})=\infty$
for any ball
![]() $B_{0}$
in
$B_{0}$
in
![]() $\unicode[STIX]{x1D6FA}$
, which we fix from now on. Therefore, our goal for the rest of the proof is to show that
$\unicode[STIX]{x1D6FA}$
, which we fix from now on. Therefore, our goal for the rest of the proof is to show that
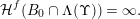 $$\begin{eqnarray}{\mathcal{H}}^{f}(B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))=\infty .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{f}(B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))=\infty .\end{eqnarray}$$
To this end, for each
![]() $\unicode[STIX]{x1D702}>1$
, we will construct a Cantor subset
$\unicode[STIX]{x1D702}>1$
, we will construct a Cantor subset
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
of
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
of
 $B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
and a probability measure
$B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
and a probability measure
![]() $\unicode[STIX]{x1D707}$
supported on
$\unicode[STIX]{x1D707}$
supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
satisfying the condition that for any arbitrary ball
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
satisfying the condition that for any arbitrary ball
![]() $D$
of sufficiently small radius
$D$
of sufficiently small radius
![]() $r(D)$
we have
$r(D)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(D)\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(D)\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}, & & \displaystyle\end{eqnarray}$$
where the implied constant does not depend on
![]() $D$
or
$D$
or
![]() $\unicode[STIX]{x1D702}$
. By the mass distribution principle (Lemma 2) and the fact that
$\unicode[STIX]{x1D702}$
. By the mass distribution principle (Lemma 2) and the fact that
 $\mathbb{K}_{\unicode[STIX]{x1D702}}\subset B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
, we would then have that
$\mathbb{K}_{\unicode[STIX]{x1D702}}\subset B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
, we would then have that
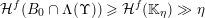 ${\mathcal{H}}^{f}(B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))\geqslant {\mathcal{H}}^{f}(\mathbb{K}_{\unicode[STIX]{x1D702}})\gg \unicode[STIX]{x1D702}$
and the proof is finished by taking
${\mathcal{H}}^{f}(B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6}))\geqslant {\mathcal{H}}^{f}(\mathbb{K}_{\unicode[STIX]{x1D702}})\gg \unicode[STIX]{x1D702}$
and the proof is finished by taking
![]() $\unicode[STIX]{x1D702}$
to be arbitrarily large.
$\unicode[STIX]{x1D702}$
to be arbitrarily large.
5.1 The desired properties of
 $\mathbb{K}_{\unicode[STIX]{x1D702}}$
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
We will construct the Cantor set
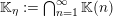 $\mathbb{K}_{\unicode[STIX]{x1D702}}:=\bigcap _{n=1}^{\infty }\mathbb{K}(n)$
so that each level
$\mathbb{K}_{\unicode[STIX]{x1D702}}:=\bigcap _{n=1}^{\infty }\mathbb{K}(n)$
so that each level
![]() $\mathbb{K}(n)$
is a finite union of disjoint closed balls and the levels are nested, that is
$\mathbb{K}(n)$
is a finite union of disjoint closed balls and the levels are nested, that is
 $\mathbb{K}(n)\supset \mathbb{K}(n+1)$
for
$\mathbb{K}(n)\supset \mathbb{K}(n+1)$
for
![]() $n\geqslant 1$
. We will denote the collection of balls constituting level
$n\geqslant 1$
. We will denote the collection of balls constituting level
![]() $n$
by
$n$
by
![]() $K(n)$
. As with the Cantor set in [Reference Beresnevich and VelaniBV06a], the construction of
$K(n)$
. As with the Cantor set in [Reference Beresnevich and VelaniBV06a], the construction of
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
is inductive and each level
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
is inductive and each level
![]() $\mathbb{K}(n)$
will consist of local levels and sub-levels. So, suppose that the
$\mathbb{K}(n)$
will consist of local levels and sub-levels. So, suppose that the
![]() $(n-1)$
th level
$(n-1)$
th level
 $\mathbb{K}(n-1)$
has been constructed. Then, for every
$\mathbb{K}(n-1)$
has been constructed. Then, for every
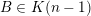 $B\in K(n-1)$
we construct the
$B\in K(n-1)$
we construct the
![]() $(n,B)$
-local level,
$(n,B)$
-local level,
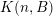 $K(n,B)$
, which will consist of balls contained in
$K(n,B)$
, which will consist of balls contained in
![]() $B$
. The collection of balls
$B$
. The collection of balls
![]() $K(n)$
will take the form
$K(n)$
will take the form
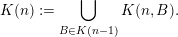 $$\begin{eqnarray}K(n):=\mathop{\bigcup }_{B\in K(n-1)}K(n,B).\end{eqnarray}$$
$$\begin{eqnarray}K(n):=\mathop{\bigcup }_{B\in K(n-1)}K(n,B).\end{eqnarray}$$
Looking even more closely at the construction, each
![]() $(n,B)$
-local level will consist of local sub-levels and will be of the form
$(n,B)$
-local level will consist of local sub-levels and will be of the form
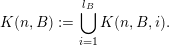 $$\begin{eqnarray}K(n,B):=\mathop{\bigcup }_{i=1}^{l_{B}}K(n,B,i).\end{eqnarray}$$
$$\begin{eqnarray}K(n,B):=\mathop{\bigcup }_{i=1}^{l_{B}}K(n,B,i).\end{eqnarray}$$
Here,
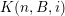 $K(n,B,i)$
denotes the
$K(n,B,i)$
denotes the
![]() $i$
th local sub-level and
$i$
th local sub-level and
![]() $l_{B}$
is the number of local sub-levels. For
$l_{B}$
is the number of local sub-levels. For
![]() $n\geqslant 2$
each local sub-level will be defined as the union
$n\geqslant 2$
each local sub-level will be defined as the union
 $$\begin{eqnarray}K(n,B,i):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,i)}\mathop{\bigcup }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{C}}(A;j),\end{eqnarray}$$
$$\begin{eqnarray}K(n,B,i):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,i)}\mathop{\bigcup }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{C}}(A;j),\end{eqnarray}$$
where
![]() $B^{\prime }$
will lie in a suitably chosen collection of balls
$B^{\prime }$
will lie in a suitably chosen collection of balls
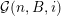 ${\mathcal{G}}(n,B,i)$
within
${\mathcal{G}}(n,B,i)$
within
![]() $B$
,
$B$
,
![]() $K_{G^{\prime },B^{\prime }}$
will arise from Lemma 4 and
$K_{G^{\prime },B^{\prime }}$
will arise from Lemma 4 and
![]() ${\mathcal{C}}(A;j)$
will arise from Lemma 5. It will be apparent from the construction that the parameter
${\mathcal{C}}(A;j)$
will arise from Lemma 5. It will be apparent from the construction that the parameter
![]() $G^{\prime }$
becomes arbitrarily large as we construct levels. The set of all pairs
$G^{\prime }$
becomes arbitrarily large as we construct levels. The set of all pairs
![]() $(A;j)$
that contribute to (26) will be denoted by
$(A;j)$
that contribute to (26) will be denoted by
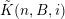 $\tilde{K}(n,B,i)$
. Thus,
$\tilde{K}(n,B,i)$
. Thus,
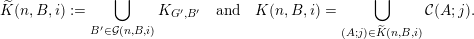 $$\begin{eqnarray}\widetilde{K}(n,B,i):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,i)}K_{G^{\prime },B^{\prime }}\quad \text{and}\quad K(n,B,i)=\mathop{\bigcup }_{(A;j)\in \widetilde{K}(n,B,i)}{\mathcal{C}}(A;j).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{K}(n,B,i):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,i)}K_{G^{\prime },B^{\prime }}\quad \text{and}\quad K(n,B,i)=\mathop{\bigcup }_{(A;j)\in \widetilde{K}(n,B,i)}{\mathcal{C}}(A;j).\end{eqnarray}$$
If additionally we start with
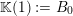 $\mathbb{K}(1):=B_{0}$
then, in view of the definition of the sets
$\mathbb{K}(1):=B_{0}$
then, in view of the definition of the sets
![]() ${\mathcal{C}}(A;j)$
, the inclusion
${\mathcal{C}}(A;j)$
, the inclusion
 $\mathbb{K}_{\unicode[STIX]{x1D702}}\subset B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
is straightforward. Hence the only real part of the proof will be to show the validity of (24) for some suitable measure supported on
$\mathbb{K}_{\unicode[STIX]{x1D702}}\subset B_{0}\cap \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6F6})$
is straightforward. Hence the only real part of the proof will be to show the validity of (24) for some suitable measure supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
. This will require several additional properties which are now stated.
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
. This will require several additional properties which are now stated.
The properties of levels and sub-levels of
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
- (P0)
 $K(1)$
consists of one ball, namely
$K(1)$
consists of one ball, namely
 $B_{0}$
.
$B_{0}$
.- (P1)
For any
 $n\geqslant 2$
and any
$n\geqslant 2$
and any
 $B\in K(n-1)$
the balls
$B\in K(n-1)$
the balls  $$\begin{eqnarray}\{3L:L\in K(n,B)\}\end{eqnarray}$$
$$\begin{eqnarray}\{3L:L\in K(n,B)\}\end{eqnarray}$$
are disjoint and contained in
 $B$
.
$B$
.- (P2)
For any
 $n\geqslant 2$
, any
$n\geqslant 2$
, any
 $B\in K(n-1)$
and any
$B\in K(n-1)$
and any
 $i\in \{1,\ldots ,l_{B}\}$
the local sub-level
$i\in \{1,\ldots ,l_{B}\}$
the local sub-level
 $K(n,B,i)$
is a finite union of some collections
$K(n,B,i)$
is a finite union of some collections
 ${\mathcal{C}}(A;j)$
of balls satisfying properties (i)–(v) of Lemma 5, where the balls
${\mathcal{C}}(A;j)$
of balls satisfying properties (i)–(v) of Lemma 5, where the balls
 $3A$
are disjoint and contained in
$3A$
are disjoint and contained in
 $B$
.
$B$
.- (P3)
For any
 $n\geqslant 2$
,
$n\geqslant 2$
,
 $B\in K(n-1)$
and
$B\in K(n-1)$
and
 $i\in \{1,\ldots ,l_{B}\}$
we have
$i\in \{1,\ldots ,l_{B}\}$
we have  $$\begin{eqnarray}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\geqslant c_{3}V^{k}(B)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\geqslant c_{3}V^{k}(B)\end{eqnarray}$$
where
 $$\begin{eqnarray}c_{3}:=\frac{1}{2^{k+3}\times 5^{k}\times 15^{k}}\bigg(\frac{c_{1}}{c_{2}}\bigg)^{2}\end{eqnarray}$$
$$\begin{eqnarray}c_{3}:=\frac{1}{2^{k+3}\times 5^{k}\times 15^{k}}\bigg(\frac{c_{1}}{c_{2}}\bigg)^{2}\end{eqnarray}$$
with
 $c_{1}$
and
$c_{1}$
and
 $c_{2}$
as defined in (18).
$c_{2}$
as defined in (18).- (P4)
For any
 $n\geqslant 2$
,
$n\geqslant 2$
,
 $B\in K(n-1)$
, any
$B\in K(n-1)$
, any
 $i\in \{1,\ldots ,l_{B}-1\}$
and any
$i\in \{1,\ldots ,l_{B}-1\}$
and any
 $L\in K(n,B,i)$
and
$L\in K(n,B,i)$
and
 $M\in K(n,B,i+1)$
we have
$M\in K(n,B,i+1)$
we have  $$\begin{eqnarray}f(r(M))\leqslant {\textstyle \frac{1}{2}}f(r(L))\quad \text{and}\quad g(r(M))\leqslant {\textstyle \frac{1}{2}}g(r(L)).\end{eqnarray}$$
$$\begin{eqnarray}f(r(M))\leqslant {\textstyle \frac{1}{2}}f(r(L))\quad \text{and}\quad g(r(M))\leqslant {\textstyle \frac{1}{2}}g(r(L)).\end{eqnarray}$$
- (P5)
The number of local sub-levels is defined by
 $$\begin{eqnarray}l_{B}:=\left\{\begin{array}{@{}ll@{}}\displaystyle \biggl[\frac{c_{2}\unicode[STIX]{x1D702}}{c_{3}{\mathcal{H}}^{k}(B)}\biggr]+1 & \text{if }B=B_{0}:=\mathbb{K}(1),\\ \displaystyle \biggl[\frac{V^{f}(B)}{c_{3}V^{k}(B)}\biggr]+1 & \text{if }B\in K(n)\text{ with }n\geqslant 2,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}l_{B}:=\left\{\begin{array}{@{}ll@{}}\displaystyle \biggl[\frac{c_{2}\unicode[STIX]{x1D702}}{c_{3}{\mathcal{H}}^{k}(B)}\biggr]+1 & \text{if }B=B_{0}:=\mathbb{K}(1),\\ \displaystyle \biggl[\frac{V^{f}(B)}{c_{3}V^{k}(B)}\biggr]+1 & \text{if }B\in K(n)\text{ with }n\geqslant 2,\end{array}\right.\end{eqnarray}$$
and satisfies
 $l_{B}\geqslant 2$
for
$l_{B}\geqslant 2$
for
 $B\in K(n)$
with
$B\in K(n)$
with
 $n\geqslant 2$
.
$n\geqslant 2$
.
Properties (P1) and (P2) are imposed to make sure that the balls in the Cantor construction are sufficiently well separated. On the other hand, Properties (P3) and (P5) make sure that there are ‘enough’ balls in each level of the construction of the Cantor set. Property (P4) essentially ensures that all balls involved in the construction of a level of the Cantor set are sufficiently small compared with balls involved in the construction of the previous level. All of the Properties (P1)–(P5) will play a crucial role in the measure estimates we obtain in § 5.4 and § 5.5.
5.2 The existence of
 $\mathbb{K}_{\unicode[STIX]{x1D702}}$
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
In this section we show that it is possible to construct a Cantor set with the properties outlined in § 5.1. In what follows we will use the following notation:
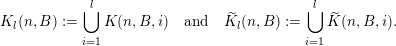 $$\begin{eqnarray}K_{l}(n,B):=\mathop{\bigcup }_{i=1}^{l}K(n,B,i)\quad \text{and}\quad \widetilde{K}_{l}(n,B):=\mathop{\bigcup }_{i=1}^{l}\widetilde{K}(n,B,i).\end{eqnarray}$$
$$\begin{eqnarray}K_{l}(n,B):=\mathop{\bigcup }_{i=1}^{l}K(n,B,i)\quad \text{and}\quad \widetilde{K}_{l}(n,B):=\mathop{\bigcup }_{i=1}^{l}\widetilde{K}(n,B,i).\end{eqnarray}$$
Level 1. The first level is defined by taking the arbitrary ball
![]() $B_{0}$
. Thus,
$B_{0}$
. Thus,
 $\mathbb{K}(1):=B_{0}$
and Property (P0) is trivially satisfied. We proceed by induction. Assume that the first
$\mathbb{K}(1):=B_{0}$
and Property (P0) is trivially satisfied. We proceed by induction. Assume that the first
![]() $(n-1)$
levels
$(n-1)$
levels
![]() $\mathbb{K}(1)$
,
$\mathbb{K}(1)$
,
![]() $\mathbb{K}(2)$
,
$\mathbb{K}(2)$
,
![]() $\ldots$
,
$\ldots$
,
 $\mathbb{K}(n-1)$
have been constructed. We now construct the
$\mathbb{K}(n-1)$
have been constructed. We now construct the
![]() $n$
th level
$n$
th level
![]() $\mathbb{K}(n)$
.
$\mathbb{K}(n)$
.
Level n. To construct the
![]() $n$
th level we will define local levels
$n$
th level we will define local levels
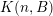 $K(n,B)$
for each
$K(n,B)$
for each
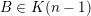 $B\in K(n-1)$
. Therefore, from now on we fix some ball
$B\in K(n-1)$
. Therefore, from now on we fix some ball
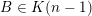 $B\in K(n-1)$
and a sufficiently small constant
$B\in K(n-1)$
and a sufficiently small constant
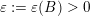 $\unicode[STIX]{x1D700}:=\unicode[STIX]{x1D700}(B)>0$
which will be determined later. Recall that each local level
$\unicode[STIX]{x1D700}:=\unicode[STIX]{x1D700}(B)>0$
which will be determined later. Recall that each local level
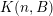 $K(n,B)$
will consist of local sub-levels
$K(n,B)$
will consist of local sub-levels
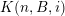 $K(n,B,i)$
where
$K(n,B,i)$
where
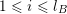 $1\leqslant i\leqslant l_{B}$
and
$1\leqslant i\leqslant l_{B}$
and
![]() $l_{B}$
is given by Property (P5). Let
$l_{B}$
is given by Property (P5). Let
![]() $G\in \mathbb{N}$
be sufficiently large so that Lemmas 4 and 5 are applicable. Furthermore, suppose that
$G\in \mathbb{N}$
be sufficiently large so that Lemmas 4 and 5 are applicable. Furthermore, suppose that
![]() $G$
is large enough so that
$G$
is large enough so that
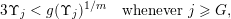 $$\begin{eqnarray}\displaystyle & \displaystyle 3\unicode[STIX]{x1D6F6}_{j}<g(\unicode[STIX]{x1D6F6}_{j})^{1/m}\quad \text{whenever }j\geqslant G, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 3\unicode[STIX]{x1D6F6}_{j}<g(\unicode[STIX]{x1D6F6}_{j})^{1/m}\quad \text{whenever }j\geqslant G, & \displaystyle\end{eqnarray}$$
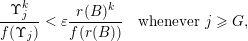 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6F6}_{j}^{k}}{f(\unicode[STIX]{x1D6F6}_{j})}<\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\quad \text{whenever }j\geqslant G, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6F6}_{j}^{k}}{f(\unicode[STIX]{x1D6F6}_{j})}<\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\quad \text{whenever }j\geqslant G, & \displaystyle\end{eqnarray}$$
and
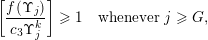 $$\begin{eqnarray}\biggl[\frac{f(\unicode[STIX]{x1D6F6}_{j})}{c_{3}\unicode[STIX]{x1D6F6}_{j}^{k}}\biggr]\geqslant 1\quad \text{whenever }j\geqslant G,\end{eqnarray}$$
$$\begin{eqnarray}\biggl[\frac{f(\unicode[STIX]{x1D6F6}_{j})}{c_{3}\unicode[STIX]{x1D6F6}_{j}^{k}}\biggr]\geqslant 1\quad \text{whenever }j\geqslant G,\end{eqnarray}$$
where
![]() $c_{3}$
is the constant appearing in Property (P3) above. Note that the existence of
$c_{3}$
is the constant appearing in Property (P3) above. Note that the existence of
![]() $G$
satisfying (27)–(29) follows from the assumptions that
$G$
satisfying (27)–(29) follows from the assumptions that
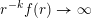 $r^{-k}f(r)\rightarrow \infty$
as
$r^{-k}f(r)\rightarrow \infty$
as
![]() $r\rightarrow 0$
and
$r\rightarrow 0$
and
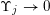 $\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
$\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
![]() $j\rightarrow \infty$
.
$j\rightarrow \infty$
.
Sub-level 1. With
![]() $B$
and
$B$
and
![]() $G$
as above, let
$G$
as above, let
![]() $K_{G,B}$
denote the collection of balls arising from Lemma 4. Define the first sub-level of
$K_{G,B}$
denote the collection of balls arising from Lemma 4. Define the first sub-level of
 $K(n,B)$
to be
$K(n,B)$
to be
 $$\begin{eqnarray}K(n,B,1):=\mathop{\bigcup }_{(A;j)\in K_{G,B}}{\mathcal{C}}(A;j),\end{eqnarray}$$
$$\begin{eqnarray}K(n,B,1):=\mathop{\bigcup }_{(A;j)\in K_{G,B}}{\mathcal{C}}(A;j),\end{eqnarray}$$
thus
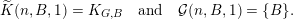 $$\begin{eqnarray}\widetilde{K}(n,B,1)=K_{G,B}\quad \text{and}\quad {\mathcal{G}}(n,B,1)=\{B\}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{K}(n,B,1)=K_{G,B}\quad \text{and}\quad {\mathcal{G}}(n,B,1)=\{B\}.\end{eqnarray}$$
By the properties of
![]() ${\mathcal{C}}(A;j)$
(Lemma 5), it follows that (P1) is satisfied within this sub-level. From the properties of
${\mathcal{C}}(A;j)$
(Lemma 5), it follows that (P1) is satisfied within this sub-level. From the properties of
![]() $K_{G,B}$
(Lemma 4) and Lemma 5 it follows that (P2) and (P3) are satisfied for
$K_{G,B}$
(Lemma 4) and Lemma 5 it follows that (P2) and (P3) are satisfied for
![]() $i=1$
.
$i=1$
.
Higher sub-levels. To construct higher sub-levels we argue by induction. For
![]() $l<l_{B}$
, assume that the sub-levels
$l<l_{B}$
, assume that the sub-levels
 $K(n,B,1),\ldots ,K(n,B,l)$
satisfying Properties (P1)–(P4) with
$K(n,B,1),\ldots ,K(n,B,l)$
satisfying Properties (P1)–(P4) with
![]() $l_{B}$
replaced by
$l_{B}$
replaced by
![]() $l$
have already been defined. We now construct the next sub-level
$l$
have already been defined. We now construct the next sub-level
 $K(n,B,l+1)$
.
$K(n,B,l+1)$
.
As every sub-level of the construction has to be well separated from the previous ones, we first verify that there is enough ‘space’ left over in
![]() $B$
once we have removed the sub-levels
$B$
once we have removed the sub-levels
 $K(n,B,1),\ldots ,K(n,B,l)$
from
$K(n,B,1),\ldots ,K(n,B,l)$
from
![]() $B$
. More precisely, let
$B$
. More precisely, let
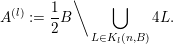 $$\begin{eqnarray}A^{(l)}:=\frac{1}{2}B\bigg\backslash\mathop{\bigcup }_{L\in K_{l}(n,B)}4L.\end{eqnarray}$$
$$\begin{eqnarray}A^{(l)}:=\frac{1}{2}B\bigg\backslash\mathop{\bigcup }_{L\in K_{l}(n,B)}4L.\end{eqnarray}$$
We will show that
 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}(A^{(l)})\geqslant {\textstyle \frac{1}{2}}{\mathcal{H}}^{k}({\textstyle \frac{1}{2}}B). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}(A^{(l)})\geqslant {\textstyle \frac{1}{2}}{\mathcal{H}}^{k}({\textstyle \frac{1}{2}}B). & & \displaystyle\end{eqnarray}$$
First, observe that
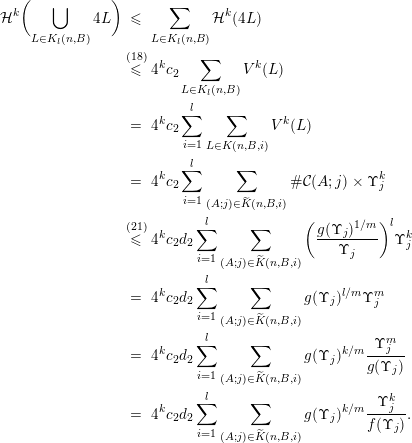 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{L\in K_{l}(n,B)}{\mathcal{H}}^{k}(4L)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 4^{k}c_{2}\mathop{\sum }_{L\in K_{l}(n,B)}V^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{L\in K(n,B,i)}V^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\#{\mathcal{C}}(A;j)\times \unicode[STIX]{x1D6F6}_{j}^{k}\nonumber\\ \displaystyle & \stackrel{(21)}{{\leqslant}} & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\unicode[STIX]{x1D6F6}_{j}^{k}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{l/m}\unicode[STIX]{x1D6F6}_{j}^{m}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\frac{\unicode[STIX]{x1D6F6}_{j}^{m}}{g(\unicode[STIX]{x1D6F6}_{j})}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\frac{\unicode[STIX]{x1D6F6}_{j}^{k}}{f(\unicode[STIX]{x1D6F6}_{j})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{L\in K_{l}(n,B)}{\mathcal{H}}^{k}(4L)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 4^{k}c_{2}\mathop{\sum }_{L\in K_{l}(n,B)}V^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{L\in K(n,B,i)}V^{k}(L)\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\#{\mathcal{C}}(A;j)\times \unicode[STIX]{x1D6F6}_{j}^{k}\nonumber\\ \displaystyle & \stackrel{(21)}{{\leqslant}} & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\unicode[STIX]{x1D6F6}_{j}^{k}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{l/m}\unicode[STIX]{x1D6F6}_{j}^{m}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\frac{\unicode[STIX]{x1D6F6}_{j}^{m}}{g(\unicode[STIX]{x1D6F6}_{j})}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\frac{\unicode[STIX]{x1D6F6}_{j}^{k}}{f(\unicode[STIX]{x1D6F6}_{j})}.\nonumber\end{eqnarray}$$
Hence, by (28), we get that
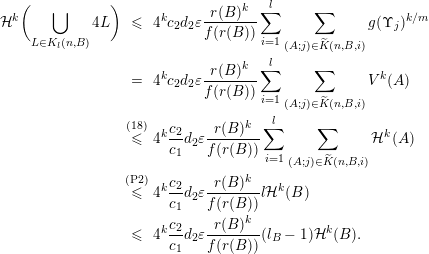 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr) & {\leqslant} & \displaystyle 4^{k}c_{2}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}2)}{{\leqslant}} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}l{\mathcal{H}}^{k}(B)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}(l_{B}-1){\mathcal{H}}^{k}(B).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr) & {\leqslant} & \displaystyle 4^{k}c_{2}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}\nonumber\\ \displaystyle & = & \displaystyle 4^{k}c_{2}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}\mathop{\sum }_{i=1}^{l}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}2)}{{\leqslant}} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}l{\mathcal{H}}^{k}(B)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 4^{k}\frac{c_{2}}{c_{1}}d_{2}\unicode[STIX]{x1D700}\frac{r(B)^{k}}{f(r(B))}(l_{B}-1){\mathcal{H}}^{k}(B).\end{eqnarray}$$
If
![]() $B=B_{0}$
, set
$B=B_{0}$
, set
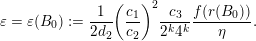 $$\begin{eqnarray}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(B_{0}):=\frac{1}{2d_{2}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}\frac{c_{3}}{2^{k}4^{k}}\frac{f(r(B_{0}))}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(B_{0}):=\frac{1}{2d_{2}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}\frac{c_{3}}{2^{k}4^{k}}\frac{f(r(B_{0}))}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Otherwise, if
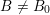 $B\neq B_{0}$
, set
$B\neq B_{0}$
, set
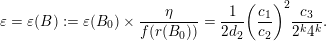 $$\begin{eqnarray}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(B):=\unicode[STIX]{x1D700}(B_{0})\times \frac{\unicode[STIX]{x1D702}}{f(r(B_{0}))}=\frac{1}{2d_{2}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}\frac{c_{3}}{2^{k}4^{k}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(B):=\unicode[STIX]{x1D700}(B_{0})\times \frac{\unicode[STIX]{x1D702}}{f(r(B_{0}))}=\frac{1}{2d_{2}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}\frac{c_{3}}{2^{k}4^{k}}.\end{eqnarray}$$
Then, it follows from (31) combined with (P5) that
 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr)\leqslant \frac{1}{2}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{L\in K_{l}(n,B)}4L\biggr)\leqslant \frac{1}{2}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr),\end{eqnarray}$$
thus verifying (30).
By construction,
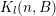 $K_{l}(n,B)$
is a finite collection of balls. Therefore, the quantity
$K_{l}(n,B)$
is a finite collection of balls. Therefore, the quantity
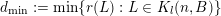 $$\begin{eqnarray}d_{\min }:=\min \{r(L):L\in K_{l}(n,B)\}\end{eqnarray}$$
$$\begin{eqnarray}d_{\min }:=\min \{r(L):L\in K_{l}(n,B)\}\end{eqnarray}$$
is well defined and positive. Let
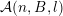 ${\mathcal{A}}(n,B,l)$
be the collection of all the balls of diameter
${\mathcal{A}}(n,B,l)$
be the collection of all the balls of diameter
![]() $d_{\min }$
centred at a point in
$d_{\min }$
centred at a point in
![]() $A^{(l)}$
. By the
$A^{(l)}$
. By the
![]() $5r$
-covering lemma (Lemma 3), there exists a disjoint subcollection
$5r$
-covering lemma (Lemma 3), there exists a disjoint subcollection
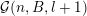 ${\mathcal{G}}(n,B,l+1)$
of
${\mathcal{G}}(n,B,l+1)$
of
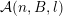 ${\mathcal{A}}(n,B,l)$
such that
${\mathcal{A}}(n,B,l)$
such that
 $$\begin{eqnarray}A^{(l)}\subset \mathop{\bigcup }_{B^{\prime }\in {\mathcal{A}}(n,B,l)}B^{\prime }\subset \mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}A^{(l)}\subset \mathop{\bigcup }_{B^{\prime }\in {\mathcal{A}}(n,B,l)}B^{\prime }\subset \mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }.\end{eqnarray}$$
The collection
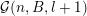 ${\mathcal{G}}(n,B,l+1)$
is clearly contained within
${\mathcal{G}}(n,B,l+1)$
is clearly contained within
![]() $B$
and, since the balls in this collection are disjoint and of the same size, it is finite. Moreover, by construction
$B$
and, since the balls in this collection are disjoint and of the same size, it is finite. Moreover, by construction
 $$\begin{eqnarray}B^{\prime }\cap \mathop{\bigcup }_{L\in K_{l}(n,B)}3L=\emptyset \quad \text{for any }B^{\prime }\in {\mathcal{G}}(n,B,l+1);\end{eqnarray}$$
$$\begin{eqnarray}B^{\prime }\cap \mathop{\bigcup }_{L\in K_{l}(n,B)}3L=\emptyset \quad \text{for any }B^{\prime }\in {\mathcal{G}}(n,B,l+1);\end{eqnarray}$$
i.e. the balls in
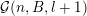 ${\mathcal{G}}(n,B,l+1)$
do not intersect any of the
${\mathcal{G}}(n,B,l+1)$
do not intersect any of the
![]() $3L$
balls from the previous sub-levels. It follows that
$3L$
balls from the previous sub-levels. It follows that
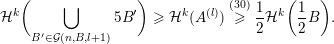 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }\biggr)\geqslant {\mathcal{H}}^{k}(A^{(l)})\stackrel{(30)}{{\geqslant}}\frac{1}{2}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }\biggr)\geqslant {\mathcal{H}}^{k}(A^{(l)})\stackrel{(30)}{{\geqslant}}\frac{1}{2}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr).\end{eqnarray}$$
On the other hand, since
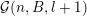 ${\mathcal{G}}(n,B,l+1)$
is a disjoint collection of balls we have that
${\mathcal{G}}(n,B,l+1)$
is a disjoint collection of balls we have that
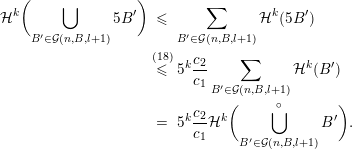 $$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}{\mathcal{H}}^{k}(5B^{\prime })\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 5^{k}\frac{c_{2}}{c_{1}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}{\mathcal{H}}^{k}(B^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 5^{k}\frac{c_{2}}{c_{1}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}^{\circ }B^{\prime }\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}5B^{\prime }\biggr) & {\leqslant} & \displaystyle \mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}{\mathcal{H}}^{k}(5B^{\prime })\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle 5^{k}\frac{c_{2}}{c_{1}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}{\mathcal{H}}^{k}(B^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 5^{k}\frac{c_{2}}{c_{1}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}^{\circ }B^{\prime }\biggr).\nonumber\end{eqnarray}$$
Hence,
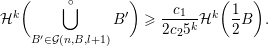 $$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}^{\circ }B^{\prime }\biggr)\geqslant \frac{c_{1}}{2c_{2}5^{k}}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}^{\circ }B^{\prime }\biggr)\geqslant \frac{c_{1}}{2c_{2}5^{k}}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr).\end{eqnarray}$$
Now we are ready to construct the
![]() $(l+1)$
th sub-level
$(l+1)$
th sub-level
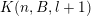 $K(n,B,l+1)$
. Let
$K(n,B,l+1)$
. Let
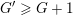 $G^{\prime }\geqslant G+1$
be sufficiently large so that Lemmas 4 and 5 are applicable to every ball
$G^{\prime }\geqslant G+1$
be sufficiently large so that Lemmas 4 and 5 are applicable to every ball
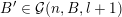 $B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
with
$B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
with
![]() $G^{\prime }$
in place of
$G^{\prime }$
in place of
![]() $G$
. Furthermore, ensure that
$G$
. Furthermore, ensure that
![]() $G^{\prime }$
is sufficiently large so that for every
$G^{\prime }$
is sufficiently large so that for every
![]() $i\geqslant G^{\prime }$
,
$i\geqslant G^{\prime }$
,
 $$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D6F6}_{i})\leqslant {\textstyle \frac{1}{2}}\min _{L\in K_{l}(n,B)}f(r(L))\quad \text{and}\quad g(\unicode[STIX]{x1D6F6}_{i})\leqslant {\textstyle \frac{1}{2}}\min _{L\in K_{l}(n,B)}g(r(L)). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D6F6}_{i})\leqslant {\textstyle \frac{1}{2}}\min _{L\in K_{l}(n,B)}f(r(L))\quad \text{and}\quad g(\unicode[STIX]{x1D6F6}_{i})\leqslant {\textstyle \frac{1}{2}}\min _{L\in K_{l}(n,B)}g(r(L)). & & \displaystyle\end{eqnarray}$$
Imposing the above assumptions on
![]() $G^{\prime }$
is possible since there are only finitely many balls in
$G^{\prime }$
is possible since there are only finitely many balls in
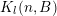 $K_{l}(n,B)$
,
$K_{l}(n,B)$
,
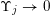 $\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
$\unicode[STIX]{x1D6F6}_{j}\rightarrow 0$
as
![]() $j\rightarrow \infty$
, and
$j\rightarrow \infty$
, and
![]() $f$
and
$f$
and
![]() $g$
are dimension functions.
$g$
are dimension functions.
Now, to each ball
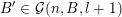 $B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
we apply Lemma 4 to obtain a collection of balls
$B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
we apply Lemma 4 to obtain a collection of balls
![]() $K_{G^{\prime },B^{\prime }}$
and define
$K_{G^{\prime },B^{\prime }}$
and define
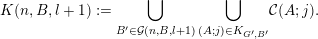 $$\begin{eqnarray}K(n,B,l+1):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\bigcup }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{C}}(A;j).\end{eqnarray}$$
$$\begin{eqnarray}K(n,B,l+1):=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\bigcup }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{C}}(A;j).\end{eqnarray}$$
Consequently,
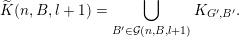 $$\begin{eqnarray}\widetilde{K}(n,B,l+1)=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}K_{G^{\prime },B^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{K}(n,B,l+1)=\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}K_{G^{\prime },B^{\prime }}.\end{eqnarray}$$
Since
![]() $G^{\prime }\geqslant G$
, properties (27)–(29) remain valid. We now verify Properties (P1)–(P5) for this sub-level.
$G^{\prime }\geqslant G$
, properties (27)–(29) remain valid. We now verify Properties (P1)–(P5) for this sub-level.
Regarding (P1), we first observe that it is satisfied for balls in
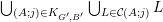 $\bigcup _{(A;j)\in K_{G^{\prime },B^{\prime }}}\bigcup _{L\in {\mathcal{C}}(A;j)}L$
by the properties of
$\bigcup _{(A;j)\in K_{G^{\prime },B^{\prime }}}\bigcup _{L\in {\mathcal{C}}(A;j)}L$
by the properties of
![]() ${\mathcal{C}}(A;j)$
and the fact that the balls in
${\mathcal{C}}(A;j)$
and the fact that the balls in
![]() $K_{G^{\prime },B^{\prime }}$
are disjoint. Next, since any balls in
$K_{G^{\prime },B^{\prime }}$
are disjoint. Next, since any balls in
![]() $K_{G^{\prime },B^{\prime }}$
are contained in
$K_{G^{\prime },B^{\prime }}$
are contained in
![]() $B^{\prime }$
and the balls
$B^{\prime }$
and the balls
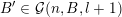 $B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
are disjoint, it follows that (P1) is satisfied for balls
$B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
are disjoint, it follows that (P1) is satisfied for balls
![]() $L$
in
$L$
in
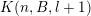 $K(n,B,l+1)$
. Finally, combining this with (32), we see that (P1) is satisfied for balls
$K(n,B,l+1)$
. Finally, combining this with (32), we see that (P1) is satisfied for balls
![]() $L$
in
$L$
in
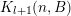 $K_{l+1}(n,B)$
. That (P2) is satisfied for this sub-level is a consequence of Lemma 4(i) and (ii) and the fact that the balls
$K_{l+1}(n,B)$
. That (P2) is satisfied for this sub-level is a consequence of Lemma 4(i) and (ii) and the fact that the balls
 $B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
are disjoint.
$B^{\prime }\in {\mathcal{G}}(n,B,l+1)$
are disjoint.
To establish (P3) for
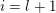 $i=l+1$
note that
$i=l+1$
note that
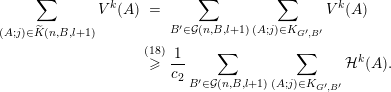 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,l+1)}V^{k}(A) & = & \displaystyle \mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\sum }_{(A;j)\in K_{G^{\prime },B^{\prime }}}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle \frac{1}{c_{2}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\sum }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{H}}^{k}(A).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,l+1)}V^{k}(A) & = & \displaystyle \mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\sum }_{(A;j)\in K_{G^{\prime },B^{\prime }}}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle \frac{1}{c_{2}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\mathop{\sum }_{(A;j)\in K_{G^{\prime },B^{\prime }}}{\mathcal{H}}^{k}(A).\nonumber\end{eqnarray}$$
Then, by Lemma 4 and the disjointness of the balls in
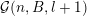 ${\mathcal{G}}(n,B,l+1)$
, we have that
${\mathcal{G}}(n,B,l+1)$
, we have that
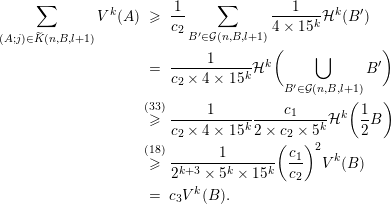 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,l+1)}V^{k}(A) & {\geqslant} & \displaystyle \frac{1}{c_{2}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{c_{2}\times 4\times 15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}B^{\prime }\biggr)\nonumber\\ \displaystyle & \stackrel{(33)}{{\geqslant}} & \displaystyle \frac{1}{c_{2}\times 4\times 15^{k}}\frac{c_{1}}{2\times c_{2}\times 5^{k}}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr)\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle \frac{1}{2^{k+3}\times 5^{k}\times 15^{k}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle c_{3}V^{k}(B).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,l+1)}V^{k}(A) & {\geqslant} & \displaystyle \frac{1}{c_{2}}\mathop{\sum }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}\frac{1}{4\times 15^{k}}{\mathcal{H}}^{k}(B^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{c_{2}\times 4\times 15^{k}}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{B^{\prime }\in {\mathcal{G}}(n,B,l+1)}B^{\prime }\biggr)\nonumber\\ \displaystyle & \stackrel{(33)}{{\geqslant}} & \displaystyle \frac{1}{c_{2}\times 4\times 15^{k}}\frac{c_{1}}{2\times c_{2}\times 5^{k}}{\mathcal{H}}^{k}\biggl(\frac{1}{2}B\biggr)\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle \frac{1}{2^{k+3}\times 5^{k}\times 15^{k}}\biggl(\frac{c_{1}}{c_{2}}\biggr)^{2}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle c_{3}V^{k}(B).\nonumber\end{eqnarray}$$
Finally, (P4) is trivially satisfied as a consequence of the imposed condition (34) and (P5), that
![]() $l_{L}\geqslant 2$
for any ball
$l_{L}\geqslant 2$
for any ball
![]() $L$
in
$L$
in
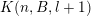 $K(n,B,l+1)$
, follows from (29).
$K(n,B,l+1)$
, follows from (29).
Hence, Properties (P1)–(P5) are satisfied up to the local sub-level
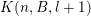 $K(n,B,l+1)$
thus establishing the existence of the local level
$K(n,B,l+1)$
thus establishing the existence of the local level
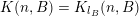 $K(n,B)=K_{l_{B}}(n,B)$
for each
$K(n,B)=K_{l_{B}}(n,B)$
for each
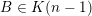 $B\in K(n-1)$
. In turn, this establishes the existence of the
$B\in K(n-1)$
. In turn, this establishes the existence of the
![]() $n$
th level
$n$
th level
![]() $K(n)$
(and also
$K(n)$
(and also
![]() $\mathbb{K}(n)$
).
$\mathbb{K}(n)$
).
5.3 The measure
 $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
 $\mathbb{K}_{\unicode[STIX]{x1D702}}$
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
In this section, we define a probability measure
![]() $\unicode[STIX]{x1D707}$
supported on
$\unicode[STIX]{x1D707}$
supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
. We will eventually show that the measure satisfies (24). For any ball
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
. We will eventually show that the measure satisfies (24). For any ball
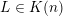 $L\in K(n)$
, we attach a weight
$L\in K(n)$
, we attach a weight
![]() $\unicode[STIX]{x1D707}(L)$
defined recursively as follows.
$\unicode[STIX]{x1D707}(L)$
defined recursively as follows.
For
![]() $n=1$
, we have that
$n=1$
, we have that
 $L=B_{0}:=\mathbb{K}(1)$
and we set
$L=B_{0}:=\mathbb{K}(1)$
and we set
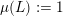 $\unicode[STIX]{x1D707}(L):=1$
. For subsequent levels the measure is defined inductively.
$\unicode[STIX]{x1D707}(L):=1$
. For subsequent levels the measure is defined inductively.
Let
![]() $n\geqslant 2$
and suppose that
$n\geqslant 2$
and suppose that
![]() $\unicode[STIX]{x1D707}(B)$
is defined for every
$\unicode[STIX]{x1D707}(B)$
is defined for every
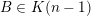 $B\in K(n-1)$
. In particular, we have that
$B\in K(n-1)$
. In particular, we have that
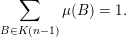 $$\begin{eqnarray}\mathop{\sum }_{B\in K(n-1)}\unicode[STIX]{x1D707}(B)=1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{B\in K(n-1)}\unicode[STIX]{x1D707}(B)=1.\end{eqnarray}$$
Let
![]() $L$
be a ball in
$L$
be a ball in
![]() $K(n)$
. By construction, there is a unique ball
$K(n)$
. By construction, there is a unique ball
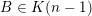 $B\in K(n-1)$
such that
$B\in K(n-1)$
such that
![]() $L\subset B$
. Recall, by (25) and (26), that
$L\subset B$
. Recall, by (25) and (26), that
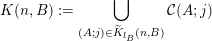 $$\begin{eqnarray}K(n,B):=\mathop{\bigcup }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}{\mathcal{C}}(A;j)\end{eqnarray}$$
$$\begin{eqnarray}K(n,B):=\mathop{\bigcup }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}{\mathcal{C}}(A;j)\end{eqnarray}$$
and so
![]() $L$
is an element of one of the collections
$L$
is an element of one of the collections
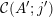 ${\mathcal{C}}(A^{\prime };j^{\prime })$
appearing in the right-hand side of the above. We therefore define
${\mathcal{C}}(A^{\prime };j^{\prime })$
appearing in the right-hand side of the above. We therefore define
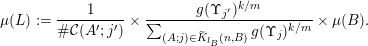 $$\begin{eqnarray}\unicode[STIX]{x1D707}(L):=\frac{1}{\#{\mathcal{C}}(A^{\prime };j^{\prime })}\times \frac{g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{k/m}}{\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(L):=\frac{1}{\#{\mathcal{C}}(A^{\prime };j^{\prime })}\times \frac{g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{k/m}}{\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B).\end{eqnarray}$$
Thus
![]() $\unicode[STIX]{x1D707}$
is inductively defined on any ball appearing in the construction of
$\unicode[STIX]{x1D707}$
is inductively defined on any ball appearing in the construction of
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Furthermore,
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Furthermore,
![]() $\unicode[STIX]{x1D707}$
can be uniquely extended in a standard way to all Borel subsets
$\unicode[STIX]{x1D707}$
can be uniquely extended in a standard way to all Borel subsets
![]() $F$
of
$F$
of
![]() $\mathbb{R}^{k}$
to give a probability measure
$\mathbb{R}^{k}$
to give a probability measure
![]() $\unicode[STIX]{x1D707}$
supported on
$\unicode[STIX]{x1D707}$
supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Indeed, for any Borel subset
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Indeed, for any Borel subset
![]() $F$
of
$F$
of
![]() $\mathbb{R}^{k}$
,
$\mathbb{R}^{k}$
,
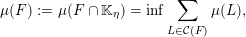 $$\begin{eqnarray}\unicode[STIX]{x1D707}(F):=\unicode[STIX]{x1D707}(F\cap \mathbb{K}_{\unicode[STIX]{x1D702}})=\inf \mathop{\sum }_{L\in {\mathcal{C}}(F)}\unicode[STIX]{x1D707}(L),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(F):=\unicode[STIX]{x1D707}(F\cap \mathbb{K}_{\unicode[STIX]{x1D702}})=\inf \mathop{\sum }_{L\in {\mathcal{C}}(F)}\unicode[STIX]{x1D707}(L),\end{eqnarray}$$
where the infimum is taken over all covers
![]() ${\mathcal{C}}(F)$
of
${\mathcal{C}}(F)$
of
![]() $F\cap \mathbb{K}_{\unicode[STIX]{x1D702}}$
by balls
$F\cap \mathbb{K}_{\unicode[STIX]{x1D702}}$
by balls
 $L\in \bigcup _{n\in \mathbb{N}}K(n)$
. See [Reference FalconerFal03, Proposition 1.7] for further details.
$L\in \bigcup _{n\in \mathbb{N}}K(n)$
. See [Reference FalconerFal03, Proposition 1.7] for further details.
We end this section by observing that
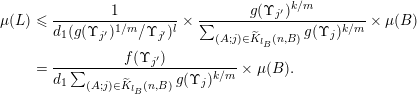 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L) & {\leqslant} & \displaystyle \frac{1}{d_{1}(g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{1/m}/\unicode[STIX]{x1D6F6}_{j^{\prime }})^{l}}\times \frac{g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{k/m}}{\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B)\nonumber\\ \displaystyle & = & \displaystyle \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L) & {\leqslant} & \displaystyle \frac{1}{d_{1}(g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{1/m}/\unicode[STIX]{x1D6F6}_{j^{\prime }})^{l}}\times \frac{g(\unicode[STIX]{x1D6F6}_{j^{\prime }})^{k/m}}{\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B)\nonumber\\ \displaystyle & = & \displaystyle \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \unicode[STIX]{x1D707}(B).\end{eqnarray}$$
This is a consequence of (21) and the relationship between
![]() $f$
and
$f$
and
![]() $g$
. In fact, the above inequality can be reversed if
$g$
. In fact, the above inequality can be reversed if
![]() $d_{1}$
is replaced by
$d_{1}$
is replaced by
![]() $d_{2}$
.
$d_{2}$
.
5.4 The measure of a ball in the Cantor set construction
The goal of this section is to prove that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\ll \frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\ll \frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & & \displaystyle\end{eqnarray}$$
for any ball
![]() $L$
in
$L$
in
![]() $K(n)$
with
$K(n)$
with
![]() $n\geqslant 2$
. We will begin with the level
$n\geqslant 2$
. We will begin with the level
![]() $n=2$
. Fix any ball
$n=2$
. Fix any ball
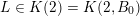 $L\in K(2)=K(2,B_{0})$
. Further, let
$L\in K(2)=K(2,B_{0})$
. Further, let
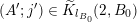 $(A^{\prime };j^{\prime })\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})$
be such that
$(A^{\prime };j^{\prime })\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})$
be such that
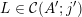 $L\in {\mathcal{C}}(A^{\prime };j^{\prime })$
. Then, by (35), the definition of
$L\in {\mathcal{C}}(A^{\prime };j^{\prime })$
. Then, by (35), the definition of
![]() $\unicode[STIX]{x1D707}$
and the fact that
$\unicode[STIX]{x1D707}$
and the fact that
 $\unicode[STIX]{x1D707}(B_{0})=1$
, we have that
$\unicode[STIX]{x1D707}(B_{0})=1$
, we have that
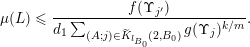 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\leqslant \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\leqslant \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}. & & \displaystyle\end{eqnarray}$$
Next, by Properties (P3) and (P5) of the Cantor set construction, we get that
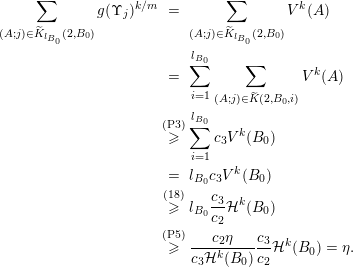 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}g(\unicode[STIX]{x1D6F6}_{j})^{k/m} & = & \displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}V^{k}(A)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B_{0}}}\mathop{\sum }_{(A;j)\in \widetilde{K}(2,B_{0},i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}3)}{{\geqslant}} & \displaystyle \mathop{\sum }_{i=1}^{l_{B_{0}}}c_{3}V^{k}(B_{0})\nonumber\\ \displaystyle & = & \displaystyle l_{B_{0}}c_{3}V^{k}(B_{0})\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle l_{B_{0}}\frac{c_{3}}{c_{2}}{\mathcal{H}}^{k}(B_{0})\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\geqslant}} & \displaystyle \frac{c_{2}\unicode[STIX]{x1D702}}{c_{3}{\mathcal{H}}^{k}(B_{0})}\frac{c_{3}}{c_{2}}{\mathcal{H}}^{k}(B_{0})=\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}g(\unicode[STIX]{x1D6F6}_{j})^{k/m} & = & \displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B_{0}}}(2,B_{0})}V^{k}(A)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B_{0}}}\mathop{\sum }_{(A;j)\in \widetilde{K}(2,B_{0},i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}3)}{{\geqslant}} & \displaystyle \mathop{\sum }_{i=1}^{l_{B_{0}}}c_{3}V^{k}(B_{0})\nonumber\\ \displaystyle & = & \displaystyle l_{B_{0}}c_{3}V^{k}(B_{0})\nonumber\\ \displaystyle & \stackrel{(18)}{{\geqslant}} & \displaystyle l_{B_{0}}\frac{c_{3}}{c_{2}}{\mathcal{H}}^{k}(B_{0})\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\geqslant}} & \displaystyle \frac{c_{2}\unicode[STIX]{x1D702}}{c_{3}{\mathcal{H}}^{k}(B_{0})}\frac{c_{3}}{c_{2}}{\mathcal{H}}^{k}(B_{0})=\unicode[STIX]{x1D702}.\end{eqnarray}$$
Combining (37) and (38) gives (36) as required since
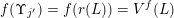 $f(\unicode[STIX]{x1D6F6}_{j^{\prime }})=f(r(L))=V^{f}(L)$
.
$f(\unicode[STIX]{x1D6F6}_{j^{\prime }})=f(r(L))=V^{f}(L)$
.
Now let
![]() $n>2$
and assume that (36) holds for balls in
$n>2$
and assume that (36) holds for balls in
 $K(n-1)$
. Consider an arbitrary ball
$K(n-1)$
. Consider an arbitrary ball
![]() $L$
in
$L$
in
![]() $K(n)$
. Then there exists a unique ball
$K(n)$
. Then there exists a unique ball
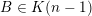 $B\in K(n-1)$
such that
$B\in K(n-1)$
such that
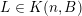 $L\in K(n,B)$
. Further, let
$L\in K(n,B)$
. Further, let
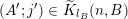 $(A^{\prime };j^{\prime })\in \widetilde{K}_{l_{B}}(n,B)$
be such that
$(A^{\prime };j^{\prime })\in \widetilde{K}_{l_{B}}(n,B)$
be such that
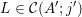 $L\in {\mathcal{C}}(A^{\prime };j^{\prime })$
. Then it follows from (35) and our induction hypothesis that
$L\in {\mathcal{C}}(A^{\prime };j^{\prime })$
. Then it follows from (35) and our induction hypothesis that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\ll \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \frac{V^{f}(B)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(L)\ll \frac{f(\unicode[STIX]{x1D6F6}_{j^{\prime }})}{d_{1}\mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}\times \frac{V^{f}(B)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
Now, we have that
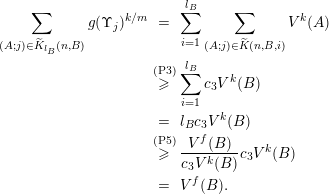 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m} & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}3)}{{\geqslant}} & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}c_{3}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle l_{B}c_{3}V^{k}(B)\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\geqslant}} & \displaystyle \frac{V^{f}(B)}{c_{3}V^{k}(B)}c_{3}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle V^{f}(B).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{(A;j)\in \widetilde{K}_{l_{B}}(n,B)}g(\unicode[STIX]{x1D6F6}_{j})^{k/m} & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}V^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}3)}{{\geqslant}} & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}c_{3}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle l_{B}c_{3}V^{k}(B)\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\geqslant}} & \displaystyle \frac{V^{f}(B)}{c_{3}V^{k}(B)}c_{3}V^{k}(B)\nonumber\\ \displaystyle & = & \displaystyle V^{f}(B).\end{eqnarray}$$
Since
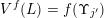 $V^{f}(L)=f(\unicode[STIX]{x1D6F6}_{j^{\prime }})$
, combining (39) and (40) gives (36) and thus completes the proof of this section.
$V^{f}(L)=f(\unicode[STIX]{x1D6F6}_{j^{\prime }})$
, combining (39) and (40) gives (36) and thus completes the proof of this section.
5.5 The measure of an arbitrary ball
Set
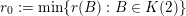 $r_{0}:=\min \{r(B):B\in K(2)\}$
. Take an arbitrary ball
$r_{0}:=\min \{r(B):B\in K(2)\}$
. Take an arbitrary ball
![]() $D$
such that
$D$
such that
 $r(D)<r_{0}$
. We wish to establish (24) for
$r(D)<r_{0}$
. We wish to establish (24) for
![]() $D$
, i.e. we wish to show that
$D$
, i.e. we wish to show that
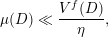 $$\begin{eqnarray}\unicode[STIX]{x1D707}(D)\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(D)\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}},\end{eqnarray}$$
where the implied constant is independent of
![]() $D$
and
$D$
and
![]() $\unicode[STIX]{x1D702}$
. In accomplishing this goal the following lemma from [Reference Beresnevich and VelaniBV06a] will be useful.
$\unicode[STIX]{x1D702}$
. In accomplishing this goal the following lemma from [Reference Beresnevich and VelaniBV06a] will be useful.
Lemma 6. Let
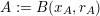 $A:=B(x_{A},r_{A})$
and
$A:=B(x_{A},r_{A})$
and
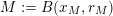 $M:=B(x_{M},r_{M})$
be arbitrary balls such that
$M:=B(x_{M},r_{M})$
be arbitrary balls such that
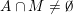 $A\cap M\not =\emptyset$
and
$A\cap M\not =\emptyset$
and
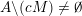 $A\setminus (cM)\not =\emptyset$
for some
$A\setminus (cM)\not =\emptyset$
for some
![]() $c\geqslant 3$
. Then
$c\geqslant 3$
. Then
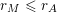 $r_{M}\leqslant r_{A}$
and
$r_{M}\leqslant r_{A}$
and
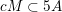 $cM\subset 5A$
.
$cM\subset 5A$
.
A good part of the subsequent argument will follow the same reasoning as given in [Reference Beresnevich and VelaniBV06a, § 5.5]. However, there will also be obvious alterations to the proofs that arise from the different construction of a Cantor set used here. Recall that the measure
![]() $\unicode[STIX]{x1D707}$
is supported on
$\unicode[STIX]{x1D707}$
is supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Without loss of generality, we will make the following two assumptions:
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
. Without loss of generality, we will make the following two assumptions:
(i)
 $D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}\neq \emptyset$
;
$D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}\neq \emptyset$
;(ii) for every
 $n$
large enough
$n$
large enough
 $D$
intersects at least two balls in
$D$
intersects at least two balls in
 $K(n)$
.
$K(n)$
.
If the first of these were false then we would have
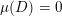 $\unicode[STIX]{x1D707}(D)=0$
as
$\unicode[STIX]{x1D707}(D)=0$
as
![]() $\unicode[STIX]{x1D707}$
is supported on
$\unicode[STIX]{x1D707}$
is supported on
![]() $\mathbb{K}_{\unicode[STIX]{x1D702}}$
and so (24) would trivially follow. If the second assumption were false then
$\mathbb{K}_{\unicode[STIX]{x1D702}}$
and so (24) would trivially follow. If the second assumption were false then
![]() $D$
would have to intersect exactly one ball, say
$D$
would have to intersect exactly one ball, say
![]() $L_{n_{i}}$
, from levels
$L_{n_{i}}$
, from levels
![]() $K_{n_{i}}$
with arbitrarily large
$K_{n_{i}}$
with arbitrarily large
![]() $n_{i}$
. Then, by (36), we would have
$n_{i}$
. Then, by (36), we would have
 $\unicode[STIX]{x1D707}(D)\leqslant \unicode[STIX]{x1D707}(L_{n_{i}})\rightarrow 0$
as
$\unicode[STIX]{x1D707}(D)\leqslant \unicode[STIX]{x1D707}(L_{n_{i}})\rightarrow 0$
as
![]() $i\rightarrow \infty$
and so, again, (24) would be trivially true.
$i\rightarrow \infty$
and so, again, (24) would be trivially true.
By the above two assumptions, we have that there exists a maximum integer
![]() $n$
such that
$n$
such that
 $$\begin{eqnarray}\displaystyle D\text{ intersects at least 2 balls from }K(n) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\text{ intersects at least 2 balls from }K(n) & & \displaystyle\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle D\text{ intersects only one ball }B\text{ from }K(n-1). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\text{ intersects only one ball }B\text{ from }K(n-1). & & \displaystyle \nonumber\end{eqnarray}$$
By our choice of
![]() $r_{0}$
, we have that
$r_{0}$
, we have that
![]() $n>2$
. If
$n>2$
. If
![]() $B$
is the only ball from
$B$
is the only ball from
 $K(n-1)$
which has non-empty intersection with
$K(n-1)$
which has non-empty intersection with
![]() $D$
, we may also assume that
$D$
, we may also assume that
 $r(D)<r(B)$
. To see this, suppose to the contrary that
$r(D)<r(B)$
. To see this, suppose to the contrary that
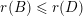 $r(B)\leqslant r(D)$
. Then, since
$r(B)\leqslant r(D)$
. Then, since
 $D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}\subset B$
and
$D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}\subset B$
and
![]() $f$
is increasing, upon recalling (36) we would have
$f$
is increasing, upon recalling (36) we would have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(D)\leqslant \unicode[STIX]{x1D707}(B)\ll \frac{V^{f}(B)}{\unicode[STIX]{x1D702}}=\frac{f(r(B))}{\unicode[STIX]{x1D702}}\leqslant \frac{f(r(D))}{\unicode[STIX]{x1D702}}=\frac{V^{f}(D)}{\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(D)\leqslant \unicode[STIX]{x1D707}(B)\ll \frac{V^{f}(B)}{\unicode[STIX]{x1D702}}=\frac{f(r(B))}{\unicode[STIX]{x1D702}}\leqslant \frac{f(r(D))}{\unicode[STIX]{x1D702}}=\frac{V^{f}(D)}{\unicode[STIX]{x1D702}},\end{eqnarray}$$
and so we would be done.
Now, since
 $K(n,B)$
is a cover for
$K(n,B)$
is a cover for
![]() $D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}$
, we have
$D\cap \mathbb{K}_{\unicode[STIX]{x1D702}}$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(D) & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{L\in K(n,B,i):L\cap D\neq \emptyset }\unicode[STIX]{x1D707}(L)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\unicode[STIX]{x1D707}(L)\nonumber\\ \displaystyle & \stackrel{(36)}{\ll } & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(D) & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{L\in K(n,B,i):L\cap D\neq \emptyset }\unicode[STIX]{x1D707}(L)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\unicode[STIX]{x1D707}(L)\nonumber\\ \displaystyle & \stackrel{(36)}{\ll } & \displaystyle \mathop{\sum }_{i=1}^{l_{B}}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
To estimate the right-hand side of (42) we consider the following types of sub-levels.
Case 1: Sub-levels
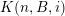 $K(n,B,i)$
for which
$K(n,B,i)$
for which
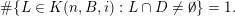 $$\begin{eqnarray}\#\{L\in K(n,B,i):L\cap D\neq \emptyset \}=1.\end{eqnarray}$$
$$\begin{eqnarray}\#\{L\in K(n,B,i):L\cap D\neq \emptyset \}=1.\end{eqnarray}$$
Case 2: Sub-levels
 $K(n,B,i)$
for which
$K(n,B,i)$
for which
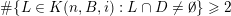 $$\begin{eqnarray}\displaystyle \#\{L\in K(n,B,i):L\cap D\neq \emptyset \}\geqslant 2 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{L\in K(n,B,i):L\cap D\neq \emptyset \}\geqslant 2 & & \displaystyle \nonumber\end{eqnarray}$$
and
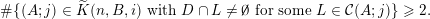 $$\begin{eqnarray}\displaystyle \#\{(A;j)\in \widetilde{K}(n,B,i)\text{ with }D\cap L\neq \emptyset \text{ for some }L\in {\mathcal{C}}(A;j)\}\geqslant 2. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{(A;j)\in \widetilde{K}(n,B,i)\text{ with }D\cap L\neq \emptyset \text{ for some }L\in {\mathcal{C}}(A;j)\}\geqslant 2. & & \displaystyle \nonumber\end{eqnarray}$$
Case 3: Sub-levels
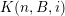 $K(n,B,i)$
for which
$K(n,B,i)$
for which
 $$\begin{eqnarray}\displaystyle \#\{L\in K(n,B,i):L\cap D\neq \emptyset \}\geqslant 2 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{L\in K(n,B,i):L\cap D\neq \emptyset \}\geqslant 2 & & \displaystyle \nonumber\end{eqnarray}$$
and
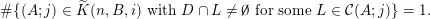 $$\begin{eqnarray}\displaystyle \#\{(A;j)\in \widetilde{K}(n,B,i)\text{ with }D\cap L\neq \emptyset \text{ for some }L\in {\mathcal{C}}(A;j)\}=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{(A;j)\in \widetilde{K}(n,B,i)\text{ with }D\cap L\neq \emptyset \text{ for some }L\in {\mathcal{C}}(A;j)\}=1. & & \displaystyle \nonumber\end{eqnarray}$$
Strictly speaking we also need to consider the sub-levels
 $K(n,B,i)$
for which
$K(n,B,i)$
for which
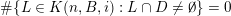 $\#\{L\in K(n,B,i):L\cap D\neq \emptyset \}=0$
. However, these sub-levels do not contribute anything to the sum on the right-hand side of (42).
$\#\{L\in K(n,B,i):L\cap D\neq \emptyset \}=0$
. However, these sub-levels do not contribute anything to the sum on the right-hand side of (42).
Dealing with Case 1. Let
 $K(n,B,i^{\ast })$
denote the first sub-level within Case 1 which has non-empty intersection with
$K(n,B,i^{\ast })$
denote the first sub-level within Case 1 which has non-empty intersection with
![]() $D$
. Then there exists a unique ball
$D$
. Then there exists a unique ball
![]() $L^{\ast }$
in
$L^{\ast }$
in
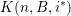 $K(n,B,i^{\ast })$
such that
$K(n,B,i^{\ast })$
such that
 $L^{\ast }\cap D\neq \emptyset$
. By (41) there is another ball
$L^{\ast }\cap D\neq \emptyset$
. By (41) there is another ball
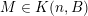 $M\in K(n,B)$
such that
$M\in K(n,B)$
such that
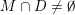 $M\cap D\neq \emptyset$
. By Property (P1),
$M\cap D\neq \emptyset$
. By Property (P1),
![]() $3L^{\ast }$
and
$3L^{\ast }$
and
![]() $3M$
are disjoint. It follows that
$3M$
are disjoint. It follows that
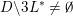 $D\setminus 3L^{\ast }\neq \emptyset$
. Therefore, by Lemma 6, we have that
$D\setminus 3L^{\ast }\neq \emptyset$
. Therefore, by Lemma 6, we have that
 $r(L^{\ast })\leqslant r(D)$
and so, since
$r(L^{\ast })\leqslant r(D)$
and so, since
![]() $f$
is increasing,
$f$
is increasing,
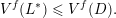 $$\begin{eqnarray}\displaystyle V^{f}(L^{\ast })\leqslant V^{f}(D). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V^{f}(L^{\ast })\leqslant V^{f}(D). & & \displaystyle\end{eqnarray}$$
By Property (P4) we have, for any
 $i\in \{i^{\ast }+1,\ldots ,l_{B}\}$
and any
$i\in \{i^{\ast }+1,\ldots ,l_{B}\}$
and any
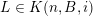 $L\in K(n,B,i)$
, that
$L\in K(n,B,i)$
, that
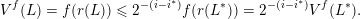 $$\begin{eqnarray}V^{f}(L)=f(r(L))\leqslant 2^{-(i-i^{\ast })}f(r(L^{\ast }))=2^{-(i-i^{\ast })}V^{f}(L^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}V^{f}(L)=f(r(L))\leqslant 2^{-(i-i^{\ast })}f(r(L^{\ast }))=2^{-(i-i^{\ast })}V^{f}(L^{\ast }).\end{eqnarray}$$
Using these inequalities and (43) we see that the contribution to the right-hand side of (42) from Case 1 is:
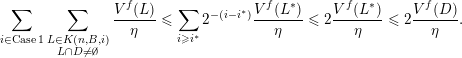 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,1}\mathop{\sum }_{\substack{ L\in K(n,B,i) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\leqslant \mathop{\sum }_{i\geqslant i^{\ast }}2^{-(i-i^{\ast })}\frac{V^{f}(L^{\ast })}{\unicode[STIX]{x1D702}}\leqslant 2\frac{V^{f}(L^{\ast })}{\unicode[STIX]{x1D702}}\leqslant 2\frac{V^{f}(D)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,1}\mathop{\sum }_{\substack{ L\in K(n,B,i) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\leqslant \mathop{\sum }_{i\geqslant i^{\ast }}2^{-(i-i^{\ast })}\frac{V^{f}(L^{\ast })}{\unicode[STIX]{x1D702}}\leqslant 2\frac{V^{f}(L^{\ast })}{\unicode[STIX]{x1D702}}\leqslant 2\frac{V^{f}(D)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
Dealing with Case 2. Let
 $K(n,B,i)$
be any sub-level subject to the conditions of Case 2. Then there exist distinct balls
$K(n,B,i)$
be any sub-level subject to the conditions of Case 2. Then there exist distinct balls
![]() $(A;j)$
and
$(A;j)$
and
![]() $(A^{\prime };j^{\prime })$
in
$(A^{\prime };j^{\prime })$
in
 $\widetilde{K}(n,B,i)$
and balls
$\widetilde{K}(n,B,i)$
and balls
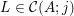 $L\in {\mathcal{C}}(A;j)$
and
$L\in {\mathcal{C}}(A;j)$
and
 $L^{\prime }\in {\mathcal{C}}(A^{\prime };j^{\prime })$
such that
$L^{\prime }\in {\mathcal{C}}(A^{\prime };j^{\prime })$
such that
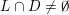 $L\cap D\neq \emptyset$
and
$L\cap D\neq \emptyset$
and
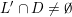 $L^{\prime }\cap D\neq \emptyset$
. Since
$L^{\prime }\cap D\neq \emptyset$
. Since
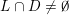 $L\cap D\neq \emptyset$
and
$L\cap D\neq \emptyset$
and
![]() $L\subset A$
we have that
$L\subset A$
we have that
 $A\cap D\neq \emptyset$
. Similarly,
$A\cap D\neq \emptyset$
. Similarly,
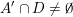 $A^{\prime }\cap D\neq \emptyset$
. Furthermore, by Property (P2), the balls
$A^{\prime }\cap D\neq \emptyset$
. Furthermore, by Property (P2), the balls
![]() $3A$
and
$3A$
and
![]() $3A^{\prime }$
are disjoint and contained in
$3A^{\prime }$
are disjoint and contained in
![]() $B$
. Hence,
$B$
. Hence,
 $D\setminus 3A\neq \emptyset$
. Therefore, by Lemma 6,
$D\setminus 3A\neq \emptyset$
. Therefore, by Lemma 6,
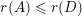 $r(A)\leqslant r(D)$
and
$r(A)\leqslant r(D)$
and
 $A\subset 3A\subset 5D$
. Similarly,
$A\subset 3A\subset 5D$
. Similarly,
 $A^{\prime }\subset 3A^{\prime }\subset 5D$
. Hence, on using (21) we get that the contribution to the right-hand side of (42) from Case 2 is estimated as follows
$A^{\prime }\subset 3A^{\prime }\subset 5D$
. Hence, on using (21) we get that the contribution to the right-hand side of (42) from Case 2 is estimated as follows
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & {\leqslant} & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\#{\mathcal{C}}(A;j)\frac{f(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \stackrel{(21)}{\ll } & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\frac{f(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{l/m}\unicode[STIX]{x1D6F6}_{j}^{-l}\unicode[STIX]{x1D6F6}_{j}^{l}g(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{l/m+1}}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{V^{k}(A)}{\unicode[STIX]{x1D702}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & {\leqslant} & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\#{\mathcal{C}}(A;j)\frac{f(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \stackrel{(21)}{\ll } & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\biggl(\frac{g(\unicode[STIX]{x1D6F6}_{j})^{1/m}}{\unicode[STIX]{x1D6F6}_{j}}\biggr)^{l}\frac{f(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{l/m}\unicode[STIX]{x1D6F6}_{j}^{-l}\unicode[STIX]{x1D6F6}_{j}^{l}g(\unicode[STIX]{x1D6F6}_{j})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{l/m+1}}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{g(\unicode[STIX]{x1D6F6}_{j})^{k/m}}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}\frac{V^{k}(A)}{\unicode[STIX]{x1D702}}.\nonumber\end{eqnarray}$$
Combining this with Properties (P2) and (P5) we get
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & \stackrel{(18)}{\ll } & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}2)}{=} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}A\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}{\mathcal{H}}^{k}(5D)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}5^{k}l_{B}{\mathcal{H}}^{k}(D)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}l_{B}V^{k}(D)\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\leqslant}} & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}\biggl(\frac{2V^{f}(B)}{c_{3}V^{k}(B)}\biggr)V^{k}(D).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & \stackrel{(18)}{\ll } & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}{\mathcal{H}}^{k}(A)\nonumber\\ \displaystyle & \stackrel{(\text{P}2)}{=} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}{\mathcal{H}}^{k}\biggl(\mathop{\bigcup }_{\substack{ (A;j)\in \widetilde{K}(n,B,i) \\ A\subset 5D}}A\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,2}{\mathcal{H}}^{k}(5D)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{c_{1}\unicode[STIX]{x1D702}}5^{k}l_{B}{\mathcal{H}}^{k}(D)\nonumber\\ \displaystyle & \stackrel{(18)}{{\leqslant}} & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}l_{B}V^{k}(D)\nonumber\\ \displaystyle & \stackrel{(\text{P}5)}{{\leqslant}} & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}\biggl(\frac{2V^{f}(B)}{c_{3}V^{k}(B)}\biggr)V^{k}(D).\nonumber\end{eqnarray}$$
Recalling our assumption that
 $r(D)<r(B)$
and the fact that
$r(D)<r(B)$
and the fact that
 $r^{-k}f(r)$
is decreasing, we obtain that
$r^{-k}f(r)$
is decreasing, we obtain that
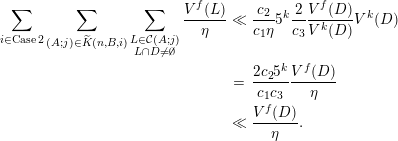 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & \ll & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}\frac{2}{c_{3}}\frac{V^{f}(D)}{V^{k}(D)}V^{k}(D)\nonumber\\ \displaystyle & = & \displaystyle \frac{2c_{2}5^{k}}{c_{1}c_{3}}\frac{V^{f}(D)}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,2}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & \ll & \displaystyle \frac{c_{2}}{c_{1}\unicode[STIX]{x1D702}}5^{k}\frac{2}{c_{3}}\frac{V^{f}(D)}{V^{k}(D)}V^{k}(D)\nonumber\\ \displaystyle & = & \displaystyle \frac{2c_{2}5^{k}}{c_{1}c_{3}}\frac{V^{f}(D)}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Dealing with Case 3. First of all note that for each level
![]() $i$
of Case 3 there exists a unique
$i$
of Case 3 there exists a unique
 $(A_{i};j_{i})\in \widetilde{K}(n,B,i)$
such that
$(A_{i};j_{i})\in \widetilde{K}(n,B,i)$
such that
![]() $D$
has a non-empty intersection with balls in
$D$
has a non-empty intersection with balls in
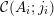 ${\mathcal{C}}(A_{i};j_{i})$
. Let
${\mathcal{C}}(A_{i};j_{i})$
. Let
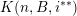 $K(n,B,i^{\ast \ast })$
denote the first sub-level within Case 3. Then there exists a ball
$K(n,B,i^{\ast \ast })$
denote the first sub-level within Case 3. Then there exists a ball
![]() $L^{\ast \ast }$
in
$L^{\ast \ast }$
in
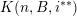 $K(n,B,i^{\ast \ast })$
such that
$K(n,B,i^{\ast \ast })$
such that
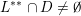 $L^{\ast \ast }\cap D\neq \emptyset$
. By (41) there is another ball
$L^{\ast \ast }\cap D\neq \emptyset$
. By (41) there is another ball
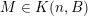 $M\in K(n,B)$
such that
$M\in K(n,B)$
such that
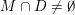 $M\cap D\neq \emptyset$
. By Property (P1),
$M\cap D\neq \emptyset$
. By Property (P1),
![]() $3L^{\ast \ast }$
and
$3L^{\ast \ast }$
and
![]() $3M$
are disjoint. It follows that
$3M$
are disjoint. It follows that
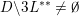 $D\setminus 3L^{\ast \ast }\neq \emptyset$
and therefore, by Lemma 6, we have that
$D\setminus 3L^{\ast \ast }\neq \emptyset$
and therefore, by Lemma 6, we have that
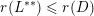 $r(L^{\ast \ast })\leqslant r(D)$
and so, since
$r(L^{\ast \ast })\leqslant r(D)$
and so, since
![]() $g$
is increasing, we have that
$g$
is increasing, we have that
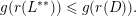 $$\begin{eqnarray}\displaystyle g(r(L^{\ast \ast }))\leqslant g(r(D)). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(r(L^{\ast \ast }))\leqslant g(r(D)). & & \displaystyle\end{eqnarray}$$
Furthermore, by Property (P4), for any
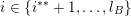 $i\in \{i^{\ast \ast }+1,\ldots ,l_{B}\}$
and any
$i\in \{i^{\ast \ast }+1,\ldots ,l_{B}\}$
and any
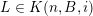 $L\in K(n,B,i)$
we have that
$L\in K(n,B,i)$
we have that
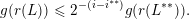 $$\begin{eqnarray}g(r(L))\leqslant 2^{-(i-i^{\ast \ast })}g(r(L^{\ast \ast })).\end{eqnarray}$$
$$\begin{eqnarray}g(r(L))\leqslant 2^{-(i-i^{\ast \ast })}g(r(L^{\ast \ast })).\end{eqnarray}$$
Then, the contribution to the sum (42) from Case 3 is estimated as follows
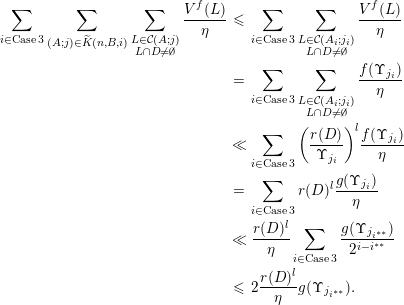 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & {\leqslant} & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A_{i};j_{i}) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A_{i};j_{i}) \\ L\cap D\neq \emptyset }}\frac{f(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\biggl(\frac{r(D)}{\unicode[STIX]{x1D6F6}_{j_{i}}}\biggr)^{l}\frac{f(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}r(D)^{l}\frac{g(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{r(D)^{l}}{\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,3}\frac{g(\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}})}{2^{i-i^{\ast \ast }}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\frac{r(D)^{l}}{\unicode[STIX]{x1D702}}g(\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}} & {\leqslant} & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A_{i};j_{i}) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A_{i};j_{i}) \\ L\cap D\neq \emptyset }}\frac{f(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\biggl(\frac{r(D)}{\unicode[STIX]{x1D6F6}_{j_{i}}}\biggr)^{l}\frac{f(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i\in \text{Case}\,3}r(D)^{l}\frac{g(\unicode[STIX]{x1D6F6}_{j_{i}})}{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{r(D)^{l}}{\unicode[STIX]{x1D702}}\mathop{\sum }_{i\in \text{Case}\,3}\frac{g(\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}})}{2^{i-i^{\ast \ast }}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\frac{r(D)^{l}}{\unicode[STIX]{x1D702}}g(\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}}).\nonumber\end{eqnarray}$$
Noting that
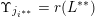 $\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}}=r(L^{\ast \ast })$
and recalling (46) we see that
$\unicode[STIX]{x1D6F6}_{j_{i^{\ast \ast }}}=r(L^{\ast \ast })$
and recalling (46) we see that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\ll 2\frac{r(D)^{l}}{\unicode[STIX]{x1D702}}g(r(D))=2\frac{f(r(D))}{\unicode[STIX]{x1D702}}\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in \text{Case}\,3}\mathop{\sum }_{(A;j)\in \widetilde{K}(n,B,i)}\mathop{\sum }_{\substack{ L\in {\mathcal{C}}(A;j) \\ L\cap D\neq \emptyset }}\frac{V^{f}(L)}{\unicode[STIX]{x1D702}}\ll 2\frac{r(D)^{l}}{\unicode[STIX]{x1D702}}g(r(D))=2\frac{f(r(D))}{\unicode[STIX]{x1D702}}\ll \frac{V^{f}(D)}{\unicode[STIX]{x1D702}}. & & \displaystyle\end{eqnarray}$$
Finally, combining (44), (45) and (47) together with (42) gives
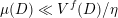 $\unicode[STIX]{x1D707}(D)\ll V^{f}(D)/\unicode[STIX]{x1D702}$
and thus completes the proof of Theorem 1.
$\unicode[STIX]{x1D707}(D)\ll V^{f}(D)/\unicode[STIX]{x1D702}$
and thus completes the proof of Theorem 1.