Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-19T21:30:31.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Martin boundaries of the duals of free unitary quantum groups

Part of: Selfadjoint operator algebras Linear algebraic groups and related topics Markov processes

Published online by Cambridge University Press:  31 May 2019

Sara Malacarne  and
Sergey Neshveyev
Sara Malacarne
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway email [email protected]
Sergey Neshveyev
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a free unitary quantum group 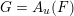$G=A_{u}(F)$, with 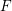$F$ not a unitary 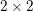$2\times 2$ matrix, we show that the Martin boundary of the dual of 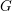$G$ with respect to any 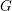$G$-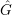${\hat{G}}$-invariant, irreducible, finite-range quantum random walk coincides with the topological boundary defined by Vaes and Vander Vennet. This can be thought of as a quantum analogue of the fact that the Martin boundary of a free group coincides with the space of ends of its Cayley tree.

Keywords

quantum groupMartin boundaryGromov boundaryrandom walks on trees

MSC classification

Primary: 20G42: Quantum groups (quantized function algebras) and their representations 46L65: Quantizations, deformations 60J50: Boundary theory
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 6 , June 2019 , pp. 1171 - 1193
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research leading to these results received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 307663.

References

Ancona, A., Positive harmonic functions and hyperbolicity , in Potential theory – surveys and problems (Prague, 1987), Lecture Notes in Mathematics, vol. 1344 (Springer, Berlin, 1988), 1–23.Google Scholar
Banica, T., Le groupe quantique compact libre U(n) , Comm. Math. Phys. 190 (1997), 143–172.Google Scholar
Biane, Ph., Théorème de Ney-Spitzer sur le dual de SU(2) , Trans. Amer. Math. Soc. 345 (1994), 179–194.Google Scholar
Cartier, P., Fonctions harmoniques sur un arbre , in Symposia Mathematica, Convegno di Calcolo delle Probabilità, INDAM, Rome, 1971 vol. IX (Academic Press, London, 1972), 203–270.Google Scholar
De Rijdt, A. and Vander Vennet, N., Actions of monoidally equivalent compact quantum groups and applications to probabilistic boundaries , Ann. Inst. Fourier (Grenoble) 60 (2010), 169–216.Google Scholar
Derriennic, Y., Marche aléatoire sur le groupe libre et frontière de Martin , Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 32 (1975), 261–276.Google Scholar
Derriennic, Y. and Guivarc’h, Y., Théorème de renouvellement pour les groupes non moyennables , C. R. Acad. Sci. Paris Sér. A-B 277 (1973), A613–A615.Google Scholar
Dynkin, E. B. and Malyutov, M. B., Random walk on groups with a finite number of generators , Dokl. Akad. Nauk SSSR 137 (1961), 1042–1045 (in Russian).Google Scholar
Izumi, M., Non-commutative Poisson boundaries and compact quantum group actions , Adv. Math. 169 (2002), 1–57.Google Scholar
Izumi, M., Neshveyev, S. and Okayasu, R., The ratio set of the harmonic measure of a random walk on a hyperbolic group , Israel J. Math. 163 (2008), 285–316.Google Scholar
Jordans, B. P. A., Convergence to the boundary for random walks on discrete quantum groups and monoidal categories , Münster J. Math. 10 (2017), 287–365.Google Scholar
Kaimanovich, V. A., The Poisson formula for groups with hyperbolic properties , Ann. of Math. (2) 152 (2000), 659–692.Google Scholar
Neshveyev, S. and Tuset, L., The Martin boundary of a discrete quantum group , J. Reine Angew. Math. 568 (2004), 23–70.Google Scholar
Neshveyev, S. and Tuset, L., Compact quantum groups and their representation categories, Cours Spécialisés, vol. 20 (Société Mathématique de France, Paris, 2013).Google Scholar
Neshveyev, S. and Yamashita, M., Categorical duality for Yetter-Drinfeld algebras , Doc. Math. 19 (2014), 1105–1139.Google Scholar
Neshveyev, S. and Yamashita, M., Poisson boundaries of monoidal categories , Ann. Sci. Éc. Norm. Supér. (4) 50 (2017), 927–972.Google Scholar
Picardello, M. A. and Woess, W., Martin boundaries of random walks: ends of trees and groups , Trans. Amer. Math. Soc. 302 (1987), 185–205.Google Scholar
Vaes, S. and Vander Vennet, N., Poisson boundary of the discrete quantum group  u (F) , Compos. Math. 146 (2010), 1073–1095.Google Scholar
Vaes, S. and Vergnioux, R., The boundary of universal discrete quantum groups, exactness, and factoriality , Duke Math. J. 140 (2007), 35–84.Google Scholar
Van Daele, A. and Wang, S., Universal quantum groups , Internat. J. Math. 7 (1996), 255–263.Google Scholar
Vander Vennet, N., Probabilistic boundaries of discrete quantum groups, PhD thesis, Leuven (2008).Google Scholar
Vergnioux, R., Orientation of quantum Cayley trees and applications , J. Reine Angew. Math. 580 (2005), 101–138.Google Scholar
Woess, W., Random walks on infinite graphs and groups, Cambridge Tracts in Mathematics, vol. 138 (Cambridge University Press, Cambridge, 2000).Google Scholar