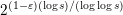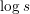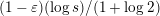Introduction
When
![]() $s\geqslant 2$
is an even integer, the value
$s\geqslant 2$
is an even integer, the value
![]() $\unicode[STIX]{x1D701}(s)$
of the Riemann zeta function is a non-zero rational multiple of
$\unicode[STIX]{x1D701}(s)$
of the Riemann zeta function is a non-zero rational multiple of
![]() $\unicode[STIX]{x1D70B}^{s}$
and, therefore, a transcendental number. On the other hand, no such relation is expected to hold for
$\unicode[STIX]{x1D70B}^{s}$
and, therefore, a transcendental number. On the other hand, no such relation is expected to hold for
![]() $\unicode[STIX]{x1D701}(s)$
when
$\unicode[STIX]{x1D701}(s)$
when
![]() $s\geqslant 3$
is odd; a folklore conjecture states that the numbers
$s\geqslant 3$
is odd; a folklore conjecture states that the numbers
![]() $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
![]() $\unicode[STIX]{x1D701}(3)$
,
$\unicode[STIX]{x1D701}(3)$
,
![]() $\unicode[STIX]{x1D701}(5)$
,
$\unicode[STIX]{x1D701}(5)$
,
![]() $\unicode[STIX]{x1D701}(7),\ldots$
are algebraically independent over the rationals. This conjecture is predicted by Grothendieck’s period conjecture for mixed Tate motives. But both conjectures are far out of reach and we do not even know the transcendence of a single odd zeta value.
$\unicode[STIX]{x1D701}(7),\ldots$
are algebraically independent over the rationals. This conjecture is predicted by Grothendieck’s period conjecture for mixed Tate motives. But both conjectures are far out of reach and we do not even know the transcendence of a single odd zeta value.
It was only in 1978 that Apéry astonished the mathematics community with his proof [Reference ApéryApé79] of the irrationality of
![]() $\unicode[STIX]{x1D701}(3)$
(see [Reference FischlerFis04] for a survey). The next breakthrough was made in 2000 by Ball and Rivoal [Reference Ball and RivoalBR01, Reference RivoalRiv00] who proved the following result.
$\unicode[STIX]{x1D701}(3)$
(see [Reference FischlerFis04] for a survey). The next breakthrough was made in 2000 by Ball and Rivoal [Reference Ball and RivoalBR01, Reference RivoalRiv00] who proved the following result.
Theorem 1 (Ball–Rivoal).
Let
![]() $\unicode[STIX]{x1D700}>0$
. Then for any
$\unicode[STIX]{x1D700}>0$
. Then for any
![]() $s\geqslant 3$
odd and sufficiently large with respect to
$s\geqslant 3$
odd and sufficiently large with respect to
![]() $\unicode[STIX]{x1D700}$
, we have
$\unicode[STIX]{x1D700}$
, we have
Their corresponding result for small
![]() $s$
has been refined several times [Reference ZudilinZud02, Reference Fischler and ZudilinFZ10], but the question whether
$s$
has been refined several times [Reference ZudilinZud02, Reference Fischler and ZudilinFZ10], but the question whether
![]() $\unicode[STIX]{x1D701}(5)$
is irrational remains open. The proof of Theorem 1 involves the well-poised hypergeometric series
$\unicode[STIX]{x1D701}(5)$
is irrational remains open. The proof of Theorem 1 involves the well-poised hypergeometric series
which happens to be a
![]() $\mathbb{Q}$
-linear combination of 1 and odd zeta values when
$\mathbb{Q}$
-linear combination of 1 and odd zeta values when
![]() $s$
is odd and
$s$
is odd and
![]() $n$
is even, and Nesterenko’s linear independence criterion [Reference NesterenkoNes85]. The bound
$n$
is even, and Nesterenko’s linear independence criterion [Reference NesterenkoNes85]. The bound
![]() $(1-\unicode[STIX]{x1D700})(\log s)/(1+\log 2)$
follows from comparison of how small the linear combination is with respect to the size of its coefficients, after multiplying by a common denominator to make them integers. To improve on this bound using the same strategy, one has to find linear combinations that are considerably smaller, with coefficients not too large; it turns out to be a rather difficult task. This may be viewed as an informal explanation of why the lower bound in Theorem 1 has never been improved for large values of
$(1-\unicode[STIX]{x1D700})(\log s)/(1+\log 2)$
follows from comparison of how small the linear combination is with respect to the size of its coefficients, after multiplying by a common denominator to make them integers. To improve on this bound using the same strategy, one has to find linear combinations that are considerably smaller, with coefficients not too large; it turns out to be a rather difficult task. This may be viewed as an informal explanation of why the lower bound in Theorem 1 has never been improved for large values of
![]() $s$
, whereas the theorem itself has been generalized to several other families of numbers.
$s$
, whereas the theorem itself has been generalized to several other families of numbers.
Using (with
![]() $s=20$
) the series
$s=20$
) the series
which is a
![]() $\mathbb{Q}$
-linear combination of 1 and odd zeta values starting from
$\mathbb{Q}$
-linear combination of 1 and odd zeta values starting from
![]() $\unicode[STIX]{x1D701}(5)$
, Rivoal has proved [Reference RivoalRiv02] that among the numbers
$\unicode[STIX]{x1D701}(5)$
, Rivoal has proved [Reference RivoalRiv02] that among the numbers
![]() $\unicode[STIX]{x1D701}(5)$
,
$\unicode[STIX]{x1D701}(5)$
,
![]() $\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(21)$
, at least one is irrational. This result has been improved by the third author [Reference ZudilinZud01]: among the four numbers
$\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(21)$
, at least one is irrational. This result has been improved by the third author [Reference ZudilinZud01]: among the four numbers
![]() $\unicode[STIX]{x1D701}(5)$
,
$\unicode[STIX]{x1D701}(5)$
,
![]() $\unicode[STIX]{x1D701}(7)$
,
$\unicode[STIX]{x1D701}(7)$
,
![]() $\unicode[STIX]{x1D701}(9)$
,
$\unicode[STIX]{x1D701}(9)$
,
![]() $\unicode[STIX]{x1D701}(11)$
, at least one is irrational; and he also showed [Reference ZudilinZud02] that, for any odd
$\unicode[STIX]{x1D701}(11)$
, at least one is irrational; and he also showed [Reference ZudilinZud02] that, for any odd
![]() $\ell \geqslant 1$
, there is an irrational number among
$\ell \geqslant 1$
, there is an irrational number among
![]() $\unicode[STIX]{x1D701}(\ell \,+\,2),\unicode[STIX]{x1D701}(\ell \,+\,4),\ldots ,\unicode[STIX]{x1D701}(8\ell \,-\,1)$
. Proofs of these results do not require use of linear independence criteria: if a sequence of
$\unicode[STIX]{x1D701}(\ell \,+\,2),\unicode[STIX]{x1D701}(\ell \,+\,4),\ldots ,\unicode[STIX]{x1D701}(8\ell \,-\,1)$
. Proofs of these results do not require use of linear independence criteria: if a sequence of
![]() $\mathbb{Z}$
-linear combinations of real numbers from a given (fixed) collection tends to 0, and is non-zero infinitely often, then at least one of these numbers is irrational. A drawback of this approach is that it only allows one to prove that one number in a family is irrational.
$\mathbb{Z}$
-linear combinations of real numbers from a given (fixed) collection tends to 0, and is non-zero infinitely often, then at least one of these numbers is irrational. A drawback of this approach is that it only allows one to prove that one number in a family is irrational.
The situation drastically changed when the third author introduced [Reference ZudilinZud18] a new method (see also [Reference Krattenthaler and ZudilinKZ19]). He casts (with
![]() $s=25$
) the rational function in the form
$s=25$
) the rational function in the form
and proves that both series
are
![]() $\mathbb{Q}$
-linear combinations of
$\mathbb{Q}$
-linear combinations of
![]() $1,\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
with related coefficients. This allows him to eliminate one odd zeta value, and to prove that at least two zeta values among
$1,\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
with related coefficients. This allows him to eliminate one odd zeta value, and to prove that at least two zeta values among
![]() $\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(25)$
are irrational. In view of Apéry’s theorem, the result means that one number among
$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(25)$
are irrational. In view of Apéry’s theorem, the result means that one number among
![]() $\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(25)$
is irrational, nothing really novel, but the method of proof is new and more elementary than those in [Reference RivoalRiv02, Reference ZudilinZud01] as it avoids use of the saddle-point method. More importantly, the method allows one to prove the irrationality of at least two zeta values in a family without having to produce very small linear forms. The same strategy has been adopted by Rivoal and the third author [Reference Rivoal and ZudilinRZ18] to prove that among
$\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(25)$
is irrational, nothing really novel, but the method of proof is new and more elementary than those in [Reference RivoalRiv02, Reference ZudilinZud01] as it avoids use of the saddle-point method. More importantly, the method allows one to prove the irrationality of at least two zeta values in a family without having to produce very small linear forms. The same strategy has been adopted by Rivoal and the third author [Reference Rivoal and ZudilinRZ18] to prove that among
![]() $\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(69)$
, at least two numbers are irrational.
$\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(69)$
, at least two numbers are irrational.
The method in [Reference ZudilinZud18] has been generalized by the second author [Reference SprangSpr18], who introduces another integer parameter
![]() $D>1$
and considers the rational function
$D>1$
and considers the rational function
He proves that for any divisor
![]() $d$
of
$d$
of
![]() $D$
the series
$D$
the series
is a
![]() $\mathbb{Q}$
-linear combination of
$\mathbb{Q}$
-linear combination of
![]() $1,\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
. The crucial point of this construction is that each
$1,\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
. The crucial point of this construction is that each
![]() $\unicode[STIX]{x1D701}(i)$
appears in this
$\unicode[STIX]{x1D701}(i)$
appears in this
![]() $\mathbb{Q}$
-linear combination with a coefficient that depends on
$\mathbb{Q}$
-linear combination with a coefficient that depends on
![]() $d$
in a very simple way. This makes it possible to eliminate from the entire collection of these linear combinations as many odd zeta values as the number of divisors of
$d$
in a very simple way. This makes it possible to eliminate from the entire collection of these linear combinations as many odd zeta values as the number of divisors of
![]() $D$
. Finally, taking
$D$
. Finally, taking
![]() $D$
equal to a power of 2 and
$D$
equal to a power of 2 and
![]() $s$
sufficiently large with respect to
$s$
sufficiently large with respect to
![]() $D$
, the second author proves that at least
$D$
, the second author proves that at least
![]() $\log D/\text{log}\,2$
numbers are irrational among
$\log D/\text{log}\,2$
numbers are irrational among
![]() $\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
. This strategy represents a new proof that
$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(s)$
. This strategy represents a new proof that
![]() $\unicode[STIX]{x1D701}(i)$
is irrational for infinitely many odd integers
$\unicode[STIX]{x1D701}(i)$
is irrational for infinitely many odd integers
![]() $i$
.
$i$
.
Building upon the approach in [Reference ZudilinZud18, Reference SprangSpr18], we prove the following result (announced in [Reference Fischler, Sprang and ZudilinFSZ18]).
Theorem 2. Let
![]() $\unicode[STIX]{x1D700}>0$
, and let
$\unicode[STIX]{x1D700}>0$
, and let
![]() $s\geqslant 3$
be an odd integer sufficiently large with respect to
$s\geqslant 3$
be an odd integer sufficiently large with respect to
![]() $\unicode[STIX]{x1D700}$
. Then among the numbers
$\unicode[STIX]{x1D700}$
. Then among the numbers
at least
are irrational.
In this result, the lower bound is asymptotically greater than
![]() $\exp (\sqrt{\log s})$
, and than any power of
$\exp (\sqrt{\log s})$
, and than any power of
![]() $\log s$
; ‘to put it roughly, [it is] much more like a power of
$\log s$
; ‘to put it roughly, [it is] much more like a power of
![]() $s$
than a power of
$s$
than a power of
![]() $\log s$
’ [Reference Hardy and WrightHW79, ch. XVIII, § 1].
$\log s$
’ [Reference Hardy and WrightHW79, ch. XVIII, § 1].
In comparison, Theorem 1 gives only
![]() $(1-\unicode[STIX]{x1D700})(\log s)/(1+\log 2)$
irrational odd zeta values, but they are linearly independent over the rationals, whereas Theorem 2 ends up only with their irrationality.
$(1-\unicode[STIX]{x1D700})(\log s)/(1+\log 2)$
irrational odd zeta values, but they are linearly independent over the rationals, whereas Theorem 2 ends up only with their irrationality.
Our proof of Theorem 2 follows the above-mentioned strategy of the second and third authors. The main new ingredient, compared to the proof in [Reference SprangSpr18], is to take
![]() $D$
large (about
$D$
large (about
![]() $s^{1-2\unicode[STIX]{x1D700}}$
) and equal to the product of the first prime numbers (the so-called primorial); such a number has asymptotically the largest possible number of divisors with respect to its size (see [Reference Hardy and WrightHW79, ch. XVIII, § 1]). To perform the required elimination of a prescribed set of odd zeta values, we need to establish that a certain auxiliary matrix is invertible. Whereas the second author’s choice of
$s^{1-2\unicode[STIX]{x1D700}}$
) and equal to the product of the first prime numbers (the so-called primorial); such a number has asymptotically the largest possible number of divisors with respect to its size (see [Reference Hardy and WrightHW79, ch. XVIII, § 1]). To perform the required elimination of a prescribed set of odd zeta values, we need to establish that a certain auxiliary matrix is invertible. Whereas the second author’s choice of
![]() $D$
in [Reference SprangSpr18] allows him to deal with elementary properties of a Vandermonde matrix, we use at this step a generalization of the corresponding result. We give three different proofs of the latter, based on arguments from combinatorics of partitions, from linear algebra accompanied with a lemma of Fekete, and from analysis using Rolle’s theorem.
$D$
in [Reference SprangSpr18] allows him to deal with elementary properties of a Vandermonde matrix, we use at this step a generalization of the corresponding result. We give three different proofs of the latter, based on arguments from combinatorics of partitions, from linear algebra accompanied with a lemma of Fekete, and from analysis using Rolle’s theorem.
The structure of this paper is as follows. In § 1 we construct linear forms in values of the Hurwitz zeta function. Denominators of the coefficients are studied in § 2; and the asymptotics of the linear forms are dealt with in § 3. Section 4 is devoted to the proof that an auxiliary matrix is invertible. Finally, we establish Theorem 2 in § 5.
1 Construction of linear forms
From now on we let
![]() $s$
,
$s$
,
![]() $D$
be positive integers such that
$D$
be positive integers such that
![]() $s\geqslant 3D$
; we assume that
$s\geqslant 3D$
; we assume that
![]() $s$
is odd. Let
$s$
is odd. Let
![]() $n$
be a positive integer, such that
$n$
be a positive integer, such that
![]() $Dn$
is even. Consider the rational function
$Dn$
is even. Consider the rational function
which, of course, depends also on
![]() $s$
and
$s$
and
![]() $D$
. Notice that the difference between
$D$
. Notice that the difference between
![]() $R_{n}(t)$
and the corresponding function in [Reference SprangSpr18] is in the factor
$R_{n}(t)$
and the corresponding function in [Reference SprangSpr18] is in the factor
![]() $D^{3Dn}$
instead of
$D^{3Dn}$
instead of
![]() $D^{6(D-1)n}$
(see Equation (0.2)).
$D^{6(D-1)n}$
(see Equation (0.2)).
Similar rational functions have already been considered; see [Reference Rivoal and ZudilinRZ03] for the case
![]() $D=2$
and [Reference NashNas04, Reference NishimotoNis11, Reference FischlerFis18] for general
$D=2$
and [Reference NashNas04, Reference NishimotoNis11, Reference FischlerFis18] for general
![]() $D$
. However, the ‘central’ factors
$D$
. However, the ‘central’ factors
![]() $t\,-\,n\,+\,j/D$
with
$t\,-\,n\,+\,j/D$
with
![]() $Dn<j<2Dn$
are missing, and (as the second author noticed [Reference SprangSpr18]) they play a central role in the arithmetic estimates (see Lemma 2 below).
$Dn<j<2Dn$
are missing, and (as the second author noticed [Reference SprangSpr18]) they play a central role in the arithmetic estimates (see Lemma 2 below).
Remark 1. Though one can implement an additional parameter
![]() $r$
in the definition of the rational function
$r$
in the definition of the rational function
![]() $R_{n}(t)$
, in a way similar to that for the Ball–Rivoal series (0.1), we have verified that this does not bring any improvement to the result of Theorem 2.
$R_{n}(t)$
, in a way similar to that for the Ball–Rivoal series (0.1), we have verified that this does not bring any improvement to the result of Theorem 2.
The rational function
![]() $R_{n}(t)$
has a partial fraction expansion
$R_{n}(t)$
has a partial fraction expansion
For any
![]() $j\in \{1,\ldots ,D\}$
, take
$j\in \{1,\ldots ,D\}$
, take
This series converges because of the following estimate for the degree of the rational function:
We recall that the Lerch zeta function is defined by the convergent series
for
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{R}_{{>}0}$
,
$\unicode[STIX]{x1D6FC}\in \mathbb{R}_{{>}0}$
,
![]() $z\in \mathbb{C}$
and
$z\in \mathbb{C}$
and
![]() $i\in \mathbb{Z}$
with either
$i\in \mathbb{Z}$
with either
![]() $|z|<1$
, or
$|z|<1$
, or
![]() $|z|=1$
and
$|z|=1$
and
![]() $i\geqslant 2$
; the Hurwitz zeta function is its special case
$i\geqslant 2$
; the Hurwitz zeta function is its special case
The following lemma is precisely [Reference SprangSpr18, Lemma 1.5]; the change of the normalizing factor
![]() $D^{3Dn}$
does not affect the statement.
$D^{3Dn}$
does not affect the statement.
Lemma 1. For each
![]() $j\in \{1,\ldots ,D\}$
, we have
$j\in \{1,\ldots ,D\}$
, we have
 $$\begin{eqnarray}r_{n,j}=\unicode[STIX]{x1D70C}_{0,j}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}\unicode[STIX]{x1D701}\biggl(i,\frac{j}{D}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}r_{n,j}=\unicode[STIX]{x1D70C}_{0,j}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}\unicode[STIX]{x1D701}\biggl(i,\frac{j}{D}\biggr),\end{eqnarray}$$
where
does not depend on
![]() $j$
, and
$j$
, and
Proof. We follow the strategy of proofs in [Reference ZudilinZud18, Lemma 3] and [Reference SprangSpr18, Lemma 1.5]. Let
![]() $z$
be a real number such that
$z$
be a real number such that
![]() $0<z<1$
. We have
$0<z<1$
. We have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=1}^{\infty }R_{n}\biggl(m+\frac{j}{D}\biggr)z^{m} & = & \displaystyle \mathop{\sum }_{m=1}^{\infty }\mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}\frac{a_{i,k}z^{m}}{(m+k+j/D)^{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}a_{i,k}z^{-k}\mathop{\sum }_{m=1}^{\infty }\frac{z^{m+k}}{(m+k+j/D)^{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}a_{i,k}z^{-k}\biggl(\unicode[STIX]{x1D6F7}\biggl(z,i,\frac{j}{D}\biggr)-\mathop{\sum }_{\ell =0}^{k}\frac{z^{\ell }}{(\ell +j/D)^{i}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=1}^{\infty }R_{n}\biggl(m+\frac{j}{D}\biggr)z^{m} & = & \displaystyle \mathop{\sum }_{m=1}^{\infty }\mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}\frac{a_{i,k}z^{m}}{(m+k+j/D)^{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}a_{i,k}z^{-k}\mathop{\sum }_{m=1}^{\infty }\frac{z^{m+k}}{(m+k+j/D)^{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{k=0}^{n}a_{i,k}z^{-k}\biggl(\unicode[STIX]{x1D6F7}\biggl(z,i,\frac{j}{D}\biggr)-\mathop{\sum }_{\ell =0}^{k}\frac{z^{\ell }}{(\ell +j/D)^{i}}\biggr).\nonumber\end{eqnarray}$$
Now we let
![]() $z$
tend to 1 in the equality we have obtained; the left-hand side tends to
$z$
tend to 1 in the equality we have obtained; the left-hand side tends to
![]() $r_{n,j}$
. On the right-hand side, the term involving the Lerch function with
$r_{n,j}$
. On the right-hand side, the term involving the Lerch function with
![]() $i=1$
has coefficient
$i=1$
has coefficient
![]() $\sum _{k=0}^{n}a_{1,k}z^{-k}$
. Since
$\sum _{k=0}^{n}a_{1,k}z^{-k}$
. Since
![]() $\unicode[STIX]{x1D6F7}(z,1,j/D)$
has only a logarithmic divergence as
$\unicode[STIX]{x1D6F7}(z,1,j/D)$
has only a logarithmic divergence as
![]() $z\rightarrow 1$
and
$z\rightarrow 1$
and
this term tends to 0 as
![]() $z\rightarrow 1$
. All other terms have finite limits as
$z\rightarrow 1$
. All other terms have finite limits as
![]() $z\rightarrow 1$
, so that
$z\rightarrow 1$
, so that
where
![]() $\unicode[STIX]{x1D70C}_{0,j}$
is given by Equation (1.2), and
$\unicode[STIX]{x1D70C}_{0,j}$
is given by Equation (1.2), and
![]() $\unicode[STIX]{x1D70C}_{i}=\sum _{k=0}^{n}a_{i,k}$
for any
$\unicode[STIX]{x1D70C}_{i}=\sum _{k=0}^{n}a_{i,k}$
for any
![]() $i\in \{2,\ldots ,s\}$
.
$i\in \{2,\ldots ,s\}$
.
To complete the proof, we apply the symmetry phenomenon of [Reference Ball and RivoalBR01, Reference RivoalRiv00]. Since
![]() $s$
is odd and
$s$
is odd and
![]() $Dn$
is even we have
$Dn$
is even we have
![]() $R_{n}(-n-t)=-\!R_{n}(t)$
. Now the partial fraction expansion (1.1) is unique, so that
$R_{n}(-n-t)=-\!R_{n}(t)$
. Now the partial fraction expansion (1.1) is unique, so that
![]() $a_{i,n-k}=(-1)^{i+1}a_{i,k}$
for any
$a_{i,n-k}=(-1)^{i+1}a_{i,k}$
for any
![]() $i$
and
$i$
and
![]() $k$
. This implies that
$k$
. This implies that
![]() $\unicode[STIX]{x1D70C}_{i}=0$
when
$\unicode[STIX]{x1D70C}_{i}=0$
when
![]() $i$
is even, and Lemma 1 follows.◻
$i$
is even, and Lemma 1 follows.◻
2 Arithmetic estimates
As usual, we let
![]() $d_{n}=\operatorname{lcm}(1,2,\ldots ,n)$
.
$d_{n}=\operatorname{lcm}(1,2,\ldots ,n)$
.
Lemma 2. We have
and
For part (2.1) we use the strategy of the proof of [Reference FischlerFis18, Lemma 4.5]; note that [Reference SprangSpr18, Lemma 1.3] does not apply in our present situation because of the different normalization of the rational function
![]() $R_{n}(t)$
compared to that in (0.2). To establish (2.2) we follow the proof of [Reference SprangSpr18, Lemma 1.4]; we use
$R_{n}(t)$
compared to that in (0.2). To establish (2.2) we follow the proof of [Reference SprangSpr18, Lemma 1.4]; we use
![]() $d_{n+1}$
here instead of
$d_{n+1}$
here instead of
![]() $d_{n}$
to include the case corresponding to
$d_{n}$
to include the case corresponding to
![]() $j=D$
.
$j=D$
.
Proof of Lemma 2.
For any
![]() $\unicode[STIX]{x1D6FC}\in (1/D)\mathbb{Z}$
we introduce
$\unicode[STIX]{x1D6FC}\in (1/D)\mathbb{Z}$
we introduce
where
![]() $A_{\unicode[STIX]{x1D6FC},k}$
is an integer in view of the explicit formulas
$A_{\unicode[STIX]{x1D6FC},k}$
is an integer in view of the explicit formulas
 $$\begin{eqnarray}(-1)^{k}A_{\unicode[STIX]{x1D6FC},k}=\binom{n}{k}\frac{\mathop{\prod }_{j=1}^{n}(D(\unicode[STIX]{x1D6FC}-k)+j)}{n!}=\left\{\begin{array}{@{}ll@{}}\displaystyle \binom{n}{k}\binom{D(\unicode[STIX]{x1D6FC}-k)+n}{n}\quad & \displaystyle \text{if}\;\unicode[STIX]{x1D6FC}-k\geqslant 0,\\ \displaystyle 0\quad & \displaystyle \text{if}\;\frac{-n}{D}\leqslant \unicode[STIX]{x1D6FC}-k<0,\\ \displaystyle (-1)^{n}\binom{n}{k}\binom{D(k-\unicode[STIX]{x1D6FC})-1}{n}\quad & \displaystyle \text{if}\;\unicode[STIX]{x1D6FC}-k<\frac{-n}{D}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(-1)^{k}A_{\unicode[STIX]{x1D6FC},k}=\binom{n}{k}\frac{\mathop{\prod }_{j=1}^{n}(D(\unicode[STIX]{x1D6FC}-k)+j)}{n!}=\left\{\begin{array}{@{}ll@{}}\displaystyle \binom{n}{k}\binom{D(\unicode[STIX]{x1D6FC}-k)+n}{n}\quad & \displaystyle \text{if}\;\unicode[STIX]{x1D6FC}-k\geqslant 0,\\ \displaystyle 0\quad & \displaystyle \text{if}\;\frac{-n}{D}\leqslant \unicode[STIX]{x1D6FC}-k<0,\\ \displaystyle (-1)^{n}\binom{n}{k}\binom{D(k-\unicode[STIX]{x1D6FC})-1}{n}\quad & \displaystyle \text{if}\;\unicode[STIX]{x1D6FC}-k<\frac{-n}{D}.\end{array}\right.\end{eqnarray}$$
We also consider
so that
From this expression we compute the partial fraction expansion of
![]() $R_{n}(t)$
using the rules
$R_{n}(t)$
using the rules
A denominator appears each time the second rule is applied, and the denominator is always a divisor of
![]() $d_{n}$
(see [Reference ColmezCol03] or [Reference ZudilinZud18, Lemma 1]). This happens
$d_{n}$
(see [Reference ColmezCol03] or [Reference ZudilinZud18, Lemma 1]). This happens
![]() $s\,+\,1\,-\,i$
times in each term that contributes to
$s\,+\,1\,-\,i$
times in each term that contributes to
![]() $a_{i,k}$
because there are
$a_{i,k}$
because there are
![]() $s\,+\,1$
factors in the product (2.3) (apart from
$s\,+\,1$
factors in the product (2.3) (apart from
![]() $t\,-\,n$
). Therefore,
$t\,-\,n$
). Therefore,
implying (2.1).
We now proceed with the second part of Lemma 2, that is, with demonstrating the inclusions (2.2). Recall from Lemma 1 that
If
![]() $j=D$
then
$j=D$
then
are integers for any
![]() $k$
,
$k$
,
![]() $\ell$
and
$\ell$
and
![]() $i$
, so that
$i$
, so that
![]() $d_{n+1}^{s+1}\unicode[STIX]{x1D70C}_{0,j}\in \mathbb{Z}$
. From now on, we assume that
$d_{n+1}^{s+1}\unicode[STIX]{x1D70C}_{0,j}\in \mathbb{Z}$
. From now on, we assume that
![]() $1\leqslant j\leqslant D\,-\,1$
and we prove that for any
$1\leqslant j\leqslant D\,-\,1$
and we prove that for any
![]() $k$
and any
$k$
and any
![]() $\ell$
the internal sum over
$\ell$
the internal sum over
![]() $i$
in Equation (2.4) is an integer. With this aim in mind, fix integers
$i$
in Equation (2.4) is an integer. With this aim in mind, fix integers
![]() $k_{0}$
and
$k_{0}$
and
![]() $\ell _{0}$
, with
$\ell _{0}$
, with
![]() $0\leqslant \ell _{0}\leqslant k_{0}\leqslant n$
, and assume that the corresponding sum is not an integer. Recall that
$0\leqslant \ell _{0}\leqslant k_{0}\leqslant n$
, and assume that the corresponding sum is not an integer. Recall that
![]() $R_{n}$
was defined at the beginning of § 1, and vanishes at all non-integer values of
$R_{n}$
was defined at the beginning of § 1, and vanishes at all non-integer values of
![]() $n\,-\,j^{\prime }/D$
with
$n\,-\,j^{\prime }/D$
with
![]() $0\leqslant j^{\prime }\leqslant 3Dn$
. Since
$0\leqslant j^{\prime }\leqslant 3Dn$
. Since
![]() $1\leqslant j\leqslant D\,-\,1$
we have
$1\leqslant j\leqslant D\,-\,1$
we have
![]() $R_{n}(\ell _{0}\,-\,k_{0}\,+\,j/D)=0$
; it follows from (1.1) that
$R_{n}(\ell _{0}\,-\,k_{0}\,+\,j/D)=0$
; it follows from (1.1) that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}\frac{d_{n+1}^{s+1}a_{i,k_{0}}}{(\ell _{0}+j/D)^{i}}=-\mathop{\sum }_{\substack{ k=0 \\ k\neq k_{0}}}^{n}\mathop{\sum }_{i=1}^{s}\frac{d_{n+1}^{s+1}a_{i,k}}{(\ell _{0}-k_{0}+k+j/D)^{i}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}\frac{d_{n+1}^{s+1}a_{i,k_{0}}}{(\ell _{0}+j/D)^{i}}=-\mathop{\sum }_{\substack{ k=0 \\ k\neq k_{0}}}^{n}\mathop{\sum }_{i=1}^{s}\frac{d_{n+1}^{s+1}a_{i,k}}{(\ell _{0}-k_{0}+k+j/D)^{i}}.\end{eqnarray}$$
By our assumption this rational number is not an integer: it has negative
![]() $p$
-adic valuation for at least one prime number
$p$
-adic valuation for at least one prime number
![]() $p$
. Therefore, on either side of (2.5) there is at least one term with negative
$p$
. Therefore, on either side of (2.5) there is at least one term with negative
![]() $p$
-adic valuation: there exist
$p$
-adic valuation: there exist
![]() $i_{0},i_{1}\in \{1,\ldots ,s\}$
and
$i_{0},i_{1}\in \{1,\ldots ,s\}$
and
![]() $k_{1}\in \{0,\ldots ,n\}$
,
$k_{1}\in \{0,\ldots ,n\}$
,
![]() $k_{1}\neq k_{0}$
, such that
$k_{1}\neq k_{0}$
, such that
Since
![]() $d_{n+1}^{s+1-i}a_{i,k}\in \mathbb{Z}$
for any
$d_{n+1}^{s+1-i}a_{i,k}\in \mathbb{Z}$
for any
![]() $i$
and
$i$
and
![]() $k$
, this leads to
$k$
, this leads to
implying
As
![]() $k_{0}\,-\,k_{1}=(\ell _{0}\,+\,j/D)\,-\,(\ell _{0}\,-\,k_{0}\,+\,k_{1}\,+\,j/D)$
, we deduce that
$k_{0}\,-\,k_{1}=(\ell _{0}\,+\,j/D)\,-\,(\ell _{0}\,-\,k_{0}\,+\,k_{1}\,+\,j/D)$
, we deduce that
![]() $v_{p}(k_{0}\,-\,k_{1})>v_{p}(d_{n+1})$
, which is impossible in view of the inequalities
$v_{p}(k_{0}\,-\,k_{1})>v_{p}(d_{n+1})$
, which is impossible in view of the inequalities
![]() $0<|k_{0}\,-\,k_{1}|\leqslant n$
. The contradiction completes the proof of Lemma 2.◻
$0<|k_{0}\,-\,k_{1}|\leqslant n$
. The contradiction completes the proof of Lemma 2.◻
Remark 2. It is made explicit in [Reference Rivoal and ZudilinRZ18] (though for a particular situation considered there), that the inclusions in Lemma 2 can be sharpened into the form
and
where
![]() $\unicode[STIX]{x1D6F7}_{n}=\unicode[STIX]{x1D6F7}_{n}(D)$
is a certain product over primes in the range
$\unicode[STIX]{x1D6F7}_{n}=\unicode[STIX]{x1D6F7}_{n}(D)$
is a certain product over primes in the range
![]() $2\leqslant p\leqslant n$
, whose asymptotic behaviour
$2\leqslant p\leqslant n$
, whose asymptotic behaviour
can be controlled by means of the prime number theorem. It is possible to show that the quantity
![]() $\unicode[STIX]{x1D719}(D)/D$
increases to
$\unicode[STIX]{x1D719}(D)/D$
increases to
![]() $\infty$
and at the same time
$\infty$
and at the same time
![]() $\unicode[STIX]{x1D719}(D)/(D\log ^{\unicode[STIX]{x1D700}}D)\rightarrow 0$
as
$\unicode[STIX]{x1D719}(D)/(D\log ^{\unicode[STIX]{x1D700}}D)\rightarrow 0$
as
![]() $D\rightarrow \infty$
, for any choice of
$D\rightarrow \infty$
, for any choice of
![]() $\unicode[STIX]{x1D700}>0$
. Later, we choose
$\unicode[STIX]{x1D700}>0$
. Later, we choose
![]() $D$
such that
$D$
such that
![]() $D\log D<s$
, implying that the arithmetic gain coming from the factors
$D\log D<s$
, implying that the arithmetic gain coming from the factors
![]() $\unicode[STIX]{x1D6F7}_{n}^{-1}$
is asymptotically negligible as
$\unicode[STIX]{x1D6F7}_{n}^{-1}$
is asymptotically negligible as
![]() $s\rightarrow \infty$
. For the same reason, any arithmetic improvement like the one established in [Reference Krattenthaler and RivoalKR07] would have no influence on the statement of Theorem 2.
$s\rightarrow \infty$
. For the same reason, any arithmetic improvement like the one established in [Reference Krattenthaler and RivoalKR07] would have no influence on the statement of Theorem 2.
3 Asymptotic estimates of the linear forms
The following lemma is proved along the same lines as [Reference SprangSpr18, Lemma 2.1] (see also [Reference ZudilinZud18, Lemma 4] and the second proof of [Reference Ball and RivoalBR01, Lemme 3]). The difference is that here we only assume
![]() $s/(D\log D)$
to be sufficiently large, whereas in [Reference SprangSpr18] parameter
$s/(D\log D)$
to be sufficiently large, whereas in [Reference SprangSpr18] parameter
![]() $D$
is fixed and
$D$
is fixed and
![]() $s\rightarrow \infty$
.
$s\rightarrow \infty$
.
Lemma 3. Assume that
![]() $D\geqslant 2$
and
$D\geqslant 2$
and
Then
where
and
![]() $x_{0}$
is the unique positive root of the polynomial
$x_{0}$
is the unique positive root of the polynomial
Proof. For
![]() $j\in \{1,\ldots ,D\}$
and
$j\in \{1,\ldots ,D\}$
and
![]() $k\geqslant 0$
, let
$k\geqslant 0$
, let
so that
is a sum of positive terms. We have
implying that, for any
![]() $j$
, the quotient
$j$
, the quotient
![]() $c_{k+1,j}/c_{k,j}$
tends to
$c_{k+1,j}/c_{k,j}$
tends to
![]() $f(\unicode[STIX]{x1D705})$
as
$f(\unicode[STIX]{x1D705})$
as
![]() $n\rightarrow \infty$
assuming
$n\rightarrow \infty$
assuming
![]() $k\sim \unicode[STIX]{x1D705}n$
for
$k\sim \unicode[STIX]{x1D705}n$
for
![]() $\unicode[STIX]{x1D705}>0$
fixed, where
$\unicode[STIX]{x1D705}>0$
fixed, where
For the logarithmic derivative of this function we have
with
![]() $a=s\,+\,1\,-\,3D>0$
and
$a=s\,+\,1\,-\,3D>0$
and
![]() $c=-6D<0$
, hence the derivative
$c=-6D<0$
, hence the derivative
![]() $f^{\prime }(x)$
vanishes at exactly one positive real number
$f^{\prime }(x)$
vanishes at exactly one positive real number
![]() $x_{1}$
. This means that the function
$x_{1}$
. This means that the function
![]() $f(x)$
decreases on
$f(x)$
decreases on
![]() $(0,x_{1}]$
and increases on
$(0,x_{1}]$
and increases on
![]() $[x_{1},+\infty )$
. Since
$[x_{1},+\infty )$
. Since
![]() $\lim _{x\rightarrow 0^{+}}f(x)=+\infty$
and
$\lim _{x\rightarrow 0^{+}}f(x)=+\infty$
and
![]() $\lim _{x\rightarrow +\infty }f(x)=1$
, we deduce that there exists a unique positive real number
$\lim _{x\rightarrow +\infty }f(x)=1$
, we deduce that there exists a unique positive real number
![]() $x_{0}$
such that
$x_{0}$
such that
![]() $f(x_{0})=1$
.
$f(x_{0})=1$
.
Let us now prove (3.2). As in [Reference de BruijndBru81, § 3.4] we wish to demonstrate that the asymptotic behaviour of
![]() $r_{n,j}$
is governed by the terms
$r_{n,j}$
is governed by the terms
![]() $c_{k,j}$
with
$c_{k,j}$
with
![]() $k$
close to
$k$
close to
![]() $x_{0}n$
(see Equation (3.8) below). To begin with, notice that
$x_{0}n$
(see Equation (3.8) below). To begin with, notice that
 $$\begin{eqnarray}\displaystyle c_{k,j} & = & \displaystyle D^{-1}n!^{s+1-3D}\frac{\mathop{\prod }_{\ell =0}^{3Dn}(Dk+j+\ell )}{\mathop{\prod }_{\ell =0}^{n}(n+k+\ell +j/D)^{s+1}}\nonumber\\ \displaystyle & = & \displaystyle D^{-1}n!^{s+1-3D}\frac{(3Dn+Dk+j)!}{(Dk+j-1)!}\frac{\unicode[STIX]{x1D6E4}(n+k+j/D)^{s+1}}{\unicode[STIX]{x1D6E4}(2n+k+1+j/D)^{s+1}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,j} & = & \displaystyle D^{-1}n!^{s+1-3D}\frac{\mathop{\prod }_{\ell =0}^{3Dn}(Dk+j+\ell )}{\mathop{\prod }_{\ell =0}^{n}(n+k+\ell +j/D)^{s+1}}\nonumber\\ \displaystyle & = & \displaystyle D^{-1}n!^{s+1-3D}\frac{(3Dn+Dk+j)!}{(Dk+j-1)!}\frac{\unicode[STIX]{x1D6E4}(n+k+j/D)^{s+1}}{\unicode[STIX]{x1D6E4}(2n+k+1+j/D)^{s+1}}.\nonumber\end{eqnarray}$$
Denoting by
![]() $k_{0}(n)$
the integer part of
$k_{0}(n)$
the integer part of
![]() $x_{0}n$
and applying the Stirling formula to the factorial and gamma factors we obtain, as
$x_{0}n$
and applying the Stirling formula to the factorial and gamma factors we obtain, as
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
 $$\begin{eqnarray}\displaystyle c_{k_{0}(n),j}^{1/n} & {\sim} & \displaystyle \biggl(\frac{n}{e}\biggr)^{s+1-3D}\biggl(\frac{3Dn+Dk_{0}(n)+j}{e}\biggr)^{3D+Dx_{0}}\biggl(\frac{e}{Dk_{0}(n)+j-1}\biggr)^{Dx_{0}}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{n+k_{0}(n)+j/D}{e}\biggr)^{(s+1)(x_{0}+1)}\biggl(\frac{e}{2n+k_{0}(n)+j/D+1}\biggr)^{(s+1)(x_{0}+2)}\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{((x_{0}+3)D)^{(x_{0}+3)D}}{(x_{0}D)^{x_{0}D}}\frac{(x_{0}+1)^{(s+1)(x_{0}+1)}}{(x_{0}+2)^{(s+1)(x_{0}+2)}}\nonumber\\ \displaystyle & = & \displaystyle g(x_{0})f(x_{0})^{x_{0}}=g(x_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k_{0}(n),j}^{1/n} & {\sim} & \displaystyle \biggl(\frac{n}{e}\biggr)^{s+1-3D}\biggl(\frac{3Dn+Dk_{0}(n)+j}{e}\biggr)^{3D+Dx_{0}}\biggl(\frac{e}{Dk_{0}(n)+j-1}\biggr)^{Dx_{0}}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{n+k_{0}(n)+j/D}{e}\biggr)^{(s+1)(x_{0}+1)}\biggl(\frac{e}{2n+k_{0}(n)+j/D+1}\biggr)^{(s+1)(x_{0}+2)}\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{((x_{0}+3)D)^{(x_{0}+3)D}}{(x_{0}D)^{x_{0}D}}\frac{(x_{0}+1)^{(s+1)(x_{0}+1)}}{(x_{0}+2)^{(s+1)(x_{0}+2)}}\nonumber\\ \displaystyle & = & \displaystyle g(x_{0})f(x_{0})^{x_{0}}=g(x_{0}).\end{eqnarray}$$
We now show that the asymptotic behaviour of
![]() $r_{n,j}$
as
$r_{n,j}$
as
![]() $n\rightarrow \infty$
is determined by the terms
$n\rightarrow \infty$
is determined by the terms
![]() $c_{k,j}$
with
$c_{k,j}$
with
![]() $k$
close to
$k$
close to
![]() $x_{0}n$
. Given
$x_{0}n$
. Given
![]() $D$
and
$D$
and
![]() $s$
, we take
$s$
, we take
![]() $\unicode[STIX]{x1D700}>0$
sufficiently small to accommodate the condition
$\unicode[STIX]{x1D700}>0$
sufficiently small to accommodate the condition
Then there exists
![]() $A(\unicode[STIX]{x1D700})>x_{1}$
, where
$A(\unicode[STIX]{x1D700})>x_{1}$
, where
![]() $x_{1}$
is the unique positive root of
$x_{1}$
is the unique positive root of
![]() $f^{\prime }(x)=0$
, such that
$f^{\prime }(x)=0$
, such that
![]() $f(A(\unicode[STIX]{x1D700}))=b(\unicode[STIX]{x1D700})$
. We have
$f(A(\unicode[STIX]{x1D700}))=b(\unicode[STIX]{x1D700})$
. We have
![]() $f(x)\geqslant 1/b(\unicode[STIX]{x1D700})$
for any
$f(x)\geqslant 1/b(\unicode[STIX]{x1D700})$
for any
![]() $x\in (0,x_{0}\,-\,\unicode[STIX]{x1D700}]$
and
$x\in (0,x_{0}\,-\,\unicode[STIX]{x1D700}]$
and
![]() $f(x)\leqslant b(\unicode[STIX]{x1D700})$
for any
$f(x)\leqslant b(\unicode[STIX]{x1D700})$
for any
![]() $x\in [x_{0}\,+\,\unicode[STIX]{x1D700},A(\unicode[STIX]{x1D700})]$
. For any
$x\in [x_{0}\,+\,\unicode[STIX]{x1D700},A(\unicode[STIX]{x1D700})]$
. For any
![]() $k$
such that
$k$
such that
![]() $(x_{0}\,+\,2\unicode[STIX]{x1D700})n\leqslant k\leqslant (A(\unicode[STIX]{x1D700})\,-\,\unicode[STIX]{x1D700})n$
, Equation (3.3) and the sentence after imply that
$(x_{0}\,+\,2\unicode[STIX]{x1D700})n\leqslant k\leqslant (A(\unicode[STIX]{x1D700})\,-\,\unicode[STIX]{x1D700})n$
, Equation (3.3) and the sentence after imply that
![]() $c_{k,j}\leqslant b(\unicode[STIX]{x1D700})c_{k-1,j}$
provided
$c_{k,j}\leqslant b(\unicode[STIX]{x1D700})c_{k-1,j}$
provided
![]() $n$
is large (in terms of
$n$
is large (in terms of
![]() $D$
,
$D$
,
![]() $s$
and
$s$
and
![]() $\unicode[STIX]{x1D700}$
), so that, taking
$\unicode[STIX]{x1D700}$
), so that, taking
![]() $k_{1}=\lfloor (x_{0}\,+\,2\unicode[STIX]{x1D700})n\rfloor$
and
$k_{1}=\lfloor (x_{0}\,+\,2\unicode[STIX]{x1D700})n\rfloor$
and
![]() $k_{2}=\lfloor (x_{0}\,+\,3\unicode[STIX]{x1D700})n\rfloor$
, we obtain
$k_{2}=\lfloor (x_{0}\,+\,3\unicode[STIX]{x1D700})n\rfloor$
, we obtain
for all
![]() $n$
sufficiently large. In the same way, we get the estimate
$n$
sufficiently large. In the same way, we get the estimate
for all
![]() $n$
large (in terms of
$n$
large (in terms of
![]() $D$
,
$D$
,
![]() $s$
and
$s$
and
![]() $\unicode[STIX]{x1D700}$
). Finally, choosing
$\unicode[STIX]{x1D700}$
). Finally, choosing
![]() $\unicode[STIX]{x1D700}$
small, we can assume that
$\unicode[STIX]{x1D700}$
small, we can assume that
![]() $A(\unicode[STIX]{x1D700})$
is sufficiently large (in terms of
$A(\unicode[STIX]{x1D700})$
is sufficiently large (in terms of
![]() $D$
and
$D$
and
![]() $s$
), so that for
$s$
), so that for
![]() $k\geqslant (A(\unicode[STIX]{x1D700})\,-\,\unicode[STIX]{x1D700})n$
we have
$k\geqslant (A(\unicode[STIX]{x1D700})\,-\,\unicode[STIX]{x1D700})n$
we have
for
![]() $n$
large. Combining this result with the estimate
$n$
large. Combining this result with the estimate
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil }^{+\infty }\frac{1}{k^{(n+1)(s+1-3D)}} & {\leqslant} & \displaystyle \frac{1}{\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil ^{(n+1)(s+1-3D)-2}}\mathop{\sum }_{k=\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil }^{+\infty }\frac{1}{k^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2}{\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil ^{(n+1)(s+1-3D)-2}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil }^{+\infty }\frac{1}{k^{(n+1)(s+1-3D)}} & {\leqslant} & \displaystyle \frac{1}{\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil ^{(n+1)(s+1-3D)-2}}\mathop{\sum }_{k=\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil }^{+\infty }\frac{1}{k^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2}{\lceil (A(\unicode[STIX]{x1D700})-\unicode[STIX]{x1D700})n\rceil ^{(n+1)(s+1-3D)-2}}\nonumber\end{eqnarray}$$
gives
Using hypothesis (3.1) and the Stirling formula, the latter estimate implies
provided
![]() $n$
is sufficiently large. For
$n$
is sufficiently large. For
![]() $\unicode[STIX]{x1D700}$
small, we can assume that
$\unicode[STIX]{x1D700}$
small, we can assume that
![]() $A(\unicode[STIX]{x1D700})$
is sufficiently large (in terms of
$A(\unicode[STIX]{x1D700})$
is sufficiently large (in terms of
![]() $D$
and
$D$
and
![]() $s$
) to obtain
$s$
) to obtain
Combining Equations (3.4)–(3.7), we deduce that
Now for any
![]() $k$
in the range
$k$
in the range
![]() $(x_{0}\,-\,3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}\,+\,3\unicode[STIX]{x1D700})n$
it follows from the proof of Equation (3.4) that
$(x_{0}\,-\,3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}\,+\,3\unicode[STIX]{x1D700})n$
it follows from the proof of Equation (3.4) that
for
![]() $n$
large (in terms of
$n$
large (in terms of
![]() $D$
,
$D$
,
![]() $s$
and
$s$
and
![]() $\unicode[STIX]{x1D700}$
), where
$\unicode[STIX]{x1D700}$
), where
![]() $h$
is a positive function of
$h$
is a positive function of
![]() $\unicode[STIX]{x1D700}$
such that
$\unicode[STIX]{x1D700}$
such that
![]() $\lim _{\unicode[STIX]{x1D700}\rightarrow 0^{+}}h(\unicode[STIX]{x1D700})=0$
. Using (3.8), this implies
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0^{+}}h(\unicode[STIX]{x1D700})=0$
. Using (3.8), this implies
for
![]() $n$
sufficiently large, and finishes the proof of
$n$
sufficiently large, and finishes the proof of
![]() $\lim _{n\rightarrow \infty }r_{n,j}^{1/n}=g(x_{0})$
for any
$\lim _{n\rightarrow \infty }r_{n,j}^{1/n}=g(x_{0})$
for any
![]() $j$
.
$j$
.
To establish
for any
![]() $j,j^{\prime }\in \{1,\ldots ,D\}$
, we can assume that
$j,j^{\prime }\in \{1,\ldots ,D\}$
, we can assume that
![]() $1\leqslant j\leqslant D\,-\,1$
and
$1\leqslant j\leqslant D\,-\,1$
and
![]() $j^{\prime }=j\,+\,1$
. For any
$j^{\prime }=j\,+\,1$
. For any
![]() $k$
we have
$k$
we have
It follows from the Stirling formula that
![]() $\unicode[STIX]{x1D6E4}(x\,+\,1/D)\sim x^{1/D}\unicode[STIX]{x1D6E4}(x)$
as
$\unicode[STIX]{x1D6E4}(x\,+\,1/D)\sim x^{1/D}\unicode[STIX]{x1D6E4}(x)$
as
![]() $x\rightarrow \infty$
, so that for
$x\rightarrow \infty$
, so that for
![]() $k=\lfloor x_{0}n\rfloor$
we have, as
$k=\lfloor x_{0}n\rfloor$
we have, as
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
More generally, for
![]() $k$
in the range
$k$
in the range
![]() $(x_{0}\,-\,3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}\,+\,3\unicode[STIX]{x1D700})n$
and
$(x_{0}\,-\,3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}\,+\,3\unicode[STIX]{x1D700})n$
and
![]() $n$
sufficiently large we have
$n$
sufficiently large we have
with
![]() $\lim _{\unicode[STIX]{x1D700}\rightarrow 0^{+}}\tilde{h}(\unicode[STIX]{x1D700})=0$
. Using Equation (3.8) twice, we deduce that
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0^{+}}\tilde{h}(\unicode[STIX]{x1D700})=0$
. Using Equation (3.8) twice, we deduce that
 $$\begin{eqnarray}\displaystyle r_{n,j+1} & {\leqslant} & \displaystyle \frac{1}{1-3\unicode[STIX]{x1D700}}\mathop{\sum }_{(x_{0}-3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}+3\unicode[STIX]{x1D700})n}c_{k,j+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1+\tilde{h}(\unicode[STIX]{x1D700})}{1-3\unicode[STIX]{x1D700}}\mathop{\sum }_{(x_{0}-3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}+3\unicode[STIX]{x1D700})n}c_{k,j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1+\tilde{h}(\unicode[STIX]{x1D700})}{1-3\unicode[STIX]{x1D700}}r_{n,j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{n,j+1} & {\leqslant} & \displaystyle \frac{1}{1-3\unicode[STIX]{x1D700}}\mathop{\sum }_{(x_{0}-3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}+3\unicode[STIX]{x1D700})n}c_{k,j+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1+\tilde{h}(\unicode[STIX]{x1D700})}{1-3\unicode[STIX]{x1D700}}\mathop{\sum }_{(x_{0}-3\unicode[STIX]{x1D700})n\leqslant k\leqslant (x_{0}+3\unicode[STIX]{x1D700})n}c_{k,j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1+\tilde{h}(\unicode[STIX]{x1D700})}{1-3\unicode[STIX]{x1D700}}r_{n,j}.\nonumber\end{eqnarray}$$
In the same way we obtain
Combining these inequalities and using that
![]() $\unicode[STIX]{x1D700}>0$
is arbitrary results in
$\unicode[STIX]{x1D700}>0$
is arbitrary results in
This concludes the proof of (3.2), except for the upper bound on
![]() $g(x_{0})$
which we verify now.
$g(x_{0})$
which we verify now.
To estimate
![]() $g(x_{0})$
from above, we can assume by (3.1) that the value
$g(x_{0})$
from above, we can assume by (3.1) that the value
is smaller than
![]() $1$
, so that
$1$
, so that
![]() $x_{0}<\frac{1}{2}$
. The logarithmic derivative of
$x_{0}<\frac{1}{2}$
. The logarithmic derivative of
![]() $g(x)$
is given by
$g(x)$
is given by
By the hypothesis (3.1), the function
![]() $g(x)$
is decreasing on the interval
$g(x)$
is decreasing on the interval
![]() $[0,\frac{1}{2}]$
. We deduce that
$[0,\frac{1}{2}]$
. We deduce that
where (3.1) was used again. This completes our proof of Lemma 3. ◻
Remark 3. For
![]() $s=77$
and
$s=77$
and
![]() $D=4$
one computes
$D=4$
one computes
![]() $g(x_{0})<\exp (-78)$
. Thus, the suitable linear combinations (cf. § 5)
$g(x_{0})<\exp (-78)$
. Thus, the suitable linear combinations (cf. § 5)
of the corresponding linear forms allow us to eliminate three of the odd zeta values from the list
In particular, we obtain that two out of
![]() $\{\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(77)\}$
are irrational. This result is slightly weaker than the result of Rivoal and the third author [Reference Rivoal and ZudilinRZ18], but it emerges as a byproduct of the construction above. The arithmetic gain given by
$\{\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\ldots ,\unicode[STIX]{x1D701}(77)\}$
are irrational. This result is slightly weaker than the result of Rivoal and the third author [Reference Rivoal and ZudilinRZ18], but it emerges as a byproduct of the construction above. The arithmetic gain given by
![]() $\unicode[STIX]{x1D6F7}_{n}(4)$
for
$\unicode[STIX]{x1D6F7}_{n}(4)$
for
![]() $\unicode[STIX]{x1D6F7}_{n}(D)$
defined in Remark 2 can be used to slightly reduce the bound of
$\unicode[STIX]{x1D6F7}_{n}(D)$
defined in Remark 2 can be used to slightly reduce the bound of
![]() $77$
to
$77$
to
![]() $73$
, still weaker than that in [Reference Rivoal and ZudilinRZ18].
$73$
, still weaker than that in [Reference Rivoal and ZudilinRZ18].
4 A non-vanishing determinant
The following lemma is used to eliminate irrational zeta values in § 5 below.
Lemma 4. For
![]() $t\geqslant 1$
, let
$t\geqslant 1$
, let
![]() $x_{1}<\cdots <x_{t}$
be positive real numbers and
$x_{1}<\cdots <x_{t}$
be positive real numbers and
![]() $\unicode[STIX]{x1D6FC}_{1}<\cdots <\unicode[STIX]{x1D6FC}_{t}$
non-negative integers. Then the generalized Vandermonde matrix
$\unicode[STIX]{x1D6FC}_{1}<\cdots <\unicode[STIX]{x1D6FC}_{t}$
non-negative integers. Then the generalized Vandermonde matrix
![]() $[x_{j}^{\unicode[STIX]{x1D6FC}_{i}}]_{1\leqslant i,j\leqslant t}$
has positive determinant.
$[x_{j}^{\unicode[STIX]{x1D6FC}_{i}}]_{1\leqslant i,j\leqslant t}$
has positive determinant.
We remark that, subject to the hypothesis that
![]() $x_{1},\ldots ,x_{t}$
are real and positive, Lemma 4 is a stronger version of [Reference Laurent, Mignotte and NesterenkoLMN95, Lemme 1] and, therefore, has potential applications to the zero estimates for linear forms in two logarithms.
$x_{1},\ldots ,x_{t}$
are real and positive, Lemma 4 is a stronger version of [Reference Laurent, Mignotte and NesterenkoLMN95, Lemme 1] and, therefore, has potential applications to the zero estimates for linear forms in two logarithms.
The above result is quite classical and known to many people. While writing this paper we found various proofs of rather different nature, three given below. We leave it to the reader to choose their favourite proof.
Combinatorial proof of Lemma 4.
As pointed out in [Reference KrattenthalerKra99, § 2.1], the generalized Vandermonde determinant in question is closely related to Schur polynomials. Let
![]() $\unicode[STIX]{x1D6E5}:=\det [x_{j}^{\unicode[STIX]{x1D6FC}_{i}}]_{1\leqslant i,j\leqslant t}$
, and
$\unicode[STIX]{x1D6E5}:=\det [x_{j}^{\unicode[STIX]{x1D6FC}_{i}}]_{1\leqslant i,j\leqslant t}$
, and
be the Vandermonde determinant of
![]() $x_{1},\ldots ,x_{t}$
. For any
$x_{1},\ldots ,x_{t}$
. For any
![]() $i\in \{1,\ldots ,t\}$
, we take
$i\in \{1,\ldots ,t\}$
, we take
![]() $\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FC}_{t+1-i}+i-t$
, so that
$\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FC}_{t+1-i}+i-t$
, so that
![]() $\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{t}\geqslant 0$
; then
$\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{t}\geqslant 0$
; then
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{t})$
is a partition of the integer
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{t})$
is a partition of the integer
![]() $\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{t}$
. The associated Schur polynomial
$\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{t}$
. The associated Schur polynomial
possesses the expression
with the sum over all column-strict Young tableaux
![]() $T$
of shape
$T$
of shape
![]() $\unicode[STIX]{x1D706}$
(see, for instance, [Reference Fulton and HarrisFH91, Appendix A, A.31] or [Reference MacdonaldMac79, I.3], and [Reference ProctorPro89] for a direct proof). Here,
$\unicode[STIX]{x1D706}$
(see, for instance, [Reference Fulton and HarrisFH91, Appendix A, A.31] or [Reference MacdonaldMac79, I.3], and [Reference ProctorPro89] for a direct proof). Here,
![]() $m_{i}(T)$
denotes the number of occurrences of
$m_{i}(T)$
denotes the number of occurrences of
![]() $i$
in the tableau
$i$
in the tableau
![]() $T$
. From this we deduce that
$T$
. From this we deduce that
![]() $s_{\unicode[STIX]{x1D706}}$
is a positive real number, thus
$s_{\unicode[STIX]{x1D706}}$
is a positive real number, thus
![]() $\unicode[STIX]{x1D6E5}=s_{\unicode[STIX]{x1D706}}\cdot V>0$
.◻
$\unicode[STIX]{x1D6E5}=s_{\unicode[STIX]{x1D706}}\cdot V>0$
.◻
Linear algebra proof of Lemma 4.
Write
![]() $A_{J,K}$
for the minor of an
$A_{J,K}$
for the minor of an
![]() $n\,\times \,m$
matrix
$n\,\times \,m$
matrix
![]() $A$
, where
$A$
, where
![]() $n\leqslant m$
, determined by ordered index sets
$n\leqslant m$
, determined by ordered index sets
![]() $J$
and
$J$
and
![]() $K$
. A classical result due to Fekete [Reference Fekete and PólyaFP12] asserts that if all
$K$
. A classical result due to Fekete [Reference Fekete and PólyaFP12] asserts that if all
![]() $(n\,-\,1)$
-minors
$(n\,-\,1)$
-minors
are positive, and all minors of size
![]() $n$
with consecutive columns are positive, then all
$n$
with consecutive columns are positive, then all
![]() $n$
-minors of
$n$
-minors of
![]() $A$
are positive. Thus, Lemma 4 follows by induction on
$A$
are positive. Thus, Lemma 4 follows by induction on
![]() $t$
from Fekete’s result applied to the matrix
$t$
from Fekete’s result applied to the matrix
![]() $[x_{j}^{k}]_{1\leqslant j\leqslant t,\,0\leqslant k<m}$
, using the positivity of the Vandermonde determinant.◻
$[x_{j}^{k}]_{1\leqslant j\leqslant t,\,0\leqslant k<m}$
, using the positivity of the Vandermonde determinant.◻
Analytical proof of Lemma 4 (see [Reference Gantmacher and KreinGK02, pp. 76–77]).
By induction on
![]() $t$
one proves the following claim. A non-zero function
$t$
one proves the following claim. A non-zero function
with
![]() $c_{i},\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}$
, has at most
$c_{i},\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}$
, has at most
![]() $t\,-\,1$
positive zeros. Indeed, if
$t\,-\,1$
positive zeros. Indeed, if
![]() $f$
has
$f$
has
![]() $t$
positive zeros then Rolle’s theorem provides
$t$
positive zeros then Rolle’s theorem provides
![]() $t\,-\,1$
positive zeros of the derivative
$t\,-\,1$
positive zeros of the derivative
![]() $(\text{d}/\text{d}x)(x^{-\unicode[STIX]{x1D6FC}_{1}}f(x))$
. The non-vanishing of the determinant in Lemma 4 is an immediate consequence of this claim. Since the determinant depends continuously on the parameters
$(\text{d}/\text{d}x)(x^{-\unicode[STIX]{x1D6FC}_{1}}f(x))$
. The non-vanishing of the determinant in Lemma 4 is an immediate consequence of this claim. Since the determinant depends continuously on the parameters
![]() $\unicode[STIX]{x1D6FC}_{i}$
, we deduce the required positivity from the positivity of the Vandermonde determinant.◻
$\unicode[STIX]{x1D6FC}_{i}$
, we deduce the required positivity from the positivity of the Vandermonde determinant.◻
5 Elimination of odd zeta values
Let
![]() $0<\unicode[STIX]{x1D700}<\frac{1}{3}$
, and let
$0<\unicode[STIX]{x1D700}<\frac{1}{3}$
, and let
![]() $s$
be odd and sufficiently large with respect to
$s$
be odd and sufficiently large with respect to
![]() $\unicode[STIX]{x1D700}$
. We take
$\unicode[STIX]{x1D700}$
. We take
![]() $D$
to be the product of all primes less than or equal to
$D$
to be the product of all primes less than or equal to
![]() $(1\,-\,2\unicode[STIX]{x1D700})\log s$
(such a product has asymptotically the largest possible number of divisors with respect to its size; see [Reference Hardy and WrightHW79, ch. XVIII, § 1]). We have
$(1\,-\,2\unicode[STIX]{x1D700})\log s$
(such a product has asymptotically the largest possible number of divisors with respect to its size; see [Reference Hardy and WrightHW79, ch. XVIII, § 1]). We have
by the prime number theorem, that is,
![]() $D\leqslant s^{1-\unicode[STIX]{x1D700}}$
. Then
$D\leqslant s^{1-\unicode[STIX]{x1D700}}$
. Then
![]() $D\log D\leqslant s^{1-\unicode[STIX]{x1D700}}\log s$
: the assumption of Lemma 3 holds.
$D\log D\leqslant s^{1-\unicode[STIX]{x1D700}}\log s$
: the assumption of Lemma 3 holds.
Notice that
![]() $D$
has precisely
$D$
has precisely
![]() $\unicode[STIX]{x1D6FF}=2^{\unicode[STIX]{x1D70B}((1-2\unicode[STIX]{x1D700})\log s)}$
divisors, with
$\unicode[STIX]{x1D6FF}=2^{\unicode[STIX]{x1D70B}((1-2\unicode[STIX]{x1D700})\log s)}$
divisors, with
Assume that the number of irrational odd zeta values between
![]() $\unicode[STIX]{x1D701}(3)$
and
$\unicode[STIX]{x1D701}(3)$
and
![]() $\unicode[STIX]{x1D701}(s)$
is less than or equal to
$\unicode[STIX]{x1D701}(s)$
is less than or equal to
![]() $\unicode[STIX]{x1D6FF}\,-\,1$
. Let
$\unicode[STIX]{x1D6FF}\,-\,1$
. Let
![]() $3=i_{1}<i_{2}<\cdots <i_{\unicode[STIX]{x1D6FF}-1}\leqslant s$
be odd integers such that if
$3=i_{1}<i_{2}<\cdots <i_{\unicode[STIX]{x1D6FF}-1}\leqslant s$
be odd integers such that if
![]() $\unicode[STIX]{x1D701}(i)\not \in \mathbb{Q}$
and
$\unicode[STIX]{x1D701}(i)\not \in \mathbb{Q}$
and
![]() $i$
is odd,
$i$
is odd,
![]() $3\leqslant i\leqslant s$
, then
$3\leqslant i\leqslant s$
, then
![]() $i=i_{j}$
for some
$i=i_{j}$
for some
![]() $j$
. We set
$j$
. We set
![]() $i_{0}=1$
, and consider the set
$i_{0}=1$
, and consider the set
![]() ${\mathcal{D}}$
of all divisors of
${\mathcal{D}}$
of all divisors of
![]() $D$
, so that
$D$
, so that
![]() $\operatorname{Card}{\mathcal{D}}=\unicode[STIX]{x1D6FF}$
. Lemma 4 implies that the matrix
$\operatorname{Card}{\mathcal{D}}=\unicode[STIX]{x1D6FF}$
. Lemma 4 implies that the matrix
![]() $[d^{i_{j}}]_{d\in {\mathcal{D}},0\leqslant j\leqslant \unicode[STIX]{x1D6FF}-1}$
is invertible. Therefore, there exist integers
$[d^{i_{j}}]_{d\in {\mathcal{D}},0\leqslant j\leqslant \unicode[STIX]{x1D6FF}-1}$
is invertible. Therefore, there exist integers
![]() $w_{d}\in \mathbb{Z}$
, where
$w_{d}\in \mathbb{Z}$
, where
![]() $d\in {\mathcal{D}}$
, such that
$d\in {\mathcal{D}}$
, such that
and
With the help of Lemma 1 we construct the linear forms
 $$\begin{eqnarray}r_{n,j}=\unicode[STIX]{x1D70C}_{0,j}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}\unicode[STIX]{x1D701}\biggl(i,\frac{j}{D}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}r_{n,j}=\unicode[STIX]{x1D70C}_{0,j}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}\unicode[STIX]{x1D701}\biggl(i,\frac{j}{D}\biggr)\end{eqnarray}$$
for
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $1\leqslant j\leqslant D$
. The crucial point (as in [Reference SprangSpr18, § 3]) is that for any
$1\leqslant j\leqslant D$
. The crucial point (as in [Reference SprangSpr18, § 3]) is that for any
![]() $d\in {\mathcal{D}}$
and any
$d\in {\mathcal{D}}$
and any
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
implying that
 $$\begin{eqnarray}\widehat{r}_{n,d}=\mathop{\sum }_{j=1}^{d}r_{n,jD/d}=\mathop{\sum }_{j=1}^{d}\unicode[STIX]{x1D70C}_{0,jD/d}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}d^{i}\unicode[STIX]{x1D701}(i)\end{eqnarray}$$
$$\begin{eqnarray}\widehat{r}_{n,d}=\mathop{\sum }_{j=1}^{d}r_{n,jD/d}=\mathop{\sum }_{j=1}^{d}\unicode[STIX]{x1D70C}_{0,jD/d}+\mathop{\sum }_{\substack{ 3\leqslant i\leqslant s \\ i\;\text{odd}}}\unicode[STIX]{x1D70C}_{i}d^{i}\unicode[STIX]{x1D701}(i)\end{eqnarray}$$
are linear forms in the odd zeta values with asymptotic behaviour
by Lemma 3.
We now use the integers
![]() $w_{d}$
to eliminate the odd zeta values
$w_{d}$
to eliminate the odd zeta values
![]() $\unicode[STIX]{x1D701}(i_{j})$
for
$\unicode[STIX]{x1D701}(i_{j})$
for
![]() $j=1,\ldots ,\unicode[STIX]{x1D6FF}\,-\,1$
, including all irrational ones, as in [Reference ZudilinZud18, Reference SprangSpr18]. For that purpose, consider
$j=1,\ldots ,\unicode[STIX]{x1D6FF}\,-\,1$
, including all irrational ones, as in [Reference ZudilinZud18, Reference SprangSpr18]. For that purpose, consider
Equations (5.1) imply that
where
![]() $I=\{3,5,7,\ldots ,s\}\setminus \{i_{1},\ldots ,i_{\unicode[STIX]{x1D6FF}-1}\}$
; in particular, no irrational zeta value
$I=\{3,5,7,\ldots ,s\}\setminus \{i_{1},\ldots ,i_{\unicode[STIX]{x1D6FF}-1}\}$
; in particular, no irrational zeta value
![]() $\unicode[STIX]{x1D701}(i)$
, where
$\unicode[STIX]{x1D701}(i)$
, where
![]() $3\leqslant i\leqslant s$
, appears in this linear combination. Using Equation (5.2), we obtain
$3\leqslant i\leqslant s$
, appears in this linear combination. Using Equation (5.2), we obtain
so that
Now all
![]() $\unicode[STIX]{x1D701}(i)$
,
$\unicode[STIX]{x1D701}(i)$
,
![]() $i\in I$
, are assumed to be rational. Denoting by
$i\in I$
, are assumed to be rational. Denoting by
![]() $A$
their common denominator, we deduce from Lemma 2 that
$A$
their common denominator, we deduce from Lemma 2 that
![]() $Ad_{n+1}^{s+1}\widetilde{r}_{n}$
is an integer. From the prime number theorem we have
$Ad_{n+1}^{s+1}\widetilde{r}_{n}$
is an integer. From the prime number theorem we have
![]() $\lim _{n\rightarrow \infty }d_{n+1}^{1/n}=e$
, hence the sequence of integers satisfies
$\lim _{n\rightarrow \infty }d_{n+1}^{1/n}=e$
, hence the sequence of integers satisfies
This contradiction concludes the proof of Theorem 2.
Acknowledgements
We thank Michel Waldschmidt for his advice, Ole Warnaar for his comments on an earlier draft of the paper, and Javier Fresán for educating us about the state of the art in Grothendieck’s period conjecture and its consequences. We are indebted to the referees, including the referee for [Reference Fischler, Sprang and ZudilinFSZ18], for several useful remarks.