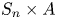Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T17:55:04.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Malle's conjecture for $S_n\times A$ for 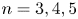$n = 3,4,5$

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  15 February 2021

Jiuya Wang
Jiuya Wang*
Affiliation:
Department of Mathematics, Duke University, 120 Science Drive, 117 Physics Building, Durham, NC27708, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a framework to prove Malle's conjecture for the compositum of two number fields based on proven results of Malle's conjecture and good uniformity estimates. Using this method, we prove Malle's conjecture for 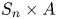$S_n\times A$ over any number field 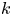$k$ for 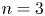$n=3$ with 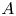$A$ an abelian group of order relatively prime to 2, for 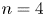$n= 4$ with 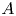$A$ an abelian group of order relatively prime to 6, and for 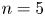$n=5$ with 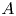$A$ an abelian group of order relatively prime to 30. As a consequence, we prove that Malle's conjecture is true for 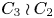$C_3\wr C_2$ in its 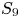$S_9$ representation, whereas its 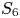$S_6$ representation is the first counter-example of Malle's conjecture given by Klüners. We also prove new local uniformity results for ramified 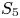$S_5$ quintic extensions over arbitrary number fields by adapting Bhargava's geometric sieve and averaging over fundamental domains of the parametrization space.

Keywords

Malle's conjecturecompositumuniformity estimatecounter exampledensity of discriminants

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants 11R45: Density theorems
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 1 , January 2021 , pp. 83 - 121
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belabas, K., Bhargava, M. and Pomerance, C., Error terms for the Davenport-Heilbronn theorems, Duke Math. J. 153 (2010), 173–210.10.1215/00127094-2010-007CrossRefGoogle Scholar
Belabas, K. and Fouvry, E., Discriminants cubiques et progressions arithmétiques, Int. J. Number Theory 6 (2010), 1491–1529.10.1142/S1793042110003605CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quartic rings and fields, Ann. Math. (2) 162 (2005), 1031–1063.10.4007/annals.2005.162.1031CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quintic rings and fields, Ann. Math. (2) 172 (2010), 1559–1591.10.4007/annals.2010.172.1559CrossRefGoogle Scholar
Bhargava, M., The geometric sieve and the density of squarefree values of polynomial discriminants and other invariant polynomials, Preprint (2014), arXiv:1402.0031.Google Scholar
Bhargava, M., Shankar, A. and Tsimerman, J., On the Davenport-Heilbronn theorems and second order terms, Invent. Math. 193 (2013), 439–499.10.1007/s00222-012-0433-0CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X., Geometry-of-numbers methods over global fields I: Prehomogeneous vector spaces, Preprint (2015), arXiv:1512.03035.Google Scholar
Bhargava, M. and Wood, M. M., The density of discriminants of ${S}_3$-sextic number fields, Proc. Amer. Math. Soc. 136 (2008), 1581–1587.10.1090/S0002-9939-07-09171-XCrossRefGoogle Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., Enumerating quartic dihedral extensions of $\mathbb {Q}$, Compos. Math. 133 (2002), 65–93.10.1023/A:1016310902973CrossRefGoogle Scholar
Datskovsky, B. and Wright, D. J., Density of discriminants of cubic extensions, J. Reine Angew. Math. 386 (1988), 116–138.Google Scholar
Davenport, H. and Heilbronn, H., On the density of discriminants of cubic fields. II, Proc. R. Soc. Lond. Ser. A 322 (1971), 405–420.Google Scholar
Klüners, J., A counter example to Malle's conjecture on the asymptotics of discriminants, C. R. Math. Acad. Sci. Paris 340 (2005), 411–414.10.1016/j.crma.2005.02.010CrossRefGoogle Scholar
Klüners, J., Über die Asymptotik von Zahlkörpern mit vorgegebener Galoisgruppe (Shaker Verlag, 2005).Google Scholar
Klüners, J., The distribution of number fields with wreath products as Galois groups, Int. J. Number Theory 8 (2012), 845–858.10.1142/S1793042112500492CrossRefGoogle Scholar
Klüners, J. and Malle, G., Counting nilpotent Galois extensions, J. Reine Angew. Math. 572 (2004), 1–26.10.1515/crll.2004.050CrossRefGoogle Scholar
Lang, S., Algebraic number theory, Graduate Texts in Mathematics, vol. 110 (Springer, 1994).10.1007/978-1-4612-0853-2CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and modular forms database (2013), http://www.lmfdb.org.Google Scholar
Mäki, S., On the density of abelian number fields, Ann. Acad. Sci. Fenn. Diss. Series A I. Mathematica Dissertationes, vol. 54 (Suomalainen Tiedeakatemia, Helsinki, 1985).Google Scholar
Malle, G., On the distribution of Galois groups, J. Number Theory 92 (2002), 315–329.10.1006/jnth.2001.2713CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory I: Classical theory, Cambridge Studies in Advanced Mathematics (Cambridge University Press, 2006).10.1017/CBO9780511618314CrossRefGoogle Scholar
Narkiewicz, W., Number theory (World Scientific, 1983).Google Scholar
Neukirch, J., Algebraic number theory, vol. 322 (Springer, 1999).10.1007/978-3-662-03983-0CrossRefGoogle Scholar
Poonen, B., Squarefree values of multivariable polynomials, Duke Math. J. 118 (2003), 353–373.10.1215/S0012-7094-03-11826-8CrossRefGoogle Scholar
Shankar, A. and Tsimerman, J., Counting ${S}_5$-fields with a power saving error term, Forum Math. Sigma 2 (2014), e13.10.1017/fms.2014.10CrossRefGoogle Scholar
Taniguchi, T. and Thorne, F., Secondary terms in counting functions for cubic fields, Duke Math. J. 162 (2013), 2451–2508.10.1215/00127094-2371752CrossRefGoogle Scholar
Turkelli, S., Connected components of Hurwitz schemes and Malle's conjecture, Preprint (2008), arXiv:0809.0951.Google Scholar
Whittaker, E. T. and Watson, G. N., A course of modern analysis (Cambridge University Press, 1996).10.1017/CBO9780511608759CrossRefGoogle Scholar
Wood, M. M., On the probabilities of local behaviors in Abelian field extensions, Compos. Math. 146 (2010), 102–128.10.1112/S0010437X0900431XCrossRefGoogle Scholar
Wood, M. M., Asymptotics for number fields and class groups, in Directions in number theory (Springer, 2016), 291–339.10.1007/978-3-319-30976-7_10CrossRefGoogle Scholar
Wright, D. J., Distribution of discriminants of Abelian extensions, Proc. Lond. Math. Soc. (3) 58 (1989), 1300–1320.Google Scholar