Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T03:11:36.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Log canonical pairs with good augmented base loci

Part of: Birational geometry

Published online by Cambridge University Press:  26 March 2014

Caucher Birkar  and
Zhengyu Hu
Caucher Birkar
Affiliation:
DPMMS, Centre for Mathematical Sciences, Cambridge University, Wilberforce Road, Cambridge, CB3 0WB, UK email [email protected]
Zhengyu Hu
Affiliation:
DPMMS, Centre for Mathematical Sciences, Cambridge University, Wilberforce Road, Cambridge, CB3 0WB, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 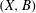$(X,B)$ be a projective log canonical pair such that 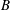$B$ is a 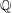$\mathbb{Q}$-divisor, and that there is a surjective morphism 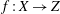$f: X\to Z$ onto a normal variety 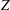$Z$ satisfying 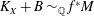$K_X+B\sim _{\mathbb{Q}} f^*M$ for some big 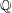$\mathbb{Q}$-divisor 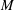$M$, and the augmented base locus 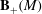${\mathbf{B}}_+(M)$ does not contain the image of any log canonical centre of 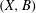$(X,B)$. We will show that 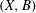$(X,B)$ has a good log minimal model. An interesting special case is when 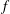$f$ is the identity morphism.

Keywords

minimal modelslog canonical ringsaugmented base loci

MSC classification

Secondary: 14E30: Minimal model program (Mori theory, extremal rays)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 4 , April 2014 , pp. 579 - 592
Copyright
© The Author(s) 2014 

References

Ambro, F., The moduli b-divisor of an lc-trivial fibration, Compositio Math. 141 (2005), 385–403.CrossRefGoogle Scholar
Birkar, C., On existence of log minimal models, Compositio Math. 146 (2010), 919–928.CrossRefGoogle Scholar
Birkar, C., Existence of log canonical flips and a special LMMP, Publ. Math. Inst. Hautes Études Sci. 115 (2012), 325–368.Google Scholar
Birkar, C., Cascini, P., Hacon, C. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.Google Scholar
Birkar, C. and Hu, Z., Polarized pairs, log minimal models, and Zariski decompositions, Nagoya Math. J., to appear; this is essentially arXiv:1302.4015 but with a different title.Google Scholar
Cacciola, S., On the semiampleness of the positive part of CKM Zariski decompositions, Math. Proc. Camb. Phil. Soc. 156 (2014), 1–23.Google Scholar
Fujino, O., Special termination and reduction to pl flips, in Flips for 3-folds and 4-folds, ed. A. Corti (Oxford University Press, Oxford, 2007).Google Scholar
Fujino, O. and Gongyo, Y., Log pluricanonical representations and abundance conjecture, Compositio Math., to appear, arXiv:1104.0361v3.Google Scholar
Fujino, O. and Gongyo, Y., On canonical bundle formulas and subadjunctions, Michigan Math. J. 61 (2012), 255–264.Google Scholar
Fujino, O. and Gongyo, Y., On log canonical rings, to appear in the proceedings of Kawamata’s 60th birthday conference. Preprint (2013), arXiv:1302.5194v2.Google Scholar
Gongyo, Y. and Lehmann, B., Reduction maps and minimal model theory, Compositio Math. 149 (2013), 295–308.Google Scholar
Hacon, C. D., McKernan, J. and Xu, C., ACC for log canonical thresholds, Ann. of Math. (2), to appear, arXiv:1208.4150v1.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties (Cambridge University Press, Cambridge, 1998).Google Scholar
Shokurov, V. V., Prelimiting flips, Proc. Steklov Inst. Math. 240 (2003), 75–213.Google Scholar