Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Isik, Mehmet Umut
2013.
Equivalence of the Derived Category of a Variety with a Singularity Category.
International Mathematics Research Notices,
Vol. 2013,
Issue. 12,
p.
2787.
Mirković, Ivan
and
Riche, Simon
2015.
Iwahori–Matsumoto Involution and Linear Koszul Duality.
International Mathematics Research Notices,
Vol. 2015,
Issue. 1,
p.
150.
Arinkin, D.
and
Gaitsgory, D.
2015.
Singular support of coherent sheaves and the geometric Langlands conjecture.
Selecta Mathematica,
Vol. 21,
Issue. 1,
p.
1.
Bezrukavnikov, Roman
2016.
On two geometric realizations of an affine Hecke algebra.
Publications mathématiques de l'IHÉS,
Vol. 123,
Issue. 1,
p.
1.
Mirković, I.
and
Riche, S.
2016.
Linear Koszul duality, II: coherent sheaves on perfect sheaves.
Journal of the London Mathematical Society,
Vol. 93,
Issue. 1,
p.
1.
Achar, Pramod N.
and
Riche, Simon
2016.
Modular perverse sheaves on flag varieties, II: Koszul duality and formality.
Duke Mathematical Journal,
Vol. 165,
Issue. 1,
Achar, Pramod N.
and
Riche, Simon
2018.
Reductive groups, the loop Grassmannian, and the Springer resolution.
Inventiones mathematicae,
Vol. 214,
Issue. 1,
p.
289.
Ballard, Matthew
Favero, David
and
Katzarkov, Ludmil
2019.
Variation of geometric invariant theory quotients and derived categories.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 746,
p.
235.
Vezzosi, Gabriele
2020.
Basic structures on derived critical loci.
Differential Geometry and its Applications,
Vol. 71,
Issue. ,
p.
101635.
Rennemo, Jørgen Vold
2020.
The homological projective dual of .
Compositio Mathematica,
Vol. 156,
Issue. 3,
p.
476.
Braverman, Alexander
Finkelberg, Michael
Ginzburg, Victor
and
Travkin, Roman
2021.
Mirabolic Satake equivalence and supergroups.
Compositio Mathematica,
Vol. 157,
Issue. 8,
p.
1724.
Toda, Yukinobu
2024.
Categorical Donaldson-Thomas Theory for Local Surfaces.
Vol. 2350,
Issue. ,
p.
1.
Toda, Yukinobu
2024.
Categorical Donaldson-Thomas Theory for Local Surfaces.
Vol. 2350,
Issue. ,
p.
129.
Zhao, Yu
2025.
A note on the categorical resolution of an effective Cartier divisor.
Journal of Algebra,
Vol. 672,
Issue. ,
p.
1.


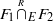 , and the corresponding derived intersection
, and the corresponding derived intersection 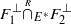 . We also propose applications to Hecke algebras.
. We also propose applications to Hecke algebras.