Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T01:14:24.598Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting of characters on p-adic orthogonal and metaplectic groups

Part of: Lie groups

Published online by Cambridge University Press:  18 March 2010

Tatiana K. Howard
Tatiana K. Howard*
Affiliation:
Mathematics Department, University of Michigan, Ann Arbor, MI 48109, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a p-adic field. Consider a dual pair 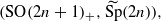where SO(2n+1)+ is the split orthogonal group and 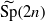is the metaplectic cover of the symplectic group Sp(2n) over F. We study lifting of characters between orthogonal and metaplectic groups. We say that a representation of SO(2n+1)+ lifts to a representation of 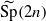if their characters on corresponding conjugacy classes are equal up to a transfer factor. We study properties of this transfer factor, which is essentially the character of the difference of the two halves of the oscillator representation. We show that the lifting commutes with parabolic induction. These results were motivated by the paper ‘Lifting of characters on orthogonal and metaplectic groups’ by Adams who considered the case F=ℝ.

Keywords

lifting of characterstransfer factoroscillator representationparabolic induction

MSC classification

Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 146 , Issue 3 , May 2010 , pp. 795 - 810
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Adams, J., Lifting of characters on orthogonal and metaplectic groups, Duke Math. J. 92 (1998), 129–178.CrossRefGoogle Scholar
[2]Adams, J. and Barbasch, D., Genuine representations of the metaplectic group, Compositio Math. 113 (1998), 23–66.CrossRefGoogle Scholar
[3]Howe, R. E., On the character of Weil’s representation, Trans. Amer. Math. Soc. 177 (1973), 287–298.Google Scholar
[4]Lion, G. and Vergne, M., The Weil representation, Maslov index and theta series, Progress in Mathematics, vol. 6 (Birkhäuser, Boston, 1980).CrossRefGoogle Scholar
[5]Maktouf, K., Le caractère de la représentation métaplectique et la formule du caractère pour certaines représentations d’un groupe de Lie presque algébrique sur un corps p-adique, J. Funct. Anal. 164 (1999), 249–339.CrossRefGoogle Scholar
[6]Raghunathan, M. S., Tori in quasi-split-groups, J. Ramanujan Math. Soc. 19 (2004), 281–287.Google Scholar
[7]Rao, R., On some explicit formulas in the theory of Weil representation, Pacific J. Math. 157 (1993), 335–371.Google Scholar
[8]Schultz, J., Lifting of characters of and SO 1,2(F) for F a nonarchemedean local field, PhD thesis, University of Maryland (1998).Google Scholar
[9]Shelstad, D., L-indistinguishability for real groups, Math. Ann. 259 (1982), 385–430.CrossRefGoogle Scholar
[10]Thomas, T., The character of the Weil representation, J. Lond. Math. Soc. 77 (2008), 221–239.CrossRefGoogle Scholar
[11]Van Dijk, G., Computation of certain induced characters of p-adic groups, Math. Ann. 199 (1972), 229–240.CrossRefGoogle Scholar