Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:49:32.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Level-raising for Saito–Kurokawa forms

Part of: Forms and linear algebraic groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 July 2009

Claus M. Sorensen
Claus M. Sorensen*
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper provides congruences between unstable and stable automorphic forms for the symplectic similitude group GSp(4). More precisely, we raise the level of certain CAP representations Π arising from classical modular forms. We first transfer Π to π on a suitable inner form G; this is achieved by θ-lifting. For π, we prove a precise level-raising result that is inspired by the work of Bellaiche and Clozel and which relies on computations of Schmidt. We thus obtain a 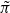congruent to π, with a local component that is irreducibly induced from an unramified twist of the Steinberg representation of the Klingen parabolic. To transfer 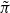back to GSp(4), we use Arthur’s stable trace formula. Since 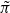has a local component of the above type, all endoscopic error terms vanish. Indeed, by results due to Weissauer, we only need to show that such a component does not participate in the θ-correspondence with any GO(4); this is an exercise in using Kudla’s filtration of the Jacquet modules of the Weil representation. We therefore obtain a cuspidal automorphic representation 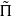of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for 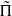to have vectors fixed by the non-special maximal compact subgroups at all primes dividing N. Since G is necessarily ramified at some prime r, we have to show a non-special analogue of the fundamental lemma at r. Finally, we give an application of our main result to the Bloch–Kato conjecture, assuming a conjecture of Skinner and Urban on the rank of the monodromy operators at the primes dividing N.

Keywords

automorphic formslevel-raising congruencestrace formulaSelmer groups

MSC classification

Secondary: 11E57: Classical groups 11E72: Galois cohomology of linear algebraic groups 11F27: Theta series; Weil representation; theta correspondences 11F33: Congruences for modular and $p$-adic modular forms 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 4 , July 2009 , pp. 915 - 953
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Arthur, J., On local character relations, Selecta Math. 2 (1996), 501–579.CrossRefGoogle Scholar
[2]Arthur, J., Towards a stable trace formula, in Proceedings of the international congress of mathematicians (Berlin, 1998), vol. II, Doc. Math., extra vol. ICM II1998, 507–517.CrossRefGoogle Scholar
[3]Bellaiche, J., Congruences endoscopiques et représentations Galoisiennes. PhD thesis, Université Paris XI, Orsay (2002) (http://people.brandeis.edu/∼jbellaic/).Google Scholar
[4]Blasius, D. and Rogawski, J., Zeta functions of Shimura varieties, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55, part 2 (American Mathematical Society, Providence, RI, 1994), 525–571.Google Scholar
[5]Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives, in The Grothendieck Festschrift, vol. I, Progress in Mathematics, vol. 86 (Birkhäuser, Boston, MA, 1990), 333–400.Google Scholar
[6]Breuil, C. and Messing, W., Torsion étale and crystalline cohomologies, in Cohomologies p-adiques et applications arithmétiques, II, Astérisque, vol. 279 (Société Mathématique de France, Paris, 2002), 81–124.Google Scholar
[7]Cartier, P., Representations of p-adic groups: a survey, in Automorphic forms, representations and L-functions, Proceedings of Symposia in Pure Mathematics, vol. 33, part 1 (American Mathematical Society, Providence, RI, 1979), 111–155.CrossRefGoogle Scholar
[8]Casselman, W., A new nonunitarity argument for p-adic representations, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1982), 907–928.Google Scholar
[9]Chai, C.-L. and Norman, P., Bad reduction of the Siegel moduli scheme of genus two with Γ0(p)-level structure, Amer. J. Math. 112 (1990), 1003–1071.CrossRefGoogle Scholar
[10]Clozel, L., On Ribet’s level-raising theorem for U(3), Amer. J. Math. 122 (2000), 1265–1287.CrossRefGoogle Scholar
[11]de Jong, J., The moduli spaces of principally polarized abelian varieties with Γ0(p)-level structure, J. Algebraic Geom. 2 (1993), 667–688.Google Scholar
[12]Deligne, P., Formes modulaires et représentations ℓ-adiques, in Séminaire Bourbaki 1968/69, Lecture Notes in Mathematics, vol. 79 (Springer, Berlin, 1971), 347–363.Google Scholar
[13]Deligne, P. and Serre, J.-P., Formes modulaires de poids 1, Ann. Sci. Ecole Norm. Sup. (4) 7 (1974), 507–530.CrossRefGoogle Scholar
[14]Fontaine, J.-M. and Laffaille, G., Construction de représentations p-adiques, Ann. Sci. Ecole Norm. Sup. (4) 15 (1982), 547–608.CrossRefGoogle Scholar
[15]Gan, W. T., The Saito-Kurokawa space of PGSp4 and its transfer to inner forms, in Proceedings of the AIM workshop “Eisenstein Series and Applications” (Palo Alto, 2005), Progress in Mathematics, vol. 258 (Birkhäuser, Boston, MA, 2008), (http://www.math.ucsd.edu/∼wgan/.)Google Scholar
[16]Gan, W. T. and Gurevich, N., Non-tempered Arthur packets of G 2, in Automorphic representations, L-functions and applications: progress and prospects, Ohio State Univ. Math. Res. Inst. Publ., vol. 11 (de Gruyter, Berlin, 2005), 129–155.CrossRefGoogle Scholar
[17]Genestier, A. and Tilouine, J., Systemes de Taylor-Wiles pour GSp4, in Formes automorphes. II: Le cas du groupe GSp(4), Astérisque, no. 302 (Société Mathématique de France, Paris, 2005), 177–290.Google Scholar
[18]Greenberg, M., Schemata over local rings. II, Ann. of Math. (2) 78 (1963), 256–266.CrossRefGoogle Scholar
[19]Haines, T. and Ngô, B. C., Nearby cycles for local models of some Shimura varieties, Compositio Math. 133 (2002), 117–150.CrossRefGoogle Scholar
[20]Hales, T., Shalika germs on GSp(4), in Orbites unipotentes et representations. II, Astérisque, no. 171–172 (Société Mathématique de France, Paris, 1989), 195–256.Google Scholar
[21]Hales, T., The fundamental lemma for Sp(4), Proc. Amer. Math. Soc. 125 (1997), 301–308.CrossRefGoogle Scholar
[22]Jordan, B. and Livne, R., Conjecture “epsilon” for weight k>2, Bull. Amer. Math. Soc. 21 (1989), 51–56.CrossRefGoogle Scholar
[23]Kato, K., p-adic Hodge theory and values of zeta functions of modular forms, in Cohomologies p-adiques et applications arithmetiques. III, Asterisque, no. 295 (Société Mathématique de France, Paris, 2004), 117–290.Google Scholar
[24]Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras, Invent. Math. 87 (1987), 153–215.CrossRefGoogle Scholar
[25]Kottwitz, R., Sign changes in harmonic analysis on reductive groups, Trans. Amer. Math. Soc. 278 (1983), 289–297.CrossRefGoogle Scholar
[26]Kottwitz, R., Base change for unit elements of Hecke algebras, Compositio Math. 60 (1986), 237–250.Google Scholar
[27]Kudla, S., On the local theta-correspondence, Invent. Math. 83 (1986), 229–255.CrossRefGoogle Scholar
[28]Kudla, S., Notes on the local theta-correspondence, unpublished notes (http://www.math.utoronto.ca/∼skudla/ssk.research.html).Google Scholar
[29]Kudla, S., Rallis, S. and Soudry, D., On the degree 5 L-function for Sp(2), Invent. Math. 107 (1992), 483–541.CrossRefGoogle Scholar
[30]Labesse, J.-P. and Muller, W., Weak Weyl’s law for congruence subgroups, Asian J. Math. 8 (2004), 733–745.CrossRefGoogle Scholar
[31]Langlands, R., On the functional equations satisfied by Eisenstein series, Lecture Notes in Mathematics, vol. 544 (Springer, Berlin, New York, 1976).CrossRefGoogle Scholar
[32]Langlands, R. and Shelstad, D., Descent for transfer factors. The Grothendieck Festschrift, vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 485–563.Google Scholar
[33]Laumon, G., Sur la cohomologie a supports compacts des varietes de Shimura pour GSp(4)ℚ, Compositio Math. 105 (1997), 267–359.CrossRefGoogle Scholar
[34]Lazarus, X., Module universel non ramifie pour un groupe reductif p-adique. PhD thesis, Université Paris XI, Orsay (2000).Google Scholar
[35]Li, J.-S., Theta lifting for unitary representations with nonzero cohomology, Duke Math. J. 61 (1990), 913–937.CrossRefGoogle Scholar
[36]Piatetski-Shapiro, I., On the Saito–Kurokawa lifting, Invent. Math. 71 (1983), 309–338.CrossRefGoogle Scholar
[37]Ramakrishnan, D., Irreducibility and cuspidality, in Representation theory and automorphic forms, Progress in Mathematics, vol. 255 (Birkhäuser, Boston, MA, 2008), 1–27.Google Scholar
[38]Rapoport, M., On the bad reduction of Shimura varieties, in Automorphic forms, Shimura varieties, and L-functions (Ann Arbor, MI, 1988), vol. II, Perspectives in Mathematics, vol. 11 (Academic Press, Boston, MA, 1990), 253–321.Google Scholar
[39]Ribet, K., On ℓ-adic representations attached to modular forms. II, Glasgow Math. J. 27 (1985), 185–194.CrossRefGoogle Scholar
[40]Roberts, B., The theta correspondence for similitudes, Israel J. Math. 94 (1996), 285–317.CrossRefGoogle Scholar
[41]Roberts, B., The non-Archimedean theta correspondence for GSp(2) and GO(4), Trans. Amer. Math. Soc. 351 (1999), 781–811.CrossRefGoogle Scholar
[42]Rubin, K., Euler systems (Hermann Weyl lectures, The Institute for Advanced Study), Annals of Mathematics Studies, vol. 147 (Princeton University Press, Princeton, NJ, 2000).Google Scholar
[43]Sally, P. and Tadic, M., Induced representations and classifications for GSp(2,F) and Sp(2,F), Mem. Soc. Math. France 52 (1993), 75–133.Google Scholar
[44]Schmidt, R., Iwahori-spherical representations of GSp(4) and Siegel modular forms of degree 2 with square-free level, J. Math. Soc. Japan 57 (2005), 259–293.CrossRefGoogle Scholar
[45]Shelstad, D., Characters and inner forms of a quasi-split group over ℝ, Compositio Math. 39 (1979), 11–45.Google Scholar
[46]Shelstad, D., L-indistinguishability for real groups, Math. Ann. 259 (1982), 385–430.CrossRefGoogle Scholar
[47]Skinner, C. and Urban, E., Sur les déformations p-adiques de certaines représentations automorphes, J. Inst. Math. Jussieu 5 (2006), 629–698.CrossRefGoogle Scholar
[48]Sorensen, C., A generalization of level-raising congruences for algebraic modular forms, Ann. Inst. Fourier (Grenoble) 56 (2006), 1735–1766.CrossRefGoogle Scholar
[49]Soudry, D., The CAP representations of GSp(4,𝔸), J. Reine Angew. Math. 383 (1988), 87–108.Google Scholar
[50]Tate, J., Number theoretic background, in Automorphic forms, representations and L-functions (Corvallis, OR, 1977), Proceedings of Symposia in Pure Mathematics, vol. 33, part 2 (American Mathematical Society, Providence, RI, 1979), 3–26.CrossRefGoogle Scholar
[51]Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.CrossRefGoogle Scholar
[52]Tits, J., Reductive groups over local fields, in Automorphic forms, representations and L-functions, Proceedings of Symposia in Pure Mathematics, vol. 33, part 1 (American Mathematical Society, Providence, RI, 1979), 29–69.CrossRefGoogle Scholar
[53]Vigneras, M.-F., Representations ℓ-modulaires d’un groupe reductif p-adique avec ℓ≠p, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, MA, 1996).Google Scholar
[54]Waldspurger, J.-L., Le lemme fondamental implique le transfert, Compositio Math. 105 (1997), 153–236.CrossRefGoogle Scholar
[55]Weissauer, R., Four dimensional Galois representations, in Formes automorphes. II: Le cas du groupe GSp(4), Astérisque, no. 302 (Société Mathématique de France, Paris, 2005), 67–150.Google Scholar
[56]Weissauer, R., Character identities and Galois representations related to the group GSp(4), Preprint (http://www.mathi.uni-heidelberg.de/∼weissaue/papers.html).Google Scholar
[57]Weissauer, R., Endoscopy for GSp(4), Preprint (http://www.mathi.uni-heidelberg.de/∼weissaue/papers.html).Google Scholar