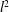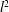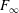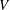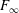Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thumann, Werner
2016.
L2–invisibility of symmetric operad groups.
Algebraic & Geometric Topology,
Vol. 16,
Issue. 4,
p.
2229.