1. Introduction
In their seminal work [Reference Kudla and RapoportKR11] and [Reference Kudla and RapoportKR14b], Kudla and Rapoport made a conjectural local arithmetic Siegel–Weil formula (the Kudla–Rapoport conjecture) relating the intersection numbers of special divisors on unitary Rapoport–Zink (RZ) spaces to the central derivative of certain local density polynomials. A unitary RZ space is a local version of a unitary Shimura variety associated to a general unitary group ![]() $\mathrm {GU}(1,n-1)$. The Kudla–Rapoport conjecture plays a central role in the arithmetic Siegel–Weil formula for unitary Shimura varieties, which was first proposed by Kudla in [Reference KudlaKud97] for orthogonal Shimura varieties. When
$\mathrm {GU}(1,n-1)$. The Kudla–Rapoport conjecture plays a central role in the arithmetic Siegel–Weil formula for unitary Shimura varieties, which was first proposed by Kudla in [Reference KudlaKud97] for orthogonal Shimura varieties. When ![]() $n=1$ or
$n=1$ or ![]() $2$, the Kudla–Rapoport conjecture was proved in [Reference Kudla and RapoportKR11]. The case when
$2$, the Kudla–Rapoport conjecture was proved in [Reference Kudla and RapoportKR11]. The case when ![]() $n=3$ was proved in [Reference TerstiegeTer13]. The general case was proved recently in [Reference Li and ZhangLZ22a] by an ingenious induction. The Archimedean analogue of the Kudla–Rapoport conjecture was proved in [Reference LiuLiu11] and [Reference Garcia and SankaranGS19]. The analogue of the Kudla–Rapoport conjecture for GSpin RZ space is formulated and proved in [Reference Li and ZhangLZ22b].
$n=3$ was proved in [Reference TerstiegeTer13]. The general case was proved recently in [Reference Li and ZhangLZ22a] by an ingenious induction. The Archimedean analogue of the Kudla–Rapoport conjecture was proved in [Reference LiuLiu11] and [Reference Garcia and SankaranGS19]. The analogue of the Kudla–Rapoport conjecture for GSpin RZ space is formulated and proved in [Reference Li and ZhangLZ22b].
Originally the Kudla–Rapoport conjecture was proposed only for good primes, namely inert primes over which the RZ space has hyperspecial level structure. A modified Kudla–Rapoport conjecture for RZ space with minuscule parahoric level structure over inert primes has been proposed in [Reference ChoCho22]. For ramified primes, there are two kinds of well-understood arithmetic models of RZ spaces. One is the exotic smooth model which has good reduction, the other is the Krämer model proposed in [Reference KrämerKrä03] which only has semi-stable reduction. The analogue of the Kudla–Rapoport conjecture for the even-dimensional exotic smooth model was studied in [Reference Li and LiuLL22], in which case the conjecture can be proved by the same strategy as in [Reference Li and ZhangLZ22a]. For the Krämer model, however, it was expected that serious modification of the original Kudla–Rapoport conjecture is needed. A precise formulation has not previously been given. One of the main goals of this paper is to formulate a precise conjecture (Conjecture 1.1) based on earlier work of [Reference ShiShi22] and [Reference He, Shi and YangHSY23] for the case ![]() $n=2$. We then prove Conjecture 1.1 for
$n=2$. We then prove Conjecture 1.1 for ![]() $n = 3$.
$n = 3$.
In a very recent joint work with Chao Li [Reference He, Li, Shi and YangHLSY22], we proved the conjecture completely. One of the major innovations of [Reference He, Li, Shi and YangHLSY22] is a decomposition formula of primitive local density polynomials, which is inspired by the results in the appendix of this work. The geometric side of the ‘horizontal’ part in [Reference He, Li, Shi and YangHLSY22] essentially follows from the current work. To deal with the vertical part in general, [Reference He, Li, Shi and YangHLSY22] uses partial Fourier transform inspired by [Reference Li and ZhangLZ22b]. The current work uses explicit computation instead. Finally, it was discovered in [Reference He, Li, Shi and YangHLSY22] that the ‘central’ derivative of the primitive local density polynomials has a surprisingly simple formula.
1.1 The naive conjecture
Let ![]() $p$ be an odd prime and
$p$ be an odd prime and ![]() $F$ be a ramified quadratic field extension of a
$F$ be a ramified quadratic field extension of a ![]() $p$-adic number field
$p$-adic number field ![]() $F_0$ with residue field
$F_0$ with residue field ![]() $\mathbb {F}_q$. Fix an algebraic closure
$\mathbb {F}_q$. Fix an algebraic closure ![]() $k$ of
$k$ of ![]() $\mathbb {F}_q$. Fix a uniformizer
$\mathbb {F}_q$. Fix a uniformizer ![]() $\pi$ of
$\pi$ of ![]() $F$ such that
$F$ such that ![]() $\pi _0=\pi ^2$ is a uniformizer of
$\pi _0=\pi ^2$ is a uniformizer of ![]() $F_0$ and let
$F_0$ and let ![]() $\mathrm {v}_\pi$ be the valuation on
$\mathrm {v}_\pi$ be the valuation on ![]() $F$ such that
$F$ such that ![]() $\mathrm {v}_\pi (\pi )=1$. Let
$\mathrm {v}_\pi (\pi )=1$. Let ![]() $\breve {F}_0$ be the completion of a maximal unramified extension of
$\breve {F}_0$ be the completion of a maximal unramified extension of ![]() $F_0$ and
$F_0$ and ![]() $\breve {F} := F\otimes _{F_0} \breve {F}_0$. Let
$\breve {F} := F\otimes _{F_0} \breve {F}_0$. Let ![]() $\mathcal {O}_{\breve F}$ and
$\mathcal {O}_{\breve F}$ and ![]() $\mathcal {O}_{\breve {F}_0}$ be the rings of integers of
$\mathcal {O}_{\breve {F}_0}$ be the rings of integers of ![]() $\breve {F}$ and
$\breve {F}$ and ![]() $\breve {F}_0$, respectively. For a Hermitian lattice or space
$\breve {F}_0$, respectively. For a Hermitian lattice or space ![]() $M$ of rank
$M$ of rank ![]() $n$, we define its sign as
$n$, we define its sign as
where ![]() $\chi$ is the quadratic character of
$\chi$ is the quadratic character of ![]() $F_0^\times$ associated to
$F_0^\times$ associated to ![]() $F/F_0$. We call
$F/F_0$. We call ![]() $M$ split or non-split depending on whether
$M$ split or non-split depending on whether ![]() $\chi (M)=1$ or
$\chi (M)=1$ or ![]() $-1$. For a Hermitian matrix
$-1$. For a Hermitian matrix ![]() $T$, define
$T$, define ![]() $\chi (T)$ to be the sign of its associated Hermitian lattice.
$\chi (T)$ to be the sign of its associated Hermitian lattice.
Let ![]() $\mathbb {Y}$ and
$\mathbb {Y}$ and ![]() $\mathbb {X}$ be pre-fixed framing Hermitian formal
$\mathbb {X}$ be pre-fixed framing Hermitian formal ![]() $\mathcal {O}_F$-modules of signature
$\mathcal {O}_F$-modules of signature ![]() $(0,1)$ and
$(0,1)$ and ![]() ${(1,n-1)}$, respectively, over
${(1,n-1)}$, respectively, over ![]() $\mathrm {Spec}\, k$. Recall that Hermitian formal
$\mathrm {Spec}\, k$. Recall that Hermitian formal ![]() $\mathcal {O}_F$-modules are a particular kind of formal
$\mathcal {O}_F$-modules are a particular kind of formal ![]() $p$-divisible groups with
$p$-divisible groups with ![]() $\mathcal {O}_F$-action, see § 2.1. The space of special quasi-homomorphisms
$\mathcal {O}_F$-action, see § 2.1. The space of special quasi-homomorphisms
is equipped with a Hermitian form ![]() $h(\,{,}\,)$, see (2.2). Let
$h(\,{,}\,)$, see (2.2). Let ![]() $\epsilon =\chi (\mathbb {V})$. The RZ space
$\epsilon =\chi (\mathbb {V})$. The RZ space ![]() $\mathcal {N}^\mathrm {Kra}_{n,\epsilon }$ parameterizes certain classes of supersingular Hermitian formal
$\mathcal {N}^\mathrm {Kra}_{n,\epsilon }$ parameterizes certain classes of supersingular Hermitian formal ![]() $\mathcal {O}_F$-modules of signature
$\mathcal {O}_F$-modules of signature ![]() $(1,n-1)$ over
$(1,n-1)$ over ![]() ${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$, see § 2.1. It is a formal scheme over
${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$, see § 2.1. It is a formal scheme over ![]() ${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ with semi-stable reduction and can be viewed as a regular model of the formal completion of the corresponding global unitary Shimura variety along its basic locus over
${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ with semi-stable reduction and can be viewed as a regular model of the formal completion of the corresponding global unitary Shimura variety along its basic locus over ![]() $p$. When
$p$. When ![]() $n$ is odd,
$n$ is odd, ![]() $\mathcal {N}^\mathrm {Kra}_{n,1}$ is isomorphic to
$\mathcal {N}^\mathrm {Kra}_{n,1}$ is isomorphic to ![]() $\mathcal {N}^\mathrm {Kra}_{n,-1}$. We often write
$\mathcal {N}^\mathrm {Kra}_{n,-1}$. We often write ![]() $\mathcal {N}^\mathrm {Kra}$ instead of
$\mathcal {N}^\mathrm {Kra}$ instead of ![]() $\mathcal {N}^\mathrm {Kra}_{n,\epsilon }$ for simplicity.
$\mathcal {N}^\mathrm {Kra}_{n,\epsilon }$ for simplicity.
For each subset ![]() $L \subset \mathbb {V}$, define
$L \subset \mathbb {V}$, define ![]() $\mathcal {Z}^\mathrm {Kra}(L)$ to be the formal subscheme of
$\mathcal {Z}^\mathrm {Kra}(L)$ to be the formal subscheme of ![]() $\mathcal {N}^\mathrm {Kra}$ where
$\mathcal {N}^\mathrm {Kra}$ where ![]() ${\bf x}$ deforms to a homomorphism for any
${\bf x}$ deforms to a homomorphism for any ![]() ${\bf x}\in L$. Let
${\bf x}\in L$. Let ![]() $L\subset \mathbb {V}$ be an
$L\subset \mathbb {V}$ be an ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $r$. We say
$r$. We say ![]() $L$ is integral if
$L$ is integral if ![]() $h(\,{,}\,)|_L$ is non-degenerate and takes values in
$h(\,{,}\,)|_L$ is non-degenerate and takes values in ![]() $\mathcal {O}_F$. Let
$\mathcal {O}_F$. Let ![]() ${\bf x}_1,\ldots,{\bf x}_r$ be a basis of
${\bf x}_1,\ldots,{\bf x}_r$ be a basis of ![]() $L$. We define
$L$. We define
where ![]() $\otimes ^\mathbb {L}$ is the derived tensor product of complex of coherent sheaves on
$\otimes ^\mathbb {L}$ is the derived tensor product of complex of coherent sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$ and
$\mathcal {N}^\mathrm {Kra}$ and ![]() $K_0(\mathcal {N}^\mathrm {Kra})$ is the Grothendieck groups of finite complexes of coherent locally free sheaves on
$K_0(\mathcal {N}^\mathrm {Kra})$ is the Grothendieck groups of finite complexes of coherent locally free sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$. By [Reference HowardHow19, Corollary C],
$\mathcal {N}^\mathrm {Kra}$. By [Reference HowardHow19, Corollary C], ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L)$ is independent of the choice of basis of
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L)$ is independent of the choice of basis of ![]() $L$. When
$L$. When ![]() $L$ has rank
$L$ has rank ![]() $n$, we define the intersection number
$n$, we define the intersection number
where ![]() $\chi$ is the Euler characteristic. One can show that
$\chi$ is the Euler characteristic. One can show that ![]() $\mathrm {Int}(L)$ is finite, see Lemma 2.14.
$\mathrm {Int}(L)$ is finite, see Lemma 2.14.
Let ![]() $L$ and
$L$ and ![]() $M$ be Hermitian lattices of rank
$M$ be Hermitian lattices of rank ![]() $n$ and
$n$ and ![]() $m$ respectively. Moreover, we assume
$m$ respectively. Moreover, we assume ![]() $\mathrm {v}(M):= \min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in M\} \ge -1.$ We use
$\mathrm {v}(M):= \min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in M\} \ge -1.$ We use ![]() $\mathrm {Herm}_{L,M}$ to denote the scheme of Hermitian
$\mathrm {Herm}_{L,M}$ to denote the scheme of Hermitian ![]() $\mathcal {O}_F$-module homomorphisms from
$\mathcal {O}_F$-module homomorphisms from ![]() $L$ to
$L$ to ![]() $M$, which is a scheme of finite type over
$M$, which is a scheme of finite type over ![]() $\mathcal {O}_{F_0}$. More specifically, for an
$\mathcal {O}_{F_0}$. More specifically, for an ![]() $\mathcal {O}_{F_0}$-algebra
$\mathcal {O}_{F_0}$-algebra ![]() $R$, we define
$R$, we define
Then
To simplify the notation, let ![]() $I(M,L,d)$ denote
$I(M,L,d)$ denote ![]() $\mathrm {Herm}_{L, M}(\mathcal {O}_{F_0}/(\pi _0^d))$. Then direct calculation shows that
$\mathrm {Herm}_{L, M}(\mathcal {O}_{F_0}/(\pi _0^d))$. Then direct calculation shows that
becomes constant for sufficiently large integers ![]() $d >0$. We call it the local density (of
$d >0$. We call it the local density (of ![]() $M$ representing
$M$ representing ![]() $L$).
$L$).
Let ![]() $\mathcal {H}$ be the (Hermitian) hyperbolic plane with Gram matrix
$\mathcal {H}$ be the (Hermitian) hyperbolic plane with Gram matrix ![]() $\mathcal {H}=\bigl (\begin {smallmatrix} 0 & \pi ^{-1}\\ -\pi ^{-1} & 0 \end {smallmatrix}\bigr )$. One can show that there is a (local density) polynomial
$\mathcal {H}=\bigl (\begin {smallmatrix} 0 & \pi ^{-1}\\ -\pi ^{-1} & 0 \end {smallmatrix}\bigr )$. One can show that there is a (local density) polynomial ![]() $\alpha (M,L,X)\in \mathbb {Q}[X]$ such that
$\alpha (M,L,X)\in \mathbb {Q}[X]$ such that
Define its derivative by
As ![]() $\alpha (M,L, X)$ (respectively,
$\alpha (M,L, X)$ (respectively, ![]() $\alpha '(M,L)$) only depends on their Gram matrices
$\alpha '(M,L)$) only depends on their Gram matrices ![]() $S$ and
$S$ and ![]() $T$, we will also denote it by
$T$, we will also denote it by ![]() $\alpha (S, T, X)$ (respectively,
$\alpha (S, T, X)$ (respectively, ![]() $\alpha '(S,T)$). Let
$\alpha '(S,T)$). Let ![]() $M$ be the unique unimodular Hermitian
$M$ be the unique unimodular Hermitian ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $n$ with
$n$ with ![]() $\chi (M)=-\chi (L)$. The naive analogue of the local Kudla–Rapoport conjecture is
$\chi (M)=-\chi (L)$. The naive analogue of the local Kudla–Rapoport conjecture is
However, this conjectural formula is not even true for ![]() $n=2$ according to the main theorem of [Reference He, Shi and YangHSY23]. The analytic side of the conjecture needs to be modified.
$n=2$ according to the main theorem of [Reference He, Shi and YangHSY23]. The analytic side of the conjecture needs to be modified.
1.2 The precise conjecture
By [Reference ShiShi18, Theorem 1.2], ![]() $\mathcal {Z}^\mathrm {Kra}(L)$ is empty when
$\mathcal {Z}^\mathrm {Kra}(L)$ is empty when ![]() $L$ is not integral, so we have
$L$ is not integral, so we have
On the analytic side, the right-hand side of (1.6) is automatically zero only when ![]() $\mathrm {v}(L) \leq -2$, and is sometimes non-zero when
$\mathrm {v}(L) \leq -2$, and is sometimes non-zero when ![]() $\mathrm {v}(L) =-1$. Thus, there should be correction terms involving Hermitian lattices
$\mathrm {v}(L) =-1$. Thus, there should be correction terms involving Hermitian lattices ![]() $M$ with
$M$ with ![]() $\mathrm {v}(M) =-1$. By [Reference JacobowitzJac62], there are
$\mathrm {v}(M) =-1$. By [Reference JacobowitzJac62], there are ![]() $n-1$ equivalent classes of Hermitian lattices which are direct sum of copies of
$n-1$ equivalent classes of Hermitian lattices which are direct sum of copies of ![]() $\mathcal {H}$ and unimodular lattices:
$\mathcal {H}$ and unimodular lattices:
where we use ![]() $I_{n-2i}^{\epsilon }$ to denote the unimodular Hermitian lattice of rank
$I_{n-2i}^{\epsilon }$ to denote the unimodular Hermitian lattice of rank ![]() $n-2i$ with
$n-2i$ with ![]() $\chi (I_{n-2i}^{\epsilon })= \chi (\mathcal {H}_{n,i}^{\epsilon } )=\epsilon$. When
$\chi (I_{n-2i}^{\epsilon })= \chi (\mathcal {H}_{n,i}^{\epsilon } )=\epsilon$. When ![]() $n=2r$ is even, we take
$n=2r$ is even, we take ![]() $I_{0, \epsilon } =0$ and
$I_{0, \epsilon } =0$ and ![]() $\mathcal {H}_{n, r}^1 = \mathcal {H}^{r}$. Then the local arithmetic Siegel–Weil formula (also known as the Kudla–Rapoport conjecture at a ramified prime) should be of the following form:
$\mathcal {H}_{n, r}^1 = \mathcal {H}^{r}$. Then the local arithmetic Siegel–Weil formula (also known as the Kudla–Rapoport conjecture at a ramified prime) should be of the following form:
 \begin{equation} \mathrm{Int}(L) = 2 \frac{\alpha'(I_{n}^{-\epsilon}, L)}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon}, L)}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})}, \end{equation}
\begin{equation} \mathrm{Int}(L) = 2 \frac{\alpha'(I_{n}^{-\epsilon}, L)}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon}, L)}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})}, \end{equation}
where ![]() $\epsilon =\chi ( L)$. Since
$\epsilon =\chi ( L)$. Since ![]() $\mathrm {Int}(\mathcal {H}_{n, j}^{\epsilon })=0$, we should have
$\mathrm {Int}(\mathcal {H}_{n, j}^{\epsilon })=0$, we should have
 \begin{equation} 2 \frac{\alpha'(I_{n}^{-\epsilon},\mathcal{H}_{n, j}^{\epsilon} )}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon},\mathcal{H}_{n,j}^{\epsilon})}{\alpha( I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} =0. \end{equation}
\begin{equation} 2 \frac{\alpha'(I_{n}^{-\epsilon},\mathcal{H}_{n, j}^{\epsilon} )}{\alpha(I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon},\mathcal{H}_{n,j}^{\epsilon})}{\alpha( I_{n}^{-\epsilon}, I_{n}^{-\epsilon})} =0. \end{equation}
This system of equations turns out to determine the coefficients ![]() $c_{n,i}^\epsilon$ uniquely by Theorem 6.1. We propose the following Kudla–Rapoport conjecture at a ramified prime.
$c_{n,i}^\epsilon$ uniquely by Theorem 6.1. We propose the following Kudla–Rapoport conjecture at a ramified prime.
Conjecture 1.1 The identity (1.8) always holds with the coefficients ![]() $c_{n,i}^\epsilon$ uniquely determined by (1.9).
$c_{n,i}^\epsilon$ uniquely determined by (1.9).
For convenience, we set
 \begin{equation} \partial \mathrm{Den}(L) =2 \frac{\alpha'(I_{n}^{-\epsilon}, L)}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon} )} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon}, L)}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon})}. \end{equation}
\begin{equation} \partial \mathrm{Den}(L) =2 \frac{\alpha'(I_{n}^{-\epsilon}, L)}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon} )} + \sum_{ i} c_{n,i}^\epsilon \frac{\alpha(\mathcal{H}_{n,i}^{\epsilon}, L)}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon})}. \end{equation}
We remark that because ![]() $\mathrm {Int}(L)$ is always an integer, Conjecture 1.1 suggests that
$\mathrm {Int}(L)$ is always an integer, Conjecture 1.1 suggests that ![]() $\partial \mathrm {Den}(L)$ should be an integer, which is already not obvious.
$\partial \mathrm {Den}(L)$ should be an integer, which is already not obvious.
The conjecture holds for ![]() $\mathcal {N}^\mathrm {Kra}_{2,\pm 1}$ by results in [Reference ShiShi22] and [Reference He, Shi and YangHSY23]. In this paper, we prove the conjecture for
$\mathcal {N}^\mathrm {Kra}_{2,\pm 1}$ by results in [Reference ShiShi22] and [Reference He, Shi and YangHSY23]. In this paper, we prove the conjecture for ![]() $n=3$ and provide some partial results in the general case.
$n=3$ and provide some partial results in the general case.
Theorem 1.2 Conjecture 1.1 is true when ![]() $n=3$.
$n=3$.
1.3 Special difference cycles
One of the novelties of this paper is the concept of special difference cycles. Let ![]() $L_1$ be an
$L_1$ be an ![]() $\mathcal {O}_F$-lattice of
$\mathcal {O}_F$-lattice of ![]() $\mathbb {V}$ of rank
$\mathbb {V}$ of rank ![]() $n_1 \le n$. Define the special difference cycle
$n_1 \le n$. Define the special difference cycle ![]() $\mathcal {D}(L_1)\in K_0 (\mathcal {N}^\mathrm {Kra})$ by
$\mathcal {D}(L_1)\in K_0 (\mathcal {N}^\mathrm {Kra})$ by
 \begin{equation} \mathcal{D}(L_1)={}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L_1)+\sum_{i=1}^{n_1} (-1)^i q^{i(i-1)/2} \sum_{\substack{L_1 \subset L'\subset \frac{1}{\pi} L_1\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L_1)=i}} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L')\in K_0(\mathcal{N}^\mathrm{Kra}). \end{equation}
\begin{equation} \mathcal{D}(L_1)={}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L_1)+\sum_{i=1}^{n_1} (-1)^i q^{i(i-1)/2} \sum_{\substack{L_1 \subset L'\subset \frac{1}{\pi} L_1\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L_1)=i}} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L')\in K_0(\mathcal{N}^\mathrm{Kra}). \end{equation}
Here ![]() $\mathcal {D}(L_1)$ can be seen as a higher codimensional analogue of the difference divisor first introduced in [Reference TerstiegeTer13, Definition 2.10]. By the definition and a
$\mathcal {D}(L_1)$ can be seen as a higher codimensional analogue of the difference divisor first introduced in [Reference TerstiegeTer13, Definition 2.10]. By the definition and a ![]() $q$-adic linear-algebraic inclusion–exclusion principle, we have (see Lemma 2.16)
$q$-adic linear-algebraic inclusion–exclusion principle, we have (see Lemma 2.16)
 \begin{equation} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L_1) =\sum_{\substack{L'\, \mathrm{integral}\\ L_1 \subset L' \subset L_{1,F}}} \mathcal{D}(L'). \end{equation}
\begin{equation} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L_1) =\sum_{\substack{L'\, \mathrm{integral}\\ L_1 \subset L' \subset L_{1,F}}} \mathcal{D}(L'). \end{equation}
Here ![]() $L_F =L\otimes _{\mathcal {O}_F} F$ for an
$L_F =L\otimes _{\mathcal {O}_F} F$ for an ![]() $\mathcal {O}_F$-lattice
$\mathcal {O}_F$-lattice ![]() $L$. The above summation is, in fact, finite. Assume that we have a decomposition
$L$. The above summation is, in fact, finite. Assume that we have a decomposition ![]() $L=L_1\oplus L_2$ of
$L=L_1\oplus L_2$ of ![]() $\mathcal {O}_F$-lattices such that
$\mathcal {O}_F$-lattices such that ![]() $L_i$ has rank
$L_i$ has rank ![]() $n_i$ and
$n_i$ and ![]() $n_1+n_2=n$. Define
$n_1+n_2=n$. Define
where ![]() $\cdot$ is the product on
$\cdot$ is the product on ![]() $K_0(\mathcal {N}^\mathrm {Kra})$ induced by tensor product of complexes. Note that this definition, in fact, depends on the decomposition of
$K_0(\mathcal {N}^\mathrm {Kra})$ induced by tensor product of complexes. Note that this definition, in fact, depends on the decomposition of ![]() $L$.
$L$.
On analytic side, we define
 \begin{equation} \partial \mathrm{Den}(L)^{(n_1)}:= \partial \mathrm{Den}(L)-\sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2} \sum_{\substack{L_1 \subset L_1' \subset L_{1, F} \\ \dim {L_1'/L_1}=i}} \partial \mathrm{Den}(L'_1\oplus L_2). \end{equation}
\begin{equation} \partial \mathrm{Den}(L)^{(n_1)}:= \partial \mathrm{Den}(L)-\sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2} \sum_{\substack{L_1 \subset L_1' \subset L_{1, F} \\ \dim {L_1'/L_1}=i}} \partial \mathrm{Den}(L'_1\oplus L_2). \end{equation}
This definition again depends on the decomposition of ![]() $L$. What motivates the definition of
$L$. What motivates the definition of ![]() $\partial \mathrm {Den}(L)^{(n_1)}$ and
$\partial \mathrm {Den}(L)^{(n_1)}$ and ![]() $\mathcal {D}(L_1)$ is the fact that
$\mathcal {D}(L_1)$ is the fact that ![]() $\partial \mathrm {Den}(L)^{(n_1)}$ is equal to the derivative of certain primitive local density polynomials, see [Reference KatsuradaKat99, Proposition 2.1] or Theorem 5.2 below. The analogue of (1.12) holds for
$\partial \mathrm {Den}(L)^{(n_1)}$ is equal to the derivative of certain primitive local density polynomials, see [Reference KatsuradaKat99, Proposition 2.1] or Theorem 5.2 below. The analogue of (1.12) holds for ![]() $\partial \mathrm {Den}(L)^{(n_1)}$. As a consequence, we have the following theorem (see Theorem 5.6 for a refinement).
$\partial \mathrm {Den}(L)^{(n_1)}$. As a consequence, we have the following theorem (see Theorem 5.6 for a refinement).
Theorem 1.3 Conjecture 1.1 is true if and only if for every lattice ![]() $L=L_1\oplus L_2$ such that
$L=L_1\oplus L_2$ such that ![]() $L_i$ has rank
$L_i$ has rank ![]() $n_i$, we have
$n_i$, we have
We speculate that ![]() $\mathcal {D}(L_1)$ is of a simple form when
$\mathcal {D}(L_1)$ is of a simple form when ![]() $n_1=n-1$. One strong piece of evidence for this is that the ‘horizontal’ part of
$n_1=n-1$. One strong piece of evidence for this is that the ‘horizontal’ part of ![]() $\mathcal {D}(L_1)$ is either empty or isomorphic to one or two copies of
$\mathcal {D}(L_1)$ is either empty or isomorphic to one or two copies of ![]() $\mathrm {Spf}\, W_s$ where
$\mathrm {Spf}\, W_s$ where ![]() $W_s$ is the integer ring of an extension of
$W_s$ is the integer ring of an extension of ![]() $\breve {F}$ of degree
$\breve {F}$ of degree ![]() $q^s$, see Proposition 4.6. Another evidence is that the intersection of
$q^s$, see Proposition 4.6. Another evidence is that the intersection of ![]() $\mathcal {D}(L_1)$ with an exceptional divisor in
$\mathcal {D}(L_1)$ with an exceptional divisor in ![]() $\mathcal {N}^\mathrm {Kra}$ is
$\mathcal {N}^\mathrm {Kra}$ is ![]() $\pm 1$ or
$\pm 1$ or ![]() $0$, see Lemma 3.9. When
$0$, see Lemma 3.9. When ![]() $n=3$, we show that
$n=3$, we show that ![]() $\mathcal {D}(L_1)$ has a simple decomposition, see Theorem 1.4.
$\mathcal {D}(L_1)$ has a simple decomposition, see Theorem 1.4.
1.4 The case  $n=3$
$n=3$
The proof of Theorem 1.2 is divided into three cases, see § 11. For ![]() $\mathrm {v}(L)<0$, we show directly
$\mathrm {v}(L)<0$, we show directly ![]() $\partial \mathrm {Den}(L)=\mathrm {Int}(L)=0$. The case
$\partial \mathrm {Den}(L)=\mathrm {Int}(L)=0$. The case ![]() $\mathrm {v}(L)=0$ is reduced to the case
$\mathrm {v}(L)=0$ is reduced to the case ![]() $n=2$, which was proved in [Reference ShiShi22] and [Reference He, Shi and YangHSY23]. For
$n=2$, which was proved in [Reference ShiShi22] and [Reference He, Shi and YangHSY23]. For ![]() $\mathrm {v}(L) >0$, we prove that
$\mathrm {v}(L) >0$, we prove that ![]() $\mathrm {Int}(L)^{(2)} = \partial \mathrm {Den}(L)^{(2)}$ for a decomposition
$\mathrm {Int}(L)^{(2)} = \partial \mathrm {Den}(L)^{(2)}$ for a decomposition ![]() $L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$, and then apply Theorem 1.3 (more precisely Theorem 5.6).
$L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$, and then apply Theorem 1.3 (more precisely Theorem 5.6).
In order to prove ![]() $\mathrm {Int}(L)^{(2)} = \partial \mathrm {Den}(L)^{(2)}$, we need to understand the decomposition of
$\mathrm {Int}(L)^{(2)} = \partial \mathrm {Den}(L)^{(2)}$, we need to understand the decomposition of ![]() $\mathcal {D}(L^\flat )$. We say a lattice
$\mathcal {D}(L^\flat )$. We say a lattice ![]() $\Lambda \subset \mathbb {V}$ is a vertex lattice if
$\Lambda \subset \mathbb {V}$ is a vertex lattice if ![]() $\pi \Lambda \subseteq \Lambda ^\sharp \subseteq \Lambda$ where
$\pi \Lambda \subseteq \Lambda ^\sharp \subseteq \Lambda$ where ![]() $\Lambda ^\sharp$ is dual lattice of
$\Lambda ^\sharp$ is dual lattice of ![]() $\Lambda$ with respect to
$\Lambda$ with respect to ![]() $h(\,{,}\,)$ and we call
$h(\,{,}\,)$ and we call ![]() $t=\mathrm {dim}_{\mathbb {F}_q}(\Lambda /\Lambda ^\sharp )$ the type of
$t=\mathrm {dim}_{\mathbb {F}_q}(\Lambda /\Lambda ^\sharp )$ the type of ![]() $\Lambda$. This has to be an even integer between
$\Lambda$. This has to be an even integer between ![]() $0$ and
$0$ and ![]() $n$. We denote the set of vertex lattices of type
$n$. We denote the set of vertex lattices of type ![]() $t$ by
$t$ by ![]() $\mathcal {V}^t$. When
$\mathcal {V}^t$. When ![]() $n=3$, a type
$n=3$, a type ![]() $2$ lattice
$2$ lattice ![]() $\Lambda _2$ corresponds to a line
$\Lambda _2$ corresponds to a line ![]() $\tilde {\mathcal {N}}_{\Lambda _2}\cong \mathbb {P}^1_k$ in
$\tilde {\mathcal {N}}_{\Lambda _2}\cong \mathbb {P}^1_k$ in ![]() $\mathcal {N}^\mathrm {Kra}_3$ and a type
$\mathcal {N}^\mathrm {Kra}_3$ and a type ![]() $0$ lattice
$0$ lattice ![]() $\Lambda _0$ corresponds to a divisor
$\Lambda _0$ corresponds to a divisor ![]() $\mathrm {Exc}_{\Lambda _0}\cong \mathbb {P}^2_k$. Let
$\mathrm {Exc}_{\Lambda _0}\cong \mathbb {P}^2_k$. Let ![]() $H_{\Lambda _0}$ be the hyperplane class of
$H_{\Lambda _0}$ be the hyperplane class of ![]() $\mathrm {Exc}_{\Lambda _0}$. We have the following theorem.
$\mathrm {Exc}_{\Lambda _0}$. We have the following theorem.
Theorem 1.4 If ![]() $\mathrm {v}(L^\flat )>0$, we have the following decomposition of cycles in
$\mathrm {v}(L^\flat )>0$, we have the following decomposition of cycles in ![]() $\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra}_3)$
$\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra}_3)$
 \[ \mathcal{D}(L^\flat)=\sum_{\substack{
\Lambda_2\in \mathcal{V}^2 \\ L^\flat \subset
\Lambda_2^\sharp}}
\biggl(2[\mathcal{O}_{\tilde{\mathcal{N}}_{\Lambda_2}}]+\sum_{\substack{\Lambda_0\in\mathcal{V}^0\\\Lambda_0\subset
\Lambda_2}}H_{\Lambda_0}\biggr), \]
\[ \mathcal{D}(L^\flat)=\sum_{\substack{
\Lambda_2\in \mathcal{V}^2 \\ L^\flat \subset
\Lambda_2^\sharp}}
\biggl(2[\mathcal{O}_{\tilde{\mathcal{N}}_{\Lambda_2}}]+\sum_{\substack{\Lambda_0\in\mathcal{V}^0\\\Lambda_0\subset
\Lambda_2}}H_{\Lambda_0}\biggr), \]
where ![]() $\mathrm {Gr}^\bullet K_0(\mathcal {N}^\mathrm {Kra}_3)$ is the associated graded ring of
$\mathrm {Gr}^\bullet K_0(\mathcal {N}^\mathrm {Kra}_3)$ is the associated graded ring of ![]() $K_0(\mathcal {N}^\mathrm {Kra}_3)$ with respect to the codimension filtration.
$K_0(\mathcal {N}^\mathrm {Kra}_3)$ with respect to the codimension filtration.
Theorem 1.4 is proved by intersecting ![]() $\mathcal {D}(L^\flat )$ with special divisors that are isomorphic to
$\mathcal {D}(L^\flat )$ with special divisors that are isomorphic to ![]() $\mathcal {N}^\mathrm {Kra}_{2,-1}$ and computing the intersection numbers in two different ways. One way relates the intersection numbers to the main result of [Reference ShiShi22]. The other way uses the decomposition in Theorem 1.4 and detects the multiplicity of each component that shows up on the right-hand side.
$\mathcal {N}^\mathrm {Kra}_{2,-1}$ and computing the intersection numbers in two different ways. One way relates the intersection numbers to the main result of [Reference ShiShi22]. The other way uses the decomposition in Theorem 1.4 and detects the multiplicity of each component that shows up on the right-hand side.
1.5 Global application
In the last part of the paper, we apply the local results above to the global intersection problem proposed by [Reference Kudla and RapoportKR14b]. For brevity and clarity of exposition we restrict our attention to the case when ![]() $F$ is an imaginary quadratic field. We remark here that our results can be applied to the case when
$F$ is an imaginary quadratic field. We remark here that our results can be applied to the case when ![]() $F$ is a general CM field given correct local assumptions. Let
$F$ is a general CM field given correct local assumptions. Let ![]() $\mathcal {M}^\mathrm {Kra}_{(1,n-1)}$ be the moduli functor over
$\mathcal {M}^\mathrm {Kra}_{(1,n-1)}$ be the moduli functor over ![]() $\mathrm {Spec}\, \mathcal {O}_F$ which parametrizes principally polarized abelian varieties
$\mathrm {Spec}\, \mathcal {O}_F$ which parametrizes principally polarized abelian varieties ![]() $A$ with an action
$A$ with an action ![]() $\iota :\mathcal {O}_F \rightarrow \mathrm {End}(A)$, a compatible polarization
$\iota :\mathcal {O}_F \rightarrow \mathrm {End}(A)$, a compatible polarization ![]() $\lambda : A\rightarrow A^\vee$ and a filtration
$\lambda : A\rightarrow A^\vee$ and a filtration ![]() $\mathcal {F}_A\subset \mathrm {Lie}\, A$ which satisfies the signature
$\mathcal {F}_A\subset \mathrm {Lie}\, A$ which satisfies the signature ![]() $(1,n-1)$ condition (see § 12.1). Let
$(1,n-1)$ condition (see § 12.1). Let ![]() $V$ be a Hermitian vector space over
$V$ be a Hermitian vector space over ![]() $F$ of signature
$F$ of signature ![]() $(n-1,1)$ containing a self-dual lattice
$(n-1,1)$ containing a self-dual lattice ![]() $L$. The lattice
$L$. The lattice ![]() $L$ determines an open and closed substack
$L$ determines an open and closed substack
which is an integral model of a unitary Shimura variety. For a point in ![]() $\mathcal {M}(S)$ (
$\mathcal {M}(S)$ (![]() $S$ an
$S$ an ![]() $\mathcal {O}_F$-scheme), i.e. a pair
$\mathcal {O}_F$-scheme), i.e. a pair ![]() $(E,\iota _0,\lambda _0)\in \mathcal {M}_{(0,1)}(S)$,
$(E,\iota _0,\lambda _0)\in \mathcal {M}_{(0,1)}(S)$, ![]() $(A,\iota,\lambda,\mathcal {F}_A)\in \mathcal {M}^\mathrm {Kra}_{(1,n-1)}(S)$, define the locally free
$(A,\iota,\lambda,\mathcal {F}_A)\in \mathcal {M}^\mathrm {Kra}_{(1,n-1)}(S)$, define the locally free ![]() $\mathcal {O}_F$-module
$\mathcal {O}_F$-module
It is equipped with the Hermitian form ![]() $h'(x,y)=\iota _0^{-1}(\lambda _0^{-1}\circ y^\vee \circ \lambda \circ x)$. For a
$h'(x,y)=\iota _0^{-1}(\lambda _0^{-1}\circ y^\vee \circ \lambda \circ x)$. For a ![]() $m \times m$ non-singular Hermitian matrix
$m \times m$ non-singular Hermitian matrix ![]() $T$ with values in
$T$ with values in ![]() $\mathcal {O}_F$, let
$\mathcal {O}_F$, let ![]() $\mathcal {Z}(T)$ be the stack of collections
$\mathcal {Z}(T)$ be the stack of collections ![]() $(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A,{\bf x})$ such that
$(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A,{\bf x})$ such that ![]() $(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A)\in \mathcal {M}(S)$,
$(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A)\in \mathcal {M}(S)$, ![]() ${\bf x} \in V'(E,A)^m$ with
${\bf x} \in V'(E,A)^m$ with ![]() $h'({\bf x},{\bf x})=T$. Then
$h'({\bf x},{\bf x})=T$. Then ![]() $\mathcal {Z}(T)$ is representable by a Deligne–Mumford stack which is finite and unramified over
$\mathcal {Z}(T)$ is representable by a Deligne–Mumford stack which is finite and unramified over ![]() $\mathcal {M}$ (see [Reference Kudla and RapoportKR14b, Proposition 2.9]). When
$\mathcal {M}$ (see [Reference Kudla and RapoportKR14b, Proposition 2.9]). When ![]() $t\in \mathbb {Z}_{>0}$, each component of
$t\in \mathbb {Z}_{>0}$, each component of ![]() $\mathcal {Z}(t)$ can be viewed as a divisor by [Reference HowardHow15, Proposition 3.2.3]. In general,
$\mathcal {Z}(t)$ can be viewed as a divisor by [Reference HowardHow15, Proposition 3.2.3]. In general, ![]() $\mathcal {Z}(T)$ does not necessarily have the expected codimension which is the rank of
$\mathcal {Z}(T)$ does not necessarily have the expected codimension which is the rank of ![]() $T$.
$T$.
Let ![]() $\mathcal {C} =\{ \mathcal {C}_p\}$ be an incoherent collection of local Hermitian spaces of rank
$\mathcal {C} =\{ \mathcal {C}_p\}$ be an incoherent collection of local Hermitian spaces of rank ![]() $n$ associated to
$n$ associated to ![]() $V$ such that
$V$ such that ![]() $\mathcal {C}_\ell \cong V_\ell$ for all finite
$\mathcal {C}_\ell \cong V_\ell$ for all finite ![]() $\ell$ and
$\ell$ and ![]() $\mathcal {C}_\infty$ is positive definite. It is ‘incoherent’ in the sense that it does not come from a global Hermitian space. For a non-singular Hermitian matrix
$\mathcal {C}_\infty$ is positive definite. It is ‘incoherent’ in the sense that it does not come from a global Hermitian space. For a non-singular Hermitian matrix ![]() $T$ of rank
$T$ of rank ![]() $n$ with values in
$n$ with values in ![]() $\mathcal {O}_F$, let
$\mathcal {O}_F$, let ![]() $V_T$ be the Hermitian space with Gram matrix
$V_T$ be the Hermitian space with Gram matrix ![]() $T$. Define
$T$. Define
Then ![]() $\mathcal {Z}(T)$ is empty if
$\mathcal {Z}(T)$ is empty if ![]() $|\mathrm {Diff}(T,\mathcal {C})|>1$. If
$|\mathrm {Diff}(T,\mathcal {C})|>1$. If ![]() $\mathrm {Diff}(T,\mathcal {C})=\{p\}$ for a finite prime
$\mathrm {Diff}(T,\mathcal {C})=\{p\}$ for a finite prime ![]() $p$ inert or ramified in
$p$ inert or ramified in ![]() $F$, then the support of
$F$, then the support of ![]() $\mathcal {Z}(T)$ is on the supersingular locus of
$\mathcal {Z}(T)$ is on the supersingular locus of ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathrm {Spec}\, \mathbb {F}_p$. Let
$\mathrm {Spec}\, \mathbb {F}_p$. Let ![]() $e$ be the ramification index of
$e$ be the ramification index of ![]() $F_p/\mathbb {Q}_p$. Define the arithmetic degree
$F_p/\mathbb {Q}_p$. Define the arithmetic degree
where ![]() $\otimes ^\mathbb {L}$ stands for derived tensor product on the category of coherent sheaves on
$\otimes ^\mathbb {L}$ stands for derived tensor product on the category of coherent sheaves on ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $\chi$ is the Euler characteristic and
$\chi$ is the Euler characteristic and ![]() $t_i$ (
$t_i$ (![]() $1 \le i \le n$) are the diagonal entries of
$1 \le i \le n$) are the diagonal entries of ![]() $T$. When
$T$. When ![]() $\mathrm {Diff}(T,\mathcal {C})=\{\infty \}$, then
$\mathrm {Diff}(T,\mathcal {C})=\{\infty \}$, then ![]() $\mathcal {Z}(T)$ is, in fact, empty and one can use integration of a green current to define the arithmetic degree
$\mathcal {Z}(T)$ is, in fact, empty and one can use integration of a green current to define the arithmetic degree ![]() $\widehat {\mathrm {deg}}_{T}(v)$ with the parameter
$\widehat {\mathrm {deg}}_{T}(v)$ with the parameter ![]() $v$ being a positive-definite Hermitian matrix
$v$ being a positive-definite Hermitian matrix ![]() $v$ of order
$v$ of order ![]() $n$ (which will be the imaginary part of
$n$ (which will be the imaginary part of ![]() $\tau$); see, for example, [Reference Li and ZhangLZ22a, § 15.3].
$\tau$); see, for example, [Reference Li and ZhangLZ22a, § 15.3].
On the analytic side, we consider an incoherent Eisenstein series ![]() $E(\tau,s,\Phi )$ for a non-standard section
$E(\tau,s,\Phi )$ for a non-standard section ![]() $\Phi$ in a degenerate principal series representation of
$\Phi$ in a degenerate principal series representation of ![]() $\mathrm {U}(n,n)(\mathbb {A})$, see § 12.2. Here
$\mathrm {U}(n,n)(\mathbb {A})$, see § 12.2. Here ![]() $\tau$ is in the Hermitian Siegel upper half space
$\tau$ is in the Hermitian Siegel upper half space
where ![]() $\mathrm {Herm}_n$ (respectively,
$\mathrm {Herm}_n$ (respectively, ![]() $\mathrm {Herm}_{n,>0}$) is the set of
$\mathrm {Herm}_{n,>0}$) is the set of ![]() $n\times n$ (positive-definite) Hermitian matrices with values in
$n\times n$ (positive-definite) Hermitian matrices with values in ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $s\in \mathbb {C}$. Our local conjecture and result imply the following theorem, which extends [Reference Li and ZhangLZ22a, Theorem 1.3.1] to include ramified primes.
$s\in \mathbb {C}$. Our local conjecture and result imply the following theorem, which extends [Reference Li and ZhangLZ22a, Theorem 1.3.1] to include ramified primes.
Theorem 1.5 (Arithmetic Siegel–Weil formula for non-singular coefficients)
Assume that the fundamental discriminant of ![]() $F$ is
$F$ is ![]() $d_F \equiv 1 \pmod 8$ and that Conjecture 1.1 holds for every
$d_F \equiv 1 \pmod 8$ and that Conjecture 1.1 holds for every ![]() $F_p$ with
$F_p$ with ![]() $p|d_F$. For any non-singular Hermitian matrix
$p|d_F$. For any non-singular Hermitian matrix ![]() $T$ with values in
$T$ with values in ![]() $\mathcal {O}_F$ of size
$\mathcal {O}_F$ of size ![]() $n$, we have
$n$, we have
where ![]() $E'_T(\tau, 0,\Phi )$ is the
$E'_T(\tau, 0,\Phi )$ is the ![]() $T$th Fourier coefficient of
$T$th Fourier coefficient of ![]() $E'(\tau, 0,\Phi )$ and
$E'(\tau, 0,\Phi )$ and ![]() $C$ is a constant that only depends on
$C$ is a constant that only depends on ![]() $F$ and
$F$ and ![]() $L$. In particular, the arithmetic Siegel–Weil formula holds for
$L$. In particular, the arithmetic Siegel–Weil formula holds for ![]() $n=2, 3$ for non-singular
$n=2, 3$ for non-singular ![]() $T$.
$T$.
In a very recent joint work with Chao Li [Reference He, Li, Shi and YangHLSY22], we proved Conjecture 1.1, and so this theorem is now unconditional.
1.6 Notation
For ![]() $\mathcal {O}_F$-lattices (respectively,
$\mathcal {O}_F$-lattices (respectively, ![]() $\mathcal {O}_{\breve F}$-lattices)
$\mathcal {O}_{\breve F}$-lattices) ![]() $L$ and
$L$ and ![]() $L'$, we write
$L'$, we write ![]() $L \stackrel {t}{\subset } L'$ if
$L \stackrel {t}{\subset } L'$ if ![]() $L\subset L' \subset ({1}/{\pi }) L$ and
$L\subset L' \subset ({1}/{\pi }) L$ and ![]() $\dim _{\mathbb {F}_q}(L'/L)=t$ (respectively,
$\dim _{\mathbb {F}_q}(L'/L)=t$ (respectively, ![]() $\dim _k (L'/L)=t$). We say a vector
$\dim _k (L'/L)=t$). We say a vector ![]() $v\in L$ is primitive if
$v\in L$ is primitive if ![]() $({1}/{\pi })v\notin L$.
$({1}/{\pi })v\notin L$.
Throughout the paper, we always assume a Hermitian lattice is non-degenerate. For Hermitian lattices ![]() $L$ and
$L$ and ![]() $L'$, we use
$L'$, we use ![]() $L{\unicode{x29BA}} L'$ to denote orthogonal direct sum, and
$L{\unicode{x29BA}} L'$ to denote orthogonal direct sum, and ![]() $L \oplus L'$ as direct sum of lattices. Given a Hermitian lattice
$L \oplus L'$ as direct sum of lattices. Given a Hermitian lattice ![]() $L$ with Hermitian form
$L$ with Hermitian form ![]() $(\, ,\, )$, we consider two different dual lattices of
$(\, ,\, )$, we consider two different dual lattices of ![]() $L$. We use
$L$. We use ![]() $L^{\sharp }$ (respectively,
$L^{\sharp }$ (respectively, ![]() $L^{\vee })$ to denote the dual lattice of
$L^{\vee })$ to denote the dual lattice of ![]() $L$ with respect to
$L$ with respect to ![]() $(\,{,}\,)$ (respectively,
$(\,{,}\,)$ (respectively, ![]() $\mathrm {tr}_{F/F_0}(\,{,}\,))$. Recall that
$\mathrm {tr}_{F/F_0}(\,{,}\,))$. Recall that ![]() $\mathrm {v}(L)$ is defined to be
$\mathrm {v}(L)$ is defined to be ![]() $\min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in L\}$. For each Hermitian lattice
$\min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in L\}$. For each Hermitian lattice ![]() $L$, there exists a Jordan decomposition
$L$, there exists a Jordan decomposition ![]() $L={\unicode{x29BA}} _{i\ge s} L_i$ such that
$L={\unicode{x29BA}} _{i\ge s} L_i$ such that ![]() $L_i^{\sharp }=\pi ^{-i} L_i$. We call
$L_i^{\sharp }=\pi ^{-i} L_i$. We call ![]() $L$ integral if
$L$ integral if ![]() $s\ge 0$. For an integral lattice
$s\ge 0$. For an integral lattice ![]() $L$, we define
$L$, we define
Following [Reference Li and LiuLL22, Definition 2.11], for a lattice ![]() $L$ with Hermitian form
$L$ with Hermitian form ![]() $(\, ,\, )$, we may find a basis of
$(\, ,\, )$, we may find a basis of ![]() $L$ whose Gram matrix is
$L$ whose Gram matrix is
for some ![]() $\beta _{1}, \ldots, \beta _{s} \in \mathcal {O}_{F_0}^{\times }$ and
$\beta _{1}, \ldots, \beta _{s} \in \mathcal {O}_{F_0}^{\times }$ and ![]() $b_{1}, \ldots, b_{s}, c_{1}, \ldots, c_{t} \in \mathbb {Z}$. Moreover, we define its (unitary) fundamental invariants
$b_{1}, \ldots, b_{s}, c_{1}, \ldots, c_{t} \in \mathbb {Z}$. Moreover, we define its (unitary) fundamental invariants ![]() $(a_1,\ldots,a_n)$ to be the unique non-decreasing rearrangement of
$(a_1,\ldots,a_n)$ to be the unique non-decreasing rearrangement of ![]() $(2 b_1,\ldots,2b_s,2c_1+1,\ldots,2c_t+1)$. The partial order of
$(2 b_1,\ldots,2b_s,2c_1+1,\ldots,2c_t+1)$. The partial order of ![]() $\mathbb {Z}^n$ induces a partial order on the set of fundamental invariants.
$\mathbb {Z}^n$ induces a partial order on the set of fundamental invariants.
Let ![]() $\mathcal {H}_i=\bigl (\!\begin {smallmatrix}0 & \pi ^{i}\\ (-\pi )^{i} & 0 \end {smallmatrix}\!\bigr )$ and
$\mathcal {H}_i=\bigl (\!\begin {smallmatrix}0 & \pi ^{i}\\ (-\pi )^{i} & 0 \end {smallmatrix}\!\bigr )$ and ![]() $\mathcal {H}=\mathcal {H}_{-1}$. We also use it to denote a Hermitian lattice with Gram matrix
$\mathcal {H}=\mathcal {H}_{-1}$. We also use it to denote a Hermitian lattice with Gram matrix ![]() $\mathcal {H}_i$. Given a Hermitian lattice
$\mathcal {H}_i$. Given a Hermitian lattice ![]() $M$, we use
$M$, we use ![]() $M^{[k]}$ to denote
$M^{[k]}$ to denote ![]() $M{\unicode{x29BA}} \mathcal {H}^k$. We use
$M{\unicode{x29BA}} \mathcal {H}^k$. We use ![]() $I_m^\epsilon$ to denote a unimodular Hermitian lattice of rank
$I_m^\epsilon$ to denote a unimodular Hermitian lattice of rank ![]() $m$ and
$m$ and ![]() $\chi (I_m^\epsilon )=\epsilon$. For a Hermitian matrix
$\chi (I_m^\epsilon )=\epsilon$. For a Hermitian matrix ![]() $T$, we define
$T$, we define ![]() $\mathrm {v}(T)=\mathrm {v}(L)$ where
$\mathrm {v}(T)=\mathrm {v}(L)$ where ![]() $L$ is a lattice whose Gram matrix is
$L$ is a lattice whose Gram matrix is ![]() $T$. We use
$T$. We use ![]() $\mathrm {Herm}_n(F)$ to denote the set of Hermitian matrices over
$\mathrm {Herm}_n(F)$ to denote the set of Hermitian matrices over ![]() $F$ of size
$F$ of size ![]() $n$. When there is no confusion, we also simply denote it as
$n$. When there is no confusion, we also simply denote it as ![]() $\mathrm {Herm}_n$. For
$\mathrm {Herm}_n$. For ![]() $T,T'\in \mathrm {Herm}_n(F)$, we say
$T,T'\in \mathrm {Herm}_n(F)$, we say ![]() $T$ is equivalent to
$T$ is equivalent to ![]() $T'$ if there is a
$T'$ if there is a ![]() $U\in \mathrm {GL}_n(\mathcal {O}_F)$ such that
$U\in \mathrm {GL}_n(\mathcal {O}_F)$ such that ![]() $U^*TU=T'$, where
$U^*TU=T'$, where ![]() $U^*= {}^t \bar U$. In this case, we denote it as
$U^*= {}^t \bar U$. In this case, we denote it as ![]() $T\approx T'$.
$T\approx T'$.
For ![]() $t\in \mathcal {O}_{F_0}$, let
$t\in \mathcal {O}_{F_0}$, let ![]() $\mathrm {v}(t):= \mathrm {val}_{\pi _0}(t)$ and write
$\mathrm {v}(t):= \mathrm {val}_{\pi _0}(t)$ and write ![]() $t=t_0(-\pi _0)^{\mathrm {v}(t)}$. For
$t=t_0(-\pi _0)^{\mathrm {v}(t)}$. For ![]() $x\in \mathbb {V}$, we set
$x\in \mathbb {V}$, we set ![]() $q(x)=(x,x)$ and
$q(x)=(x,x)$ and ![]() $\mathrm {v}(x)=\mathrm {v}(q(x))$. We use
$\mathrm {v}(x)=\mathrm {v}(q(x))$. We use ![]() $\langle t \rangle$ to denote a lattice
$\langle t \rangle$ to denote a lattice ![]() $\mathcal {O}_F x$ of rank one with
$\mathcal {O}_F x$ of rank one with ![]() $q(x)=t$.
$q(x)=t$.
The notation in each section that is not mentioned here will be explained at the very beginning of the section.
1.7 The structure of the paper
The paper is divided into three parts. In Part 1, we prove some facts about special cycles for arbitrary ![]() $n$. More specifically, in § 2 we recall some basic facts about
$n$. More specifically, in § 2 we recall some basic facts about ![]() $\mathcal {N}^\mathrm {Kra}$ and define special cycles and special difference cycles on it. In § 3, we compute the intersection number between special cycles and the exceptional divisors. In § 4, we prove a decomposition theorem for the horizontal component of
$\mathcal {N}^\mathrm {Kra}$ and define special cycles and special difference cycles on it. In § 3, we compute the intersection number between special cycles and the exceptional divisors. In § 4, we prove a decomposition theorem for the horizontal component of ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ when
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ when ![]() $L^\flat$ has rank
$L^\flat$ has rank ![]() $n-1$.
$n-1$.
Part 2 is about Hermitian local densities. In § 5, we study induction formulas of local density polynomials and relate the local density polynomials with primitive local densities. In § 6, we show that the coefficients ![]() $c_{n,i}^\epsilon$ in (1.9) are uniquely determined and give an algorithm to compute them. In §§ 7 and 8, we compute the local density polynomials when
$c_{n,i}^\epsilon$ in (1.9) are uniquely determined and give an algorithm to compute them. In §§ 7 and 8, we compute the local density polynomials when ![]() $n\leq 3$.
$n\leq 3$.
In Part 3 we prove Theorem 1.2, i.e. Conjecture 1.1 for ![]() $n=3$. In § 9, we study the reduced locus of the special cycles for
$n=3$. In § 9, we study the reduced locus of the special cycles for ![]() $n=3$. In § 10, we decompose
$n=3$. In § 10, we decompose ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ for
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ for ![]() $L^\flat$ of rank
$L^\flat$ of rank ![]() $2$ and of valuation 0, and compute the intersection number of
$2$ and of valuation 0, and compute the intersection number of ![]() $\tilde {\mathcal {N}}_{\Lambda _2}$ with
$\tilde {\mathcal {N}}_{\Lambda _2}$ with ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})$. Finally, we prove Theorem 1.4, finish the proof of Theorem 1.2 in § 11, and explain its global applications in § 12.
$\mathcal {Z}^\mathrm {Kra}({\bf x})$. Finally, we prove Theorem 1.4, finish the proof of Theorem 1.2 in § 11, and explain its global applications in § 12.
In Appendix A, we compute the primitive local densities that are used in Part 2 of the paper.
Part 1. The geometric side
2. RZ space and special cycle
We denote ![]() $\bar {a}$ the Galois conjugate of
$\bar {a}$ the Galois conjugate of ![]() $a\in F$ over
$a\in F$ over ![]() $F_0$. Let
$F_0$. Let ![]() $\mathrm {Nilp}\, \mathcal {O}_{\breve F}$ be the category of
$\mathrm {Nilp}\, \mathcal {O}_{\breve F}$ be the category of ![]() $\mathcal {O}_{\breve F}$-schemes
$\mathcal {O}_{\breve F}$-schemes ![]() $S$ such that
$S$ such that ![]() $\pi$ is locally nilpotent on
$\pi$ is locally nilpotent on ![]() $S$. For such an
$S$. For such an ![]() $S$, denote its special fiber
$S$, denote its special fiber ![]() $S\times _{\mathrm {Spf}\, \mathcal {O}_{\breve F}} \mathrm {Spec}\, k$ by
$S\times _{\mathrm {Spf}\, \mathcal {O}_{\breve F}} \mathrm {Spec}\, k$ by ![]() $\bar S$. Let
$\bar S$. Let ![]() $\sigma$ be the Frobenius element of
$\sigma$ be the Frobenius element of ![]() $\breve {F}_0/F_0$.
$\breve {F}_0/F_0$.
2.1 RZ spaces
Let ![]() $S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$. A
$S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$. A ![]() $p$-divisible strict
$p$-divisible strict ![]() $\mathcal {O}_{F_0}$-module over
$\mathcal {O}_{F_0}$-module over ![]() $S$ is a
$S$ is a ![]() $p$-divisible group over
$p$-divisible group over ![]() $S$ with an
$S$ with an ![]() $\mathcal {O}_{F_0}$ action whose induced action on its Lie algebra is via the structural morphism
$\mathcal {O}_{F_0}$ action whose induced action on its Lie algebra is via the structural morphism ![]() $\mathcal {O}_{F_0}\rightarrow \mathcal {O}_S$.
$\mathcal {O}_{F_0}\rightarrow \mathcal {O}_S$.
Definition 2.1 A formal Hermitian ![]() $\mathcal {O}_F$-module of dimension
$\mathcal {O}_F$-module of dimension ![]() $n$ over
$n$ over ![]() $S$ is a triple
$S$ is a triple ![]() $(X,\iota,\lambda )$ where
$(X,\iota,\lambda )$ where ![]() $X$ is a supersingular
$X$ is a supersingular ![]() $p$-divisible strict
$p$-divisible strict ![]() $\mathcal {O}_{F_0}$-module over
$\mathcal {O}_{F_0}$-module over ![]() $S$ of dimension
$S$ of dimension ![]() $n$ and
$n$ and ![]() $F_0$-height
$F_0$-height ![]() $2n$ (supersingular means the relative Dieudonné module of
$2n$ (supersingular means the relative Dieudonné module of ![]() $X$ at each geometric point of
$X$ at each geometric point of ![]() $S$ has slope
$S$ has slope ![]() $\tfrac {1}{2}$),
$\tfrac {1}{2}$), ![]() $\iota :\mathcal {O}_F\rightarrow \mathrm {End}(X)$ is an
$\iota :\mathcal {O}_F\rightarrow \mathrm {End}(X)$ is an ![]() $\mathcal {O}_F$-action and
$\mathcal {O}_F$-action and ![]() $\lambda :X\rightarrow X^\vee$ is a principal polarization in the category of strict
$\lambda :X\rightarrow X^\vee$ is a principal polarization in the category of strict ![]() $\mathcal {O}_{F_0}$-modules such that the Rosati involution induced by
$\mathcal {O}_{F_0}$-modules such that the Rosati involution induced by ![]() $\lambda$ is the Galois conjugation of
$\lambda$ is the Galois conjugation of ![]() $F/F_0$ when restricted on
$F/F_0$ when restricted on ![]() $\mathcal {O}_F$. We say
$\mathcal {O}_F$. We say ![]() $(X,\iota,\lambda )$ satisfies the signature condition
$(X,\iota,\lambda )$ satisfies the signature condition ![]() $(1,n-1)$ if for all
$(1,n-1)$ if for all ![]() $a\in \mathcal {O}_F$ we have:
$a\in \mathcal {O}_F$ we have:
(i)
 $\mathrm {char}(\iota (a)\mid \mathrm {Lie}\, X)=(T-s(a))\cdot (T-s(\bar {a}))^{n-1}$ where
$\mathrm {char}(\iota (a)\mid \mathrm {Lie}\, X)=(T-s(a))\cdot (T-s(\bar {a}))^{n-1}$ where  $s:\mathcal {O}_F\rightarrow \mathcal {O}_S$ is the structure morphism;
$s:\mathcal {O}_F\rightarrow \mathcal {O}_S$ is the structure morphism;(ii) the wedge condition proposed in [Reference PappasPap00],
 \[ \wedge^n(\iota(a)-s(a)\mid \mathrm{Lie}\, X)=0,\quad \wedge^2(\iota(a)-s(\bar{a})\mid \mathrm{Lie}\, X)=0. \]
\[ \wedge^n(\iota(a)-s(a)\mid \mathrm{Lie}\, X)=0,\quad \wedge^2(\iota(a)-s(\bar{a})\mid \mathrm{Lie}\, X)=0. \]
Let ![]() $(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ be a formal Hermitian
$(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ be a formal Hermitian ![]() $\mathcal {O}_F$-module of dimension
$\mathcal {O}_F$-module of dimension ![]() $n$ over
$n$ over ![]() $k$, and
$k$, and ![]() $N$ be its rational relative Dieudonne module. Then
$N$ be its rational relative Dieudonne module. Then ![]() $N$ is an
$N$ is an ![]() $2n$-dimensional
$2n$-dimensional ![]() $\breve {F}_0$-vector space equipped with a
$\breve {F}_0$-vector space equipped with a ![]() $\sigma$-linear operator
$\sigma$-linear operator ![]() $\mathbf {F}$ and a
$\mathbf {F}$ and a ![]() $\sigma ^{-1}$-linear operator
$\sigma ^{-1}$-linear operator ![]() $\mathbf {V}$. The
$\mathbf {V}$. The ![]() $\mathcal {O}_F$-action
$\mathcal {O}_F$-action ![]() $\iota _\mathbb {X}:\mathcal {O}_F\rightarrow \mathrm {End}(\mathbb {X})$ induces on
$\iota _\mathbb {X}:\mathcal {O}_F\rightarrow \mathrm {End}(\mathbb {X})$ induces on ![]() $N$ an
$N$ an ![]() $\mathcal {O}_F$-action commuting with
$\mathcal {O}_F$-action commuting with ![]() $\mathbf {F}$ and
$\mathbf {F}$ and ![]() $\mathbf {V}$. We still denote this induced action by
$\mathbf {V}$. We still denote this induced action by ![]() $\iota _\mathbb {X}$ and denote
$\iota _\mathbb {X}$ and denote ![]() $\iota _\mathbb {X}(\pi )$ by
$\iota _\mathbb {X}(\pi )$ by ![]() $\pi$. Let
$\pi$. Let ![]() $\tau := \pi \mathbf {V}^{-1}$ and
$\tau := \pi \mathbf {V}^{-1}$ and ![]() $C:= N^\tau$. Then
$C:= N^\tau$. Then ![]() $C$ is an
$C$ is an ![]() $n$-dimensional
$n$-dimensional ![]() $F$-vector space equipped with a Hermitian form
$F$-vector space equipped with a Hermitian form ![]() $(\,{,}\,)_\mathbb {X}$ defined using the polarization
$(\,{,}\,)_\mathbb {X}$ defined using the polarization ![]() $\lambda _\mathbb {X}$, see [Reference ShiShi18, Equation (2.7)]. When
$\lambda _\mathbb {X}$, see [Reference ShiShi18, Equation (2.7)]. When ![]() $n$ is odd, there is a unique choice of
$n$ is odd, there is a unique choice of ![]() $(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ up to quasi-isogenies that preserves the polarization by a factor in
$(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ up to quasi-isogenies that preserves the polarization by a factor in ![]() $\mathcal {O}_{F_0}^\times$. When
$\mathcal {O}_{F_0}^\times$. When ![]() $n$ is even, there are two such choices according to the sign
$n$ is even, there are two such choices according to the sign ![]() $\epsilon =\chi (C)$ (see (1.1)) of
$\epsilon =\chi (C)$ (see (1.1)) of ![]() $C$. See [Reference ShiShi18, Remark 2.16] and [Reference Rapoport, Terstiege and WilsonRTW14, Remark 4.2]. Fix a formal Hermitian
$C$. See [Reference ShiShi18, Remark 2.16] and [Reference Rapoport, Terstiege and WilsonRTW14, Remark 4.2]. Fix a formal Hermitian ![]() $\mathcal {O}_F$-module
$\mathcal {O}_F$-module ![]() $(\mathbb {Y},\iota _\mathbb {Y},\lambda _\mathbb {Y})$ of signature
$(\mathbb {Y},\iota _\mathbb {Y},\lambda _\mathbb {Y})$ of signature ![]() $(0,1)$ over
$(0,1)$ over ![]() $\mathrm {Spec}\, k$. It is unique up to
$\mathrm {Spec}\, k$. It is unique up to ![]() $\mathcal {O}_F$-linear isomorphisms. Define
$\mathcal {O}_F$-linear isomorphisms. Define
which is equipped with a Hermitian form
where ![]() $y^\vee$ is the dual quasi-homomorphism of
$y^\vee$ is the dual quasi-homomorphism of ![]() $y$ and
$y$ and ![]() $\mathrm {End}^0_F(\mathbb {Y})$ is the ring of
$\mathrm {End}^0_F(\mathbb {Y})$ is the ring of ![]() $F$-linear quasi-endomorphisms of
$F$-linear quasi-endomorphisms of ![]() $\mathbb {Y}$. The Hermitian spaces
$\mathbb {Y}$. The Hermitian spaces ![]() $(\mathbb {V},h(\,{,}\,))$ and
$(\mathbb {V},h(\,{,}\,))$ and ![]() $(C,(, )_\mathbb {X})$ are related by the
$(C,(, )_\mathbb {X})$ are related by the ![]() $F$-linear isomorphism
$F$-linear isomorphism
where ![]() $e$ is a generator of the relative covariant Dieudonné module
$e$ is a generator of the relative covariant Dieudonné module ![]() $M(\mathbb {Y})$ of
$M(\mathbb {Y})$ of ![]() $\mathbb {Y}$. Let
$\mathbb {Y}$. Let ![]() $(\,{,}\,)_\mathbb {Y}$ be the analogue of
$(\,{,}\,)_\mathbb {Y}$ be the analogue of ![]() $(\,{,}\,)_\mathbb {X}$ for
$(\,{,}\,)_\mathbb {X}$ for ![]() $\mathbb {Y}$, namely the Hermitian form on the rational relative Dieudonné module of
$\mathbb {Y}$, namely the Hermitian form on the rational relative Dieudonné module of ![]() $\mathbb {Y}$ defined by
$\mathbb {Y}$ defined by ![]() $\lambda _\mathbb {Y}$. By [Reference ShiShi18, Lemma 3.6], we have
$\lambda _\mathbb {Y}$. By [Reference ShiShi18, Lemma 3.6], we have
By scaling the Hermitian form ![]() $(\,{,}\,)_\mathbb {Y}$ we can assume that
$(\,{,}\,)_\mathbb {Y}$ we can assume that
so ![]() $\mathbb {V}$ and
$\mathbb {V}$ and ![]() $C$ are isomorphic as Hermitian spaces. We will sometimes identify
$C$ are isomorphic as Hermitian spaces. We will sometimes identify ![]() $\mathbb {V}$ and
$\mathbb {V}$ and ![]() $C$.
$C$.
Definition 2.2 Fix a formal Hermitian ![]() $\mathcal {O}_F$-module
$\mathcal {O}_F$-module ![]() $(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ of dimension
$(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ of dimension ![]() $n$ over
$n$ over ![]() $k$ with the sign
$k$ with the sign ![]() $\epsilon =\chi (C)$. The moduli space
$\epsilon =\chi (C)$. The moduli space ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Pap}$ is the functor sending each
$\mathcal {N}_{n,\epsilon }^\mathrm {Pap}$ is the functor sending each ![]() $S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the groupoid of isomorphism classes of quadruples
$S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the groupoid of isomorphism classes of quadruples ![]() $(X,\iota,\lambda,\rho )$ where
$(X,\iota,\lambda,\rho )$ where ![]() $(X,\iota,\lambda )$ is a formal Hermitian
$(X,\iota,\lambda )$ is a formal Hermitian ![]() $\mathcal {O}_F$-module over
$\mathcal {O}_F$-module over ![]() $S$ of signature
$S$ of signature ![]() $(1,n-1)$ and
$(1,n-1)$ and ![]() $\rho :X\times _{S}\bar {S} \rightarrow \mathbb {X} \times _{\mathrm {Spec}\, k} \bar {S}$ is a quasi-morphism of formal
$\rho :X\times _{S}\bar {S} \rightarrow \mathbb {X} \times _{\mathrm {Spec}\, k} \bar {S}$ is a quasi-morphism of formal ![]() $\mathcal {O}_F$-modules of height
$\mathcal {O}_F$-modules of height ![]() $0$. An isomorphism between two such quadruples
$0$. An isomorphism between two such quadruples ![]() $(X,\iota,\lambda,\rho )$ and
$(X,\iota,\lambda,\rho )$ and ![]() $(X',\iota ',\lambda ',\rho ')$ is given by an
$(X',\iota ',\lambda ',\rho ')$ is given by an ![]() $\mathcal {O}_F$-linear isomorphism
$\mathcal {O}_F$-linear isomorphism ![]() $\alpha :X\rightarrow X'$ such that
$\alpha :X\rightarrow X'$ such that ![]() $\rho '\circ (\alpha \times _S \bar {S})=\rho$ and
$\rho '\circ (\alpha \times _S \bar {S})=\rho$ and ![]() $\alpha ^*(\lambda ')$ is a
$\alpha ^*(\lambda ')$ is a ![]() $\mathcal {O}_{F_0}^\times$ multiple of
$\mathcal {O}_{F_0}^\times$ multiple of ![]() $\lambda$. We drop the subscript
$\lambda$. We drop the subscript ![]() $\epsilon$ in
$\epsilon$ in ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Pap}$ when we do not emphasize on the sign.
$\mathcal {N}_{n,\epsilon }^\mathrm {Pap}$ when we do not emphasize on the sign.
By the discussion before (2.1), when ![]() $n$ is odd, two different choices of
$n$ is odd, two different choices of ![]() $\epsilon$ give us isomorphic moduli spaces. When
$\epsilon$ give us isomorphic moduli spaces. When ![]() $n$ is even, two different choices of
$n$ is even, two different choices of ![]() $\epsilon$ give us two sets of non-isomorphic moduli spaces. By [Reference Rapoport, Terstiege and WilsonRTW14],
$\epsilon$ give us two sets of non-isomorphic moduli spaces. By [Reference Rapoport, Terstiege and WilsonRTW14], ![]() $\mathcal {N}_n^\mathrm {Pap}$ is representable by a formal scheme flat and of relative dimension
$\mathcal {N}_n^\mathrm {Pap}$ is representable by a formal scheme flat and of relative dimension ![]() $n-1$ over
$n-1$ over ![]() $\mathrm {Spf}\, \mathcal {O}_{\breve F}$. We remark here that although [Reference Rapoport, Terstiege and WilsonRTW14] works on the category of
$\mathrm {Spf}\, \mathcal {O}_{\breve F}$. We remark here that although [Reference Rapoport, Terstiege and WilsonRTW14] works on the category of ![]() $p$-divisible groups (namely when
$p$-divisible groups (namely when ![]() $F_0=\mathbb {Q}_p$), their arguments and results easily extend to the category of strict formal
$F_0=\mathbb {Q}_p$), their arguments and results easily extend to the category of strict formal ![]() $\mathcal {O}_{F_0}$-modules using relative Dieudonné theory or more generally the relative display theory developed in [Reference Ahsendorf, Cheng and ZinkACZ16]. When
$\mathcal {O}_{F_0}$-modules using relative Dieudonné theory or more generally the relative display theory developed in [Reference Ahsendorf, Cheng and ZinkACZ16]. When ![]() $n=1$, we have
$n=1$, we have ![]() $\mathcal {N}_1^\mathrm {Pap}\cong \mathrm {Spf}\, \mathcal {O}_{\breve F}$. The universal Hermitian
$\mathcal {N}_1^\mathrm {Pap}\cong \mathrm {Spf}\, \mathcal {O}_{\breve F}$. The universal Hermitian ![]() $\mathcal {O}_F$-module over
$\mathcal {O}_F$-module over ![]() $\mathcal {N}_1^\mathrm {Pap}$ is the canonical lifting
$\mathcal {N}_1^\mathrm {Pap}$ is the canonical lifting ![]() $(\mathcal {G},\iota _\mathcal {G},\lambda _\mathcal {G},\rho _\mathcal {G})$ of
$(\mathcal {G},\iota _\mathcal {G},\lambda _\mathcal {G},\rho _\mathcal {G})$ of ![]() $(\mathbb {Y},\iota _\mathbb {Y},\lambda _\mathbb {Y})$ to
$(\mathbb {Y},\iota _\mathbb {Y},\lambda _\mathbb {Y})$ to ![]() $\mathrm {Spf}\, \mathcal {O}_{\breve F}$ in the sense of [Reference GrossGro86]. When
$\mathrm {Spf}\, \mathcal {O}_{\breve F}$ in the sense of [Reference GrossGro86]. When ![]() $n>1$,
$n>1$, ![]() $\mathcal {N}_n^\mathrm {Pap}$ is regular outside the set of superspecial points over
$\mathcal {N}_n^\mathrm {Pap}$ is regular outside the set of superspecial points over ![]() $\mathrm {Spec}\, k$, which are the points characterized by the condition
$\mathrm {Spec}\, k$, which are the points characterized by the condition ![]() $\iota (\pi )|_{\mathrm {Lie}\, X}=0$. The set of superspecial points is in fact the set of type
$\iota (\pi )|_{\mathrm {Lie}\, X}=0$. The set of superspecial points is in fact the set of type ![]() $0$ lattices (see § 2.3), hence is isolated and we denote it by Sing.
$0$ lattices (see § 2.3), hence is isolated and we denote it by Sing.
Definition 2.3 Fix ![]() $(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ be as in Definition 2.2. The moduli space
$(\mathbb {X},\iota _\mathbb {X},\lambda _\mathbb {X})$ be as in Definition 2.2. The moduli space ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ is the functor sending each
$\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ is the functor sending each ![]() $S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the groupoid of isomorphism classes of quintuples
$S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the groupoid of isomorphism classes of quintuples ![]() $(X,\iota,\lambda,\rho,\mathcal {F})$ where
$(X,\iota,\lambda,\rho,\mathcal {F})$ where ![]() $(X,\iota,\lambda,\rho )\in \mathcal {N}_{n,\epsilon }^\mathrm {Pap}(S)$ and
$(X,\iota,\lambda,\rho )\in \mathcal {N}_{n,\epsilon }^\mathrm {Pap}(S)$ and ![]() $\mathcal {F}$ is a locally free direct summand of
$\mathcal {F}$ is a locally free direct summand of ![]() $\mathrm {Lie}\, X$ of rank
$\mathrm {Lie}\, X$ of rank ![]() $n-1$ as an
$n-1$ as an ![]() $\mathcal {O}_S$-module such that
$\mathcal {O}_S$-module such that ![]() $\mathcal {O}_F$ acts on
$\mathcal {O}_F$ acts on ![]() $\mathrm {Lie}\, X/\mathcal {F}$ by the structural morphism and acts on
$\mathrm {Lie}\, X/\mathcal {F}$ by the structural morphism and acts on ![]() $\mathcal {F}$ by the Galois conjugate of the structural morphism. An isomorphism between two such quintuples
$\mathcal {F}$ by the Galois conjugate of the structural morphism. An isomorphism between two such quintuples ![]() $(X,\iota,\lambda,\rho,\mathcal {F})$ and
$(X,\iota,\lambda,\rho,\mathcal {F})$ and ![]() $(X',\iota ',\lambda ',\rho ',\mathcal {F}')$ is an isomorphism
$(X',\iota ',\lambda ',\rho ',\mathcal {F}')$ is an isomorphism ![]() $\alpha :(X,\iota,\lambda,\rho )\rightarrow (X',\iota ',\lambda ',\rho ')$ in
$\alpha :(X,\iota,\lambda,\rho )\rightarrow (X',\iota ',\lambda ',\rho ')$ in ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Pap}(S)$ such that
$\mathcal {N}_{n,\epsilon }^\mathrm {Pap}(S)$ such that ![]() $\alpha ^*(\mathcal {F}')=\mathcal {F}$. Again we drop the subscript
$\alpha ^*(\mathcal {F}')=\mathcal {F}$. Again we drop the subscript ![]() $\epsilon$ in
$\epsilon$ in ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ when we do not emphasize on the sign.
$\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ when we do not emphasize on the sign.
By [Reference KrämerKrä03] (see also [Reference ShiShi22, Proposition 2.7]), the natural forgetful functor ![]() $\Phi :\mathcal {N}_n^\mathrm {Kra}\rightarrow \mathcal {N}_n^\mathrm {Pap}$ forgetting
$\Phi :\mathcal {N}_n^\mathrm {Kra}\rightarrow \mathcal {N}_n^\mathrm {Pap}$ forgetting ![]() $\mathcal {F}$ is the blow up of
$\mathcal {F}$ is the blow up of ![]() $\mathcal {N}_n^\mathrm {Pap}$ along its singular locus Sing. For each point
$\mathcal {N}_n^\mathrm {Pap}$ along its singular locus Sing. For each point ![]() $\Lambda \in \mathrm {Sing}$, its inverse image
$\Lambda \in \mathrm {Sing}$, its inverse image ![]() $\Phi ^{-1}(\Lambda )$ is an exceptional divisor
$\Phi ^{-1}(\Lambda )$ is an exceptional divisor ![]() $\mathrm {Exc}_\Lambda$ isomorphic to
$\mathrm {Exc}_\Lambda$ isomorphic to ![]() $\mathbb {P}^{n-1}_k$.
$\mathbb {P}^{n-1}_k$.
2.2 Special cycles
Definition 2.4 For an ![]() $\mathcal {O}_F$-lattice
$\mathcal {O}_F$-lattice ![]() $L$ of
$L$ of ![]() $\mathbb {V}$, define
$\mathbb {V}$, define ![]() $\mathcal {Z}^\mathrm {Pap}(L)$ to be the subfunctor of
$\mathcal {Z}^\mathrm {Pap}(L)$ to be the subfunctor of ![]() $\mathcal {N}_n^\mathrm {Pap}$ sending each
$\mathcal {N}_n^\mathrm {Pap}$ sending each ![]() $S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the isomorphism classes of tuples
$S\in \mathrm {Nilp}\, \mathcal {O}_{\breve F}$ to the isomorphism classes of tuples ![]() $(X,\iota,\lambda,\rho )\in \mathcal {N}_n^\mathrm {Pap}(S)$ such that for any
$(X,\iota,\lambda,\rho )\in \mathcal {N}_n^\mathrm {Pap}(S)$ such that for any ![]() $x\in L$ the quasi-homomorphism
$x\in L$ the quasi-homomorphism
extends to a homomorphism ![]() $\mathcal {G}_S\rightarrow X$. For
$\mathcal {G}_S\rightarrow X$. For ![]() ${\bf x}\in \mathbb {V}^m$, we let
${\bf x}\in \mathbb {V}^m$, we let ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x}):= \mathcal {Z}^\mathrm {Pap} (L)$ where
$\mathcal {Z}^\mathrm {Pap}({\bf x}):= \mathcal {Z}^\mathrm {Pap} (L)$ where ![]() $L=\mathrm {Span} \{{\bf x}\}$. Let
$L=\mathrm {Span} \{{\bf x}\}$. Let
By Grothendieck–Messing theory ![]() $\mathcal {Z}^\mathrm {Pap}(L)$ (hence,
$\mathcal {Z}^\mathrm {Pap}(L)$ (hence, ![]() $\mathcal {Z}^\mathrm {Kra}(L)$) is a closed formal subscheme of
$\mathcal {Z}^\mathrm {Kra}(L)$) is a closed formal subscheme of ![]() $\mathcal {N}_n^\mathrm {Pap}$
$\mathcal {N}_n^\mathrm {Pap}$ ![]() $(\mathcal{N}_n^{\mathrm{Kra}})$. We sometimes add the subscript
$(\mathcal{N}_n^{\mathrm{Kra}})$. We sometimes add the subscript ![]() $_{n,\epsilon }$ to
$_{n,\epsilon }$ to ![]() $\mathcal {Z}^\mathrm {Pap}(L)$,
$\mathcal {Z}^\mathrm {Pap}(L)$, ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})$,
$\mathcal {Z}^\mathrm {Pap}({\bf x})$, ![]() $\mathcal {Z}^\mathrm {Kra}(L)$ and
$\mathcal {Z}^\mathrm {Kra}(L)$ and ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})$ to indicate their ambient moduli spaces.
$\mathcal {Z}^\mathrm {Kra}({\bf x})$ to indicate their ambient moduli spaces.
Definition 2.5 For an ![]() $\mathcal {O}_F$-lattice
$\mathcal {O}_F$-lattice ![]() $L\subset \mathbb {V}$, define
$L\subset \mathbb {V}$, define ![]() $\tilde {\mathcal {Z}}(L)$ to be the strict transform (see the definition after [Reference HartshorneHar13, Chapter II and Corrollary 7.15]) of
$\tilde {\mathcal {Z}}(L)$ to be the strict transform (see the definition after [Reference HartshorneHar13, Chapter II and Corrollary 7.15]) of ![]() $\mathcal {Z}^\mathrm {Pap}(L)$ under the blow up
$\mathcal {Z}^\mathrm {Pap}(L)$ under the blow up ![]() $\mathcal {N}_n^\mathrm {Kra}\rightarrow \mathcal {N}_n^\mathrm {Pap}$.
$\mathcal {N}_n^\mathrm {Kra}\rightarrow \mathcal {N}_n^\mathrm {Pap}$.
Proposition 2.6 Suppose ![]() $\chi (\mathbb {V})=\epsilon$. Let
$\chi (\mathbb {V})=\epsilon$. Let ![]() $L$ be a self-dual lattice of rank
$L$ be a self-dual lattice of rank ![]() $m$ in
$m$ in ![]() $\mathbb {V}$ with
$\mathbb {V}$ with ![]() $\eta =\chi (L)$. We have
$\eta =\chi (L)$. We have
Proof. Let us start with the case ![]() $L=\mathrm {Span}\{{\bf x}_0\}$ where
$L=\mathrm {Span}\{{\bf x}_0\}$ where ![]() ${\bf x}_0\in \mathbb {V}$. Assume that
${\bf x}_0\in \mathbb {V}$. Assume that ![]() $u=h({\bf x}_0,{\bf x}_0)$. Multiplying the Hermitian form
$u=h({\bf x}_0,{\bf x}_0)$. Multiplying the Hermitian form ![]() $(\,{,}\,)_\mathbb {X}$ on
$(\,{,}\,)_\mathbb {X}$ on ![]() $C$ by
$C$ by ![]() $u^{-1}$ does not affect the various moduli spaces involved. Thus, we can perform this and assume that
$u^{-1}$ does not affect the various moduli spaces involved. Thus, we can perform this and assume that ![]() $h({\bf x}_0,{\bf x}_0)=1$. Moreover, the sign of its orthogonal complement in
$h({\bf x}_0,{\bf x}_0)=1$. Moreover, the sign of its orthogonal complement in ![]() $\mathbb {V}$ becomes
$\mathbb {V}$ becomes
Then for ![]() $(X,\iota,\lambda,\rho )\in \mathcal {Z}^\mathrm {Pap}_{n,\epsilon }({\bf x}_0)(S)$, we define
$(X,\iota,\lambda,\rho )\in \mathcal {Z}^\mathrm {Pap}_{n,\epsilon }({\bf x}_0)(S)$, we define
By the fact that ![]() $h({\bf x}_0,{\bf x}_0)=1$ we know that
$h({\bf x}_0,{\bf x}_0)=1$ we know that ![]() $e$ is an idempotent. It is routine to check that
$e$ is an idempotent. It is routine to check that
is an object in ![]() $\mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}(S)$. Conversely given
$\mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}(S)$. Conversely given ![]() $(Y,\iota _Y,\lambda _Y,\rho _Y)\in \mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}(S)$, the object
$(Y,\iota _Y,\lambda _Y,\rho _Y)\in \mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}(S)$, the object
is in ![]() $\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}({\bf x}_0)(S)$ where
$\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}({\bf x}_0)(S)$ where ![]() $g\in \mathrm {U}(\mathbb {V})$ such that
$g\in \mathrm {U}(\mathbb {V})$ such that ![]() $g^{-1}{\bf x}_0$ is the inclusion
$g^{-1}{\bf x}_0$ is the inclusion ![]() $0\times \mathrm {id}:\mathbb {Y} \rightarrow \mathbb {X}_{n-1} \times \mathbb {Y}$ where
$0\times \mathrm {id}:\mathbb {Y} \rightarrow \mathbb {X}_{n-1} \times \mathbb {Y}$ where ![]() $\mathbb {X}_{n-1}$ is the framing object of
$\mathbb {X}_{n-1}$ is the framing object of ![]() $\mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}$. The above two functors are inverse to each other. This shows that
$\mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}$. The above two functors are inverse to each other. This shows that ![]() $\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}({\bf x}_0)\cong \mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}$. For general
$\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}({\bf x}_0)\cong \mathcal {N}_{n-1,\epsilon _1}^\mathrm {Pap}$. For general ![]() $L$ of rank
$L$ of rank ![]() $m$ and determinant
$m$ and determinant ![]() $u$, find a basis with Gram matrix
$u$, find a basis with Gram matrix ![]() $\{1,\ldots,1,u\}$ and apply the above result repeatedly. Thus, we have
$\{1,\ldots,1,u\}$ and apply the above result repeatedly. Thus, we have ![]() $\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}(L)\cong \mathcal {N}_{n-m,\epsilon _m}^\mathrm {Pap}$ where
$\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}(L)\cong \mathcal {N}_{n-m,\epsilon _m}^\mathrm {Pap}$ where
Note that by scaling the Hermitian form by ![]() $(-1)^m u$ again we have a
$(-1)^m u$ again we have a ![]() $\mathcal {N}_{n-m,\epsilon _m}^\mathrm {Pap}=\mathcal {N}_{n-m,\epsilon \eta }^\mathrm {Pap}$. It then follows from [Reference HartshorneHar13, Chapter II and Corollary 7.15] that
$\mathcal {N}_{n-m,\epsilon _m}^\mathrm {Pap}=\mathcal {N}_{n-m,\epsilon \eta }^\mathrm {Pap}$. It then follows from [Reference HartshorneHar13, Chapter II and Corollary 7.15] that ![]() $\tilde {\mathcal {Z}}_{n,\epsilon }(L)$ is the blow up of
$\tilde {\mathcal {Z}}_{n,\epsilon }(L)$ is the blow up of ![]() $\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}(L)$ along its superspecial points, which is
$\mathcal {Z}_{n,\epsilon }^\mathrm {Pap}(L)$ along its superspecial points, which is ![]() $\mathcal {N}_{n-m,\epsilon \eta }^\mathrm {Kra}$.
$\mathcal {N}_{n-m,\epsilon \eta }^\mathrm {Kra}$.
Corollary 2.7 Let ![]() $L$ be as in Proposition 2.6 and
$L$ be as in Proposition 2.6 and ![]() $\mathbf {y}\in \mathbb {V}$ such that
$\mathbf {y}\in \mathbb {V}$ such that ![]() $\mathbf {y}\bot L$. Then
$\mathbf {y}\bot L$. Then
Remark 2.8 It follows directly from the definition that ![]() $\tilde {\mathcal {Z}}(L)$ is a closed sub-formal scheme of
$\tilde {\mathcal {Z}}(L)$ is a closed sub-formal scheme of ![]() $\tilde {\mathcal {Z}}({\bf x}_1)\cap \cdots \cap \tilde {\mathcal {Z}}({\bf x}_r)$ if
$\tilde {\mathcal {Z}}({\bf x}_1)\cap \cdots \cap \tilde {\mathcal {Z}}({\bf x}_r)$ if ![]() $\{{\bf x}_1,\ldots,{\bf x}_r\}$ is a basis of
$\{{\bf x}_1,\ldots,{\bf x}_r\}$ is a basis of ![]() $L$. However, in general, these two cannot be identified.
$L$. However, in general, these two cannot be identified.
2.3 Bruhat–Tits stratification
For an ![]() $\mathcal {O}_{\breve F}$-lattice
$\mathcal {O}_{\breve F}$-lattice ![]() $M$ of
$M$ of ![]() $N$, define
$N$, define ![]() $M^\sharp$ to be the dual lattice of
$M^\sharp$ to be the dual lattice of ![]() $M$ with respect to the form
$M$ with respect to the form ![]() $(\,{,}\,)_\mathbb {X}$. Recall the following results.
$(\,{,}\,)_\mathbb {X}$. Recall the following results.
Proposition 2.9 [Reference Rapoport, Terstiege and WilsonRTW14, Proposition 2.2 and 2.4]
Let ![]() $\mathcal {N}(k)$ be the set of
$\mathcal {N}(k)$ be the set of ![]() $\mathcal {O}_{\breve F}$-lattices
$\mathcal {O}_{\breve F}$-lattices
Then the map
is a bijection.
We say a lattice ![]() $\Lambda \subset C$ is a vertex lattice if
$\Lambda \subset C$ is a vertex lattice if ![]() $\pi \Lambda \subseteq \Lambda ^\sharp \subseteq \Lambda$ where
$\pi \Lambda \subseteq \Lambda ^\sharp \subseteq \Lambda$ where ![]() $\Lambda ^\sharp$ is dual lattice of
$\Lambda ^\sharp$ is dual lattice of ![]() $\Lambda$ with respect to
$\Lambda$ with respect to ![]() $(\,{,}\,)_\mathbb {X}$, and we call
$(\,{,}\,)_\mathbb {X}$, and we call ![]() $t=\mathrm {dim}_{\mathbb {F}_q}(\Lambda /\Lambda ^\sharp )$ the type of
$t=\mathrm {dim}_{\mathbb {F}_q}(\Lambda /\Lambda ^\sharp )$ the type of ![]() $\Lambda$. We denote the set of vertex lattices (respectively, of type
$\Lambda$. We denote the set of vertex lattices (respectively, of type ![]() $t$) by
$t$) by ![]() $\mathcal {V}$ (respectively,
$\mathcal {V}$ (respectively, ![]() $\mathcal {V}^t$). We say two vertex lattices
$\mathcal {V}^t$). We say two vertex lattices ![]() $\Lambda _1$ and
$\Lambda _1$ and ![]() $\Lambda _2$ are neighbours if
$\Lambda _2$ are neighbours if ![]() $\Lambda _1\subset \Lambda _2$ or
$\Lambda _1\subset \Lambda _2$ or ![]() $\Lambda _2\subset \Lambda _1$. Then we can define a simplicial complex
$\Lambda _2\subset \Lambda _1$. Then we can define a simplicial complex ![]() $\mathcal {L}$ as follows. When
$\mathcal {L}$ as follows. When ![]() $n$ is odd or when
$n$ is odd or when ![]() $n$ is even and
$n$ is even and ![]() $C$ is non-split, then an
$C$ is non-split, then an ![]() $r$-simplex is formed by
$r$-simplex is formed by ![]() $\Lambda _0,\ldots,\Lambda _r$ if any two members of this set are neighbours. When
$\Lambda _0,\ldots,\Lambda _r$ if any two members of this set are neighbours. When ![]() $n$ is even and
$n$ is even and ![]() $C$ is split, we refer to discussion before [Reference Rapoport, Terstiege and WilsonRTW14, 3.4] for the definition of
$C$ is split, we refer to discussion before [Reference Rapoport, Terstiege and WilsonRTW14, 3.4] for the definition of ![]() $\mathcal {L}$. We also use
$\mathcal {L}$. We also use ![]() $\mathcal {L}_{n,\epsilon }$ to denote
$\mathcal {L}_{n,\epsilon }$ to denote ![]() $\mathcal {L}$ if
$\mathcal {L}$ if ![]() $C$ has dimension
$C$ has dimension ![]() $n$ and
$n$ and ![]() $\chi (C)=\epsilon$. Again when
$\chi (C)=\epsilon$. Again when ![]() $n$ is odd,
$n$ is odd, ![]() $\mathcal {L}_{n,1}=\mathcal {L}_{n,-1}$, hence we use
$\mathcal {L}_{n,1}=\mathcal {L}_{n,-1}$, hence we use ![]() $\mathcal {L}_n$ to denote it.
$\mathcal {L}_n$ to denote it.
By results in §§ 4 and 6 of [Reference Rapoport, Terstiege and WilsonRTW14], to each ![]() $\Lambda \in \mathcal {V}^t$ we can associate Deligne–Lusztig varieties
$\Lambda \in \mathcal {V}^t$ we can associate Deligne–Lusztig varieties ![]() $\mathcal {N}_\Lambda$ and
$\mathcal {N}_\Lambda$ and ![]() $\mathcal {N}_\Lambda ^\circ$ of dimension
$\mathcal {N}_\Lambda ^\circ$ of dimension ![]() $t/2$, such that
$t/2$, such that
and
Here ![]() $\Lambda (M)$ is the minimal vertex lattice such that
$\Lambda (M)$ is the minimal vertex lattice such that ![]() $\Lambda (M)\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ contains
$\Lambda (M)\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ contains ![]() $M$ which always exists by [Reference Rapoport, Terstiege and WilsonRTW14, Proposition 4.1]. By Theorem 1.1 of [Reference Rapoport, Terstiege and WilsonRTW14], we know that
$M$ which always exists by [Reference Rapoport, Terstiege and WilsonRTW14, Proposition 4.1]. By Theorem 1.1 of [Reference Rapoport, Terstiege and WilsonRTW14], we know that
and
where each ![]() $\mathcal {N}_\Lambda$ is a closed subvariety of
$\mathcal {N}_\Lambda$ is a closed subvariety of ![]() $\mathcal {N}^\mathrm {Pap}_{\mathrm {red}}$. By [Reference Rapoport, Terstiege and WilsonRTW14], we also know that
$\mathcal {N}^\mathrm {Pap}_{\mathrm {red}}$. By [Reference Rapoport, Terstiege and WilsonRTW14], we also know that
 \[ \mathcal{N}_\Lambda\cap\mathcal{N}_{\Lambda'}=\begin{cases} \mathcal{N}_{\Lambda\cap\Lambda'}, & \text{if } \Lambda\cap\Lambda'\in \mathcal{V},\\ \emptyset, & \text{otherwise}. \end{cases} \]
\[ \mathcal{N}_\Lambda\cap\mathcal{N}_{\Lambda'}=\begin{cases} \mathcal{N}_{\Lambda\cap\Lambda'}, & \text{if } \Lambda\cap\Lambda'\in \mathcal{V},\\ \emptyset, & \text{otherwise}. \end{cases} \]
For a lattice ![]() $L\subset \mathbb {V}$, define
$L\subset \mathbb {V}$, define
When ![]() $L=\mathrm {Span} \{{\bf x}\}$ we also denote
$L=\mathrm {Span} \{{\bf x}\}$ we also denote ![]() $\mathcal {V}(L)$ (respectively,
$\mathcal {V}(L)$ (respectively, ![]() $\mathcal {V}^t(L)$) by
$\mathcal {V}^t(L)$) by ![]() $\mathcal {V}({\bf x})$ (respectively,
$\mathcal {V}({\bf x})$ (respectively, ![]() $\mathcal {V}^t({\bf x})$). For any subset
$\mathcal {V}^t({\bf x})$). For any subset ![]() $S$ of
$S$ of ![]() $\mathcal {V}$, we define
$\mathcal {V}$, we define ![]() $\mathcal {L}(S)$ to be the subcomplex of
$\mathcal {L}(S)$ to be the subcomplex of ![]() $\mathcal {L}$ such that a simplex is in
$\mathcal {L}$ such that a simplex is in ![]() $\mathcal {L}(S)$ if and only if every vertex in it is in
$\mathcal {L}(S)$ if and only if every vertex in it is in ![]() $S$. For a lattice
$S$. For a lattice ![]() $L$ of
$L$ of ![]() $\mathcal {V}$ and
$\mathcal {V}$ and ![]() ${\bf x}\in C$, define
${\bf x}\in C$, define
When ![]() $L=\mathrm {Span} \{{\bf x}\}$ we also denote
$L=\mathrm {Span} \{{\bf x}\}$ we also denote ![]() $\mathcal {L}(L)$ by
$\mathcal {L}(L)$ by ![]() $\mathcal {L}({\bf x})$.
$\mathcal {L}({\bf x})$.
2.4 Horizontal and vertical part
A formal scheme ![]() $X$ over
$X$ over ![]() $\mathrm {Spf}\, \mathcal {O}_{\breve F}$ is called horizontal (respectively, vertical) if it is flat over
$\mathrm {Spf}\, \mathcal {O}_{\breve F}$ is called horizontal (respectively, vertical) if it is flat over ![]() ${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ (respectively,
${\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ (respectively, ![]() $\pi$ is locally nilpotent on
$\pi$ is locally nilpotent on ![]() $\mathcal {O}_X$). For a formal scheme
$\mathcal {O}_X$). For a formal scheme ![]() $X$ over
$X$ over ![]() $\mathrm {Spf}\, O_{\breve F}$, its horizontal part
$\mathrm {Spf}\, O_{\breve F}$, its horizontal part ![]() $X_{h}$ is canonically defined by the ideal sheaf
$X_{h}$ is canonically defined by the ideal sheaf ![]() $\mathcal {O}_{X,\mathrm {tor}}$ of torsion sections on
$\mathcal {O}_{X,\mathrm {tor}}$ of torsion sections on ![]() $\mathcal {O}_X$. If
$\mathcal {O}_X$. If ![]() $X$ is Noetherian, there exists a
$X$ is Noetherian, there exists a ![]() $m\in \mathbb {Z}_{>0}$ such that
$m\in \mathbb {Z}_{>0}$ such that ![]() $\pi ^m \mathcal {O}_{X,\mathrm {tor}}=0$. We define the vertical part
$\pi ^m \mathcal {O}_{X,\mathrm {tor}}=0$. We define the vertical part ![]() $X_{v}\subset X$ to be the closed formal subscheme defined by the ideal sheaf
$X_{v}\subset X$ to be the closed formal subscheme defined by the ideal sheaf ![]() $\pi ^m \mathcal {O}_X$. Since
$\pi ^m \mathcal {O}_X$. Since ![]() $\mathcal {O}_{X,\mathrm {tor}}\cap \pi ^m \mathcal {O}_X=\{0\}$, we have the following decomposition by primary decomposition:
$\mathcal {O}_{X,\mathrm {tor}}\cap \pi ^m \mathcal {O}_X=\{0\}$, we have the following decomposition by primary decomposition:
as a union of horizontal and vertical formal subschemes. Note that the horizontal part ![]() $X_{h}$ is canonically defined whereas the vertical part
$X_{h}$ is canonically defined whereas the vertical part ![]() $X_{v}$ depends on the choice of
$X_{v}$ depends on the choice of ![]() $m$.
$m$.
Lemma 2.10 For a lattice ![]() $L^\flat \subset \mathbb {V}$ of rank greater or equal to
$L^\flat \subset \mathbb {V}$ of rank greater or equal to ![]() $n-1$ with non-degenerate Hermitian form,
$n-1$ with non-degenerate Hermitian form, ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is Noetherian.
$\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is Noetherian.
Proof. The lemma can be proved as in [Reference Li and ZhangLZ22a, Lemma 2.9.2].
Lemma 2.11 For a rank ![]() $n-1$ lattice
$n-1$ lattice ![]() $L^\flat \subset \mathbb {V}$ with non-degenerate Hermitian form,
$L^\flat \subset \mathbb {V}$ with non-degenerate Hermitian form, ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )_v$ is supported on the reduced locus
$\mathcal {Z}^\mathrm {Kra}(L^\flat )_v$ is supported on the reduced locus ![]() $\mathcal {N}^\mathrm {Kra}_{\mathrm {red}}$ of
$\mathcal {N}^\mathrm {Kra}_{\mathrm {red}}$ of ![]() $\mathcal {N}^\mathrm {Kra}$, i.e.
$\mathcal {N}^\mathrm {Kra}$, i.e. ![]() $\mathcal {O}_{\mathcal {Z}^\mathrm {Kra}(L^\flat )_v}$ is annihilated by a power of the ideal sheaf of
$\mathcal {O}_{\mathcal {Z}^\mathrm {Kra}(L^\flat )_v}$ is annihilated by a power of the ideal sheaf of ![]() $\mathcal {N}^\mathrm {Kra}_{\mathrm {red}}$.
$\mathcal {N}^\mathrm {Kra}_{\mathrm {red}}$.
Proof. The proof is the same as that of [Reference Li and ZhangLZ22a, Lemma 5.1.1].
2.5 Derived special cycles
For a locally Noetherian formal scheme ![]() $X$ together with a formal subscheme
$X$ together with a formal subscheme ![]() $Y$, denote by
$Y$, denote by ![]() $K_0^Y(X)$ the Grothendieck group of finite complexes of coherent locally free
$K_0^Y(X)$ the Grothendieck group of finite complexes of coherent locally free ![]() $\mathcal {O}_X$-modules acyclic outside
$\mathcal {O}_X$-modules acyclic outside ![]() $Y$. For such a complex
$Y$. For such a complex ![]() $A^\bullet$, denote by
$A^\bullet$, denote by ![]() $[A^\bullet ]$ the element in
$[A^\bullet ]$ the element in ![]() $K_0^Y(X)$ represented by it. We use
$K_0^Y(X)$ represented by it. We use ![]() $K_0(X)$ to denote
$K_0(X)$ to denote ![]() $K_0^X(X)$. Denote by
$K_0^X(X)$. Denote by ![]() $\mathrm {F}^i K_0^Y(X)$ the codimension
$\mathrm {F}^i K_0^Y(X)$ the codimension ![]() $i$ filtration on
$i$ filtration on ![]() $K_0^Y(X)$ and
$K_0^Y(X)$ and ![]() $\mathrm {Gr}^i K_0^Y(X)$ its
$\mathrm {Gr}^i K_0^Y(X)$ its ![]() $i$th graded piece. We have a cup product
$i$th graded piece. We have a cup product ![]() $\cdot$ on
$\cdot$ on ![]() $K_0^Y(X)$ defined by tensor product of complexes:
$K_0^Y(X)$ defined by tensor product of complexes:
When ![]() $X$ is a scheme, the cup product satisfies [Reference Soulé, Abramovich, Burnol and KramerSABK94, § I.3 and Theorem 1.3]
$X$ is a scheme, the cup product satisfies [Reference Soulé, Abramovich, Burnol and KramerSABK94, § I.3 and Theorem 1.3]
It is expected that (2.8) is also true when ![]() $X$ is a formal scheme. We only need special cases of this fact which can be checked directly; see, for example, Lemmas 3.4 and 10.1.
$X$ is a formal scheme. We only need special cases of this fact which can be checked directly; see, for example, Lemmas 3.4 and 10.1.
Let ![]() $K'_0(Y)$ be the Grothendieck group of coherent sheaves of
$K'_0(Y)$ be the Grothendieck group of coherent sheaves of ![]() $\mathcal {O}_Y$-modules on
$\mathcal {O}_Y$-modules on ![]() $Y$. When
$Y$. When ![]() $X$ is regular we have the following isomorphism:
$X$ is regular we have the following isomorphism:
In particular, ![]() $K_0(X)\cong K'_0(X)$.
$K_0(X)\cong K'_0(X)$.
When ![]() $X$ is a regular scheme of dimension
$X$ is a regular scheme of dimension ![]() $d$, there is an isomorphism of graded rings defined by the Chern character:
$d$, there is an isomorphism of graded rings defined by the Chern character:
 \[ \mathrm{ch}:K_0(X)_\mathbb{Q}\cong \bigoplus_{i=1}^d \mathrm{CH}^i(X)_\mathbb{Q}. \]
\[ \mathrm{ch}:K_0(X)_\mathbb{Q}\cong \bigoplus_{i=1}^d \mathrm{CH}^i(X)_\mathbb{Q}. \]
In particular, we have
Recall that for ![]() ${\bf x}\in \mathbb {V}$,
${\bf x}\in \mathbb {V}$, ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor, see [Reference HowardHow19, Proposition 4.3].
$\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor, see [Reference HowardHow19, Proposition 4.3].
Definition 2.12 For ![]() ${\bf x}=({\bf x}_1,\ldots,{\bf x}_r)\in \mathbb {V}^r$, define
${\bf x}=({\bf x}_1,\ldots,{\bf x}_r)\in \mathbb {V}^r$, define ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}({\bf x})$ to be
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}({\bf x})$ to be
where ![]() $\otimes ^\mathbb {L}$ is the derived tensor product of complexes of coherent locally free sheaves on
$\otimes ^\mathbb {L}$ is the derived tensor product of complexes of coherent locally free sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$. By [Reference HowardHow19, Theorem B],
$\mathcal {N}^\mathrm {Kra}$. By [Reference HowardHow19, Theorem B], ![]() ${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}({\bf x})$ only depends on
${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}({\bf x})$ only depends on ![]() $L:= \mathrm {Span}\{{\bf x}\}$, hence can be denoted as
$L:= \mathrm {Span}\{{\bf x}\}$, hence can be denoted as ![]() ${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)$.
${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)$.
Definition 2.13 When ![]() $L$ has rank
$L$ has rank ![]() $n$, we define the intersection number
$n$, we define the intersection number
where ![]() $\chi$ is the Euler characteristic.
$\chi$ is the Euler characteristic.
Lemma 2.14 The subscheme ![]() $\mathcal {Z}^\mathrm {Kra}(L)$ is properly supported on
$\mathcal {Z}^\mathrm {Kra}(L)$ is properly supported on ![]() $\mathcal {N}_{\mathrm {red}}^\mathrm {Kra}$. In particular,
$\mathcal {N}_{\mathrm {red}}^\mathrm {Kra}$. In particular, ![]() $\mathrm {Int}(L)$ is finite.
$\mathrm {Int}(L)$ is finite.
Proof. This can be proved exactly the same way as [Reference Li and ZhangLZ22a, Lemma 2.10.1].
2.6 Special difference cycles
Conjecture 1.1 and Theorem 5.2 motivate us to make the following definition.
Definition 2.15 For ![]() $L\subset \mathbb {V}$ a rank
$L\subset \mathbb {V}$ a rank ![]() $\ell$ lattice, define the special difference cycle
$\ell$ lattice, define the special difference cycle ![]() $\mathcal {D}(L)\in K_0^{\mathcal {Z}^\mathrm {Kra}(L)} (\mathcal {N}^\mathrm {Kra})$ by
$\mathcal {D}(L)\in K_0^{\mathcal {Z}^\mathrm {Kra}(L)} (\mathcal {N}^\mathrm {Kra})$ by
 \begin{equation} \mathcal{D}(L)={}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L)+\sum_{i=1}^\ell (-1)^i q^{i(i-1)/2} \sum_{\substack{L\subset L'\subset \frac{1}{\pi} L\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L)=i}} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L'). \end{equation}
\begin{equation} \mathcal{D}(L)={}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L)+\sum_{i=1}^\ell (-1)^i q^{i(i-1)/2} \sum_{\substack{L\subset L'\subset \frac{1}{\pi} L\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L)=i}} {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L'). \end{equation} One interesting observation is the following decomposition of ![]() ${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)$.
${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)$.
Lemma 2.16 For ![]() $L\subset \mathbb {V}$ a lattice of rank
$L\subset \mathbb {V}$ a lattice of rank ![]() $\ell$, we have the following identity in
$\ell$, we have the following identity in ![]() $K_0^{\mathcal {Z}^\mathrm {Kra}(L)} (\mathcal {N}^\mathrm {Kra})$ where the summation is finite:
$K_0^{\mathcal {Z}^\mathrm {Kra}(L)} (\mathcal {N}^\mathrm {Kra})$ where the summation is finite:
 \[ {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L) =\sum_{\substack{L'\,\mathrm{integral} \\L \subset L' \subset L_F}} \mathcal{D}(L'). \]
\[ {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L) =\sum_{\substack{L'\,\mathrm{integral} \\L \subset L' \subset L_F}} \mathcal{D}(L'). \]
Proof. First, if ![]() $L$ is not integral, neither is
$L$ is not integral, neither is ![]() $L'$ if
$L'$ if ![]() $L\subset L'$. In this case
$L\subset L'$. In this case ![]() ${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)=0$ and the summation index on the right-hand side of the identity in the lemma is empty. This proves the lemma when
${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L)=0$ and the summation index on the right-hand side of the identity in the lemma is empty. This proves the lemma when ![]() $\mathrm {v}(L)<0$. We can now prove the identity by induction on the fundamental invariant of
$\mathrm {v}(L)<0$. We can now prove the identity by induction on the fundamental invariant of ![]() $L$. Assume that the lemma is proved for all
$L$. Assume that the lemma is proved for all ![]() $L'\subset L_F$ with
$L'\subset L_F$ with ![]() $L\subsetneq L'$.
$L\subsetneq L'$.
For ![]() $L'$ with
$L'$ with ![]() $L\subsetneq L'\subset ({1}/{\pi }) L$, we have
$L\subsetneq L'\subset ({1}/{\pi }) L$, we have
by the induction hypothesis. Combining this with (2.12), we can write
where ![]() $m(L'')\in \mathbb {Z}$. Now it suffices to show
$m(L'')\in \mathbb {Z}$. Now it suffices to show ![]() $m(L'')=1$ for any
$m(L'')=1$ for any ![]() $L''$ such that
$L''$ such that ![]() $L\subset L'' \subset L_F$.
$L\subset L'' \subset L_F$.
First, note that ![]() $m(L)=1$. For any
$m(L)=1$. For any ![]() $L''$ such that
$L''$ such that ![]() $L\subset L''\subsetneq L_F$, let
$L\subset L''\subsetneq L_F$, let ![]() $M'=({1}/{\pi })L\cap L''$ and
$M'=({1}/{\pi })L\cap L''$ and ![]() $m=\dim _{\mathbb {F}_q} (M'/L)$. We have
$m=\dim _{\mathbb {F}_q} (M'/L)$. We have
 \begin{equation} m(L'')=-\sum_{i=1}^m (-1)^i q^{i(i-1)/2} \sum_{\substack{L\subset L'\subset M'\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L)=i}} 1=1 \end{equation}
\begin{equation} m(L'')=-\sum_{i=1}^m (-1)^i q^{i(i-1)/2} \sum_{\substack{L\subset L'\subset M'\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L)=i}} 1=1 \end{equation}
by evaluating the identity in the corollary to [Reference TamagawaTam63, Lemma 12] at ![]() $t=1$.
$t=1$.
Remark 2.17 When ![]() $\ell =1$ and
$\ell =1$ and ![]() $L=\mathrm {Span}\{{\bf x}\}$, the Cartier divisor
$L=\mathrm {Span}\{{\bf x}\}$, the Cartier divisor
is the difference divisor ![]() $\mathcal {D}({\bf x})$ defined in [Reference TerstiegeTer13, Definition 2.10].
$\mathcal {D}({\bf x})$ defined in [Reference TerstiegeTer13, Definition 2.10].
Definition 2.18 Assume ![]() $L=L_1\oplus L_2$, where
$L=L_1\oplus L_2$, where ![]() $L_i$ is of rank
$L_i$ is of rank ![]() $n_i$ and
$n_i$ and ![]() $n_1+n_2=n$. We define
$n_1+n_2=n$. We define
Notice that ![]() $\mathrm {Int}(L)^{(n_1)}$ depends on the decomposition
$\mathrm {Int}(L)^{(n_1)}$ depends on the decomposition ![]() $L=L_1\oplus L_2$.
$L=L_1\oplus L_2$.
3. Special cycles and exceptional divisors
For a formal subscheme ![]() $\mathcal {Z}$ of
$\mathcal {Z}$ of ![]() $\mathcal {N}^\mathrm {Kra}$, we use the notation
$\mathcal {N}^\mathrm {Kra}$, we use the notation ![]() $\otimes _{\mathcal {Z}}$ (respectively,
$\otimes _{\mathcal {Z}}$ (respectively, ![]() $\otimes _{\mathcal {Z}}^\mathbb {L}$) instead of
$\otimes _{\mathcal {Z}}^\mathbb {L}$) instead of ![]() $\otimes _{\mathcal {O}_\mathcal {Z}}$ (respectively,
$\otimes _{\mathcal {O}_\mathcal {Z}}$ (respectively, ![]() $\otimes _{\mathcal {O}_\mathcal {Z}}^\mathbb {L}$). We also simply write
$\otimes _{\mathcal {O}_\mathcal {Z}}^\mathbb {L}$). We also simply write ![]() $\otimes$ (respectively,
$\otimes$ (respectively, ![]() $\otimes ^\mathbb {L}$) instead of
$\otimes ^\mathbb {L}$) instead of ![]() $\otimes _{\mathcal {N}^\mathrm {Kra}}$ (respectively,
$\otimes _{\mathcal {N}^\mathrm {Kra}}$ (respectively, ![]() $\otimes _{\mathcal {N}^\mathrm {Kra}}^\mathbb {L}$). Let us first recall the following distribution law of derived tensor product. In this section, we identify
$\otimes _{\mathcal {N}^\mathrm {Kra}}^\mathbb {L}$). Let us first recall the following distribution law of derived tensor product. In this section, we identify ![]() $\mathbb {V}$ with
$\mathbb {V}$ with ![]() $C$ by the isomorphism
$C$ by the isomorphism ![]() $b$ defined in (2.3).
$b$ defined in (2.3).
Lemma 3.1 Assume that ![]() $\mathcal {A}_i$ (
$\mathcal {A}_i$ (![]() $1\leq i \leq k$) is in the derived category of bounded coherent sheaves on
$1\leq i \leq k$) is in the derived category of bounded coherent sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$ and
$\mathcal {N}^\mathrm {Kra}$ and ![]() $i:\mathcal {Z}\rightarrow \mathcal {N}^\mathrm {Kra}$ is a closed embedding of formal subscheme. Then the following identity holds in the derived category of bounded coherent sheaves on
$i:\mathcal {Z}\rightarrow \mathcal {N}^\mathrm {Kra}$ is a closed embedding of formal subscheme. Then the following identity holds in the derived category of bounded coherent sheaves on ![]() $\mathcal {Z}$:
$\mathcal {Z}$:
Proof. We can take locally free representatives of ![]() $A_i^\bullet$ of
$A_i^\bullet$ of ![]() $\mathcal { A}_i$. Then
$\mathcal { A}_i$. Then ![]() $A_1^\bullet \otimes \cdots \otimes A_k^\bullet$ is again a complex of locally free sheaves on
$A_1^\bullet \otimes \cdots \otimes A_k^\bullet$ is again a complex of locally free sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$, hence a locally free representatives of
$\mathcal {N}^\mathrm {Kra}$, hence a locally free representatives of ![]() $\mathcal {A}_1\otimes ^\mathbb {L}\cdots \otimes ^\mathbb {L}\mathcal {A}_k$. Hence,
$\mathcal {A}_1\otimes ^\mathbb {L}\cdots \otimes ^\mathbb {L}\mathcal {A}_k$. Hence, ![]() $i^*(\mathcal {A}_1\otimes ^\mathbb {L}\cdots \otimes ^\mathbb {L}\mathcal {A}_k\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}})$ can be represented by
$i^*(\mathcal {A}_1\otimes ^\mathbb {L}\cdots \otimes ^\mathbb {L}\mathcal {A}_k\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}})$ can be represented by ![]() $A_1^\bullet \otimes \cdots \otimes A_k^\bullet \otimes \mathcal {O}_\mathcal {Z}$. Meanwhile
$A_1^\bullet \otimes \cdots \otimes A_k^\bullet \otimes \mathcal {O}_\mathcal {Z}$. Meanwhile ![]() $A_i^\bullet \otimes \mathcal {O}_\mathcal {Z}$ is a representative of
$A_i^\bullet \otimes \mathcal {O}_\mathcal {Z}$ is a representative of ![]() $\mathcal {A}_i\otimes ^\mathbb {L}\mathcal {O}_\mathcal {Z}$ in the derived category of bounded coherent sheaves on
$\mathcal {A}_i\otimes ^\mathbb {L}\mathcal {O}_\mathcal {Z}$ in the derived category of bounded coherent sheaves on ![]() $\mathcal {N}^\mathrm {Kra}$ and is also a complex of locally free sheaves on
$\mathcal {N}^\mathrm {Kra}$ and is also a complex of locally free sheaves on ![]() $\mathcal {Z}$. Hence
$\mathcal {Z}$. Hence ![]() $i^*(\mathcal {A}_1\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}}) \otimes _\mathcal {Z}^\mathbb {L}\cdots \otimes _\mathcal {Z}^\mathbb {L} i^*(\mathcal {A}_k\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}})$ can be represented by
$i^*(\mathcal {A}_1\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}}) \otimes _\mathcal {Z}^\mathbb {L}\cdots \otimes _\mathcal {Z}^\mathbb {L} i^*(\mathcal {A}_k\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}})$ can be represented by ![]() $(A_1^\bullet \otimes \mathcal {O}_\mathcal {Z}) \otimes _{\mathcal {Z}}\cdots \otimes _{\mathcal {Z}} (A_k^\bullet \otimes \mathcal {O}_\mathcal {Z})$. Now by the distribution law of tensor products we have
$(A_1^\bullet \otimes \mathcal {O}_\mathcal {Z}) \otimes _{\mathcal {Z}}\cdots \otimes _{\mathcal {Z}} (A_k^\bullet \otimes \mathcal {O}_\mathcal {Z})$. Now by the distribution law of tensor products we have
This finishes the proof of the lemma.
Proposition 3.2 Assume that the dimension of ![]() $\mathbb {V}$ is
$\mathbb {V}$ is ![]() $n\geq 2$. Then for each
$n\geq 2$. Then for each ![]() ${\bf x}\in \mathbb {V}$,
${\bf x}\in \mathbb {V}$, ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor. Moreover, we have the following decomposition of Cartier divisors:
$\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor. Moreover, we have the following decomposition of Cartier divisors:
where ![]() $m_\Lambda ({\bf x})$ is the largest integer
$m_\Lambda ({\bf x})$ is the largest integer ![]() $m$ such that
$m$ such that ![]() $\pi ^{-m} \cdot {\bf x}\in \Lambda$.
$\pi ^{-m} \cdot {\bf x}\in \Lambda$.
Proof. The fact that ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor is due to [Reference HowardHow19, Proposition 4.3]. By [Reference ShiShi18, Proposition 3.7], the superspecial point corresponding to a type
$\mathcal {Z}^\mathrm {Kra}({\bf x})$ is a divisor is due to [Reference HowardHow19, Proposition 4.3]. By [Reference ShiShi18, Proposition 3.7], the superspecial point corresponding to a type ![]() $0$ lattice
$0$ lattice ![]() $\Lambda$ is in
$\Lambda$ is in ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})$ if and only if
$\mathcal {Z}^\mathrm {Pap}({\bf x})$ if and only if ![]() ${\bf x} \in \Lambda$. Hence,
${\bf x} \in \Lambda$. Hence, ![]() $\mathrm {Exc}_\Lambda \subset \mathcal {Z}^\mathrm {Kra}({\bf x})$ if and only if
$\mathrm {Exc}_\Lambda \subset \mathcal {Z}^\mathrm {Kra}({\bf x})$ if and only if ![]() ${\bf x} \in \Lambda$. Since
${\bf x} \in \Lambda$. Since ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ is regular, we must have a decomposition as in (3.1) and the only job left is to determine the multiplicity of each
$\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ is regular, we must have a decomposition as in (3.1) and the only job left is to determine the multiplicity of each ![]() $\mathrm {Exc}_\Lambda$.
$\mathrm {Exc}_\Lambda$.
Fix a type ![]() $0$ lattice
$0$ lattice ![]() $\Lambda$ and let
$\Lambda$ and let ![]() $m:= m_\Lambda ({\bf x})$. Then
$m:= m_\Lambda ({\bf x})$. Then ![]() $\pi ^{-m}\cdot {\bf x}$ is a primitive vector in
$\pi ^{-m}\cdot {\bf x}$ is a primitive vector in ![]() $\Lambda$. By Lemma A.3, there exists a decomposition
$\Lambda$. By Lemma A.3, there exists a decomposition
where ![]() $\Lambda _2$ and
$\Lambda _2$ and ![]() $\Lambda '$ are unimodular lattices of rank
$\Lambda '$ are unimodular lattices of rank ![]() $2$ and
$2$ and ![]() $n-2$, respectively, and
$n-2$, respectively, and ![]() $\pi ^{-m}\cdot {\bf x}\in \Lambda _2$. Let
$\pi ^{-m}\cdot {\bf x}\in \Lambda _2$. Let ![]() $\eta =\chi (\Lambda ')$. By applying Proposition 2.6, we see that
$\eta =\chi (\Lambda ')$. By applying Proposition 2.6, we see that ![]() $\tilde {\mathcal {Z}}_{n,\epsilon }(\Lambda ')\cong \mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$. Moreover, we have the following proper intersections
$\tilde {\mathcal {Z}}_{n,\epsilon }(\Lambda ')\cong \mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$. Moreover, we have the following proper intersections
and
where ![]() $\mathrm {Exc}_{\Lambda _2}$ is the exceptional divisor in
$\mathrm {Exc}_{\Lambda _2}$ is the exceptional divisor in ![]() $\mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$ corresponding to the vertex lattice
$\mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$ corresponding to the vertex lattice ![]() $\Lambda _2$. Hence, the multiplicity of
$\Lambda _2$. Hence, the multiplicity of ![]() $\mathrm {Exc}_{\Lambda }$ in
$\mathrm {Exc}_{\Lambda }$ in ![]() $\mathcal {Z}^\mathrm {Kra}_{n,\epsilon }({\bf x})$ is the same as the multiplicity of
$\mathcal {Z}^\mathrm {Kra}_{n,\epsilon }({\bf x})$ is the same as the multiplicity of ![]() $\mathrm {Exc}_{\Lambda _2}$ in
$\mathrm {Exc}_{\Lambda _2}$ in ![]() $\mathcal {Z}^\mathrm {Kra}_{2,\epsilon \eta }({\bf x})$. Now the proposition follows from [Reference ShiShi22, Theorem 4.6] and [Reference He, Shi and YangHSY23, Theorem 4.1].
$\mathcal {Z}^\mathrm {Kra}_{2,\epsilon \eta }({\bf x})$. Now the proposition follows from [Reference ShiShi22, Theorem 4.6] and [Reference He, Shi and YangHSY23, Theorem 4.1].
The Chow ring ![]() $\mathrm {CH}^\bullet (\mathrm {Exc}_\Lambda )\cong \mathrm {Gr}^\bullet K_0(\mathrm {Exc}_\Lambda )$ is isomorphic to
$\mathrm {CH}^\bullet (\mathrm {Exc}_\Lambda )\cong \mathrm {Gr}^\bullet K_0(\mathrm {Exc}_\Lambda )$ is isomorphic to ![]() $\mathbb {Z}[H_\Lambda ]/(H_\Lambda ^{n-1}-1)$ where
$\mathbb {Z}[H_\Lambda ]/(H_\Lambda ^{n-1}-1)$ where ![]() $H_\Lambda$ is the hyperplane class of
$H_\Lambda$ is the hyperplane class of ![]() $\mathrm {Exc}_\Lambda$ represented by any
$\mathrm {Exc}_\Lambda$ represented by any ![]() $\mathbb {P}^{n-2}_k$ in
$\mathbb {P}^{n-2}_k$ in ![]() $\mathrm {Exc}_\Lambda$.
$\mathrm {Exc}_\Lambda$.
Proposition 3.3 Assume ![]() $\dim \mathbb {V} =n \geq 2$. Assume
$\dim \mathbb {V} =n \geq 2$. Assume ![]() ${\bf x}\in \mathbb {V}$ such that
${\bf x}\in \mathbb {V}$ such that ![]() $h({\bf x},{\bf x})\neq 0$ and
$h({\bf x},{\bf x})\neq 0$ and ![]() $\Lambda$ is a type
$\Lambda$ is a type ![]() $0$ vertex lattice containing
$0$ vertex lattice containing ![]() ${\bf x}$. Let
${\bf x}$. Let ![]() $m:= m_\Lambda ({\bf x})$ as in Proposition 3.2. Then
$m:= m_\Lambda ({\bf x})$ as in Proposition 3.2. Then ![]() $\tilde {\mathcal {Z}}({\bf x})$ and
$\tilde {\mathcal {Z}}({\bf x})$ and ![]() $\mathrm {Exc}_\Lambda$ intersect properly and
$\mathrm {Exc}_\Lambda$ intersect properly and
Proof. First ![]() $\tilde {\mathcal {Z}}({\bf x})$ and
$\tilde {\mathcal {Z}}({\bf x})$ and ![]() $\mathrm {Exc}_\Lambda$ are Cartier divisors with no common component, so they intersect properly. Let
$\mathrm {Exc}_\Lambda$ are Cartier divisors with no common component, so they intersect properly. Let ![]() $m=m_\Lambda ({\bf x})$ and
$m=m_\Lambda ({\bf x})$ and ![]() ${\bf x}':= \pi ^{-m}\cdot {\bf x}$. By assumption
${\bf x}':= \pi ^{-m}\cdot {\bf x}$. By assumption ![]() $m\geq 0$. By Proposition 5.9, we have
$m\geq 0$. By Proposition 5.9, we have
where ![]() $\mathrm {v}(\mathbf {y})=\mathrm {v}({\bf x}')$ and
$\mathrm {v}(\mathbf {y})=\mathrm {v}({\bf x}')$ and ![]() $\Lambda '$ is unimodular. Let
$\Lambda '$ is unimodular. Let ![]() $\eta =\chi (\Lambda ')$ and
$\eta =\chi (\Lambda ')$ and
![]() $\Lambda _2$ is rank
$\Lambda _2$ is rank ![]() $2$ unimodular and contains
$2$ unimodular and contains ![]() ${\bf x}'$.
${\bf x}'$.
By Proposition 2.6, we have ![]() $\tilde {\mathcal {Z}}(\Lambda ')\cong \mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$. In particular,
$\tilde {\mathcal {Z}}(\Lambda ')\cong \mathcal {N}_{2,\epsilon \eta }^\mathrm {Kra}$. In particular, ![]() $\tilde {\mathcal {Z}}(\Lambda ')$ is regular. By Corollary 2.7, we know that
$\tilde {\mathcal {Z}}(\Lambda ')$ is regular. By Corollary 2.7, we know that ![]() $\tilde {\mathcal {Z}}(\Lambda ')\cap \tilde {\mathcal {Z}}({\bf x})=\tilde {\mathcal {Z}}_{2,\epsilon \eta }({\bf x})$. In particular,
$\tilde {\mathcal {Z}}(\Lambda ')\cap \tilde {\mathcal {Z}}({\bf x})=\tilde {\mathcal {Z}}_{2,\epsilon \eta }({\bf x})$. In particular, ![]() $\tilde {\mathcal {Z}}(\Lambda ')$ and
$\tilde {\mathcal {Z}}(\Lambda ')$ and ![]() $\tilde {\mathcal {Z}}({\bf x})$ intersect properly as
$\tilde {\mathcal {Z}}({\bf x})$ intersect properly as ![]() $\tilde {\mathcal {Z}}_{2,\epsilon \eta }({\bf x})$ is a divisor in
$\tilde {\mathcal {Z}}_{2,\epsilon \eta }({\bf x})$ is a divisor in ![]() $\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. On the other hand,
$\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. On the other hand, ![]() $\tilde {\mathcal {Z}}(\Lambda ')\cap \mathrm {Exc}_\Lambda$ is the exceptional divisor
$\tilde {\mathcal {Z}}(\Lambda ')\cap \mathrm {Exc}_\Lambda$ is the exceptional divisor ![]() $\mathrm {Exc}_{\Lambda _2}$ in
$\mathrm {Exc}_{\Lambda _2}$ in ![]() $\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Since
$\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Since ![]() $\mathrm {Exc}_\Lambda \cong \mathbb {P}^{n-1}_k$, it is also regular. Our strategy is to compute the intersection number
$\mathrm {Exc}_\Lambda \cong \mathbb {P}^{n-1}_k$, it is also regular. Our strategy is to compute the intersection number
in two different ways. By Lemma 3.1, one way is
where we use the fact that the intersections ![]() $\tilde {\mathcal {Z}}(\Lambda ')\cap \tilde {\mathcal {Z}}({\bf x})$ and
$\tilde {\mathcal {Z}}(\Lambda ')\cap \tilde {\mathcal {Z}}({\bf x})$ and ![]() $\tilde {\mathcal {Z}}(\Lambda ')\cap \mathrm {Exc}_\Lambda$ are proper (see, for example, [Reference ZhangZha21, Lemma B.2]). The other way is, by Lemma 3.1,
$\tilde {\mathcal {Z}}(\Lambda ')\cap \mathrm {Exc}_\Lambda$ are proper (see, for example, [Reference ZhangZha21, Lemma B.2]). The other way is, by Lemma 3.1,
When ![]() $\epsilon \eta =-1$, by Proposition 3.11 and Theorem 4.5 of [Reference ShiShi22], we know that (3.2) is equal to
$\epsilon \eta =-1$, by Proposition 3.11 and Theorem 4.5 of [Reference ShiShi22], we know that (3.2) is equal to ![]() $2m+1$. When
$2m+1$. When ![]() $\epsilon \eta =1$, by Lemma 3.10, Theorem 4.1 and Lemma 5.2 of [Reference He, Shi and YangHSY23], we know that (3.2) is equal to
$\epsilon \eta =1$, by Lemma 3.10, Theorem 4.1 and Lemma 5.2 of [Reference He, Shi and YangHSY23], we know that (3.2) is equal to ![]() $2m+1$ as well. Since the intersection number of
$2m+1$ as well. Since the intersection number of ![]() $H_\Lambda$ with
$H_\Lambda$ with ![]() $\mathrm {Exc}_{\Lambda _2}\cong \mathbb {P}^1_k$ in
$\mathrm {Exc}_{\Lambda _2}\cong \mathbb {P}^1_k$ in ![]() $\mathrm {Exc}_\Lambda$ is
$\mathrm {Exc}_\Lambda$ is ![]() $1$, the proposition follows.
$1$, the proposition follows.
3.1 Intersection numbers involving the exceptional divisors
Lemma 3.4 The class of ![]() $\underbrace {\mathcal {O}_{\mathrm {Exc}_\Lambda }\otimes ^\mathbb {L} \cdots \otimes ^\mathbb {L}\mathcal {O}_{\mathrm {Exc}_\Lambda }}_{m}$ in
$\underbrace {\mathcal {O}_{\mathrm {Exc}_\Lambda }\otimes ^\mathbb {L} \cdots \otimes ^\mathbb {L}\mathcal {O}_{\mathrm {Exc}_\Lambda }}_{m}$ in ![]() $\mathrm {CH}^{m-1}(\mathrm {Exc}_\Lambda )$ is
$\mathrm {CH}^{m-1}(\mathrm {Exc}_\Lambda )$ is ![]() $(-2H_\Lambda )^{m-1}$.
$(-2H_\Lambda )^{m-1}$.
Proof. To study this intersection, it suffices to consider the local model ![]() $N^\mathrm {Kra}$ constructed in [Reference KrämerKrä03]. Let
$N^\mathrm {Kra}$ constructed in [Reference KrämerKrä03]. Let ![]() $N^\mathrm {Kra}_s$ be its special fiber. Recall by [Reference KrämerKrä03, (4.11)], we have
$N^\mathrm {Kra}_s$ be its special fiber. Recall by [Reference KrämerKrä03, (4.11)], we have
as Cartier divisors where ![]() $\mathrm {Exc}$ is the exceptional divisor of
$\mathrm {Exc}$ is the exceptional divisor of ![]() $N^\mathrm {Kra}$ and
$N^\mathrm {Kra}$ and ![]() $Z_2$ is a divisor in
$Z_2$ is a divisor in ![]() $N^\mathrm {Kra}$ which intersect properly with
$N^\mathrm {Kra}$ which intersect properly with ![]() $\mathrm {Exc}$. Their intersection is
$\mathrm {Exc}$. Their intersection is ![]() $2H$ where
$2H$ where ![]() $H$ is the hyperplane class of
$H$ is the hyperplane class of ![]() $\mathrm {Exc}$. Since
$\mathrm {Exc}$. Since ![]() $\mathrm {Exc}$ is properly supported on
$\mathrm {Exc}$ is properly supported on ![]() $N^\mathrm {Kra}$, we have
$N^\mathrm {Kra}$, we have
Hence,
 \begin{align*} 0&=[\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_{N^\mathrm{Kra}_s}]\\ &=[\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_\mathrm{Exc}]+[\mathcal{O}_\mathrm{Exc} \otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_{Z_2}]\\ &= [\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_\mathrm{Exc}]+2H. \end{align*}
\begin{align*} 0&=[\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_{N^\mathrm{Kra}_s}]\\ &=[\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_\mathrm{Exc}]+[\mathcal{O}_\mathrm{Exc} \otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_{Z_2}]\\ &= [\mathcal{O}_\mathrm{Exc}\otimes^\mathbb{L}_{N^\mathrm{Kra}} \mathcal{O}_\mathrm{Exc}]+2H. \end{align*}
This proves the lemma when ![]() $m=2$. The general case now follows from Lemma 3.1.
$m=2$. The general case now follows from Lemma 3.1.
Corollary 3.5 Let ![]() $\Lambda \in \mathcal {V}^0$ and
$\Lambda \in \mathcal {V}^0$ and ![]() ${\bf x}\in \Lambda$. Then we have the following identity in
${\bf x}\in \Lambda$. Then we have the following identity in ![]() $\mathrm {CH}^1(\mathrm {Exc}_\Lambda )$:
$\mathrm {CH}^1(\mathrm {Exc}_\Lambda )$:
Proof. By Propositions 3.2, 3.3 and Lemma 3.4, we have the following identity in ![]() $\mathrm {CH}^1(\mathrm {Exc}_\Lambda )$:
$\mathrm {CH}^1(\mathrm {Exc}_\Lambda )$:
This finishes the proof of the corollary.
Corollary 3.6 Assume that ![]() $n-m\geq 1$ and
$n-m\geq 1$ and ![]() $\mathrm {Exc}_\Lambda \subset \mathcal {Z}^\mathrm {Kra}({\bf x}_1)\cap \ldots \cap \mathcal {Z}^\mathrm {Kra}({\bf x}_m)$, then
$\mathrm {Exc}_\Lambda \subset \mathcal {Z}^\mathrm {Kra}({\bf x}_1)\cap \ldots \cap \mathcal {Z}^\mathrm {Kra}({\bf x}_m)$, then
Proof. By Corollary 3.5, Lemmas 3.1 and 3.4, we have
 \begin{align*} &\chi(\mathcal{N}_n^\mathrm{Kra},\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}_1)}\otimes^{\mathbb{L}}\ldots\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}_m)}\otimes^\mathbb{L}\underbrace{\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^{\mathbb{L}} \cdots \otimes^{\mathbb{L}} \mathcal{O}_{\mathrm{Exc}_\Lambda}}_{n-m})\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,\underbrace{(-H_\Lambda)\otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} \cdots \otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} (-H_\Lambda)}_{m}\otimes_{\mathrm{Exc}_\Lambda}^\mathbb{L}\underbrace{(-2H_\Lambda)\otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} \cdots \otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} (-2H_\Lambda)}_{n-m-1})\\ &\qquad=(-1)^m\cdot(-2)^{n-m-1}.\end{align*}
\begin{align*} &\chi(\mathcal{N}_n^\mathrm{Kra},\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}_1)}\otimes^{\mathbb{L}}\ldots\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}_m)}\otimes^\mathbb{L}\underbrace{\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^{\mathbb{L}} \cdots \otimes^{\mathbb{L}} \mathcal{O}_{\mathrm{Exc}_\Lambda}}_{n-m})\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,\underbrace{(-H_\Lambda)\otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} \cdots \otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} (-H_\Lambda)}_{m}\otimes_{\mathrm{Exc}_\Lambda}^\mathbb{L}\underbrace{(-2H_\Lambda)\otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} \cdots \otimes_{\mathrm{Exc}_\Lambda}^{\mathbb{L}} (-2H_\Lambda)}_{n-m-1})\\ &\qquad=(-1)^m\cdot(-2)^{n-m-1}.\end{align*}
□
For ![]() $\Lambda \in \mathcal {V}^0$, let
$\Lambda \in \mathcal {V}^0$, let ![]() $\mathbb {P}^1_\Lambda$ be any
$\mathbb {P}^1_\Lambda$ be any ![]() $\mathbb {P}^1_k$ in
$\mathbb {P}^1_k$ in ![]() $\mathrm {Exc}_\Lambda$, and
$\mathrm {Exc}_\Lambda$, and
Corollary 3.7 For ![]() $\Lambda \in \mathcal {V}^0$, we have
$\Lambda \in \mathcal {V}^0$, we have
Proof. By Lemma 3.4, we have
 \begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} (\mathcal{O}_{\mathrm{Exc}_\Lambda} \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}}))\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,(\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} \mathcal{O}_{\mathrm{Exc}_\Lambda}) \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=-2\chi(\mathrm{Exc}_\Lambda,H_\Lambda\cdot [\mathcal{O}_{\mathbb{P}^1_{\Lambda}}])\\ &\qquad=-2. \end{align*}
\begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} (\mathcal{O}_{\mathrm{Exc}_\Lambda} \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}}))\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,(\mathcal{O}_{\mathrm{Exc}_\Lambda}\otimes^\mathbb{L} \mathcal{O}_{\mathrm{Exc}_\Lambda}) \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=-2\chi(\mathrm{Exc}_\Lambda,H_\Lambda\cdot [\mathcal{O}_{\mathbb{P}^1_{\Lambda}}])\\ &\qquad=-2. \end{align*}
□
Corollary 3.8 For ![]() $\Lambda \in \mathcal {V}^0$, we have
$\Lambda \in \mathcal {V}^0$, we have
Proof. If ![]() ${\bf x}\notin \Lambda$, then the intersection number is apparently
${\bf x}\notin \Lambda$, then the intersection number is apparently ![]() $0$. Otherwise, by Corollary 3.5 we have
$0$. Otherwise, by Corollary 3.5 we have
 \begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x})}\otimes^\mathbb{L} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,(\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x})}\otimes^\mathbb{L} \mathcal{O}_{\mathrm{Exc}_\Lambda}) \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=-\chi(\mathrm{Exc}_\Lambda,H_\Lambda\cdot [\mathcal{O}_{\mathbb{P}^1_{\Lambda}}])\\ &\qquad=-1.\end{align*}
\begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x})}\otimes^\mathbb{L} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=\chi(\mathrm{Exc}_\Lambda,(\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x})}\otimes^\mathbb{L} \mathcal{O}_{\mathrm{Exc}_\Lambda}) \otimes_{\mathcal{O}_{\mathrm{Exc}_\Lambda}} \mathcal{O}_{\mathbb{P}^1_{\Lambda}})\\ &\qquad=-\chi(\mathrm{Exc}_\Lambda,H_\Lambda\cdot [\mathcal{O}_{\mathbb{P}^1_{\Lambda}}])\\ &\qquad=-1.\end{align*}
□
The above results suggest that the difficulty in computing ![]() $\mathrm {Int}(L)$ mainly lies in computing
$\mathrm {Int}(L)$ mainly lies in computing
We end this section by studying the intersection number of difference cycle with exceptional divisors.
Lemma 3.9 If ![]() $L^\flat$ has rank
$L^\flat$ has rank ![]() $n-1$, then for any
$n-1$, then for any ![]() $\Lambda \in \mathcal {V}^0(L^\flat )$, we have
$\Lambda \in \mathcal {V}^0(L^\flat )$, we have
 \[ \chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot [\mathcal{O}_{\mathrm{Exc}_{\Lambda}}])=\begin{cases} (-1)^{n-1}, & \text{if } L^\flat=\Lambda\cap L^\flat_F,\\ 0, & \text{otherwise}. \end{cases} \]
\[ \chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot [\mathcal{O}_{\mathrm{Exc}_{\Lambda}}])=\begin{cases} (-1)^{n-1}, & \text{if } L^\flat=\Lambda\cap L^\flat_F,\\ 0, & \text{otherwise}. \end{cases} \]
Remark 3.10 We have ![]() $L^\flat =\Lambda \cap L ^\flat _F$ if and only if
$L^\flat =\Lambda \cap L ^\flat _F$ if and only if ![]() $L^\flat$ is of type (see (4.2) and Lemma 4.3)
$L^\flat$ is of type (see (4.2) and Lemma 4.3) ![]() $1$ or
$1$ or ![]() $0$ and
$0$ and ![]() $\Lambda$ is at the boundary of the
$\Lambda$ is at the boundary of the ![]() $\mathcal {L}(L^\flat )$.
$\mathcal {L}(L^\flat )$.
Proof. Define
Then for ![]() $L'$ such that
$L'$ such that ![]() $L^\flat \subset L'\subset ({1}/{\pi }) L^\flat$, we know that
$L^\flat \subset L'\subset ({1}/{\pi }) L^\flat$, we know that ![]() $\mathcal {Z}^\mathrm {Kra}(L')$ intersects
$\mathcal {Z}^\mathrm {Kra}(L')$ intersects ![]() $\mathrm {Exc}_{\Lambda }$ if and only if
$\mathrm {Exc}_{\Lambda }$ if and only if ![]() $L'\subset M'$. For such
$L'\subset M'$. For such ![]() $L'$, by Corollary 3.6, we have
$L'$, by Corollary 3.6, we have
Hence,
 \[
\chi\big(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot
[\mathcal{O}_{\mathrm{Exc}_{\Lambda}}]\big)=(-1)^{n-1}\biggl[1+\sum_{i=1}^m (-1)^i q^{i(i-1)/2}
\sum_{\substack{L^\flat\subset L'\subset M'\\
\mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} 1\biggr].
\]
\[
\chi\big(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot
[\mathcal{O}_{\mathrm{Exc}_{\Lambda}}]\big)=(-1)^{n-1}\biggl[1+\sum_{i=1}^m (-1)^i q^{i(i-1)/2}
\sum_{\substack{L^\flat\subset L'\subset M'\\
\mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} 1\biggr].
\]
Note that ![]() $m=0$ if and only if
$m=0$ if and only if ![]() $M'=L^\flat$ which is equivalent to the condition
$M'=L^\flat$ which is equivalent to the condition ![]() $L^\flat =\Lambda \cap L^\flat _F$. In this case the summation in (4.8) is over an empty set, hence (4.8) is equal to
$L^\flat =\Lambda \cap L^\flat _F$. In this case the summation in (4.8) is over an empty set, hence (4.8) is equal to ![]() $1$. If
$1$. If ![]() $m>0$ we know (4.8) is equal to
$m>0$ we know (4.8) is equal to ![]() $0$ by (2.13).
$0$ by (2.13).
4. Horizontal components of special cycles
Given an integral Hermitian lattice ![]() $L$, we can have its Jordan decomposition:
$L$, we can have its Jordan decomposition:
where ![]() $L_t$ is
$L_t$ is ![]() $\pi ^t$-modular, see [Reference JacobowitzJac62]. Define the type of
$\pi ^t$-modular, see [Reference JacobowitzJac62]. Define the type of ![]() $L$ to be
$L$ to be
4.1 Quasi-canonical lifting cycles
Assume that ![]() $\mathrm {dim}(\mathbb {V})=2$. When
$\mathrm {dim}(\mathbb {V})=2$. When ![]() $\chi (\mathbb {V})=-1$, for
$\chi (\mathbb {V})=-1$, for ![]() $\mathbf {y}\in \mathbb {V}$, by [Reference ShiShi22, Theorem 4.5], we have the following equality of Cartier divisors on
$\mathbf {y}\in \mathbb {V}$, by [Reference ShiShi22, Theorem 4.5], we have the following equality of Cartier divisors on ![]() $\mathcal {N}_{2,-1}^\mathrm {Kra}$:
$\mathcal {N}_{2,-1}^\mathrm {Kra}$:
 \[ \tilde{\mathcal{Z}}_{2,-1}(\mathbf{y})=\mathcal{Z}_0+\sum_{s=1}^{\mathrm{v}(\mathbf{y})} (\mathcal{Z}_{s}^+ +\mathcal{Z}_{s}^-). \]
\[ \tilde{\mathcal{Z}}_{2,-1}(\mathbf{y})=\mathcal{Z}_0+\sum_{s=1}^{\mathrm{v}(\mathbf{y})} (\mathcal{Z}_{s}^+ +\mathcal{Z}_{s}^-). \]
Here ![]() $\mathcal {Z}_0$ (respectively,
$\mathcal {Z}_0$ (respectively, ![]() $\mathcal {Z}_{s}^{\pm }$) is a canonical (respectively, quasi-canonical) lifting cycle of level
$\mathcal {Z}_{s}^{\pm }$) is a canonical (respectively, quasi-canonical) lifting cycle of level ![]() $0$ (respectively,
$0$ (respectively, ![]() $s$), see [Reference ShiShi22, § 3]. Moreover by [Reference ShiShi22, Proposition 3.12],
$s$), see [Reference ShiShi22, § 3]. Moreover by [Reference ShiShi22, Proposition 3.12], ![]() $\mathcal {Z}_s^+$ and
$\mathcal {Z}_s^+$ and ![]() $\mathcal {Z}_s^-$ do not intersect when
$\mathcal {Z}_s^-$ do not intersect when ![]() $s\geq 1$. Let
$s\geq 1$. Let ![]() $\mathcal {O}_s:=\mathcal {O}_{F_0}+\mathcal {O}_{F}\cdot \pi _0^s$ and
$\mathcal {O}_s:=\mathcal {O}_{F_0}+\mathcal {O}_{F}\cdot \pi _0^s$ and ![]() $M_s$ be the finite abelian extension of
$M_s$ be the finite abelian extension of ![]() ${\breve F}$ corresponding to the subgroup
${\breve F}$ corresponding to the subgroup ![]() $\mathcal {O}_s^\times$ under local class field theory. Let
$\mathcal {O}_s^\times$ under local class field theory. Let ![]() $W_s$ be the integral closure of
$W_s$ be the integral closure of ![]() $\mathcal {O}_{\breve F}$ in
$\mathcal {O}_{\breve F}$ in ![]() $M_s$. Then we have
$M_s$. Then we have ![]() $\mathcal {Z}_0\cong {\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ and
$\mathcal {Z}_0\cong {\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ and ![]() $\mathcal {Z}_{s}^{\pm }\cong \mathrm {Spf}\, W_s$. Define the primitive part of
$\mathcal {Z}_{s}^{\pm }\cong \mathrm {Spf}\, W_s$. Define the primitive part of ![]() $\tilde {\mathcal {Z}}_{2,-1}(\mathbf {y})$ to be
$\tilde {\mathcal {Z}}_{2,-1}(\mathbf {y})$ to be
When ![]() $\chi (\mathbb {V})=1$, for
$\chi (\mathbb {V})=1$, for ![]() $\mathbf {y}\in \mathbb {V}$ such that
$\mathbf {y}\in \mathbb {V}$ such that ![]() $\mathrm {v}(\mathbf {y})\geq 0$, by [Reference He, Shi and YangHSY23, Theorem 4.1], we have the following equality of Cartier divisors on
$\mathrm {v}(\mathbf {y})\geq 0$, by [Reference He, Shi and YangHSY23, Theorem 4.1], we have the following equality of Cartier divisors on ![]() $\mathcal {N}_{2,1}^\mathrm {Kra}$:
$\mathcal {N}_{2,1}^\mathrm {Kra}$:
where ![]() $\mathcal {Z}_0\cong {\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ is a canonical lifting cycle and
$\mathcal {Z}_0\cong {\mathrm {Spf}\,\mathcal {O}_{\breve {F}} }$ is a canonical lifting cycle and ![]() $\mathcal {Z}_v(\mathbf {y})$ is a Cartier divisor whose structure sheaf is annihilated by
$\mathcal {Z}_v(\mathbf {y})$ is a Cartier divisor whose structure sheaf is annihilated by ![]() $\pi ^N$ for some
$\pi ^N$ for some ![]() $N> 0$. Define the primitive horizontal part of
$N> 0$. Define the primitive horizontal part of ![]() $\tilde {\mathcal {Z}}_{2,1}(\mathbf {y})$ as
$\tilde {\mathcal {Z}}_{2,1}(\mathbf {y})$ as
4.2 Horizontal cycles
Definition 4.1 Let ![]() $M^\flat$ be a rank
$M^\flat$ be a rank ![]() $n-1$ integral lattice in
$n-1$ integral lattice in ![]() $\mathbb {V}$. We say that
$\mathbb {V}$. We say that ![]() $M^\flat$ is horizontal if one of the following conditions is satisfied:
$M^\flat$ is horizontal if one of the following conditions is satisfied:
(1)
 $M^\flat$ is unimodular;
$M^\flat$ is unimodular;(2)
 $M^\flat$ is of the form
$M^\flat$ is of the form  $M^\flat =M{\unicode{x29BA}} \mathrm {Span}\{\mathbf {y}\}$ where
$M^\flat =M{\unicode{x29BA}} \mathrm {Span}\{\mathbf {y}\}$ where  $M$ is a unimodular sublattice of rank
$M$ is a unimodular sublattice of rank  $n-2$ such that
$n-2$ such that  $(M_F)^\bot$ (the perpendicular complement of
$(M_F)^\bot$ (the perpendicular complement of  $M_F$ in
$M_F$ in  $\mathbb {V}$) is non-split.
$\mathbb {V}$) is non-split.
Note that condition (2) is independent of the choice of ![]() $M$. We denote the set of horizontal lattices by
$M$. We denote the set of horizontal lattices by ![]() $\mathrm {Hor}$.
$\mathrm {Hor}$.
For a rank ![]() $n-1$ integral lattice
$n-1$ integral lattice ![]() $L^\flat$, define
$L^\flat$, define
Let ![]() $M^\flat \subset \mathbb {V}$ be a lattice of rank
$M^\flat \subset \mathbb {V}$ be a lattice of rank ![]() $n-1$ and type
$n-1$ and type ![]() $1$ or
$1$ or ![]() $0$. We can decompose
$0$. We can decompose ![]() $M^\flat$ as
$M^\flat$ as
for some unimodular lattice ![]() $M$ of rank
$M$ of rank ![]() $n-2$. Then Proposition 2.6 and its corollary imply that
$n-2$. Then Proposition 2.6 and its corollary imply that
Under this isomorphism, define ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ to be the formal subscheme of
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ to be the formal subscheme of ![]() $\tilde {\mathcal {Z}}(M^\flat )$ isomorphic to
$\tilde {\mathcal {Z}}(M^\flat )$ isomorphic to ![]() $\tilde {\mathcal {Z}}_{2,\chi ((M_F)^\bot )}(\mathbf {y})^\circ$. By the discussion in § 4.1,
$\tilde {\mathcal {Z}}_{2,\chi ((M_F)^\bot )}(\mathbf {y})^\circ$. By the discussion in § 4.1, ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ is nonempty if and only if
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ is nonempty if and only if ![]() $M^\flat \in \mathrm {Hor}$, in which case it consists of the union of irreducible components of
$M^\flat \in \mathrm {Hor}$, in which case it consists of the union of irreducible components of ![]() $\tilde {\mathcal {Z}}(M^\flat )$ isomorphic to
$\tilde {\mathcal {Z}}(M^\flat )$ isomorphic to ![]() $\mathrm {Spf}\, W_s$. In particular,
$\mathrm {Spf}\, W_s$. In particular, ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ is independent of the choice of
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ is independent of the choice of ![]() $M$.
$M$.
Theorem 4.2 Let ![]() $L^\flat$ be a rank
$L^\flat$ be a rank ![]() $n-1$ integral lattice in
$n-1$ integral lattice in ![]() $\mathbb {V}$, then
$\mathbb {V}$, then
In particular, ![]() $\mathcal {Z}^{\mathrm {Kra}}(L^\flat )_h$ is of pure dimension
$\mathcal {Z}^{\mathrm {Kra}}(L^\flat )_h$ is of pure dimension ![]() $1$. Moreover, we have the following identity in
$1$. Moreover, we have the following identity in ![]() $\mathrm {Gr}^{n-1}K_0(\mathcal {N}^\mathrm {Kra})$:
$\mathrm {Gr}^{n-1}K_0(\mathcal {N}^\mathrm {Kra})$:
Proof. The proof largely follows [Reference Li and ZhangLZ22a, § 4.4]. Let ![]() $K$ be a finite extension of
$K$ be a finite extension of ![]() $\breve F$. Assume that
$\breve F$. Assume that ![]() $z$ is an irreducible component of
$z$ is an irreducible component of ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )(\mathcal {O}_K)=\mathcal {Z}^\mathrm {Pap}(L^\flat )(\mathcal {O}_K)$, and let
$\mathcal {Z}^\mathrm {Kra}(L^\flat )(\mathcal {O}_K)=\mathcal {Z}^\mathrm {Pap}(L^\flat )(\mathcal {O}_K)$, and let ![]() $G$ be the corresponding formal
$G$ be the corresponding formal ![]() $\mathcal {O}_F$-module over
$\mathcal {O}_F$-module over ![]() $\mathcal {O}_K$. Define
$\mathcal {O}_K$. Define
where ![]() $\mathcal {G}$ is the canonical lifting and
$\mathcal {G}$ is the canonical lifting and ![]() $T_p$ is the integral
$T_p$ is the integral ![]() $p$-adic Tate module. Here
$p$-adic Tate module. Here ![]() $L$ is an
$L$ is an ![]() $\mathcal {O}_F$-module of rank
$\mathcal {O}_F$-module of rank ![]() $n$ equipped with the Hermitian form
$n$ equipped with the Hermitian form
under which it is self-dual. We have two inclusions (preserving Hermitian forms)
and
By Lemma 4.4.1 of [Reference Li and ZhangLZ22a], we have
Let
Then ![]() $z \subset \mathcal {Z}(M^\flat )(\mathcal {O}_K)$. Lemma 4.3 below implies that
$z \subset \mathcal {Z}(M^\flat )(\mathcal {O}_K)$. Lemma 4.3 below implies that ![]() $t(M^\flat )\leq 1$. Hence, we know that
$t(M^\flat )\leq 1$. Hence, we know that ![]() $z$ is one of the irreducible component of
$z$ is one of the irreducible component of ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ \cong \tilde {\mathcal {Z}}_{2,\chi ((M_F)^\bot )}(\mathbf {y})$ assuming the decomposition of
$\tilde {\mathcal {Z}}(M^\flat )^\circ \cong \tilde {\mathcal {Z}}_{2,\chi ((M_F)^\bot )}(\mathbf {y})$ assuming the decomposition of ![]() $M^\flat$ as in (4.4). The non-emptiness of
$M^\flat$ as in (4.4). The non-emptiness of ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ implies that
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ implies that ![]() $M^\flat \in \mathrm {Hor}$. It remains to prove that
$M^\flat \in \mathrm {Hor}$. It remains to prove that ![]() $z$ has multiplicity
$z$ has multiplicity ![]() $1$ in
$1$ in ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )$. Consider
$\mathcal {Z}^\mathrm {Kra}(L^\flat )$. Consider ![]() $R$-points of both sides of (4.5), where
$R$-points of both sides of (4.5), where ![]() $R:= \mathcal {O}_K[x]/(x^2)$. As in [Reference KrämerKrä03] (see [Reference Rapoport and ZinkRZ96, Appendix of Chapter 3]) we know
$R:= \mathcal {O}_K[x]/(x^2)$. As in [Reference KrämerKrä03] (see [Reference Rapoport and ZinkRZ96, Appendix of Chapter 3]) we know
where ![]() $\mathbb {D}$ is the
$\mathbb {D}$ is the ![]() $\mathcal {O}_{F_0}$-relative Dieudonné crystal. Define
$\mathcal {O}_{F_0}$-relative Dieudonné crystal. Define
Then the Hodge submodule ![]() $\mathcal {F}_0$ of
$\mathcal {F}_0$ of ![]() $\mathbb {D}(\mathcal {G})(R)$ is spanned by
$\mathbb {D}(\mathcal {G})(R)$ is spanned by
Here ![]() $\mathbb {D}(G)(R)$ is equipped with an
$\mathbb {D}(G)(R)$ is equipped with an ![]() $\mathcal {O}_F$-invariant symplectic form
$\mathcal {O}_F$-invariant symplectic form ![]() $\langle,\rangle$ and we can assume that
$\langle,\rangle$ and we can assume that ![]() $\mathbb {D}(G)(R)$ has a basis
$\mathbb {D}(G)(R)$ has a basis ![]() $\{\tilde {e}_1,\ldots,\tilde {e}_n,\tilde {f}_1,\ldots,\tilde {f}_n\}$ such that
$\{\tilde {e}_1,\ldots,\tilde {e}_n,\tilde {f}_1,\ldots,\tilde {f}_n\}$ such that
Since any element in ![]() $L^\flat$ is
$L^\flat$ is ![]() $\mathcal {O}_F$-linear, we can arrange a change of basis if necessary and assume that
$\mathcal {O}_F$-linear, we can arrange a change of basis if necessary and assume that
Now ![]() $\mathbb {D}(G)(\mathcal {O}_K)=\mathbb {D}(G)(R)\otimes _R \mathcal {O}_K$. Let
$\mathbb {D}(G)(\mathcal {O}_K)=\mathbb {D}(G)(R)\otimes _R \mathcal {O}_K$. Let ![]() $e_i=\tilde {e}_i\otimes 1$ and
$e_i=\tilde {e}_i\otimes 1$ and ![]() $f_i=\tilde {f}_i\otimes 1$ respectively. There is an exact sequence of free
$f_i=\tilde {f}_i\otimes 1$ respectively. There is an exact sequence of free ![]() $\mathcal {O}_{F}\otimes _{\mathcal {O}_{F_0}}\mathcal {O}_K$-modules (the Hodge filtration)
$\mathcal {O}_{F}\otimes _{\mathcal {O}_{F_0}}\mathcal {O}_K$-modules (the Hodge filtration)
where ![]() $\mathrm {Fil}$ is isotropic with respect to
$\mathrm {Fil}$ is isotropic with respect to ![]() $\langle,\rangle$. We must have
$\langle,\rangle$. We must have ![]() $L^\flat ((1\otimes \pi )e_0+f_0)\subset \mathrm {Fil}$. Hence, we have
$L^\flat ((1\otimes \pi )e_0+f_0)\subset \mathrm {Fil}$. Hence, we have
Since ![]() $\mathrm {Fil}$ is isotropic and by the signature condition, we have
$\mathrm {Fil}$ is isotropic and by the signature condition, we have
Since ![]() $(x)\subset R$ has a nilpotent positive-definite structure, by Grothendieck–Messing theory, a lift
$(x)\subset R$ has a nilpotent positive-definite structure, by Grothendieck–Messing theory, a lift ![]() $\tilde {z}$ of
$\tilde {z}$ of ![]() $z$ to
$z$ to ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )(R)$ corresponds to a lift of
$\mathcal {Z}^\mathrm {Kra}(L^\flat )(R)$ corresponds to a lift of ![]() $\mathrm {Fil}$ to an isotropic
$\mathrm {Fil}$ to an isotropic ![]() $\mathcal {O}_F\otimes _{\mathcal {O}_{F_0}}R$-module
$\mathcal {O}_F\otimes _{\mathcal {O}_{F_0}}R$-module ![]() $\widetilde {\mathrm {Fil}}$ in
$\widetilde {\mathrm {Fil}}$ in ![]() $\mathbb {D}(G)(R)$ containing the image of
$\mathbb {D}(G)(R)$ containing the image of ![]() $L^\flat$. By the same reasoning as above, we must have
$L^\flat$. By the same reasoning as above, we must have
Hence, such lift is unique. This implies that the multiplicity of ![]() $z$ in
$z$ in ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is one.
$\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is one.
Lemma 4.3 Let ![]() $L$ be a self-dual Hermitian lattice of rank
$L$ be a self-dual Hermitian lattice of rank ![]() $n$ and
$n$ and ![]() $W$ be a
$W$ be a ![]() $n-1$ dimensional subspace of
$n-1$ dimensional subspace of ![]() $L_F$. Then
$L_F$. Then ![]() $t(M^\flat )\le 1$ for
$t(M^\flat )\le 1$ for ![]() $M^\flat =L\cap W$.
$M^\flat =L\cap W$.
Proof. This is exactly the same as the proof of [Reference Li and ZhangLZ22a, Lemma 4.5.1]. Note that in our case we may need some blocks ![]() $\bigl (\begin {smallmatrix} 0 & \pi ^a \\ (-\pi )^a & 0\end {smallmatrix}\bigr )$ in the upper left
$\bigl (\begin {smallmatrix} 0 & \pi ^a \\ (-\pi )^a & 0\end {smallmatrix}\bigr )$ in the upper left ![]() $(n-1)\times (n-1)$ block of
$(n-1)\times (n-1)$ block of ![]() $T$ as in [Reference Li and ZhangLZ22a]. Alternatively, see [Reference Li and LiuLL22, Lemma 2.24(2)].
$T$ as in [Reference Li and ZhangLZ22a]. Alternatively, see [Reference Li and LiuLL22, Lemma 2.24(2)].
We end this subsection with the following lemma.
Lemma 4.4 Assume ![]() $M^\flat \in \mathrm {Hor}$. Then
$M^\flat \in \mathrm {Hor}$. Then ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ intersects the special fiber of
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ intersects the special fiber of ![]() $\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ at a unique
$\mathcal {N}_{n,\epsilon }^\mathrm {Kra}$ at a unique ![]() $\mathrm {Exc}_\Lambda$ for some
$\mathrm {Exc}_\Lambda$ for some ![]() $\Lambda \in \mathcal {V}^0$. Moreover,
$\Lambda \in \mathcal {V}^0$. Moreover,
 \[ \chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{Z}}(M^\flat)^\circ}\otimes^{\mathbb{L}} \mathcal{O}_{\mathrm{Exc}_\Lambda})=\begin{cases} 1, & \text{if } M^\flat \text{ is unimodular}, \\ 2, & \text{otherwise}. \end{cases} \]
\[ \chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{Z}}(M^\flat)^\circ}\otimes^{\mathbb{L}} \mathcal{O}_{\mathrm{Exc}_\Lambda})=\begin{cases} 1, & \text{if } M^\flat \text{ is unimodular}, \\ 2, & \text{otherwise}. \end{cases} \]
Proof. By the definition of ![]() $\mathrm {Hor}$, we can find a decomposition of
$\mathrm {Hor}$, we can find a decomposition of ![]() $M^\flat$
$M^\flat$
such that ![]() $M$ is self-dual. Let
$M$ is self-dual. Let ![]() $\Lambda$ be any vertex lattice containing
$\Lambda$ be any vertex lattice containing ![]() $M^\flat$. If
$M^\flat$. If ![]() $M^\flat$ is unimodular, then
$M^\flat$ is unimodular, then ![]() $\Lambda$ has to be of the form
$\Lambda$ has to be of the form ![]() $M^\flat {\unicode{x29BA}} L'$ where
$M^\flat {\unicode{x29BA}} L'$ where ![]() $L'$ is the unique unimodular lattice in
$L'$ is the unique unimodular lattice in ![]() $(M^\flat _F)^\bot$. If
$(M^\flat _F)^\bot$. If ![]() $M^\flat$ is of the form
$M^\flat$ is of the form ![]() $M{\unicode{x29BA}} L'$ such that
$M{\unicode{x29BA}} L'$ such that ![]() $M$ is of rank
$M$ is of rank ![]() $n-2$ and
$n-2$ and ![]() $(M_F)^\bot$ is non-split, then the proof of [Reference ShiShi18, Theorem 3.10] implies that there is a unique vertex lattice
$(M_F)^\bot$ is non-split, then the proof of [Reference ShiShi18, Theorem 3.10] implies that there is a unique vertex lattice ![]() $\Lambda '$ in
$\Lambda '$ in ![]() $(M_F)^\bot$ which is of unimodular (this fact is the same as the fact that the Bruhat–Tits building of
$(M_F)^\bot$ which is of unimodular (this fact is the same as the fact that the Bruhat–Tits building of ![]() $(M_F)^\bot$ has only one point). Then
$(M_F)^\bot$ has only one point). Then ![]() $\Lambda$ must be of the form
$\Lambda$ must be of the form ![]() $M{\unicode{x29BA}} \Lambda '$. In both cases,
$M{\unicode{x29BA}} \Lambda '$. In both cases, ![]() $\Lambda$ is unique and is of type
$\Lambda$ is unique and is of type ![]() $0$.
$0$.
Assume ![]() $\chi (M)=\eta$. By Proposition 2.6,
$\chi (M)=\eta$. By Proposition 2.6, ![]() $\tilde {\mathcal {Z}}(M)\cong \mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Moreover,
$\tilde {\mathcal {Z}}(M)\cong \mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Moreover, ![]() $\tilde {\mathcal {Z}}(M)\cap \mathrm {Exc}_{\Lambda }=\mathbb {P}^1_k$ is an exceptional divisor in
$\tilde {\mathcal {Z}}(M)\cap \mathrm {Exc}_{\Lambda }=\mathbb {P}^1_k$ is an exceptional divisor in ![]() $\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Hence, by Lemma 3.1, we have
$\mathcal {N}^\mathrm {Kra}_{2,\epsilon \eta }$. Hence, by Lemma 3.1, we have
Now the lemma follows from [Reference He, Shi and YangHSY23, Lemma 5.2] when ![]() $\epsilon \eta =1$, and from [Reference ShiShi22, Proposition 3.11] when
$\epsilon \eta =1$, and from [Reference ShiShi22, Proposition 3.11] when ![]() $\epsilon \eta =-1$.
$\epsilon \eta =-1$.
4.3 The horizontal part of special difference cycles
Definition 2.15 motivates us to make the following definition.
Definition 4.5 When ![]() $L^\flat$ is a rank
$L^\flat$ is a rank ![]() $n-1$ integral lattice, define
$n-1$ integral lattice, define ![]() $\mathcal {D}(L^\flat )_h\in \mathrm {Gr}^{n-1} K_0(\mathcal {N}^\mathrm {Kra})$ by
$\mathcal {D}(L^\flat )_h\in \mathrm {Gr}^{n-1} K_0(\mathcal {N}^\mathrm {Kra})$ by
 \begin{equation} \mathcal{D}(L^\flat)_h=[\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(L^\flat)_h}]+\sum_{i=1}^{n-1} (-1)^i q^{i(i-1)/2} \sum_{\substack{L^\flat\subset L'\subset \frac{1}{\pi} L^\flat\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} [\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(L')_h}]. \end{equation}
\begin{equation} \mathcal{D}(L^\flat)_h=[\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(L^\flat)_h}]+\sum_{i=1}^{n-1} (-1)^i q^{i(i-1)/2} \sum_{\substack{L^\flat\subset L'\subset \frac{1}{\pi} L^\flat\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} [\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(L')_h}]. \end{equation}Proposition 4.6 Assume ![]() $L^\flat$ is a rank
$L^\flat$ is a rank ![]() $n-1$ integral lattice, then
$n-1$ integral lattice, then
 \[ \mathcal{D}(L^\flat)_h=\begin{cases} \tilde{\mathcal{Z}}(L^\flat)^\circ, & \text{if } L^\flat\in \mathrm{Hor},\\ 0 , & \text{if } L^\flat\notin \mathrm{Hor}. \end{cases} \]
\[ \mathcal{D}(L^\flat)_h=\begin{cases} \tilde{\mathcal{Z}}(L^\flat)^\circ, & \text{if } L^\flat\in \mathrm{Hor},\\ 0 , & \text{if } L^\flat\notin \mathrm{Hor}. \end{cases} \]
Proof. By Theorem 4.2, it suffices to compute the multiplicity of an irreducible component in ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ in
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ in ![]() $\mathcal {D}(L)_h$ for all
$\mathcal {D}(L)_h$ for all ![]() $M^\flat \in \mathrm {Hor}(L^\flat )$ (see (4.3)). For such a
$M^\flat \in \mathrm {Hor}(L^\flat )$ (see (4.3)). For such a ![]() $M^\flat$, define
$M^\flat$, define
Then for a lattice ![]() $L'$ with
$L'$ with ![]() $L^\flat \subset L'\subset ({1}/{\pi }) L^\flat$, we know that
$L^\flat \subset L'\subset ({1}/{\pi }) L^\flat$, we know that ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ is in
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ is in ![]() $\mathcal {Z}^\mathrm {Kra}(L')_h$ if and only if
$\mathcal {Z}^\mathrm {Kra}(L')_h$ if and only if ![]() $L'\subset M'$. Hence, the multiplicity of an irreducible components in
$L'\subset M'$. Hence, the multiplicity of an irreducible components in ![]() $\tilde {\mathcal {Z}}(M^\flat )^\circ$ in
$\tilde {\mathcal {Z}}(M^\flat )^\circ$ in ![]() $\mathcal {D}(L)_h$ is
$\mathcal {D}(L)_h$ is
 \begin{equation} 1+\sum_{i=1}^m (-1)^i q^{i(i-1)/2} \sum_{\substack{L^\flat\subset L'\subset M'\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} 1. \end{equation}
\begin{equation} 1+\sum_{i=1}^m (-1)^i q^{i(i-1)/2} \sum_{\substack{L^\flat\subset L'\subset M'\\ \mathrm{dim}_{\mathbb{F}_q}(L'/L^\flat)=i}} 1. \end{equation}
Note that ![]() $m=0$ if and only if
$m=0$ if and only if ![]() $M'=M^\flat =L^\flat$, in this case the summation in (4.8) is over an empty set, hence (4.8) is equal to
$M'=M^\flat =L^\flat$, in this case the summation in (4.8) is over an empty set, hence (4.8) is equal to ![]() $1$. If
$1$. If ![]() $m>0$, (4.8) is equal to
$m>0$, (4.8) is equal to ![]() $0$ by (2.13).
$0$ by (2.13).
Part 2. The analytic side
5. Induction formula and primitive local density
In this section, we study various induction formulas of local density polynomials. Let ![]() $M$ be a Hermitian
$M$ be a Hermitian ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $m$ with
$m$ with ![]() $\mathrm {v}(M):= \min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in M\} \ge -1$. and let
$\mathrm {v}(M):= \min \{\mathrm {v}_\pi ( h(v,v'))\mid v,v'\in M\} \ge -1$. and let ![]() $M^{[k]}= \mathcal {H}^k{\unicode{x29BA}} M$ for an integer
$M^{[k]}= \mathcal {H}^k{\unicode{x29BA}} M$ for an integer ![]() $k \ge 0$. Let
$k \ge 0$. Let ![]() $L$ be a Hermitian
$L$ be a Hermitian ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $n$.
$n$.
There is a polynomial ![]() $\alpha (M, L, X)$ of
$\alpha (M, L, X)$ of ![]() $X$, the local density polynomial, such that
$X$, the local density polynomial, such that
where ![]() $T({\bf x})$ is the moment matrix of
$T({\bf x})$ is the moment matrix of ![]() ${\bf x}$,
${\bf x}$, ![]() $d{\bf x}$ is the Haar measure on
$d{\bf x}$ is the Haar measure on ![]() $(M^{[k]})^n$ with total volume
$(M^{[k]})^n$ with total volume ![]() $1$,
$1$, ![]() $dY$ is the Haar measures on
$dY$ is the Haar measures on ![]() $\mathrm {Herm}_n(F)$ such that
$\mathrm {Herm}_n(F)$ such that ![]() $\mathrm {Herm}_n(\mathcal {O}_{F})$ has total volume
$\mathrm {Herm}_n(\mathcal {O}_{F})$ has total volume ![]() $1$ and
$1$ and ![]() $\psi$ is an additive character of
$\psi$ is an additive character of ![]() $F_0$ with conductor
$F_0$ with conductor ![]() $\mathcal {O}_{F_0}$. Finally, we define
$\mathcal {O}_{F_0}$. Finally, we define ![]() $\langle X,Y\rangle =\mathrm {Tr}(XY)$ on
$\langle X,Y\rangle =\mathrm {Tr}(XY)$ on ![]() $\mathrm {Herm}_n$. We also use the notation
$\mathrm {Herm}_n$. We also use the notation ![]() $\alpha (M, L)=\alpha (M, L, 1)$ and
$\alpha (M, L)=\alpha (M, L, 1)$ and
There is another way to define ![]() $\alpha (M,L,X)$ as follows. We use
$\alpha (M,L,X)$ as follows. We use ![]() $\mathrm {Herm}_{L,M}$ to denote the scheme of Hermitian
$\mathrm {Herm}_{L,M}$ to denote the scheme of Hermitian ![]() $\mathcal {O}_F$-module homomorphisms from
$\mathcal {O}_F$-module homomorphisms from ![]() $L$ to
$L$ to ![]() $M$, which is a scheme of finite type over
$M$, which is a scheme of finite type over ![]() $\mathcal {O}_{F_0}$. More specifically, for an
$\mathcal {O}_{F_0}$. More specifically, for an ![]() $\mathcal {O}_{F_0}$-algebra
$\mathcal {O}_{F_0}$-algebra ![]() $R$, we define
$R$, we define
Then
To simplify the notation, we let
Then a direct calculation as in [Reference ShiShi22, Lemma 6.1] shows that
for sufficiently large integers ![]() $d >0$. Since
$d >0$. Since ![]() $\alpha (M,L, X)$ only depends on the Gram matrices of
$\alpha (M,L, X)$ only depends on the Gram matrices of ![]() $M$ and
$M$ and ![]() $L$, we may also denote it by
$L$, we may also denote it by ![]() $\alpha (S, T, X)$ if
$\alpha (S, T, X)$ if ![]() $S$ and
$S$ and ![]() $T$ are the Gram matrices of
$T$ are the Gram matrices of ![]() $M$ and
$M$ and ![]() $L$.
$L$.
Now we define primitive local density polynomials. For ![]() $1 \le \ell \le n$, let
$1 \le \ell \le n$, let
For ![]() $L=L_1\oplus L_2$, where
$L=L_1\oplus L_2$, where ![]() $L_1=\mathrm {Span}\{l_1,\ldots,l_{\ell }\}$ and
$L_1=\mathrm {Span}\{l_1,\ldots,l_{\ell }\}$ and ![]() $L_2=\mathrm {Span}\{l_{\ell +1},\ldots,l_n\}$, we define the local
$L_2=\mathrm {Span}\{l_{\ell +1},\ldots,l_n\}$, we define the local ![]() $\ell$-primitive density to be
$\ell$-primitive density to be
When ![]() $\ell \not = n$, the above definition depends on a choice of
$\ell \not = n$, the above definition depends on a choice of ![]() $L=L_1\oplus L_2$. Hence, we always fix such a decomposition
$L=L_1\oplus L_2$. Hence, we always fix such a decomposition ![]() $L=L_1\oplus L_2$ in this case. When
$L=L_1\oplus L_2$ in this case. When ![]() $L=L_1{\unicode{x29BA}} L_2$, and
$L=L_1{\unicode{x29BA}} L_2$, and ![]() $L_i$ is represented by
$L_i$ is represented by ![]() $T_i$, we also denote
$T_i$, we also denote ![]() $\beta (M, L_1{\unicode{x29BA}} L_2)^{(\ell )}$ as
$\beta (M, L_1{\unicode{x29BA}} L_2)^{(\ell )}$ as ![]() $\beta (S, \mathrm {Diag}(T_1,T_2))^{(\ell )}$. When
$\beta (S, \mathrm {Diag}(T_1,T_2))^{(\ell )}$. When ![]() $\ell =n$, we simply denote
$\ell =n$, we simply denote ![]() $\beta (M, L_1\oplus L_2)^{(\ell )}$ as
$\beta (M, L_1\oplus L_2)^{(\ell )}$ as ![]() $\beta (M,L)$.
$\beta (M,L)$.
Lemma 5.1 Assume ![]() $L=L_1 \oplus L_2$ where
$L=L_1 \oplus L_2$ where ![]() $\mathrm {rank}(L_1)=n_1$. Then
$\mathrm {rank}(L_1)=n_1$. Then
where ![]() $\ell (L_1'/L_1)=\mathrm {length}_{\mathcal {O}_F}L_1'/L_1$.
$\ell (L_1'/L_1)=\mathrm {length}_{\mathcal {O}_F}L_1'/L_1$.
Proof. This is the analogue of [Reference KitaokaKit83, Lemma 3]. Let ![]() $G=\mathrm {GL}_{n_1}(F)\cap \mathrm {M}_{n_1}(\mathcal {O}_F)$ and
$G=\mathrm {GL}_{n_1}(F)\cap \mathrm {M}_{n_1}(\mathcal {O}_F)$ and ![]() $U=\mathrm {GL}_{n_1}(\mathcal {O}_F)$. By choosing a basis
$U=\mathrm {GL}_{n_1}(\mathcal {O}_F)$. By choosing a basis ![]() $\{l_1,\ldots,l_{n_1}\}$ of
$\{l_1,\ldots,l_{n_1}\}$ of ![]() $L_1$, we may identify
$L_1$, we may identify ![]() $U\backslash G$ with
$U\backslash G$ with ![]() $\{L_1'\mid L_1\subset L_1'\subset L_{1,F}\}$ by sending
$\{L_1'\mid L_1\subset L_1'\subset L_{1,F}\}$ by sending ![]() $g$ to
$g$ to ![]() $L_1\cdot g^{-1}$. Then the identity we want to prove is equivalent to
$L_1\cdot g^{-1}$. Then the identity we want to prove is equivalent to
where ![]() $|\pi |=q^{-1}.$ By a partition of
$|\pi |=q^{-1}.$ By a partition of ![]() $M^n_{k}$, we have
$M^n_{k}$, we have
 \begin{align*} \alpha(M,L,X)&=\int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^n} \psi(\langle Y,T({\bf x})-T\rangle) \,d{\bf x}\\ &= \sum_{g\in U\backslash G } \int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^{n,(n_1)}\cdot g_1} \psi(\langle Y,T({\bf x})-T\rangle) \,d{\bf x}, \end{align*}
\begin{align*} \alpha(M,L,X)&=\int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^n} \psi(\langle Y,T({\bf x})-T\rangle) \,d{\bf x}\\ &= \sum_{g\in U\backslash G } \int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^{n,(n_1)}\cdot g_1} \psi(\langle Y,T({\bf x})-T\rangle) \,d{\bf x}, \end{align*}
where ![]() $g_1=\mathrm {Diag}(g, I_{n-n_1})$, and the action of
$g_1=\mathrm {Diag}(g, I_{n-n_1})$, and the action of ![]() $g_1$ is simply matrix multiplication on the
$g_1$ is simply matrix multiplication on the ![]() $n$ components of
$n$ components of ![]() $M^{n,(n_1)}$. Now
$M^{n,(n_1)}$. Now
 \begin{align*}
&\int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}\cdot g_1} \psi(\langle Y,T({\bf
x})-T\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m}
\int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^{n,(n_1)}}
\psi(\langle Y,T({\bf x} g_1)-T\rangle) \,d{\bf x}\\
&\qquad= |{\det g_1}|^{2k+m} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y,(T({\bf
x})-T[g_1^{-1}])[g_1]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y[g_1^*],T({\bf
x})-T[g_1^{-1}]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m-n} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y,T({\bf
x})-T[g_1^{-1}]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m-n} \beta(M^{[k]},L\cdot g_1^{-1})^{(n_1)}.
\end{align*}
\begin{align*}
&\int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}\cdot g_1} \psi(\langle Y,T({\bf
x})-T\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m}
\int_{\mathrm{Herm}_n(F)} \,dY \int_{(M^{[k]})^{n,(n_1)}}
\psi(\langle Y,T({\bf x} g_1)-T\rangle) \,d{\bf x}\\
&\qquad= |{\det g_1}|^{2k+m} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y,(T({\bf
x})-T[g_1^{-1}])[g_1]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y[g_1^*],T({\bf
x})-T[g_1^{-1}]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m-n} \int_{\mathrm{Herm}_n(F)} \,dY
\int_{(M^{[k]})^{n,(n_1)}} \psi(\langle Y,T({\bf
x})-T[g_1^{-1}]\rangle) \,d{\bf x}\\ &\qquad= |{\det g_1}|^{2k+m-n} \beta(M^{[k]},L\cdot g_1^{-1})^{(n_1)}.
\end{align*}
Here ![]() $T[g]:= g^{*}Tg$. Now the lemma is clear.
$T[g]:= g^{*}Tg$. Now the lemma is clear.
Theorem 5.2 Let ![]() $L$ be as in Lemma 5.1. Then
$L$ be as in Lemma 5.1. Then
 \[ \alpha(M, L, X) = \sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2+i(n-m)}X^{i} \cdot \sum_{\substack{L_1 \subset L_1' \subset \pi^{-1}L_{1} \\ \dim {L_1'/L_1}=i}} \alpha(M, L_1'\oplus L_2,X) + \beta(M, L,X)^{(n_1)}. \]
\[ \alpha(M, L, X) = \sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2+i(n-m)}X^{i} \cdot \sum_{\substack{L_1 \subset L_1' \subset \pi^{-1}L_{1} \\ \dim {L_1'/L_1}=i}} \alpha(M, L_1'\oplus L_2,X) + \beta(M, L,X)^{(n_1)}. \]
Proof. This is an analogue of [Reference KatsuradaKat99, Proposition 2.1]. The proof follows from a combination of the argument (in a reverse order) in Lemmas 2.16 and 5.1.
Motivated by Theorem 5.2, we give the following definition.
Definition 5.3 Let ![]() $L =L_1 \oplus L_2$ be as in Lemma 5.1. We define
$L =L_1 \oplus L_2$ be as in Lemma 5.1. We define
 \begin{equation} \partial \mathrm{Den}(L)^{(n_1)}:= \partial \mathrm{Den}(L)-\sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2} \sum_{\substack{L_1 \subset L_1' \subset L_{1, F} \\ \dim {L_1'/L_1}=i}} \partial \mathrm{Den}(L'_1\oplus L_2). \end{equation}
\begin{equation} \partial \mathrm{Den}(L)^{(n_1)}:= \partial \mathrm{Den}(L)-\sum_{i=1}^{n_1} (-1)^{i-1} q^{i(i-1)/2} \sum_{\substack{L_1 \subset L_1' \subset L_{1, F} \\ \dim {L_1'/L_1}=i}} \partial \mathrm{Den}(L'_1\oplus L_2). \end{equation}Corollary 5.4 Let ![]() $L =L_1 \oplus L_2$ be as in Lemma 5.1, and
$L =L_1 \oplus L_2$ be as in Lemma 5.1, and ![]() $\epsilon =\chi (L)$. Then
$\epsilon =\chi (L)$. Then
 \[ \partial
\mathrm{Den}(L)^{(n_1)}=\frac{1}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon})}
\biggl(2\beta'(I_{n}^{-\epsilon},L)^{(n_1)}+\sum_{i}c^{n,i}_{\epsilon}\beta(\mathcal{H}_{n,i}^{\epsilon},L)^{(n_1)}\biggr).
\]
\[ \partial
\mathrm{Den}(L)^{(n_1)}=\frac{1}{\alpha(I_{n}^{-\epsilon},I_{n}^{-\epsilon})}
\biggl(2\beta'(I_{n}^{-\epsilon},L)^{(n_1)}+\sum_{i}c^{n,i}_{\epsilon}\beta(\mathcal{H}_{n,i}^{\epsilon},L)^{(n_1)}\biggr).
\]
As a corollary of Lemma 5.1, we have the following.
Corollary 5.5 Let ![]() $L =L_1 \oplus L_2$ be as in Lemma 5.1. Then we have the following identity where the summation is finite:
$L =L_1 \oplus L_2$ be as in Lemma 5.1. Then we have the following identity where the summation is finite:
We may reduce the identity ![]() $\mathrm {Int}(L)=\partial \mathrm {Den}(L)$ to a primitive version as the following theorem shows.
$\mathrm {Int}(L)=\partial \mathrm {Den}(L)$ to a primitive version as the following theorem shows.
Theorem 5.6 Let ![]() $L=L_1 \oplus L_2 \subset \mathbb {V}$ be as in Lemma 5.1.
$L=L_1 \oplus L_2 \subset \mathbb {V}$ be as in Lemma 5.1.
(1) Conjecture 1.1 is true for
 $L$ if for every
$L$ if for every  $L_1 \subset L_1' \subset L_{1, F}$, we have
$L_1 \subset L_1' \subset L_{1, F}$, we have
 \[ \mathrm{Int}(L_1' \oplus L_2)^{(n_1)}= \partial \mathrm{Den}(L_1' \oplus L_2)^{(n_1)}. \]
\[ \mathrm{Int}(L_1' \oplus L_2)^{(n_1)}= \partial \mathrm{Den}(L_1' \oplus L_2)^{(n_1)}. \]
(2) If Conjecture 1.1 holds for all lattices
 $L'=L_1'\oplus L_2$ of
$L'=L_1'\oplus L_2$ of  $\mathbb {V}$ of rank
$\mathbb {V}$ of rank  $n$ with
$n$ with  $L_1 \subset L_1' \subset L_{1, F}$, then
$L_1 \subset L_1' \subset L_{1, F}$, then
 \[ \mathrm{Int}(L_1 \oplus L_2)^{(n_1)} =\partial \mathrm{Den}(L_1 \oplus L_2)^{(n_1)}. \]
\[ \mathrm{Int}(L_1 \oplus L_2)^{(n_1)} =\partial \mathrm{Den}(L_1 \oplus L_2)^{(n_1)}. \]
(3) For
 $1 \le n_1 \le n$, Conjecture 1.1 is true if and only if for every lattice
$1 \le n_1 \le n$, Conjecture 1.1 is true if and only if for every lattice  $L =L_1 \oplus L_2 \subset \mathbb {V}$ with
$L =L_1 \oplus L_2 \subset \mathbb {V}$ with  $\mathrm {rank}(L_1)=n_1$, one has
$\mathrm {rank}(L_1)=n_1$, one has
 \[ \mathrm{Int}(L_1 \oplus L_2)^{(n_1)} =\partial \mathrm{Den}(L_1 \oplus L_2)^{(n_1)}. \]
\[ \mathrm{Int}(L_1 \oplus L_2)^{(n_1)} =\partial \mathrm{Den}(L_1 \oplus L_2)^{(n_1)}. \]
Proof. Part (1) follows from Lemma 2.16 and Corollary 5.5. Part (2) follows from Definitions 2.15 and 5.3. Part (3) follows from parts (1) and (2).
For the rest of this section, we assume that ![]() $M$ is unimodular of rank
$M$ is unimodular of rank ![]() $m$ with a Gram matrix
$m$ with a Gram matrix ![]() $\mathrm {Diag}(I_{m-1}, \nu )$. To go further with the calculation of
$\mathrm {Diag}(I_{m-1}, \nu )$. To go further with the calculation of ![]() $\alpha (M,L,X)$, we need an induction formula for
$\alpha (M,L,X)$, we need an induction formula for ![]() $\beta (M,L,X)^{(\ell )}$ as follows. The proof is essentially the same as that of Corollary 9.11 of [Reference Kudla and RapoportKR11], and is left to the reader.
$\beta (M,L,X)^{(\ell )}$ as follows. The proof is essentially the same as that of Corollary 9.11 of [Reference Kudla and RapoportKR11], and is left to the reader.
Proposition 5.7 Let ![]() $L=L_1 {\unicode{x29BA}} L_2$, where
$L=L_1 {\unicode{x29BA}} L_2$, where ![]() $L_j$ is of rank
$L_j$ is of rank ![]() $n_j$. Let
$n_j$. Let ![]() $C(M^{[k]}, L_1)$ be the
$C(M^{[k]}, L_1)$ be the ![]() $\mathrm {U}(M^{[k]})$-orbits of sublattices
$\mathrm {U}(M^{[k]})$-orbits of sublattices ![]() $M(i) \subset M^{[k]}$ such that
$M(i) \subset M^{[k]}$ such that ![]() $M(i)$ is isometric to
$M(i)$ is isometric to ![]() $L_1$, and write
$L_1$, and write ![]() $C(M^{[k]}, L_1)=\sqcup _{i\in J}\{ M(i) \}$. Then
$C(M^{[k]}, L_1)=\sqcup _{i\in J}\{ M(i) \}$. Then
where
 \begin{align*} &\beta_i(M, L_1, X)\\ &\quad=\lim_{d\to
\infty}q^{-d n_1 (2m+4k -n_1)} \#\big\{ \phi \in I(M^{[k]},
L_1,d)^{(n_1)} \mid \exists\, \ \Phi \in \mathrm{U}(M)
\text{ with } \phi(L_1)=\Phi(M(i))\big\}, \end{align*}
\begin{align*} &\beta_i(M, L_1, X)\\ &\quad=\lim_{d\to
\infty}q^{-d n_1 (2m+4k -n_1)} \#\big\{ \phi \in I(M^{[k]},
L_1,d)^{(n_1)} \mid \exists\, \ \Phi \in \mathrm{U}(M)
\text{ with } \phi(L_1)=\Phi(M(i))\big\}, \end{align*}
and
Recall that ![]() $I(M^{[k]},L_1,d)$ is defined in (5.3).
$I(M^{[k]},L_1,d)$ is defined in (5.3).
One special case is that ![]() $L=\mathcal {H}^i{\unicode{x29BA}} L_2$. Since any sublattice of
$L=\mathcal {H}^i{\unicode{x29BA}} L_2$. Since any sublattice of ![]() $M^{[k]}=M{\unicode{x29BA}} \mathcal {H}^k$ isometric to
$M^{[k]}=M{\unicode{x29BA}} \mathcal {H}^k$ isometric to ![]() $\mathcal {H}^i$ is always a direct summand of
$\mathcal {H}^i$ is always a direct summand of ![]() $M^{[k]}$ and
$M^{[k]}$ and ![]() $\alpha (M,\mathcal {H}^i,X)=\beta (M,\mathcal {H}^i,X)^{(2i)}=\beta (M,\mathcal {H}^i,X)$, the above proposition specializes as follows.
$\alpha (M,\mathcal {H}^i,X)=\beta (M,\mathcal {H}^i,X)^{(2i)}=\beta (M,\mathcal {H}^i,X)$, the above proposition specializes as follows.
Corollary 5.8 Assume ![]() $L=\mathcal {H}^i{\unicode{x29BA}} L_2$, then
$L=\mathcal {H}^i{\unicode{x29BA}} L_2$, then
We end this section with two more special cases of Proposition 5.7. Proofs are given in Appendix A.
Proposition 5.9 Let the notation be as in Proposition 5.7. Assume ![]() $n_1=1$ and
$n_1=1$ and ![]() $L_1 =\langle t \rangle$ where
$L_1 =\langle t \rangle$ where ![]() $t\in \mathcal {O}_{F_0}.$
$t\in \mathcal {O}_{F_0}.$
(1) There always exists a primitive vector
 $M(1)\in \mathcal {H}^k$ with
$M(1)\in \mathcal {H}^k$ with  $q(M(1))=t$, and
Here
$q(M(1))=t$, and
Here \[ M(1)^{\perp} \cong \mathcal{H}^{k-1} {\unicode{x29BA}} I_{m}^{\chi(M)} {\unicode{x29BA}} \langle -t \rangle. \]
\[ M(1)^{\perp} \cong \mathcal{H}^{k-1} {\unicode{x29BA}} I_{m}^{\chi(M)} {\unicode{x29BA}} \langle -t \rangle. \]
 $\langle t \rangle$ denotes a lattice
$\langle t \rangle$ denotes a lattice  $\mathcal {O}_F v$ of rank one with
$\mathcal {O}_F v$ of rank one with  $(v, v)=t$.
$(v, v)=t$.(2) If
 $\mathrm {v}(t)=0$, then there exist a primitive vector
$\mathrm {v}(t)=0$, then there exist a primitive vector  $M(0)\in M$ with
$M(0)\in M$ with  $q(M(0))=t$, and
Here
$q(M(0))=t$, and
Here \[ M(0)^{\perp}\cong \mathcal{H}^{k}{\unicode{x29BA}} I_{m-2}^{\epsilon_{m-2}} {\unicode{x29BA}} \langle \nu t \rangle. \]
\[ M(0)^{\perp}\cong \mathcal{H}^{k}{\unicode{x29BA}} I_{m-2}^{\epsilon_{m-2}} {\unicode{x29BA}} \langle \nu t \rangle. \]
 $\epsilon _{m-2}=\chi ((-1)^{(m-2)(m-3)/2})$.
$\epsilon _{m-2}=\chi ((-1)^{(m-2)(m-3)/2})$.(3) If
 $\mathrm {v}(t)>0$, then there exist a primitive vector
$\mathrm {v}(t)>0$, then there exist a primitive vector  $M(0)\in M$ with
$M(0)\in M$ with  $q(M(0))=t$ only when
$q(M(0))=t$ only when  $M$ is isotropic (i.e.
$M$ is isotropic (i.e.  $\exists \, v\in M$ with
$\exists \, v\in M$ with  $q(v)=0$). In this case,
Assuming the existence of
$q(v)=0$). In this case,
Assuming the existence of \[ M(0)^{\perp}\cong \mathcal{H}^{k}{\unicode{x29BA}} I_{m-2}^{\chi(M)} {\unicode{x29BA}} \langle -t \rangle. \]
\[ M(0)^{\perp}\cong \mathcal{H}^{k}{\unicode{x29BA}} I_{m-2}^{\chi(M)} {\unicode{x29BA}} \langle -t \rangle. \]
 $M(1)$ and
$M(1)$ and  $M(0)$, we have
$M(0)$, we have
 \[ |M^{[k]}:M(i){\unicode{x29BA}} M(i)^{\perp}|^{-1}|M(i)^{\vee}:M(i)|=\begin{cases} 1, & \text{if }i=1,\\ q, & \text{if }i=0. \end{cases} \]
\[ |M^{[k]}:M(i){\unicode{x29BA}} M(i)^{\perp}|^{-1}|M(i)^{\vee}:M(i)|=\begin{cases} 1, & \text{if }i=1,\\ q, & \text{if }i=0. \end{cases} \]
(4) Under the action of
 $\mathrm {U}(M^{[k]})$,
$\mathrm {U}(M^{[k]})$,  $v$ is either in the same orbit of a fixed vector
$v$ is either in the same orbit of a fixed vector  $M(1)\in \mathcal {H}^k$ or a fixed vector
$M(1)\in \mathcal {H}^k$ or a fixed vector  $M(0)\in M$.
$M(0)\in M$.(5) We have the following induction formula:
Moreover: \[ \beta(M, L,X)^{(1)} =\beta_1(M,L_1,X) \alpha(M(1)^{\perp},L_2)+q^{n-1}\beta_0(M, L_1,X) \alpha(M(0)^{\perp},L_2). \]
\[ \beta(M, L,X)^{(1)} =\beta_1(M,L_1,X) \alpha(M(1)^{\perp},L_2)+q^{n-1}\beta_0(M, L_1,X) \alpha(M(0)^{\perp},L_2). \]
(a) for any
 $L_1$,
$L_1$,
 \begin{align*} \beta_1(M, L_1,X)=1-X; \end{align*}
\begin{align*} \beta_1(M, L_1,X)=1-X; \end{align*}
(b) assume
 $\mathrm {v}(t)=0$, then
$\mathrm {v}(t)=0$, then
 \[ \beta_0(M, L_1 ,X)=\begin{cases}
\big(1+\chi(M) \chi(L)q^{-({m-1})/{2}})X, & \text{if
}m\text{ is odd},\\ \big(1-\chi(M)q^{-{m}/{2}})X, &
\text{if }m\text{ is even}; \end{cases}
\]
\[ \beta_0(M, L_1 ,X)=\begin{cases}
\big(1+\chi(M) \chi(L)q^{-({m-1})/{2}})X, & \text{if
}m\text{ is odd},\\ \big(1-\chi(M)q^{-{m}/{2}})X, &
\text{if }m\text{ is even}; \end{cases}
\]
(c) assume
 $\mathrm {v}(t)>0$, then
$\mathrm {v}(t)>0$, then
 \[ \beta_0(M, L_1 ,X)=\begin{cases}
\big(1-q^{1-m}\big)X, & \text{if }m\text{ is odd},\\
\big(1-q^{1-m}+\chi(M)(q-1)q^{-{m}/{2}}\big)X, & \text{if
}m\text{ is even}. \end{cases} \]
\[ \beta_0(M, L_1 ,X)=\begin{cases}
\big(1-q^{1-m}\big)X, & \text{if }m\text{ is odd},\\
\big(1-q^{1-m}+\chi(M)(q-1)q^{-{m}/{2}}\big)X, & \text{if
}m\text{ is even}. \end{cases} \]
Proof. Parts (1)–(4) are proved in § A.1. The induction formula for ![]() $\beta (M, L,X)^{(1)}$ follows from Proposition 5.7. For the formula of
$\beta (M, L,X)^{(1)}$ follows from Proposition 5.7. For the formula of ![]() $\beta _i(M, L_1 ,X)$, see Corollaries A.10 and A.12.
$\beta _i(M, L_1 ,X)$, see Corollaries A.10 and A.12.
Proposition 5.10 Let the notation be as in Proposition 5.7. Assume ![]() $\mathrm {v}(L_1)>0$ and
$\mathrm {v}(L_1)>0$ and ![]() ${n_1=2}$. Then we have a partition of
${n_1=2}$. Then we have a partition of ![]() $C(M^{[k]}, L_1)=\bigsqcup _{i=0}^{2}C_i(M^{[k]},L_1)$ such that for any
$C(M^{[k]}, L_1)=\bigsqcup _{i=0}^{2}C_i(M^{[k]},L_1)$ such that for any ![]() $M(i)\in C_i(M^{[k]},L_1)$,
$M(i)\in C_i(M^{[k]},L_1)$, ![]() $M(i)^{\bot }$ is isometric to
$M(i)^{\bot }$ is isometric to
Here ![]() $M^{(i)}$ is a unimodular
$M^{(i)}$ is a unimodular ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $m-2(2-i)$ and has determinant
$m-2(2-i)$ and has determinant ![]() $(-1)^i \det L$.
$(-1)^i \det L$.
Moreover, we have
 \begin{equation} \beta(M, L,X)^{(2)}=\sum_{i=0}^{2}q^{(2-i)(n-2)}\beta_i(M,L_1,X)\alpha(M(i)^{\perp}, L_2,X), \end{equation}
\begin{equation} \beta(M, L,X)^{(2)}=\sum_{i=0}^{2}q^{(2-i)(n-2)}\beta_i(M,L_1,X)\alpha(M(i)^{\perp}, L_2,X), \end{equation}where
 \begin{align*}
\beta_2(M,L_1,X)&=(1-X)(1-q^2 X),\\
\beta_1(M,L_1,X)&= q(q+1)\big( (1-q^{1-m})+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}\big)X(1-X),\\
\beta_0(M,L_1,X) &=\begin{cases}
q(1-q^{1-m})(1-q^{3-m})X^2, & \text{if }m\text{ is odd},\\
q\big( (1-q^{2-m})+\chi(M)(q^2-1)q^{-{m}/{2}}\big)(1-q^{2-m})X^2, & \text{if }m\text{ is even}. \end{cases}
\end{align*}
\begin{align*}
\beta_2(M,L_1,X)&=(1-X)(1-q^2 X),\\
\beta_1(M,L_1,X)&= q(q+1)\big( (1-q^{1-m})+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}\big)X(1-X),\\
\beta_0(M,L_1,X) &=\begin{cases}
q(1-q^{1-m})(1-q^{3-m})X^2, & \text{if }m\text{ is odd},\\
q\big( (1-q^{2-m})+\chi(M)(q^2-1)q^{-{m}/{2}}\big)(1-q^{2-m})X^2, & \text{if }m\text{ is even}. \end{cases}
\end{align*}
Here ![]() $\delta _e(m)=1$ or
$\delta _e(m)=1$ or ![]() $0$ depending on whether
$0$ depending on whether ![]() $m$ is even or odd.
$m$ is even or odd.
6. The modified Kudla–Rapoport conjecture
Recall that the Hermitian lattices used to define the correction terms are of the following forms:
where ![]() $I_{n-2i}^{\epsilon }$ is the unimodular Hermitian lattice of rank
$I_{n-2i}^{\epsilon }$ is the unimodular Hermitian lattice of rank ![]() $n-2i$ with
$n-2i$ with ![]() $\chi (I_{n-2i}^{\epsilon })= \chi (\mathcal {H}_{n,i}^{\epsilon } )=\epsilon$. When
$\chi (I_{n-2i}^{\epsilon })= \chi (\mathcal {H}_{n,i}^{\epsilon } )=\epsilon$. When ![]() $n=2r$ is even, we take
$n=2r$ is even, we take ![]() $I_{0}^{\epsilon } =0$ and
$I_{0}^{\epsilon } =0$ and ![]() $\mathcal {H}_{n, r}^1 = \mathcal {H}^{r}$.
$\mathcal {H}_{n, r}^1 = \mathcal {H}^{r}$.
Theorem 6.1 Let ![]() $r_\epsilon =({n-1})/2$ when
$r_\epsilon =({n-1})/2$ when ![]() $n$ is odd, and
$n$ is odd, and ![]() $r_\epsilon =\lfloor ({n+\epsilon })/2\rfloor$ when
$r_\epsilon =\lfloor ({n+\epsilon })/2\rfloor$ when ![]() $n$ is even. In the following, we just write
$n$ is even. In the following, we just write ![]() $r_{\epsilon }$ as
$r_{\epsilon }$ as ![]() $r$:
$r$:
 \begin{align*} A^\epsilon =(A_{i, j}^\epsilon) &= \begin{pmatrix} \alpha(\mathcal{H}_{n,1}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) & \alpha(\mathcal{H}_{n,2}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) & \cdots & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) \\ 0 & \alpha(\mathcal{H}_{n,2}^{\epsilon}, \mathcal{H}_{n,2}^{\epsilon}) & \cdots & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,2}^{\epsilon}) \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,r}^{\epsilon}) \end{pmatrix},\\ B^\epsilon &= {}^t(\alpha'(I_{n}^{-\epsilon}, \mathcal{H}_{\epsilon}^{n, 1}), \ldots, \alpha'(I_{n}^{-\epsilon}, \mathcal{H}_{n,r}^{\epsilon})), \end{align*}
\begin{align*} A^\epsilon =(A_{i, j}^\epsilon) &= \begin{pmatrix} \alpha(\mathcal{H}_{n,1}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) & \alpha(\mathcal{H}_{n,2}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) & \cdots & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,1}^{\epsilon}) \\ 0 & \alpha(\mathcal{H}_{n,2}^{\epsilon}, \mathcal{H}_{n,2}^{\epsilon}) & \cdots & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,2}^{\epsilon}) \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \alpha(\mathcal{H}_{n,r}^{\epsilon}, \mathcal{H}_{n,r}^{\epsilon}) \end{pmatrix},\\ B^\epsilon &= {}^t(\alpha'(I_{n}^{-\epsilon}, \mathcal{H}_{\epsilon}^{n, 1}), \ldots, \alpha'(I_{n}^{-\epsilon}, \mathcal{H}_{n,r}^{\epsilon})), \end{align*}
and
where ![]() $c_{n,i}^\epsilon$ is as in Conjecture 1.1.
$c_{n,i}^\epsilon$ is as in Conjecture 1.1.
Then ![]() $C^\epsilon$ is the solution of the equation
$C^\epsilon$ is the solution of the equation
Moreover,
 \begin{align}
A_{j,j}^\epsilon&=2q^{{(n-2j)(n-2j-1)}/{2}} \prod_{0<
s\le j}(1-q^{-2s})\prod_{1 \le s \le
\lfloor({n-2j-1})/{2}\rfloor}(1-q^{-2s})\nonumber\\ &\quad
\times \begin{cases} 1, & \text{if }n\text{ is odd},\\
1, -\epsilon q^{-({n-2j})/{2}}, & \text{if }n\text{ is
even}. \end{cases} \end{align}
\begin{align}
A_{j,j}^\epsilon&=2q^{{(n-2j)(n-2j-1)}/{2}} \prod_{0<
s\le j}(1-q^{-2s})\prod_{1 \le s \le
\lfloor({n-2j-1})/{2}\rfloor}(1-q^{-2s})\nonumber\\ &\quad
\times \begin{cases} 1, & \text{if }n\text{ is odd},\\
1, -\epsilon q^{-({n-2j})/{2}}, & \text{if }n\text{ is
even}. \end{cases} \end{align}
Finally, for ![]() $i< j$,
$i< j$,
 \begin{equation} A_{i,j}^\epsilon=
A_{j,j}^\epsilon\cdot \begin{cases}
I\left(n-2i,\dfrac{n-2i-1}{2},j-i\right), & \text{if
}n\text{ is odd},\\
I\left(n-2i,\dfrac{n-2i-1+\epsilon}{2},j-i\right), &
\text{if }n\text{ is even}, \end{cases}
\end{equation}
\begin{equation} A_{i,j}^\epsilon=
A_{j,j}^\epsilon\cdot \begin{cases}
I\left(n-2i,\dfrac{n-2i-1}{2},j-i\right), & \text{if
}n\text{ is odd},\\
I\left(n-2i,\dfrac{n-2i-1+\epsilon}{2},j-i\right), &
\text{if }n\text{ is even}, \end{cases}
\end{equation}
where
 \[ I(n,d,k):= \prod_{s=1}^{k}\frac{(q^{d-s+1}-1)(q^{n-d-s}+1)}{q^s-1}. \]
\[ I(n,d,k):= \prod_{s=1}^{k}\frac{(q^{d-s+1}-1)(q^{n-d-s}+1)}{q^s-1}. \]
Proof. First note that ![]() $\alpha (\mathcal {H}_{n, i}^\epsilon, \mathcal {H}_{n,j}^{\epsilon })=0$ if
$\alpha (\mathcal {H}_{n, i}^\epsilon, \mathcal {H}_{n,j}^{\epsilon })=0$ if ![]() $i< j$. Thus, (1.9) is indeed equivalent to (6.2), and there exists a unique solution
$i< j$. Thus, (1.9) is indeed equivalent to (6.2), and there exists a unique solution ![]() $C_{\epsilon }$.
$C_{\epsilon }$.
Now we compute ![]() $A_{j,j}^\epsilon$ explicitly. Corollary 5.8 and Lemma A.9 imply that
$A_{j,j}^\epsilon$ explicitly. Corollary 5.8 and Lemma A.9 imply that
According to Lemma A.8,
By Lemma A.11,
where ![]() $\overline {I}_{n-2j}^{\epsilon }=I_{n-2j}^\epsilon \otimes _{\mathcal {O}_F} \mathcal {O}_{F}/(\pi )$ is the space over
$\overline {I}_{n-2j}^{\epsilon }=I_{n-2j}^\epsilon \otimes _{\mathcal {O}_F} \mathcal {O}_{F}/(\pi )$ is the space over ![]() $\mathbb {F}_q$ with the naturally induced quadratic form. Now (6.3) follows from the well-known formula:
$\mathbb {F}_q$ with the naturally induced quadratic form. Now (6.3) follows from the well-known formula:
 \[
|\mathrm{O}(\overline{I}_{n-2j}^{\epsilon})(\mathbb{F}_q)|
=\begin{cases}
2q^{{(n-2j)(n-2j-1)}/{2}}\displaystyle\prod _{s=1}^{({n-2j-1})/{2}}(1-q^{-2s}), & \text{if }n\text{ is odd},\\
2q^{{(n-2j)(n-2j-1)}/{2}}(1-\epsilon q^{-({n-2j})/{2}})\displaystyle\prod _{s=1}^{(({n-2j})/{2})-1}(1-q^{-2s}), & \text{if }n\text{
is even}. \end{cases} \]
\[
|\mathrm{O}(\overline{I}_{n-2j}^{\epsilon})(\mathbb{F}_q)|
=\begin{cases}
2q^{{(n-2j)(n-2j-1)}/{2}}\displaystyle\prod _{s=1}^{({n-2j-1})/{2}}(1-q^{-2s}), & \text{if }n\text{ is odd},\\
2q^{{(n-2j)(n-2j-1)}/{2}}(1-\epsilon q^{-({n-2j})/{2}})\displaystyle\prod _{s=1}^{(({n-2j})/{2})-1}(1-q^{-2s}), & \text{if }n\text{
is even}. \end{cases} \]
To obtain (6.4), note that (Corollary 5.8)
and
Hence,
 \[ \frac{A_{i, j}^\epsilon}{A_{j, j}^\epsilon}= \frac{\alpha(\mathcal{H}_{n,j}^{\epsilon},\mathcal{H}_{n,i}^{\epsilon})}{\alpha(\mathcal{H}_{n,j}^{\epsilon},\mathcal{H}_{n,j}^{\epsilon})}=\frac{\alpha(\mathcal{H}_{n-2i,j-i}^{\epsilon},I_{n-2i}^{\epsilon})}{\alpha(\mathcal{H}_{n-2i,j-i}^{\epsilon},\mathcal{H}_{n-2i,j-i}^{\epsilon})}. \]
\[ \frac{A_{i, j}^\epsilon}{A_{j, j}^\epsilon}= \frac{\alpha(\mathcal{H}_{n,j}^{\epsilon},\mathcal{H}_{n,i}^{\epsilon})}{\alpha(\mathcal{H}_{n,j}^{\epsilon},\mathcal{H}_{n,j}^{\epsilon})}=\frac{\alpha(\mathcal{H}_{n-2i,j-i}^{\epsilon},I_{n-2i}^{\epsilon})}{\alpha(\mathcal{H}_{n-2i,j-i}^{\epsilon},\mathcal{H}_{n-2i,j-i}^{\epsilon})}. \]
Fix an ![]() $\mathcal {O}_F$-lattice
$\mathcal {O}_F$-lattice ![]() $L$ that is represented by
$L$ that is represented by ![]() $I_{n-2i}^{\epsilon }$. According to Lemma 6.2, to compute
$I_{n-2i}^{\epsilon }$. According to Lemma 6.2, to compute ![]() ${A_{i, j}^\epsilon }/{A_{j, j}^\epsilon }$, we need to count the number of lattices
${A_{i, j}^\epsilon }/{A_{j, j}^\epsilon }$, we need to count the number of lattices ![]() $L'$ in
$L'$ in ![]() $L_{F}$ such that contain
$L_{F}$ such that contain ![]() $L\subset L'$ and
$L\subset L'$ and ![]() $L' \cong \mathcal {H}_{n-2i,j-i}^{\epsilon }$, which is equivalent to the following condition:
$L' \cong \mathcal {H}_{n-2i,j-i}^{\epsilon }$, which is equivalent to the following condition:
Since ![]() $L'$ and
$L'$ and ![]() $\pi L'$ determine each other, we just need to count
$\pi L'$ determine each other, we just need to count ![]() $\pi L'$ satisfying the above condition. We regard
$\pi L'$ satisfying the above condition. We regard ![]() $\pi L'/\pi L$ as a
$\pi L'/\pi L$ as a ![]() $(j-i)$-dimensional subspace of
$(j-i)$-dimensional subspace of ![]() $L/\pi L$, where
$L/\pi L$, where ![]() $L/\pi L$ is equipped with quadratic form
$L/\pi L$ is equipped with quadratic form ![]() $(x,y)/\pi$.
$(x,y)/\pi$.
Claim The condition
is equivalent to the condition that ![]() $\pi L'/\pi L$ is an isotropic subspace of
$\pi L'/\pi L$ is an isotropic subspace of ![]() $L/\pi L.$
$L/\pi L.$
Indeed, assume ![]() $\pi L'/\pi L$ is an isotropic subspace of
$\pi L'/\pi L$ is an isotropic subspace of ![]() $L/\pi L.$ Then
$L/\pi L.$ Then ![]() $(\pi x, \pi y)\in \pi \mathcal {O}_F$ for any
$(\pi x, \pi y)\in \pi \mathcal {O}_F$ for any ![]() $x,y\in L'$, which is equivalent to
$x,y\in L'$, which is equivalent to ![]() $(x,\pi y)\in \mathcal {O}_F$ for any
$(x,\pi y)\in \mathcal {O}_F$ for any ![]() $x,y\in L'$. The latter condition is the same as
$x,y\in L'$. The latter condition is the same as ![]() $L' \stackrel {}{\subset } (L')^\sharp$. The other direction is clear.
$L' \stackrel {}{\subset } (L')^\sharp$. The other direction is clear.
Therefore, ![]() ${A_{i, j}^\epsilon }/{A_{j, j}^\epsilon }$ is the number of
${A_{i, j}^\epsilon }/{A_{j, j}^\epsilon }$ is the number of ![]() $(j-i)$-dimensional isotropic subspaces of
$(j-i)$-dimensional isotropic subspaces of ![]() $L/\pi L$. According to [Reference Li and ZhangLZ22b, Lemma 3.2.2], it equals to
$L/\pi L$. According to [Reference Li and ZhangLZ22b, Lemma 3.2.2], it equals to
 \[ \begin{cases}
I\left(n-2i,\dfrac{n-2i-1}{2},j-i\right)\!, & \text{if
}n\text{ is odd},\\
I\left(n-2i,\dfrac{n-2i-1+\epsilon}{2},j-i\right)\!, &
\text{if }n\text{ is even}. \end{cases}
\]
\[ \begin{cases}
I\left(n-2i,\dfrac{n-2i-1}{2},j-i\right)\!, & \text{if
}n\text{ is odd},\\
I\left(n-2i,\dfrac{n-2i-1+\epsilon}{2},j-i\right)\!, &
\text{if }n\text{ is even}. \end{cases}
\]
□
According to Theorem 6.1, in order to solve ![]() $C^\epsilon$, we need to know
$C^\epsilon$, we need to know ![]() $B^\epsilon$ and
$B^\epsilon$ and ![]() $A^\epsilon$. Here,
$A^\epsilon$. Here, ![]() $B^\epsilon$ can be calculated by applying Corollary 5.8 and Proposition 5.9 inductively. The following lemma can be used to compute
$B^\epsilon$ can be calculated by applying Corollary 5.8 and Proposition 5.9 inductively. The following lemma can be used to compute ![]() $A^\epsilon$.
$A^\epsilon$.
Lemma 6.2 Let ![]() $F/F_0$ be a quadratic
$F/F_0$ be a quadratic ![]() $p$-adic field extension, and let
$p$-adic field extension, and let ![]() $L$ and
$L$ and ![]() $M$ be two
$M$ be two ![]() $\mathcal {O}_F$-Hermitian lattices of rank
$\mathcal {O}_F$-Hermitian lattices of rank ![]() $n$. Then
$n$. Then ![]() ${\alpha (M, L)}/{\alpha (M, M)}$ is equal to the number of lattices
${\alpha (M, L)}/{\alpha (M, M)}$ is equal to the number of lattices ![]() $L'$ in
$L'$ in ![]() $L_F$ containing
$L_F$ containing ![]() $L$ and isometric to
$L$ and isometric to ![]() $M$.
$M$.
Proof. The proof is a generalization of that of Proposition 10.2 of [Reference Kudla and RapoportKR14b] and works for both inert and ramified primes.
Let us assume that there is an isometric embedding from ![]() $L$ into
$L$ into ![]() $M$, otherwise both sides of the identity in the lemma are zero. In this case, we have a fixed
$M$, otherwise both sides of the identity in the lemma are zero. In this case, we have a fixed ![]() $L_F \cong M_F$. Let
$L_F \cong M_F$. Let ![]() $\alpha$ (respectively,
$\alpha$ (respectively, ![]() $\beta$) be a top degree translation invariant form on
$\beta$) be a top degree translation invariant form on ![]() $L_F^n$ (respectively,
$L_F^n$ (respectively, ![]() $\mathrm {Herm}_n(F)$). Let
$\mathrm {Herm}_n(F)$). Let ![]() $\nu _p=\alpha /h^*(\beta )$ where
$\nu _p=\alpha /h^*(\beta )$ where
Define ![]() $X$ to be the set of
$X$ to be the set of ![]() $F$-linear isometric embeddings from
$F$-linear isometric embeddings from ![]() $L$ into
$L$ into ![]() $M$. By fixing a basis of
$M$. By fixing a basis of ![]() $L_F$ and regarding
$L_F$ and regarding ![]() $\phi \in X$ as a linear isometry from
$\phi \in X$ as a linear isometry from ![]() $L_F$ to itself, we identify
$L_F$ to itself, we identify ![]() $X$ as a subset of
$X$ as a subset of ![]() $L_F^n$. By the argument in § 3 of [Reference Gan and YuGY00] (in particular, Lemma 3.4), we know that
$L_F^n$. By the argument in § 3 of [Reference Gan and YuGY00] (in particular, Lemma 3.4), we know that
For any ![]() $\phi \in X$ regarded as a linear isometry from
$\phi \in X$ regarded as a linear isometry from ![]() $L_F$ to itself, the lattice
$L_F$ to itself, the lattice ![]() $L_\phi := \phi ^{-1}(M)$ is a lattice containing
$L_\phi := \phi ^{-1}(M)$ is a lattice containing ![]() $L$. Conversely, for any
$L$. Conversely, for any ![]() $L'$ containing
$L'$ containing ![]() $L$ and isometric to
$L$ and isometric to ![]() $M$, there is a
$M$, there is a ![]() $\phi \in X$ such that
$\phi \in X$ such that ![]() $L_\phi =L'$. Hence, we have a partition
$L_\phi =L'$. Hence, we have a partition
Since each ![]() $L'$ is isomorphic to
$L'$ is isomorphic to ![]() $M$, all the
$M$, all the ![]() $X_{L'}$ have the same volume as that of
$X_{L'}$ have the same volume as that of ![]() $X_M$. Specializing (6.5) to
$X_M$. Specializing (6.5) to ![]() $L=M$, we see
$L=M$, we see
Remark 6.3 When ![]() $F/F_0$ is unramified and
$F/F_0$ is unramified and ![]() $M$ is unimodular, the lemma was proved by (3.6.1.1) of [Reference Li and ZhangLZ22a].
$M$ is unimodular, the lemma was proved by (3.6.1.1) of [Reference Li and ZhangLZ22a].
Now we specialize Theorem 6.1 to the case ![]() $n=3$.
$n=3$.
Lemma 6.4 Assume ![]() $n=3$ and
$n=3$ and ![]() $\epsilon =\chi (L)$. Then
$\epsilon =\chi (L)$. Then ![]() $c_{3,1}^\epsilon ={q^2}/({1+q})$, hence
$c_{3,1}^\epsilon ={q^2}/({1+q})$, hence
Proof. First, according to Theorem 6.1,
By Corollary 5.8, we have
According to Lemmas A.8 and A.9,
Lemma 7.1 gives that
Hence,
and
Combining this with (6.7), we solve (6.2) and obtain
Now the lemma follows from (1.10).
7. Local density formula when  $\mathrm {rank}(T)\le 2$
$\mathrm {rank}(T)\le 2$
The main purpose of this section is to give an explicit formula for ![]() $\alpha (I, T, X)$ where
$\alpha (I, T, X)$ where ![]() $I=\mathrm {Diag}(I_{m-1}, \nu )$ with
$I=\mathrm {Diag}(I_{m-1}, \nu )$ with ![]() $\nu \in \mathcal {O}_{F_0}^\times$ and
$\nu \in \mathcal {O}_{F_0}^\times$ and ![]() $\mathrm {rank}(T)\le 2$.
$\mathrm {rank}(T)\le 2$.
7.1 The case  $T=(t)$
$T=(t)$
In order to apply induction formulas to calculate ![]() $\alpha (I, T, X)$ for
$\alpha (I, T, X)$ for ![]() $T$ with
$T$ with ![]() $\text {rank}(T) =2$, we need to consider the case
$\text {rank}(T) =2$, we need to consider the case ![]() $T=(t)$ first. Write
$T=(t)$ first. Write ![]() $t=t_0(-\pi _0)^{\mathrm {v}(t)}$ for
$t=t_0(-\pi _0)^{\mathrm {v}(t)}$ for ![]() $t_0\in \mathcal {O}_{F_0}^\times$, and
$t_0\in \mathcal {O}_{F_0}^\times$, and
for integers ![]() $0\le a \le b$.
$0\le a \le b$.
Lemma 7.1 Assume ![]() $0\le a\le b\le \mathrm {v}(t)$.
$0\le a\le b\le \mathrm {v}(t)$.
(1) If
 $m$ is odd, then
$m$ is odd, then
 \begin{align*} \alpha(I_{a,b},(t),X)&=1+\chi(I)\chi(-\nu_1)(q-1)\sum_{s=a+1}^{b}q^{-ms+a+({m-1})/{2}}X^s\\ &\quad +\chi(I_{a,b})\chi( t_0)q^{-(m+1)\mathrm{v}(t)+a+b-({m+1})/{2}}X^{\mathrm{v}(t)+1}. \end{align*}
\begin{align*} \alpha(I_{a,b},(t),X)&=1+\chi(I)\chi(-\nu_1)(q-1)\sum_{s=a+1}^{b}q^{-ms+a+({m-1})/{2}}X^s\\ &\quad +\chi(I_{a,b})\chi( t_0)q^{-(m+1)\mathrm{v}(t)+a+b-({m+1})/{2}}X^{\mathrm{v}(t)+1}. \end{align*}
(2) If
 $m$ is even, then
$m$ is even, then
 \begin{align*} \alpha(I_{a,b},(t),X)
&=1+\chi(I) (q-1) \sum_{s=1}^{a}q^{-(m-1)s+{m}/{2}-1}X^s\\
&\quad+\chi(I_{a,b}) q^{a+b}\biggl((q-1)
\sum_{s=b+1}^{\mathrm{v}(t)}q^{-(m+1)s+{m}/{2}} X^s -
q^{-(m+1)\mathrm{v}(t)-1-{m}/{2}}X^{\mathrm{v}(t)+1}\biggr).
\end{align*}
\begin{align*} \alpha(I_{a,b},(t),X)
&=1+\chi(I) (q-1) \sum_{s=1}^{a}q^{-(m-1)s+{m}/{2}-1}X^s\\
&\quad+\chi(I_{a,b}) q^{a+b}\biggl((q-1)
\sum_{s=b+1}^{\mathrm{v}(t)}q^{-(m+1)s+{m}/{2}} X^s -
q^{-(m+1)\mathrm{v}(t)-1-{m}/{2}}X^{\mathrm{v}(t)+1}\biggr).
\end{align*}
Proof. Direct calculation gives
 \begin{align*} \alpha(I_{a,b},(t),X)
&=\int_{F_0}\, dY \int_{\mathcal{O}_F^{2k+m+2}} \psi
(\langle Y, \mathrm{Diag}(\mathcal{H}^k,I_{a,b})[{\bf x}]-t
\rangle)\, d{\bf x} \nonumber\\ &=\int_{F_0} \psi(-tY)\, dY\\
&\quad \times \int_{\mathcal{O}_F^{2k} \times \mathcal{O}_F^{m+2}}\psi
\biggl( Y \sum_{i=1}^{k}
\mathrm{tr}\biggl(\frac{1}{\pi}x_i\bar{y}_i\biggr) +Y
\sum_{l=1}^{m+2}s_lz_l\bar{z}_{l}\biggr)
\prod_{i}\,dx_i \,dy_i \prod_{l}\,dz_l\nonumber\\
&=1+\sum_{s=1}^{\infty}\int_{\mathrm{v}(Y)=-s} I_k(Y)
I_{I_{a,b}}(Y)\psi(-tY) \, dY. \end{align*}
\begin{align*} \alpha(I_{a,b},(t),X)
&=\int_{F_0}\, dY \int_{\mathcal{O}_F^{2k+m+2}} \psi
(\langle Y, \mathrm{Diag}(\mathcal{H}^k,I_{a,b})[{\bf x}]-t
\rangle)\, d{\bf x} \nonumber\\ &=\int_{F_0} \psi(-tY)\, dY\\
&\quad \times \int_{\mathcal{O}_F^{2k} \times \mathcal{O}_F^{m+2}}\psi
\biggl( Y \sum_{i=1}^{k}
\mathrm{tr}\biggl(\frac{1}{\pi}x_i\bar{y}_i\biggr) +Y
\sum_{l=1}^{m+2}s_lz_l\bar{z}_{l}\biggr)
\prod_{i}\,dx_i \,dy_i \prod_{l}\,dz_l\nonumber\\
&=1+\sum_{s=1}^{\infty}\int_{\mathrm{v}(Y)=-s} I_k(Y)
I_{I_{a,b}}(Y)\psi(-tY) \, dY. \end{align*}
Here, according to [Reference ShiShi22, Lemma 7.6],
 \begin{align*} I_k(Y)=\int_{\mathcal{O}_F^{2k}}\psi
\biggl( Y \sum_{i=1}^{k} \mathrm{tr}\biggl(
\frac{1}{\pi}x_i\bar{y}_i\biggr)\biggr) \prod
\,dx_i \,dy_i= q^{-2ks} , \end{align*}
\begin{align*} I_k(Y)=\int_{\mathcal{O}_F^{2k}}\psi
\biggl( Y \sum_{i=1}^{k} \mathrm{tr}\biggl(
\frac{1}{\pi}x_i\bar{y}_i\biggr)\biggr) \prod
\,dx_i \,dy_i= q^{-2ks} , \end{align*}
and
 \begin{align*} I_{I_{a,b}}(Y)
=\int_{\mathcal{O}_F^{m+2}}\psi \biggl( Y
\sum_{l=1}^{m+2}s_lz_l\bar{z}_{l}\biggr) \prod
\,dz_l=\prod_{l=1}^{m+2} J(s_l Y), \end{align*}
\begin{align*} I_{I_{a,b}}(Y)
=\int_{\mathcal{O}_F^{m+2}}\psi \biggl( Y
\sum_{l=1}^{m+2}s_lz_l\bar{z}_{l}\biggr) \prod
\,dz_l=\prod_{l=1}^{m+2} J(s_l Y), \end{align*}
where
 \begin{equation} J(t) =\int_{\mathcal{O}_F} \psi(t z \bar z) \,dz = \begin{cases} 1, & \text{if } \mathrm{v}(t) \ge 0,\\ q^{\mathrm{v}(t)} \chi(-t_0) g\bigl(\chi,\psi_{{1}/{\pi_0}}\bigr), & \text{if } \mathrm{v}(t) <0, \end{cases} \end{equation}
\begin{equation} J(t) =\int_{\mathcal{O}_F} \psi(t z \bar z) \,dz = \begin{cases} 1, & \text{if } \mathrm{v}(t) \ge 0,\\ q^{\mathrm{v}(t)} \chi(-t_0) g\bigl(\chi,\psi_{{1}/{\pi_0}}\bigr), & \text{if } \mathrm{v}(t) <0, \end{cases} \end{equation}and
 \begin{align*} g(\chi,\psi_{{1}/{\pi_0}}) =\sum_{x \in \mathcal{O}_{F_0}/\pi_0} \chi(x) \psi\biggl(\frac{x}{\pi_0}\biggr) \end{align*}
\begin{align*} g(\chi,\psi_{{1}/{\pi_0}}) =\sum_{x \in \mathcal{O}_{F_0}/\pi_0} \chi(x) \psi\biggl(\frac{x}{\pi_0}\biggr) \end{align*}
is the Gauss sum. Write ![]() $\psi '=\psi _{{1}/{\pi _0}}$. Then
$\psi '=\psi _{{1}/{\pi _0}}$. Then
 \begin{align*}
&\alpha(I_{a,b},(t),X)\nonumber\\
&\quad=1+\sum_{s=1}^{a}q^{s}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-ms} \chi(\nu (-Y)^m)g(\chi,\psi')^{m}\psi(-(-\pi_0)^s
Yt) \,dY\nonumber\\ &\qquad
+\sum_{s=a+1}^{b}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-m s+a} \chi(\nu_1\nu
(-Y)^{m+1})g(\chi,\psi')^{m+1}\psi(-(-\pi_0)^{-s} Yt)\,
dY\nonumber\\
&\qquad+\sum_{s=b+1}^{\infty}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-(m+1)s+a+b} \chi(\nu_1\nu_2\nu
(-Y)^{m+2})g(\chi,\psi')^{m+2}\psi(-(-\pi_0)^{-s} Yt)\, dY.
\end{align*}
\begin{align*}
&\alpha(I_{a,b},(t),X)\nonumber\\
&\quad=1+\sum_{s=1}^{a}q^{s}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-ms} \chi(\nu (-Y)^m)g(\chi,\psi')^{m}\psi(-(-\pi_0)^s
Yt) \,dY\nonumber\\ &\qquad
+\sum_{s=a+1}^{b}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-m s+a} \chi(\nu_1\nu
(-Y)^{m+1})g(\chi,\psi')^{m+1}\psi(-(-\pi_0)^{-s} Yt)\,
dY\nonumber\\
&\qquad+\sum_{s=b+1}^{\infty}\int_{\mathcal{O}_{F_0}^{\times}}q^{-2ks}\cdot
q^{-(m+1)s+a+b} \chi(\nu_1\nu_2\nu
(-Y)^{m+2})g(\chi,\psi')^{m+2}\psi(-(-\pi_0)^{-s} Yt)\, dY.
\end{align*}
Recall the well-known facts that
 \begin{equation}
\begin{aligned} g(\chi,\psi')^2 & =\chi(-1)\cdot q, \\
\int_{\mathcal{O}_{F_0}^\times} \psi((-\pi_0)^{-s} Y t)
\,dY & = \operatorname{Char}(\pi_0^s\mathcal{O}_{F_0})(t) -
q^{-1}\operatorname{Char}(\pi_0^{s-1}\mathcal{O}_{F_0})(t),\\
\int_{\mathcal{O}_{F_0}^\times }\chi(Y)\psi((-\pi_0)^{-s} Y
t) \,dY & =\chi(-t_0) q^{-1} g(\chi,
\psi')\operatorname{Char}(\pi_0^{s-1}\mathcal{O}_{F_0}^\times)(t).
\end{aligned} \end{equation}
\begin{equation}
\begin{aligned} g(\chi,\psi')^2 & =\chi(-1)\cdot q, \\
\int_{\mathcal{O}_{F_0}^\times} \psi((-\pi_0)^{-s} Y t)
\,dY & = \operatorname{Char}(\pi_0^s\mathcal{O}_{F_0})(t) -
q^{-1}\operatorname{Char}(\pi_0^{s-1}\mathcal{O}_{F_0})(t),\\
\int_{\mathcal{O}_{F_0}^\times }\chi(Y)\psi((-\pi_0)^{-s} Y
t) \,dY & =\chi(-t_0) q^{-1} g(\chi,
\psi')\operatorname{Char}(\pi_0^{s-1}\mathcal{O}_{F_0}^\times)(t).
\end{aligned} \end{equation}
When ![]() $m$ is odd, we have
$m$ is odd, we have
 \begin{align*} \alpha(I_{a,b}, (t), X)&=1+\chi((-1)^{({m+1})/{2}}\nu_1\nu )(q-1)
\sum_{s=a+1}^{b}q^{-ms+a+({m-1})/{2}}X^s\\ &\quad +\chi((-1)^{({m+1})/{2}}\nu_1\nu_2\nu
t_0)q^{-(m+1)(\mathrm{v}(t)+1)+a+b+({m+1})/{2}}X^{\mathrm{v}(t)+1}.
\end{align*}
\begin{align*} \alpha(I_{a,b}, (t), X)&=1+\chi((-1)^{({m+1})/{2}}\nu_1\nu )(q-1)
\sum_{s=a+1}^{b}q^{-ms+a+({m-1})/{2}}X^s\\ &\quad +\chi((-1)^{({m+1})/{2}}\nu_1\nu_2\nu
t_0)q^{-(m+1)(\mathrm{v}(t)+1)+a+b+({m+1})/{2}}X^{\mathrm{v}(t)+1}.
\end{align*}
When ![]() $m$ is even, we have
$m$ is even, we have
 \begin{align*} &\alpha(I_{a,b}, (t),
X)\\ &\quad=1+\chi((-1)^{{m}/{2})}\nu) (q-1)
\sum_{s=1}^{a}q^{-(m-1)s+{m}/{2}-1}X^s +\chi((-1)
^{({m+2})/{2}}\nu_1\nu_2\nu)\\ &\qquad \cdot
\biggl((q-1)
\sum_{s=b+1}^{\mathrm{v}(t)}q^{-(m+1)s+a+b+{m}/{2}} X^s -
q^{-(m+1)(\mathrm{v}(t)+1)+a+b+{m}/{2}}X^{\mathrm{v}(t)+1}\biggr).
\end{align*}
\begin{align*} &\alpha(I_{a,b}, (t),
X)\\ &\quad=1+\chi((-1)^{{m}/{2})}\nu) (q-1)
\sum_{s=1}^{a}q^{-(m-1)s+{m}/{2}-1}X^s +\chi((-1)
^{({m+2})/{2}}\nu_1\nu_2\nu)\\ &\qquad \cdot
\biggl((q-1)
\sum_{s=b+1}^{\mathrm{v}(t)}q^{-(m+1)s+a+b+{m}/{2}} X^s -
q^{-(m+1)(\mathrm{v}(t)+1)+a+b+{m}/{2}}X^{\mathrm{v}(t)+1}\biggr).
\end{align*}
Finally, note that for ![]() $I$ of rank
$I$ of rank ![]() $m$ we have
$m$ we have
 \[ \chi(I)=\begin{cases} \chi((-1)^{({m-1})/{2}}\nu), & \text{if }m\text{ is odd},\\ \chi((-1)^{{m}/{2}}\nu), & \text{if }m\text{ is even}. \end{cases} \]
\[ \chi(I)=\begin{cases} \chi((-1)^{({m-1})/{2}}\nu), & \text{if }m\text{ is odd},\\ \chi((-1)^{{m}/{2}}\nu), & \text{if }m\text{ is even}. \end{cases} \]
Now the lemma is clear.
Similarly, we have the following lemma.
Lemma 7.2 Let ![]() $I$ be unimodular with odd rank
$I$ be unimodular with odd rank ![]() $m$. Then
$m$. Then
 \[ \alpha( I{\unicode{x29BA}} \mathcal{H}_{i},(t), X)=\begin{cases} 1+\chi(I)\chi( t_0)q^{-(\mathrm{v}(t)+1)(m+1)+({m+1})/{2}+i} X^{\mathrm{v}(t)+1}, & \text{if }i\le 2\mathrm{v}(t),\\ 1+\chi(I)\chi( t_0)q^{-(\mathrm{v}(t)+1)(m-1)+({m-1})/{2}}X^{\mathrm{v}(t)+1}, & \text{if }i> 2\mathrm{v}(t). \end{cases} \]
\[ \alpha( I{\unicode{x29BA}} \mathcal{H}_{i},(t), X)=\begin{cases} 1+\chi(I)\chi( t_0)q^{-(\mathrm{v}(t)+1)(m+1)+({m+1})/{2}+i} X^{\mathrm{v}(t)+1}, & \text{if }i\le 2\mathrm{v}(t),\\ 1+\chi(I)\chi( t_0)q^{-(\mathrm{v}(t)+1)(m-1)+({m-1})/{2}}X^{\mathrm{v}(t)+1}, & \text{if }i> 2\mathrm{v}(t). \end{cases} \]
7.2 The case  $T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$
$T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$
In this subsection, we compute ![]() $\alpha (I,T,X)$ for
$\alpha (I,T,X)$ for ![]() $I$ unimodular of rank
$I$ unimodular of rank ![]() $m\ge 2$ and
$m\ge 2$ and ![]() $T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with
$T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with ![]() $0\le a \le b$. Notice that
$0\le a \le b$. Notice that ![]() $\alpha (I, T, X)=0$ when
$\alpha (I, T, X)=0$ when ![]() $a<0$.
$a<0$.
Proposition 7.3 Assume ![]() $T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ and that
$T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ and that ![]() $I$ is isotropic of even rank
$I$ is isotropic of even rank ![]() $m \ge 2$, then
$m \ge 2$, then
 \begin{align*} \alpha(I,T,X)&=(1-X)\biggl(\sum_{i=0}^{a}(q^{2-m}X)^{i}+\gamma_e(I,T,X)\biggr)\\ &\quad+q X(q^{2-m}X)^{a}(1-\chi(I)q^{-({m}/{2})})( 1+ \chi(I)\chi(T)q^{({m-2})/{2}}(q^{2-m} X)^{b+1})\\ &\quad+ \big(1-q^{-(m-1)}+(q-1)\chi(I)q^{-({m}/{2})} \big) X\\ &\quad\cdot \biggl(q \sum_{i=0}^{a-1}(q^{2-m}X)^i+\gamma_e(I,T,X)-\chi(I)\chi(T)q^{{m}/{2}}(q^{2-m}X)^{a+b+1} \biggr), \end{align*}
\begin{align*} \alpha(I,T,X)&=(1-X)\biggl(\sum_{i=0}^{a}(q^{2-m}X)^{i}+\gamma_e(I,T,X)\biggr)\\ &\quad+q X(q^{2-m}X)^{a}(1-\chi(I)q^{-({m}/{2})})( 1+ \chi(I)\chi(T)q^{({m-2})/{2}}(q^{2-m} X)^{b+1})\\ &\quad+ \big(1-q^{-(m-1)}+(q-1)\chi(I)q^{-({m}/{2})} \big) X\\ &\quad\cdot \biggl(q \sum_{i=0}^{a-1}(q^{2-m}X)^i+\gamma_e(I,T,X)-\chi(I)\chi(T)q^{{m}/{2}}(q^{2-m}X)^{a+b+1} \biggr), \end{align*}
where
 \[ \gamma_{e}(I,T,X) = \chi(I)q^{{m}/{2}}\biggl(\sum_{d=1}^a(q^d-1)(q^{2-m}X)^{d} +\chi(T)q^a (q^{2-m}X)^{b+1}\sum_{i=0}^{a}(q^{1-m}X)^{i}\biggr). \]
\[ \gamma_{e}(I,T,X) = \chi(I)q^{{m}/{2}}\biggl(\sum_{d=1}^a(q^d-1)(q^{2-m}X)^{d} +\chi(T)q^a (q^{2-m}X)^{b+1}\sum_{i=0}^{a}(q^{1-m}X)^{i}\biggr). \]
Proof. Since ![]() $I$ is of even rank,
$I$ is of even rank, ![]() $u_1\cdot I^{[k]}\approx I^{[k]}$, and we may assume
$u_1\cdot I^{[k]}\approx I^{[k]}$, and we may assume ![]() $T$ is of the form
$T$ is of the form ![]() $\mathrm {Diag}( (-\pi _0)^a,u(-\pi _0)^b)$ without loss of generality.
$\mathrm {Diag}( (-\pi _0)^a,u(-\pi _0)^b)$ without loss of generality.
According to Theorem 5.2 and Proposition 5.9, we have
 \begin{align*} \alpha(I,T, X)&=\beta_1(I, (-\pi_0)^a,X) \alpha(M(1)^{\perp},u(-\pi_0)^b)\\ &\quad +q\beta_0(I, (-\pi_0)^a,X) \alpha(M(0)^{\perp},u(-\pi_0)^b) \\ &\quad +q^{2-m}X\alpha(I, \mathrm{Diag}((-\pi_0)^{a-1},u(-\pi_0)^b),X) \end{align*}
\begin{align*} \alpha(I,T, X)&=\beta_1(I, (-\pi_0)^a,X) \alpha(M(1)^{\perp},u(-\pi_0)^b)\\ &\quad +q\beta_0(I, (-\pi_0)^a,X) \alpha(M(0)^{\perp},u(-\pi_0)^b) \\ &\quad +q^{2-m}X\alpha(I, \mathrm{Diag}((-\pi_0)^{a-1},u(-\pi_0)^b),X) \end{align*}
where ![]() $M(1)^{\perp }=\mathrm {Diag}(\mathcal {H}^{k-1},-(-\pi _0)^i,I)$ and
$M(1)^{\perp }=\mathrm {Diag}(\mathcal {H}^{k-1},-(-\pi _0)^i,I)$ and
Continuing this process, we obtain
 \begin{align*}
\alpha(I,T,X)&=\sum_{i=0}^{a}(q^{2-m}X)^{a-i}\\
&\quad\cdot \big(\beta_1(I,(-\pi_0)^i,X)\alpha(M(1)^{\perp},u(-\pi_0)^b) +q\beta_0(I,(-\pi_0)^i,X)
\alpha(M(0)^{\perp},u(-\pi_0)^b)\big).
\end{align*}
\begin{align*}
\alpha(I,T,X)&=\sum_{i=0}^{a}(q^{2-m}X)^{a-i}\\
&\quad\cdot \big(\beta_1(I,(-\pi_0)^i,X)\alpha(M(1)^{\perp},u(-\pi_0)^b) +q\beta_0(I,(-\pi_0)^i,X)
\alpha(M(0)^{\perp},u(-\pi_0)^b)\big).
\end{align*}
By the formulas in Proposition 5.9 and Lemma 7.1, the above is equal to
 \begin{align*} &\sum_{i=0}^{a}(q^{2-m}X)^{a-i}(1-X)\\ &\quad\cdot \biggl(1+(q-1)\chi(I)q^{({m-2})/{2}}\sum_{s=-i}^{-1}(q^{(m-1)}(q^2 X)^{-1})^s+\chi(I)\chi(T)q^{i+{m}/{2}}(q^{2-m} X)^{b+1}\biggr)\\ &\quad+q (q^{2-m}X)^{a}X(1-q^{-({m}/{2})}\chi(I))( 1+ \chi(I)\chi(T)q^{-(b+1)(m-2)+({m-2})/{2}}X^{b+1})\\ &\quad+ q\sum_{i=1}^{a}(q^{2-m}X)^{a-i}X\big((1-q^{-(m-1)})+(q-1)\chi(I) q^{-(m-1)+({m-2})/{2}}\big)\\ &\quad\cdot \biggl(1+(q-1)\chi(I)q^{({m-4})/{2}}\sum_{s=-i}^{-1}(q^{(m-3)}X^{-1})^s+\chi(I)\chi(T) q^{i+({m-2})/{2}}(q^{2-m}X)^{b+1}\biggr). \end{align*}
\begin{align*} &\sum_{i=0}^{a}(q^{2-m}X)^{a-i}(1-X)\\ &\quad\cdot \biggl(1+(q-1)\chi(I)q^{({m-2})/{2}}\sum_{s=-i}^{-1}(q^{(m-1)}(q^2 X)^{-1})^s+\chi(I)\chi(T)q^{i+{m}/{2}}(q^{2-m} X)^{b+1}\biggr)\\ &\quad+q (q^{2-m}X)^{a}X(1-q^{-({m}/{2})}\chi(I))( 1+ \chi(I)\chi(T)q^{-(b+1)(m-2)+({m-2})/{2}}X^{b+1})\\ &\quad+ q\sum_{i=1}^{a}(q^{2-m}X)^{a-i}X\big((1-q^{-(m-1)})+(q-1)\chi(I) q^{-(m-1)+({m-2})/{2}}\big)\\ &\quad\cdot \biggl(1+(q-1)\chi(I)q^{({m-4})/{2}}\sum_{s=-i}^{-1}(q^{(m-3)}X^{-1})^s+\chi(I)\chi(T) q^{i+({m-2})/{2}}(q^{2-m}X)^{b+1}\biggr). \end{align*}
Now the transformation
 \[ \sum_{i=0}^a \sum_{s=1}^{i}q^s (q^{2-m}X)^{a-i+s} =\sum_{d=1}^a\sum_{s=1}^{d}q^s (q^{2-m}X)^d \]
\[ \sum_{i=0}^a \sum_{s=1}^{i}q^s (q^{2-m}X)^{a-i+s} =\sum_{d=1}^a\sum_{s=1}^{d}q^s (q^{2-m}X)^d \]
and some calculation gives us the result we want.
The case that ![]() $I$ is anisotropic (i.e. when
$I$ is anisotropic (i.e. when ![]() $m=2$ and
$m=2$ and ![]() $\chi (I)=-1$) can be computed similarly and is simpler. We omit the detail here. In particular, we may recover the following formula.
$\chi (I)=-1$) can be computed similarly and is simpler. We omit the detail here. In particular, we may recover the following formula.
Proposition 7.4 [Reference ShiShi22, Theorem 6.2(1)]
Assume ![]() $I=\mathrm {Diag}(1,\nu )$, then
$I=\mathrm {Diag}(1,\nu )$, then
 \begin{align*} &\alpha(I, T, X)\\ &\quad= (1-X) (1+ \chi(I) + q \chi(I)) \sum_{e=0}^\alpha (q X)^e -\chi(T) q^{\alpha+1} X^{\beta+1} (1-X) \sum_{e=0}^{\alpha} (q^{-1}X)^e\\ &\qquad -\chi(T) (1+q) ( X^{\alpha+ \beta +2}+\chi(I)\chi(T)) + (1+\chi(I)) q^{\alpha+1} X^{\alpha+1} (1+\chi(T) X^{\beta-\alpha}). \end{align*}
\begin{align*} &\alpha(I, T, X)\\ &\quad= (1-X) (1+ \chi(I) + q \chi(I)) \sum_{e=0}^\alpha (q X)^e -\chi(T) q^{\alpha+1} X^{\beta+1} (1-X) \sum_{e=0}^{\alpha} (q^{-1}X)^e\\ &\qquad -\chi(T) (1+q) ( X^{\alpha+ \beta +2}+\chi(I)\chi(T)) + (1+\chi(I)) q^{\alpha+1} X^{\alpha+1} (1+\chi(T) X^{\beta-\alpha}). \end{align*}
Moreover, a similar computation yields the following, and we leave the detail to reader.
Proposition 7.5 Assume that ![]() $I$ is unimodular of odd rank
$I$ is unimodular of odd rank ![]() $m\ge 3$. Then
$m\ge 3$. Then
 \begin{align*} &\alpha(I,T,X)\\
&\quad=(1\!-\!X)\biggl(\sum_{i=0}^{a}(q^{2-m} X)^{i} \!+\!\gamma_{o,1}(I,T,X)\biggr) \!+\!(1\!-\!q^{-(m-1)})X \biggl(q \sum_{i=0}^{a-1}(q^{2-m}
X)^{i}+\gamma_{o,0}(S,T,X)\biggr)\\
&\qquad +q X(q^{2-m} X)^{a} \big(1+\chi(I)\chi(u_1)q^{-({m-1})/{2}}\big)\big(1-\chi(I)\chi(u_1)
q^{(2-m)b-({m-1})/{2}}X^{b+1}\big),
\end{align*}
\begin{align*} &\alpha(I,T,X)\\
&\quad=(1\!-\!X)\biggl(\sum_{i=0}^{a}(q^{2-m} X)^{i} \!+\!\gamma_{o,1}(I,T,X)\biggr) \!+\!(1\!-\!q^{-(m-1)})X \biggl(q \sum_{i=0}^{a-1}(q^{2-m}
X)^{i}+\gamma_{o,0}(S,T,X)\biggr)\\
&\qquad +q X(q^{2-m} X)^{a} \big(1+\chi(I)\chi(u_1)q^{-({m-1})/{2}}\big)\big(1-\chi(I)\chi(u_1)
q^{(2-m)b-({m-1})/{2}}X^{b+1}\big),
\end{align*}
where ![]() $\gamma _{o,1}(I,T,X)$ equals
$\gamma _{o,1}(I,T,X)$ equals
 \[ \chi(I)\chi(u_1) q^{({m-1})/{2}}\biggl(\sum_{d=a+1}^{a+b}(q^{a+b+1-d}-1)(q^{2-m}X)^d-\sum_{i=b+1}^{a+b+1} (q^{2-m} X)^{i}\biggr), \]
\[ \chi(I)\chi(u_1) q^{({m-1})/{2}}\biggl(\sum_{d=a+1}^{a+b}(q^{a+b+1-d}-1)(q^{2-m}X)^d-\sum_{i=b+1}^{a+b+1} (q^{2-m} X)^{i}\biggr), \]
and ![]() $\gamma _{o,0}(I,T,X)$ equals
$\gamma _{o,0}(I,T,X)$ equals
 \[ \chi(I)\chi(u_1)q^{({m-1})/{2}}\biggl(\sum_{d=a+1}^{a+b}(q^{a+b+1-d}-q)(q^{2-m}X)^d-\sum_{i=b+1}^{a+b} (q^{2-m} X)^{i}\biggr). \]
\[ \chi(I)\chi(u_1)q^{({m-1})/{2}}\biggl(\sum_{d=a+1}^{a+b}(q^{a+b+1-d}-q)(q^{2-m}X)^d-\sum_{i=b+1}^{a+b} (q^{2-m} X)^{i}\biggr). \]
8. Local density formula when  $\mathrm {rank}(T)=3$
$\mathrm {rank}(T)=3$
In this section, we always assume ![]() $\mathrm {rank}(T)=3$ and
$\mathrm {rank}(T)=3$ and ![]() $S=I_3^{-\chi (T)}$. The aim of this section is to compute
$S=I_3^{-\chi (T)}$. The aim of this section is to compute ![]() $\partial \mathrm {Den}(T)$ explicitly. We treat the case
$\partial \mathrm {Den}(T)$ explicitly. We treat the case ![]() $\mathrm {v}(T)\le -1$ in the first subsection. In the second subsection, we deal with the case when
$\mathrm {v}(T)\le -1$ in the first subsection. In the second subsection, we deal with the case when ![]() $T=\mathrm {Diag}(1,T_2)$ for
$T=\mathrm {Diag}(1,T_2)$ for ![]() $T_2$ diagonal. In the last subsection, instead of
$T_2$ diagonal. In the last subsection, instead of ![]() $\partial \mathrm {Den}(T)$, we compute
$\partial \mathrm {Den}(T)$, we compute ![]() $\partial \mathrm {Den}(T)^{(2)}$ for
$\partial \mathrm {Den}(T)^{(2)}$ for ![]() $T$ of the form not covered by previous subsections.
$T$ of the form not covered by previous subsections.
8.1  $\partial \mathrm {Den}(T)$ for
$\partial \mathrm {Den}(T)$ for  $T$ with
$T$ with  $\mathrm {v}(T)\le -1$
$\mathrm {v}(T)\le -1$
Proposition 8.1 If ![]() $\mathrm {v}(T)\le -1$, then
$\mathrm {v}(T)\le -1$, then ![]() $\mathrm {Int}(T)=\partial \mathrm {Den} (T)=0$.
$\mathrm {Int}(T)=\partial \mathrm {Den} (T)=0$.
Proof. If ![]() $\mathrm {v}(T)< -1$, then
$\mathrm {v}(T)< -1$, then ![]() $\partial \mathrm {Den} (T)=0$ since
$\partial \mathrm {Den} (T)=0$ since ![]() $\mathrm {v}(S^{[k]})\ge -1$. If
$\mathrm {v}(S^{[k]})\ge -1$. If ![]() $\mathrm {v}(T)= -1$, then
$\mathrm {v}(T)= -1$, then ![]() $T$ is of the form
$T$ is of the form ![]() $\mathrm {Diag}(\mathcal {H},(u_3(-\pi _0)^c))$ with
$\mathrm {Diag}(\mathcal {H},(u_3(-\pi _0)^c))$ with ![]() $\chi (T)=\chi (u_3)$. In this case, according to Corollary 5.8, Lemmas A.8 and A.9, we have
$\chi (T)=\chi (u_3)$. In this case, according to Corollary 5.8, Lemmas A.8 and A.9, we have
Similarly, we have
 \begin{align*} \alpha(\mathcal{H}^{3,1}_{\chi(T)},T)&=\beta(\mathcal{H}^{3,1}_{\chi(T)},\mathcal{H})\alpha(u_3,(u_3(-\pi_0)^c))\\ &=(1-q^{-2})\alpha(u_3,(u_3(-\pi_0)^c)). \end{align*}
\begin{align*} \alpha(\mathcal{H}^{3,1}_{\chi(T)},T)&=\beta(\mathcal{H}^{3,1}_{\chi(T)},\mathcal{H})\alpha(u_3,(u_3(-\pi_0)^c))\\ &=(1-q^{-2})\alpha(u_3,(u_3(-\pi_0)^c)). \end{align*}
Hence, applying Lemma 7.1 to ![]() $I_{0,0}=S$ where
$I_{0,0}=S$ where ![]() $I$ is of rank 1, we have
$I$ is of rank 1, we have
 \begin{align*} \partial \mathrm{Den}(T)&=2\alpha(S,(u_3(-\pi_0)^c),q^2)+\frac{q^2}{1+q}(1-q^{-2})\alpha((u_3),(u_3(-\pi_0)^c))\\ &=2(1+\chi(S)\chi(u_3)q)+2(q-1)\\ &=2(1-q)+2(q-1)\\ &=0. \end{align*}
\begin{align*} \partial \mathrm{Den}(T)&=2\alpha(S,(u_3(-\pi_0)^c),q^2)+\frac{q^2}{1+q}(1-q^{-2})\alpha((u_3),(u_3(-\pi_0)^c))\\ &=2(1+\chi(S)\chi(u_3)q)+2(q-1)\\ &=2(1-q)+2(q-1)\\ &=0. \end{align*}
Here we are using the fact ![]() $\chi (S)\chi (T)=\chi (S)\chi (u_3)=-1$.
$\chi (S)\chi (T)=\chi (S)\chi (u_3)=-1$.
8.2  $\partial \mathrm {Den}(T)$ for
$\partial \mathrm {Den}(T)$ for  $T=\mathrm {Diag}(1,T_2)$ with
$T=\mathrm {Diag}(1,T_2)$ with  $T_2$ diagonal
$T_2$ diagonal
In this subsection, we assume ![]() $T=\mathrm {Diag}(1,T_2)$, where
$T=\mathrm {Diag}(1,T_2)$, where ![]() $T_2=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with
$T_2=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with ![]() $0\le a\le b$. Let
$0\le a\le b$. Let ![]() $u=u_1u_2$. In addition, let
$u=u_1u_2$. In addition, let ![]() $S=\mathrm {Diag}(1,1,\nu )$ and
$S=\mathrm {Diag}(1,1,\nu )$ and ![]() $S_2=\mathrm {Diag}(1,\nu )$. We compare
$S_2=\mathrm {Diag}(1,\nu )$. We compare ![]() $\partial \mathrm {Den}(T)$ and
$\partial \mathrm {Den}(T)$ and ![]() $\partial \mathrm {Den}(T_2)$ in this subsection.
$\partial \mathrm {Den}(T_2)$ in this subsection.
Recall that
 \[ \partial \mathrm{Den}(T)=2\frac{\alpha'(S,T)}{\alpha(S,S)}+\frac{q^2}{1+q}\frac{\alpha(\mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}. \]
\[ \partial \mathrm{Den}(T)=2\frac{\alpha'(S,T)}{\alpha(S,S)}+\frac{q^2}{1+q}\frac{\alpha(\mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}. \]
Moreover, according to [Reference ShiShi22, Theorem 1.3] and [Reference He, Shi and YangHSY23, Theorem 1.1], the analytic side in the case ![]() $n=2$ is
$n=2$ is
Proposition 8.2
 \[ \partial \mathrm{Den}(T)-\partial \mathrm{Den}(T_2)=\begin{cases} 1+2\displaystyle\sum_{i=1}^a q^i, & \text{if }\chi(T)=1,\\ 1, & \text{if }\chi(T)=-1. \end{cases} \]
\[ \partial \mathrm{Den}(T)-\partial \mathrm{Den}(T_2)=\begin{cases} 1+2\displaystyle\sum_{i=1}^a q^i, & \text{if }\chi(T)=1,\\ 1, & \text{if }\chi(T)=-1. \end{cases} \]
Proof. Proposition 5.9 implies that ![]() $\alpha (S,T,X)$ equals
$\alpha (S,T,X)$ equals
Hence,
According to Lemma A.11, one can check that ![]() $\alpha (S,S)=\beta (S,S)=2q(q^2-1)$, and
$\alpha (S,S)=\beta (S,S)=2q(q^2-1)$, and ![]() $\alpha (S_2,S_2)=2(q-\chi (S_2))$. Then
$\alpha (S_2,S_2)=2(q-\chi (S_2))$. Then
Hence, we just need to check that
 \begin{align*} &2\frac{\alpha( \mathrm{Diag}(-1,S),T_2,q^2 )}{\alpha(S,S)}+ \frac{q^2}{1+q^2}\frac{\alpha( \mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}+\frac{2q^2}{q^2-1}\frac{\alpha(\mathcal{H},T_2)}{\alpha(S_2,S_2)}\\ &\quad=\begin{cases} 1+2\displaystyle\sum_{i=1}^a q^i, & \text{if }\chi(T)=1,\\ 1, & \text{if }\chi(T)=-1. \end{cases} \end{align*}
\begin{align*} &2\frac{\alpha( \mathrm{Diag}(-1,S),T_2,q^2 )}{\alpha(S,S)}+ \frac{q^2}{1+q^2}\frac{\alpha( \mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}+\frac{2q^2}{q^2-1}\frac{\alpha(\mathcal{H},T_2)}{\alpha(S_2,S_2)}\\ &\quad=\begin{cases} 1+2\displaystyle\sum_{i=1}^a q^i, & \text{if }\chi(T)=1,\\ 1, & \text{if }\chi(T)=-1. \end{cases} \end{align*}
By Proposition 7.3, we may check that
 \begin{equation} 2\alpha(\mathrm{Diag}(-1,S),T_2,q^2)= \begin{cases} 2(2q^{a+2}-(q+1)^2)(q-1), & \text{if }\chi(T)=1,\\ 2(q-1)(q^2-1), & \text{if }\chi(T)=-1. \end{cases} \end{equation}
\begin{equation} 2\alpha(\mathrm{Diag}(-1,S),T_2,q^2)= \begin{cases} 2(2q^{a+2}-(q+1)^2)(q-1), & \text{if }\chi(T)=1,\\ 2(q-1)(q^2-1), & \text{if }\chi(T)=-1. \end{cases} \end{equation}
To compute ![]() $({q^2}/({1+q}))\alpha (\mathcal {H}^{3,1}_{\chi (T)},T)$, we may choose
$({q^2}/({1+q}))\alpha (\mathcal {H}^{3,1}_{\chi (T)},T)$, we may choose ![]() $\mathcal {H}^{3,1}_{\chi (T)}=\mathrm {Diag}(\mathcal {H}, 1)$ when
$\mathcal {H}^{3,1}_{\chi (T)}=\mathrm {Diag}(\mathcal {H}, 1)$ when ![]() $\chi (T)=1$. By Corollary 5.8, Proposition 7.4, and a direct calculation, we have
$\chi (T)=1$. By Corollary 5.8, Proposition 7.4, and a direct calculation, we have
 \[ \frac{q^2}{1+q}\frac{\alpha(\mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)} =\frac{1}{2q(q^2-1)}\cdot\begin{cases} (q-1) \alpha(\mathrm{Diag}(-1,1),T_2)+\dfrac{2q^2}{q-1} \alpha(\mathcal{H},T_2), & \text{if }\chi(T)=1,\\ (q-1) \alpha(\mathrm{Diag}(-1,-u),T_2), & \text{if }\chi(T)=-1. \end{cases} \]
\[ \frac{q^2}{1+q}\frac{\alpha(\mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)} =\frac{1}{2q(q^2-1)}\cdot\begin{cases} (q-1) \alpha(\mathrm{Diag}(-1,1),T_2)+\dfrac{2q^2}{q-1} \alpha(\mathcal{H},T_2), & \text{if }\chi(T)=1,\\ (q-1) \alpha(\mathrm{Diag}(-1,-u),T_2), & \text{if }\chi(T)=-1. \end{cases} \]
Combining this with the formulas in [Reference He, Shi and YangHSY23, Theorem 6.1], we have
 \begin{equation} \frac{q^2}{1+q^2}\frac{\alpha( \mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}+\frac{2q^2}{q^2-1}\frac{\alpha(\mathcal{H},T_2)}{\alpha(S_2,S_2)} =\frac{1}{q(q^2-1)}\cdot\begin{cases} 4q^{a+2}-q^2-2q-1, & \text{if }\chi(T)=1,\\ (q^2-1), & \text{if }\chi(T)=-1. \end{cases} \end{equation}
\begin{equation} \frac{q^2}{1+q^2}\frac{\alpha( \mathcal{H}^{3,1}_{\chi(T)},T)}{\alpha(S,S)}+\frac{2q^2}{q^2-1}\frac{\alpha(\mathcal{H},T_2)}{\alpha(S_2,S_2)} =\frac{1}{q(q^2-1)}\cdot\begin{cases} 4q^{a+2}-q^2-2q-1, & \text{if }\chi(T)=1,\\ (q^2-1), & \text{if }\chi(T)=-1. \end{cases} \end{equation}Now a direct computation combined with (8.3) and (8.4) proves the proposition.
Corollary 8.3 Assume ![]() $L$ is a Hermitian lattice with Gram matrix
$L$ is a Hermitian lattice with Gram matrix ![]() $T$, then
$T$, then
Proof. We can write ![]() $L=L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x}$ where
$L=L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x}$ where ![]() $q({\bf x})=1$. If
$q({\bf x})=1$. If ![]() $L^\flat$ is non-split, then
$L^\flat$ is non-split, then ![]() $|\{\mathcal {V}^0(L)\}|=1$.
$|\{\mathcal {V}^0(L)\}|=1$.
If ![]() $L^\flat$ is split, then
$L^\flat$ is split, then ![]() $|\{\mathcal {V}^0(L)\}|= 1+2\sum _{i=1}^a q^i$ since
$|\{\mathcal {V}^0(L)\}|= 1+2\sum _{i=1}^a q^i$ since ![]() $\mathcal {L}_3(L)$ can be identified with
$\mathcal {L}_3(L)$ can be identified with ![]() $\mathcal {L}_{2,1}(L^\flat )$, which is a ball in
$\mathcal {L}_{2,1}(L^\flat )$, which is a ball in ![]() $\mathcal {L}_{2,1}$ centered at a vertex lattice of type
$\mathcal {L}_{2,1}$ centered at a vertex lattice of type ![]() $0$ with radius
$0$ with radius ![]() $a$ (see [Reference He, Shi and YangHSY23] for more detail). Here
$a$ (see [Reference He, Shi and YangHSY23] for more detail). Here ![]() $\mathcal {L}_{2,1}$ is the Bruhat–Tits tree associated with
$\mathcal {L}_{2,1}$ is the Bruhat–Tits tree associated with ![]() $\mathcal {N}^{\mathrm {Kra}}_{2,1}$ and
$\mathcal {N}^{\mathrm {Kra}}_{2,1}$ and ![]() $\mathcal {L}_{2,1}(L^\flat )$ is the subtree of
$\mathcal {L}_{2,1}(L^\flat )$ is the subtree of ![]() $\mathcal {L}_{2,1}$ associated with
$\mathcal {L}_{2,1}$ associated with ![]() $L^\flat$.
$L^\flat$.
8.3  $\partial \mathrm {Den}(T)^{(2)}$
$\partial \mathrm {Den}(T)^{(2)}$
In this subsection, we assume ![]() $T=\mathrm {Diag}(T_2,u_3(-\pi _0)^c)$ with
$T=\mathrm {Diag}(T_2,u_3(-\pi _0)^c)$ with ![]() $\mathrm {v}(T_2)>0$, and compute
$\mathrm {v}(T_2)>0$, and compute ![]() $\partial \mathrm {Den}(T)^{(2)}$. Recall that
$\partial \mathrm {Den}(T)^{(2)}$. Recall that ![]() $\partial \mathrm {Den}(T)^{(2)}=\partial \mathrm {Den}(L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x})^{(2)}$ where the Gram matrix of
$\partial \mathrm {Den}(T)^{(2)}=\partial \mathrm {Den}(L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x})^{(2)}$ where the Gram matrix of ![]() $L=L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x}$ is
$L=L^\flat {\unicode{x29BA}} \mathcal {O}_F {\bf x}$ is ![]() $T$. We consider two cases separately in Propositions 8.4 and 8.5.
$T$. We consider two cases separately in Propositions 8.4 and 8.5.
Proposition 8.4 Let ![]() $T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b, u_3(-\pi _0)^c)$ where
$T=\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b, u_3(-\pi _0)^c)$ where ![]() $0< a\le b \le c$. Then
$0< a\le b \le c$. Then
Proof. Recall that
We compute ![]() $\beta '(S,T)^{(2)}$ first. According to Proposition 5.10,
$\beta '(S,T)^{(2)}$ first. According to Proposition 5.10, ![]() $\beta _0(S,T_2,X)=0$ and
$\beta _0(S,T_2,X)=0$ and
 \begin{align*} \beta(S,T,X)^{(2)}& =\beta_2(S,T_2,X)\alpha(\mathrm{Diag}(S,-T_2),u_3(-\pi_0)^c,q^4 X)\\ &\quad +q \beta_1(S,T_2,X)\alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X)\\ &=(1-X)(1-q^2 X)\alpha(\mathrm{Diag}(S,-T_2),u_3(-\pi_0)^c,q^4 X) \\ &\quad+(q+1)(q^2-1)X(1-X) \alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X). \end{align*}
\begin{align*} \beta(S,T,X)^{(2)}& =\beta_2(S,T_2,X)\alpha(\mathrm{Diag}(S,-T_2),u_3(-\pi_0)^c,q^4 X)\\ &\quad +q \beta_1(S,T_2,X)\alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X)\\ &=(1-X)(1-q^2 X)\alpha(\mathrm{Diag}(S,-T_2),u_3(-\pi_0)^c,q^4 X) \\ &\quad+(q+1)(q^2-1)X(1-X) \alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X). \end{align*}
According to Lemma 7.1,
 \begin{align*}
\alpha(\mathrm{Diag}(S, -T_2),u_3(-\pi_0)^c,q^4 X) &=1+\chi(S)\chi(u_1)(q-1)\\
&\quad\times\sum_{s=a+1}^bq^{a+1}(q X)^s +\chi(u_1u_2u_3\nu)q^{a+b+2} X^{c+1},
\end{align*}
\begin{align*}
\alpha(\mathrm{Diag}(S, -T_2),u_3(-\pi_0)^c,q^4 X) &=1+\chi(S)\chi(u_1)(q-1)\\
&\quad\times\sum_{s=a+1}^bq^{a+1}(q X)^s +\chi(u_1u_2u_3\nu)q^{a+b+2} X^{c+1},
\end{align*}
and
 \begin{align*}
\alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X) &=1+\chi(S)\chi(u_1)(q-1)q^a\\
&\quad\times\sum_{s=a+1}^b(q X)^s+\chi(u_1u_2u_3\nu)q^{a+b+1}X^{c+1}.
\end{align*}
\begin{align*}
\alpha(\mathrm{Diag}(-\nu,-T_2),u_3(-\pi_0)^c,q^2 X) &=1+\chi(S)\chi(u_1)(q-1)q^a\\
&\quad\times\sum_{s=a+1}^b(q X)^s+\chi(u_1u_2u_3\nu)q^{a+b+1}X^{c+1}.
\end{align*}
The relation ![]() $\chi (u_1u_2u_3\nu )=\chi (S)\chi (T)=-1$ and a direct calculation show that
$\chi (u_1u_2u_3\nu )=\chi (S)\chi (T)=-1$ and a direct calculation show that
Finally, ![]() $\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}=0$ by Proposition 5.10. The proposition is proved.
$\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}=0$ by Proposition 5.10. The proposition is proved.
Proposition 8.5 Recall that ![]() $\mathcal {H}_a=\bigl (\begin {smallmatrix} 0 & \pi ^a\\ (-\pi )^a & 0\end {smallmatrix}\bigr )$. Let
$\mathcal {H}_a=\bigl (\begin {smallmatrix} 0 & \pi ^a\\ (-\pi )^a & 0\end {smallmatrix}\bigr )$. Let ![]() $T= \mathrm {Diag}(\mathcal {H}_a, u_3(-\pi _0)^c)$ where
$T= \mathrm {Diag}(\mathcal {H}_a, u_3(-\pi _0)^c)$ where ![]() $a$ is a positive odd integer and
$a$ is a positive odd integer and ![]() $c\ge 0$. Then
$c\ge 0$. Then
 \[ \partial \mathrm{Den}(T)^{(2)}= \begin{cases} (1-q^{a}), & \text{if }a\le 2c,\\ (1-q^{2c+1}), & \text{if }a> 2c. \end{cases} \]
\[ \partial \mathrm{Den}(T)^{(2)}= \begin{cases} (1-q^{a}), & \text{if }a\le 2c,\\ (1-q^{2c+1}), & \text{if }a> 2c. \end{cases} \]
Proof. Recall that
We need to compute ![]() $\beta '(S,T)^{(2)}$ and
$\beta '(S,T)^{(2)}$ and ![]() $\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}$.
$\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}$.
According to Proposition 5.10, ![]() $\beta _0(S,T_2,X)=0$ and
$\beta _0(S,T_2,X)=0$ and
 \begin{align*} \beta(S,T,X)^{(2)} &=\beta_2(S,\mathcal{H}_a,X)\alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)\\ &\quad +q \beta_1(S,\mathcal{H}_a,X) \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)\\ &=(1-X)\bigl((1-q^2 X)\alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)\\ &\quad +(q+1)(q^2-1)X \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)\bigr). \end{align*}
\begin{align*} \beta(S,T,X)^{(2)} &=\beta_2(S,\mathcal{H}_a,X)\alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)\\ &\quad +q \beta_1(S,\mathcal{H}_a,X) \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)\\ &=(1-X)\bigl((1-q^2 X)\alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)\\ &\quad +(q+1)(q^2-1)X \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)\bigr). \end{align*}
According to Lemma 7.2,
 \[ \alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)= \begin{cases} 1+\chi(S)\chi(u_3)q^{2+a} X^{c+1}, & \text{if }a\le 2c,\\ 1+ \chi(S)\chi(u_3)q^{2c+3} X^{c+1}, & \text{if }a> 2c, \end{cases} \]
\[ \alpha(\mathrm{Diag}(S, \mathcal{H}_a),u_3(-\pi_0)^c,q^4 X)= \begin{cases} 1+\chi(S)\chi(u_3)q^{2+a} X^{c+1}, & \text{if }a\le 2c,\\ 1+ \chi(S)\chi(u_3)q^{2c+3} X^{c+1}, & \text{if }a> 2c, \end{cases} \]
and
 \[ \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)=\begin{cases} 1+\chi(S)\chi(u_3)q^{1+a} X^{c+1}, & \text{if }a\le 2c,\\ 1+ \chi(S)\chi(u_3)q^{2c+2} X^{c+1}, & \text{if }a> 2c. \end{cases} \]
\[ \alpha(\mathrm{Diag}( -\nu,\mathcal{H}_a),u_3(-\pi_0)^c,q^2 X)=\begin{cases} 1+\chi(S)\chi(u_3)q^{1+a} X^{c+1}, & \text{if }a\le 2c,\\ 1+ \chi(S)\chi(u_3)q^{2c+2} X^{c+1}, & \text{if }a> 2c. \end{cases} \]
A short computation shows that
 \[ \beta'(S,T)^{(2)}=q(q^2-1) \cdot \begin{cases} 1+\chi(S)\chi(u_3)q^{a}, & \text{if }a\le 2c,\\ 1+\chi(S)\chi(u_3)q^{2c+1}, & \text{if }a> 2c. \end{cases} \]
\[ \beta'(S,T)^{(2)}=q(q^2-1) \cdot \begin{cases} 1+\chi(S)\chi(u_3)q^{a}, & \text{if }a\le 2c,\\ 1+\chi(S)\chi(u_3)q^{2c+1}, & \text{if }a> 2c. \end{cases} \]
Note that ![]() $\chi (S)\chi (u_3)=\chi (S)\chi (T)=-1$. Finally,
$\chi (S)\chi (u_3)=\chi (S)\chi (T)=-1$. Finally, ![]() $\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}=0$ by Proposition 5.10. The proposition is proved.
$\beta (\mathcal {H}^{3,1}_{\chi (T)},T)^{(2)}=0$ by Proposition 5.10. The proposition is proved.
Part 3. Proof of the main theorem
9. Reduced locus of special cycle
As remarked in § 2, results of [Reference Rapoport, Terstiege and WilsonRTW14] extend to the category of strict formal ![]() $\mathcal {O}_{F_0}$-modules using relative Dieudonné theory.
$\mathcal {O}_{F_0}$-modules using relative Dieudonné theory.
9.1 The Bruhat–Tits building for  $n=3$
$n=3$
From now on we assume ![]() $n=3$ and
$n=3$ and ![]() $\mathcal {L}=\mathcal {L}_3$ as in § 2.3.
$\mathcal {L}=\mathcal {L}_3$ as in § 2.3.
Lemma 9.1
(1) For every
 $\Lambda _2\in \mathcal {V}^2$,
$\Lambda _2\in \mathcal {V}^2$,  $\mathcal {N}_{\Lambda _2}$ is isomorphic to the projective line
$\mathcal {N}_{\Lambda _2}$ is isomorphic to the projective line  $\mathbb {P}^1$ over
$\mathbb {P}^1$ over  $k$. Its
$k$. Its  $q+1$ rational points correspond to all
$q+1$ rational points correspond to all  $\Lambda _0\in \mathcal {V}^0$ contained in
$\Lambda _0\in \mathcal {V}^0$ contained in  $\Lambda _2$.
$\Lambda _2$.(2) Every
 $\Lambda _0\in \mathcal {V}^0$ is contained in
$\Lambda _0\in \mathcal {V}^0$ is contained in  $q+1$ type
$q+1$ type  $2$ lattices. In other words, there are
$2$ lattices. In other words, there are  $q+1$ projective lines in
$q+1$ projective lines in  $(\mathcal {N}_3^\mathrm {Pap})_{\mathrm {red}}$ passing through the superspecial point
$(\mathcal {N}_3^\mathrm {Pap})_{\mathrm {red}}$ passing through the superspecial point  $\mathcal {N}_{\Lambda _0}(k)$. Moreover,
(9.1)
$\mathcal {N}_{\Lambda _0}(k)$. Moreover,
(9.1) \begin{equation} \bigcap_{\Lambda_2\in \mathcal{V}_2, \Lambda_0 \subset \Lambda_2} \Lambda_2^\sharp=\pi \Lambda_0. \end{equation}
\begin{equation} \bigcap_{\Lambda_2\in \mathcal{V}_2, \Lambda_0 \subset \Lambda_2} \Lambda_2^\sharp=\pi \Lambda_0. \end{equation}
Proof. Suppose ![]() $z\in \mathcal {N}(k)$ and
$z\in \mathcal {N}(k)$ and ![]() $M:= M(z)\subset N$ is defined as in Proposition 2.9. Since
$M:= M(z)\subset N$ is defined as in Proposition 2.9. Since ![]() $n=3$, by [Reference Rapoport, Terstiege and WilsonRTW14, Proposition 4.1] we have
$n=3$, by [Reference Rapoport, Terstiege and WilsonRTW14, Proposition 4.1] we have ![]() $\Lambda (M)\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}=M+\tau (M)$.
$\Lambda (M)\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}=M+\tau (M)$.
Proof of part (1). Suppose ![]() $z\in \mathcal {N}_{\Lambda _2}(k)$, i.e.
$z\in \mathcal {N}_{\Lambda _2}(k)$, i.e. ![]() $M\subset \Lambda _2$.
$M\subset \Lambda _2$.
If ![]() $M=\tau (M)$, then
$M=\tau (M)$, then ![]() $M=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ for some
$M=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ for some ![]() $\Lambda _0\in \mathcal {V}^0$ contained in
$\Lambda _0\in \mathcal {V}^0$ contained in ![]() $\Lambda _2$.
$\Lambda _2$.
If ![]() $M\neq \tau (M)$, then by taking the dual of
$M\neq \tau (M)$, then by taking the dual of ![]() $M\subset \Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ we have the following sequence of inclusions
$M\subset \Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$ we have the following sequence of inclusions
In both cases the class of ![]() $M$ in
$M$ in ![]() $\Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}/(\Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F})^\sharp \cong k^2$ is a line. This finishes the proof of part (1).
$\Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}/(\Lambda _2\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F})^\sharp \cong k^2$ is a line. This finishes the proof of part (1).
Proof of part (2). For each ![]() $\Lambda _0\in \mathcal {V}^0$ we just need to count the number of lattices
$\Lambda _0\in \mathcal {V}^0$ we just need to count the number of lattices ![]() $\Lambda _2\in \mathcal {V}^2$ that contains
$\Lambda _2\in \mathcal {V}^2$ that contains ![]() $\Lambda _0$. We have the following sequence of inclusions
$\Lambda _0$. We have the following sequence of inclusions
With respect to the quadratic form ![]() $(\,{,}\,)\pmod {\pi }$ on
$(\,{,}\,)\pmod {\pi }$ on ![]() $\Lambda _0/\pi \Lambda _0$, the dual lattice
$\Lambda _0/\pi \Lambda _0$, the dual lattice ![]() $\Lambda _2^\sharp$ corresponds to the
$\Lambda _2^\sharp$ corresponds to the ![]() $2$-dimensional subspaces
$2$-dimensional subspaces ![]() $U:= \Lambda _2^\sharp /\pi \Lambda _0$ in
$U:= \Lambda _2^\sharp /\pi \Lambda _0$ in ![]() $\Lambda _0/\pi \Lambda _0$ such that
$\Lambda _0/\pi \Lambda _0$ such that ![]() $U^\bot \stackrel {1}{\subset } U$. Thus, we just need to count the number of isotropic lines
$U^\bot \stackrel {1}{\subset } U$. Thus, we just need to count the number of isotropic lines ![]() $U^\bot$. Assume that
$U^\bot$. Assume that ![]() $\{e_1,e_2,e_3\}$ is a basis of
$\{e_1,e_2,e_3\}$ is a basis of ![]() $\Lambda _0/\pi \Lambda _0$ whose Gram matrix with respect to the quadratic form
$\Lambda _0/\pi \Lambda _0$ whose Gram matrix with respect to the quadratic form ![]() $(\,{,}\,)_\mathbb {X} \pmod \pi$ is
$(\,{,}\,)_\mathbb {X} \pmod \pi$ is
 \[ \left(\begin{array}{ccc} & 1 & \\ 1 & & \\ & & \epsilon \end{array}\right). \]
\[ \left(\begin{array}{ccc} & 1 & \\ 1 & & \\ & & \epsilon \end{array}\right). \]
It is easy to see that the isotropic lines are ![]() $\mathrm {Span}\{e_1\}$,
$\mathrm {Span}\{e_1\}$, ![]() $\mathrm {Span}\{e_2\}$ and
$\mathrm {Span}\{e_2\}$ and ![]() $\mathrm {Span}\{e_1-({\epsilon a^2}/{2})e_2+a e_3\}$ (
$\mathrm {Span}\{e_1-({\epsilon a^2}/{2})e_2+a e_3\}$ (![]() $a\in \mathbb {F}_q^\times$). Finally, (9.1) can be checked directly using this basis.
$a\in \mathbb {F}_q^\times$). Finally, (9.1) can be checked directly using this basis.
It is well known that ![]() $\mathcal {L}$ is a tree; see, for example, [Reference BrownBro89, § 3 of Chapter VI]. More specifically, the vertices of
$\mathcal {L}$ is a tree; see, for example, [Reference BrownBro89, § 3 of Chapter VI]. More specifically, the vertices of ![]() $\mathcal {L}$ correspond to vertex lattices of type
$\mathcal {L}$ correspond to vertex lattices of type ![]() $2$ or
$2$ or ![]() $0$. There is an edge between
$0$. There is an edge between ![]() $\Lambda \in \mathcal {V}^2$ and
$\Lambda \in \mathcal {V}^2$ and ![]() $\Lambda _0\in \mathcal {V}^0$ if
$\Lambda _0\in \mathcal {V}^0$ if ![]() $\Lambda _0\subset \Lambda$. We give each edge length
$\Lambda _0\subset \Lambda$. We give each edge length ![]() $\tfrac {1}{2}$. This defines a metric
$\tfrac {1}{2}$. This defines a metric ![]() $d(\,{,}\,)$ on
$d(\,{,}\,)$ on ![]() $\mathcal {L}$. Recall that we have defined
$\mathcal {L}$. Recall that we have defined ![]() $\mathcal {L}(L)$ in (2.6). Then the boundary of
$\mathcal {L}(L)$ in (2.6). Then the boundary of ![]() $\mathcal {L}(L)$ is the set
$\mathcal {L}(L)$ is the set
Recall we have the isomorphism ![]() $b:\mathbb {V}\rightarrow C$ defined in (2.3). Recall from [Reference Kudla and RapoportKR14a] or [Reference He, Shi and YangHSY23] that the vertices of
$b:\mathbb {V}\rightarrow C$ defined in (2.3). Recall from [Reference Kudla and RapoportKR14a] or [Reference He, Shi and YangHSY23] that the vertices of ![]() $\mathcal {L}_{2,1}$ correspond to vertex lattices of type
$\mathcal {L}_{2,1}$ correspond to vertex lattices of type ![]() $2$, and an edge corresponds to a vertex lattice of type
$2$, and an edge corresponds to a vertex lattice of type ![]() $0$. Each vertex of
$0$. Each vertex of ![]() $\mathcal {L}_{2,1}$ is contained in
$\mathcal {L}_{2,1}$ is contained in ![]() $q+1$ edges and each edge connects exactly two vertices. For
$q+1$ edges and each edge connects exactly two vertices. For ![]() ${\bf x}\in \mathbb {V}$ with
${\bf x}\in \mathbb {V}$ with ![]() $\mathrm {v}({\bf x})=0$ and
$\mathrm {v}({\bf x})=0$ and ![]() $\mathrm {Span}_F\{{\bf x}\}^{\perp }$ split, recall that
$\mathrm {Span}_F\{{\bf x}\}^{\perp }$ split, recall that ![]() $\mathcal {L}_{2,1}$ is the Bruhat–Tits tree of
$\mathcal {L}_{2,1}$ is the Bruhat–Tits tree of ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}^\mathrm {Pap}_{2,1}$. Then
$\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}^\mathrm {Pap}_{2,1}$. Then ![]() ${\bf x}$ determines an embedding
${\bf x}$ determines an embedding ![]() $\mathcal {L}_{2,1}\hookrightarrow \mathcal {L}$ defined as follows. First we send each vertex of
$\mathcal {L}_{2,1}\hookrightarrow \mathcal {L}$ defined as follows. First we send each vertex of ![]() $\mathcal {L}_{2,1}$ corresponding to a vertex lattice
$\mathcal {L}_{2,1}$ corresponding to a vertex lattice ![]() $\Lambda \subset \mathrm {Span}_F\{b({\bf x})\}^{\perp }$ of type
$\Lambda \subset \mathrm {Span}_F\{b({\bf x})\}^{\perp }$ of type ![]() $2$ to the vertex of
$2$ to the vertex of ![]() $\mathcal {L}$ corresponding to the type
$\mathcal {L}$ corresponding to the type ![]() $2$ lattice
$2$ lattice ![]() $\Lambda {\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$. An edge of
$\Lambda {\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$. An edge of ![]() $\mathcal {L}_{2,1}$ corresponding to a type
$\mathcal {L}_{2,1}$ corresponding to a type ![]() $0$ lattice
$0$ lattice ![]() $\Lambda _0\subset \mathrm {Span}_F\{b({\bf x})\}^{\perp }$ is broken into two pieces evenly and sent to the union of the two edges in
$\Lambda _0\subset \mathrm {Span}_F\{b({\bf x})\}^{\perp }$ is broken into two pieces evenly and sent to the union of the two edges in ![]() $\mathcal {L}$ joining the two vertices corresponding to
$\mathcal {L}$ joining the two vertices corresponding to ![]() $\Lambda {\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$ and
$\Lambda {\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$ and ![]() $\Lambda '{\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$ where
$\Lambda '{\unicode{x29BA}} \mathrm {Span} \{b({\bf x})\}$ where ![]() $\Lambda$ and
$\Lambda$ and ![]() $\Lambda '$ are the two type
$\Lambda '$ are the two type ![]() $2$ lattices containing
$2$ lattices containing ![]() $\Lambda _0$.
$\Lambda _0$.
9.2 Rank  $1$ case
$1$ case
Lemma 9.2 A point ![]() $z\in \mathcal {N}_3^\mathrm {Pap}(k)$ is in
$z\in \mathcal {N}_3^\mathrm {Pap}(k)$ is in ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if
$\mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if ![]() $b({\bf x})\in M(z)$.
$b({\bf x})\in M(z)$.
(1) Assume
 $\Lambda _0\in \mathcal {V}^0$, then the superspecial point
$\Lambda _0\in \mathcal {V}^0$, then the superspecial point  $\mathcal {N}_{\Lambda _0}(k)$ is in
$\mathcal {N}_{\Lambda _0}(k)$ is in  $\mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if
$\mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if  $b({\bf x})\in \Lambda _0$.
$b({\bf x})\in \Lambda _0$.(2) Assume
 $\Lambda _2\in \mathcal {V}^2$, then
$\Lambda _2\in \mathcal {V}^2$, then
 \[ \mathcal{Z}^\mathrm{Pap}({\bf x})(k) \cap \mathcal{N}_{\Lambda_2}(k)=\begin{cases} \mathcal{N}_{\Lambda_2}(k), & \text{if } b({\bf x}) \in \Lambda_2^\sharp, \\ \text{a superspecial point in } \mathcal{N}_{\Lambda_2}(k), & \text{if } b({\bf x})\in \Lambda_2 \backslash \Lambda_2^\sharp,\\ \emptyset, & \text{if } b({\bf x})\notin \Lambda_2. \end{cases} \]
\[ \mathcal{Z}^\mathrm{Pap}({\bf x})(k) \cap \mathcal{N}_{\Lambda_2}(k)=\begin{cases} \mathcal{N}_{\Lambda_2}(k), & \text{if } b({\bf x}) \in \Lambda_2^\sharp, \\ \text{a superspecial point in } \mathcal{N}_{\Lambda_2}(k), & \text{if } b({\bf x})\in \Lambda_2 \backslash \Lambda_2^\sharp,\\ \emptyset, & \text{if } b({\bf x})\notin \Lambda_2. \end{cases} \]
Proof. By Dieudonné theory, ![]() $z\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if
$z\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ if and only if ![]() ${\bf x}(M(\mathbb {Y}))\subset M(z)$ if and only if
${\bf x}(M(\mathbb {Y}))\subset M(z)$ if and only if ![]() $b({\bf x})\in M(z)$ since
$b({\bf x})\in M(z)$ since ![]() $e$ is a generator of
$e$ is a generator of ![]() $M(\mathbb {Y})$. For
$M(\mathbb {Y})$. For ![]() $z=\mathcal {N}_{\Lambda _0}(k)$ where
$z=\mathcal {N}_{\Lambda _0}(k)$ where ![]() $\Lambda _0\in \mathcal {V}^0$, we have
$\Lambda _0\in \mathcal {V}^0$, we have ![]() $M(z)=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$. Hence part (1) immediately follows.
$M(z)=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$. Hence part (1) immediately follows.
Now we proceed to prove part (2). If ![]() $b({\bf x})\in \Lambda ^\sharp$, then (9.2) tells us that
$b({\bf x})\in \Lambda ^\sharp$, then (9.2) tells us that ![]() $z\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ for any
$z\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$ for any ![]() $z\in \mathcal {N}^\circ _{\Lambda _2}(k)$. The fact that
$z\in \mathcal {N}^\circ _{\Lambda _2}(k)$. The fact that ![]() $\Lambda _2^\sharp \subset \Lambda _0$ for any
$\Lambda _2^\sharp \subset \Lambda _0$ for any ![]() $\Lambda _0\in \mathcal {L}^0$ contained in
$\Lambda _0\in \mathcal {L}^0$ contained in ![]() $\Lambda _2$ implies that
$\Lambda _2$ implies that ![]() $\mathcal {N}_{\Lambda _0}(k)\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$. Thus,
$\mathcal {N}_{\Lambda _0}(k)\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$. Thus, ![]() $\mathcal {N}_{\Lambda _2}(k)\subset \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$.
$\mathcal {N}_{\Lambda _2}(k)\subset \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$.
If ![]() $b({\bf x})\in \Lambda _2\backslash \Lambda _2^\sharp$, then
$b({\bf x})\in \Lambda _2\backslash \Lambda _2^\sharp$, then ![]() $\Lambda _0:= \Lambda ^\sharp +\mathrm {Span}\{b({\bf x})\}$ is a type
$\Lambda _0:= \Lambda ^\sharp +\mathrm {Span}\{b({\bf x})\}$ is a type ![]() $0$ lattice contained in
$0$ lattice contained in ![]() $\Lambda _2$ and
$\Lambda _2$ and ![]() $\mathcal {N}_{\Lambda _0}(k)\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$. On the other hand, since
$\mathcal {N}_{\Lambda _0}(k)\in \mathcal {Z}^\mathrm {Pap}({\bf x})(k)$. On the other hand, since ![]() $\tau (\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F})=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$, (9.2) tells us that
$\tau (\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F})=\Lambda _0\otimes _{\mathcal {O}_F} \mathcal {O}_{\breve F}$, (9.2) tells us that ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})$ does not contain any point in
$\mathcal {Z}^\mathrm {Pap}({\bf x})$ does not contain any point in ![]() $\mathcal {N}^\circ _{\Lambda _2}(k)$.
$\mathcal {N}^\circ _{\Lambda _2}(k)$.
If ![]() $b({\bf x})\notin \Lambda _2$, then
$b({\bf x})\notin \Lambda _2$, then ![]() $b({\bf x})\notin M(z)$ for any
$b({\bf x})\notin M(z)$ for any ![]() $z\in \mathcal {N}_{\Lambda _2}(k)$, hence
$z\in \mathcal {N}_{\Lambda _2}(k)$, hence ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})(k) \cap \mathcal {N}_{\Lambda _2}(k)=\emptyset$.
$\mathcal {Z}^\mathrm {Pap}({\bf x})(k) \cap \mathcal {N}_{\Lambda _2}(k)=\emptyset$.
Corollary 9.3 Let ![]() $L \subset \mathbb {V}$. Assume
$L \subset \mathbb {V}$. Assume ![]() $z\in \mathcal {Z}^\mathrm {Pap}(L)(k)$ and
$z\in \mathcal {Z}^\mathrm {Pap}(L)(k)$ and ![]() $z \in \mathcal {N}_{\Lambda }(k)$ where
$z \in \mathcal {N}_{\Lambda }(k)$ where ![]() $\Lambda \in \mathcal {V}^2$. Then
$\Lambda \in \mathcal {V}^2$. Then ![]() $\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}(\pi L).$
$\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}(\pi L).$
Corollary 9.4 Assume ![]() ${\bf x} \in \mathbb {V}$ and
${\bf x} \in \mathbb {V}$ and ![]() $\mathrm {v}({\bf x})>0$. Assume
$\mathrm {v}({\bf x})>0$. Assume ![]() $\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}({\bf x})_{\mathrm {red}}$ where
$\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}({\bf x})_{\mathrm {red}}$ where ![]() $\Lambda \in \mathcal {V}^2$, then either
$\Lambda \in \mathcal {V}^2$, then either ![]() $\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}(({1}/{\pi }){\bf x})_{\mathrm {red}}$ or
$\mathcal {N}_{\Lambda }\subset \mathcal {Z}^\mathrm {Pap}(({1}/{\pi }){\bf x})_{\mathrm {red}}$ or ![]() $\mathcal {N}_{\Lambda }\cap \mathcal {Z}^\mathrm {Pap}(({1}/{\pi }){\bf x})_{\mathrm {red}}$ is a unique superspecial point.
$\mathcal {N}_{\Lambda }\cap \mathcal {Z}^\mathrm {Pap}(({1}/{\pi }){\bf x})_{\mathrm {red}}$ is a unique superspecial point.
Lemma 9.5 For ![]() $L\subset \mathbb {V}$ a lattice of arbitrary rank,
$L\subset \mathbb {V}$ a lattice of arbitrary rank, ![]() $\mathcal {Z}^\mathrm {Pap}(L)_{\mathrm {red}}$ is connected.
$\mathcal {Z}^\mathrm {Pap}(L)_{\mathrm {red}}$ is connected.
Proof. Suppose ![]() $\mathcal {Z}^\mathrm {Pap}(L)_{\mathrm {red}}$ has two different connected components
$\mathcal {Z}^\mathrm {Pap}(L)_{\mathrm {red}}$ has two different connected components ![]() $U_1$ and
$U_1$ and ![]() $U_2$. Since
$U_2$. Since ![]() $\mathrm {SU}(\mathbb {V})$ acts transitively on
$\mathrm {SU}(\mathbb {V})$ acts transitively on ![]() $\mathcal {L}$, we can find a
$\mathcal {L}$, we can find a ![]() ${\bf x}\in \mathbb {V}$ such that
${\bf x}\in \mathbb {V}$ such that ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}^\mathrm {Pap}_{2,1}$ (i.e.
$\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}^\mathrm {Pap}_{2,1}$ (i.e. ![]() $\{{\bf x}\}^\bot$ is split) and
$\{{\bf x}\}^\bot$ is split) and ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})_{\mathrm {red}}\cap U_i\neq \emptyset$ for
$\mathcal {Z}^\mathrm {Pap}({\bf x})_{\mathrm {red}}\cap U_i\neq \emptyset$ for ![]() $i=1,2$. Hence, the reduced locus of
$i=1,2$. Hence, the reduced locus of
is not connected where ![]() $L'$ is the orthogonal projection of
$L'$ is the orthogonal projection of ![]() $L$ onto
$L$ onto ![]() $\{{\bf x}\}^\bot$. This contradicts Corollaries 3.13 and 3.15 and Lemma 3.16 of [Reference He, Shi and YangHSY23].
$\{{\bf x}\}^\bot$. This contradicts Corollaries 3.13 and 3.15 and Lemma 3.16 of [Reference He, Shi and YangHSY23].
Recall that for a lattice ![]() $L\subset \mathbb {V}$ (respectively,
$L\subset \mathbb {V}$ (respectively, ![]() ${\bf x}\in \mathbb {V}$), we have defined
${\bf x}\in \mathbb {V}$), we have defined ![]() $\mathcal {V}(L)$ and
$\mathcal {V}(L)$ and ![]() $\mathcal {L}(L)$ (respectively,
$\mathcal {L}(L)$ (respectively, ![]() $\mathcal {V}({\bf x})$ and
$\mathcal {V}({\bf x})$ and ![]() $\mathcal {L}({\bf x})$) in § 2.3.
$\mathcal {L}({\bf x})$) in § 2.3.
Proposition 9.6 Assume that ![]() ${\bf x}\in \mathbb {V}$ such that
${\bf x}\in \mathbb {V}$ such that ![]() $h({\bf x},{\bf x})\neq 0$. Then we have
$h({\bf x},{\bf x})\neq 0$. Then we have
where ![]() $\mathcal {V}({\bf x})$ is given as follows.
$\mathcal {V}({\bf x})$ is given as follows.
(1) When
 $\mathrm {v}({\bf x})=0$ and
$\mathrm {v}({\bf x})=0$ and  $\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is non-split, there is a unique vertex lattice
$\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is non-split, there is a unique vertex lattice  $\Lambda _{\bf x}\in \mathcal {V}^0$ containing
$\Lambda _{\bf x}\in \mathcal {V}^0$ containing  $b({\bf x})$. In this case
$b({\bf x})$. In this case  $\mathcal {V}({\bf x})=\{\Lambda _{\bf x}\}$.
$\mathcal {V}({\bf x})=\{\Lambda _{\bf x}\}$.(2) When
 $\mathrm {v}({\bf x})=d$ and
$\mathrm {v}({\bf x})=d$ and  $\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is non-split, we have
where
$\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is non-split, we have
where \[ \mathcal{V}({\bf x})=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \Lambda_{{\bf x}/\pi^d})\le d \} \]
\[ \mathcal{V}({\bf x})=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \Lambda_{{\bf x}/\pi^d})\le d \} \]
 $\Lambda _{{\bf x}/\pi ^d}$ is as in part (1).
$\Lambda _{{\bf x}/\pi ^d}$ is as in part (1).(3) When
 $\mathrm {v}({\bf x})=0$ and
$\mathrm {v}({\bf x})=0$ and  $\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is split,
$\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is split,  $\mathcal {L}({\bf x})$ is the tree
$\mathcal {L}({\bf x})$ is the tree  $\mathcal {L}_{2,1}$.
$\mathcal {L}_{2,1}$.(4) When
 $\mathrm {v}({\bf x})=d$ and
$\mathrm {v}({\bf x})=d$ and  $\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is split, we have
where
$\mathrm {Span}_F\{{\bf x}\}^{\perp }$ is split, we have
where \[ \mathcal{V}({\bf x})=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \mathcal{L}({\bf x}/\pi^d))\le d \} \]
\[ \mathcal{V}({\bf x})=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \mathcal{L}({\bf x}/\pi^d))\le d \} \]
 $\mathcal {L}({\bf x}/\pi ^d)$ is as in part (3).
$\mathcal {L}({\bf x}/\pi ^d)$ is as in part (3).(5) When
 $h({\bf x}, {\bf x}) \notin \mathcal {O}_{F_0}$,
$h({\bf x}, {\bf x}) \notin \mathcal {O}_{F_0}$,  $\mathcal {V}({\bf x})$ is empty.
$\mathcal {V}({\bf x})$ is empty.
Proof. Proof of part (1). This is a direct consequence of Proposition 2.6 and the fact that ![]() $\mathcal {N}_{2,-1}^\mathrm {Pap}$ has only one reduced point, see [Reference ShiShi22, § 2] or [Reference Rapoport, Smithling and ZhangRSZ18, § 8]. Alternatively since
$\mathcal {N}_{2,-1}^\mathrm {Pap}$ has only one reduced point, see [Reference ShiShi22, § 2] or [Reference Rapoport, Smithling and ZhangRSZ18, § 8]. Alternatively since ![]() $\mathrm {Span}_F\{b({\bf x})\}^{\perp }$ is non-split of dimension
$\mathrm {Span}_F\{b({\bf x})\}^{\perp }$ is non-split of dimension ![]() $2$, it contains a unique self-dual lattice
$2$, it contains a unique self-dual lattice ![]() $\Lambda '$, then
$\Lambda '$, then ![]() $\Lambda _{\bf x}:= \mathrm {Span}\{b({\bf x})\}\oplus \Lambda '$ is the unique type
$\Lambda _{\bf x}:= \mathrm {Span}\{b({\bf x})\}\oplus \Lambda '$ is the unique type ![]() $0$ lattice containing
$0$ lattice containing ![]() $b({\bf x})$.
$b({\bf x})$.
Proof of part (3). Applying Proposition 2.6,we see that ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}_{2,1}^\mathrm {Pap}$ is the Drinfeld
$\mathcal {Z}^\mathrm {Pap}({\bf x})\cong \mathcal {N}_{2,1}^\mathrm {Pap}$ is the Drinfeld ![]() $p$-adic half space, see [Reference Kudla and RapoportKR14a] and [Reference He, Shi and YangHSY23]. The required properties of
$p$-adic half space, see [Reference Kudla and RapoportKR14a] and [Reference He, Shi and YangHSY23]. The required properties of ![]() $\mathcal {L}({\bf x})$ and
$\mathcal {L}({\bf x})$ and ![]() $\mathcal {V}({\bf x})$ follow.
$\mathcal {V}({\bf x})$ follow.
Proof of part (2). We prove this by induction. The case ![]() $d=0$ is just part (1). Now we assume
$d=0$ is just part (1). Now we assume ![]() $d>0$ and that the statement holds for
$d>0$ and that the statement holds for ![]() $d-1$, i.e.
$d-1$, i.e.
Then applying Corollary 9.3 to the lattice ![]() $L=\mathrm {Span}\{{\bf x}/\pi \}$ we have
$L=\mathrm {Span}\{{\bf x}/\pi \}$ we have
Corollary 9.4 and the induction hypothesis imply that every ![]() $\Lambda _2\in \mathcal {V}^2({\bf x})$ satisfies
$\Lambda _2\in \mathcal {V}^2({\bf x})$ satisfies ![]() $d(\Lambda, \Lambda _{{\bf x}/\pi ^d}) \le d$. By Lemma 9.5 there is no isolated
$d(\Lambda, \Lambda _{{\bf x}/\pi ^d}) \le d$. By Lemma 9.5 there is no isolated ![]() $\Lambda _0\in \mathcal {V}^0({\bf x})$, i.e. every
$\Lambda _0\in \mathcal {V}^0({\bf x})$, i.e. every ![]() $\Lambda _0\in \mathcal {V}^0({\bf x})$ is contained in some
$\Lambda _0\in \mathcal {V}^0({\bf x})$ is contained in some ![]() $\Lambda _2\in \mathcal {V}^2({\bf x})$ if
$\Lambda _2\in \mathcal {V}^2({\bf x})$ if ![]() $\mathrm {v}({\bf x})>0$. This finishes the proof of part (2).
$\mathrm {v}({\bf x})>0$. This finishes the proof of part (2).
Similarly we can prove part (4) by an induction on ![]() $d$, the case
$d$, the case ![]() $d=0$ is just part (3).
$d=0$ is just part (3).
Part (5) follows directly from Lemma 9.2.
9.3 Rank  $2$ case
$2$ case
Proposition 9.7 Assume that ![]() $L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}\subset \mathbb {V}$ is integral of rank
$L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}\subset \mathbb {V}$ is integral of rank ![]() $2$. Then
$2$. Then
is a finite union, where ![]() $\mathcal {V}(L^\flat )$ is the set of vertices of the tree
$\mathcal {V}(L^\flat )$ is the set of vertices of the tree ![]() $\mathcal {L}(L^\flat )$ described as follows.
$\mathcal {L}(L^\flat )$ described as follows.
(1) Assume
 $L^\flat \approx \mathcal {H}_{2a+1}$ for some
$L^\flat \approx \mathcal {H}_{2a+1}$ for some  $a\in \mathbb {Z}_{\ge 0}$. Then
$a\in \mathbb {Z}_{\ge 0}$. Then  $\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type
$\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type  $2$ with radius
$2$ with radius  $({2a+1})/{2}$.
$({2a+1})/{2}$.(2) Assume
 $L^\flat =\mathrm {Span}\{\pi ^a{\bf x}_1,\pi ^a{\bf x}_2\}$ where
$L^\flat =\mathrm {Span}\{\pi ^a{\bf x}_1,\pi ^a{\bf x}_2\}$ where  $\mathrm {v}({\bf x}_1)=0$,
$\mathrm {v}({\bf x}_1)=0$,  $\mathrm {v}({\bf x}_2)\geq 0$ and
$\mathrm {v}({\bf x}_2)\geq 0$ and  $\mathrm {Span}_F\{{\bf x}_1\}^\bot$ is non-split. Then
$\mathrm {Span}_F\{{\bf x}_1\}^\bot$ is non-split. Then  $\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type
$\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type  $0$ with radius
$0$ with radius  $a$.
$a$.(3) Assume
 $L^\flat =\mathrm {Span}\{\pi ^a{\bf x}_1,\pi ^{a+r}{\bf x}_2\}$ where
$L^\flat =\mathrm {Span}\{\pi ^a{\bf x}_1,\pi ^{a+r}{\bf x}_2\}$ where  ${\bf x}_1\bot {\bf x}_2$,
${\bf x}_1\bot {\bf x}_2$,  $\mathrm {v}({\bf x}_1)=\mathrm {v}({\bf x}_2)=0$,
$\mathrm {v}({\bf x}_1)=\mathrm {v}({\bf x}_2)=0$,  $r\geq 0$ and
$r\geq 0$ and  $\mathrm {Span}_F\{{\bf x}_1\}^\bot$ is split. Then
where
$\mathrm {Span}_F\{{\bf x}_1\}^\bot$ is split. Then
where \[ \mathcal{L}(L^\flat)=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \mathcal{L}(\pi^{-a}L^\flat))\le a\}, \]
\[ \mathcal{L}(L^\flat)=\{\Lambda\in \mathcal{V}\mid d(\Lambda, \mathcal{L}(\pi^{-a}L^\flat))\le a\}, \]
 \[ \mathcal{L}(\pi^{-a}L^\flat)=\{\Lambda\in \mathcal{L}({\bf x}_1)\mid d(\Lambda, \Lambda_0)\le r\}, \]
\[ \mathcal{L}(\pi^{-a}L^\flat)=\{\Lambda\in \mathcal{L}({\bf x}_1)\mid d(\Lambda, \Lambda_0)\le r\}, \]
 $\mathcal {L}({\bf x}_1)$ is described in part (3) of Proposition 9.6 and
$\mathcal {L}({\bf x}_1)$ is described in part (3) of Proposition 9.6 and  $\Lambda _0$ is the unique type
$\Lambda _0$ is the unique type  $0$ vertex lattice containing
$0$ vertex lattice containing  $\{{\bf x}_1,{\bf x}_2\}$.
$\{{\bf x}_1,{\bf x}_2\}$.
Proof. As in the proof of Proposition 9.2, for a ![]() $\Lambda \in \mathcal {V}$,
$\Lambda \in \mathcal {V}$, ![]() $\mathcal {N}_\Lambda \subset \mathcal {Z}^\mathrm {Pap}(L^\flat )_{\mathrm {red}}$ if and only if
$\mathcal {N}_\Lambda \subset \mathcal {Z}^\mathrm {Pap}(L^\flat )_{\mathrm {red}}$ if and only if ![]() $\Lambda ^\sharp$ contains
$\Lambda ^\sharp$ contains ![]() $b({\bf x}_1),b({\bf x}_2)$.
$b({\bf x}_1),b({\bf x}_2)$.
We first prove part (1) when ![]() $a=0$. Suppose
$a=0$. Suppose ![]() $\Lambda \in \mathcal {V}^2(L^\flat )$. Extend
$\Lambda \in \mathcal {V}^2(L^\flat )$. Extend ![]() $\{b({\bf x}_1),b({\bf x}_2)\}$ to a basis
$\{b({\bf x}_1),b({\bf x}_2)\}$ to a basis ![]() $\{b({\bf x}_1),b({\bf x}_2),b_3\}$ of
$\{b({\bf x}_1),b({\bf x}_2),b_3\}$ of ![]() $\mathbb {V}$ with Gram matrix
$\mathbb {V}$ with Gram matrix ![]() $\mathcal {H}_1\oplus \{-\epsilon \}$. Choose a basis
$\mathcal {H}_1\oplus \{-\epsilon \}$. Choose a basis ![]() $\{v_1,v_2,v_3\}$ of
$\{v_1,v_2,v_3\}$ of ![]() $\Lambda ^\sharp$ with the same Gram matrix
$\Lambda ^\sharp$ with the same Gram matrix ![]() $\mathcal {H}_1\oplus \{-\epsilon \}$. Then
$\mathcal {H}_1\oplus \{-\epsilon \}$. Then ![]() $b({\bf x}_i) \in \Lambda ^\sharp$ (
$b({\bf x}_i) \in \Lambda ^\sharp$ (![]() $i=1,2$) by Lemma 9.2 and
$i=1,2$) by Lemma 9.2 and
where ![]() $a_{ij} \in \mathcal {O}_F$ (
$a_{ij} \in \mathcal {O}_F$ (![]() $j=1,2,3$). The fact that
$j=1,2,3$). The fact that ![]() $(b({\bf x}_i),b({\bf x}_j))_{1\leq i,j \leq 2}=T$ implies
$(b({\bf x}_i),b({\bf x}_j))_{1\leq i,j \leq 2}=T$ implies ![]() $a_{i3}\in \pi \mathcal {O}_F$ for
$a_{i3}\in \pi \mathcal {O}_F$ for ![]() $i=1,2$ and
$i=1,2$ and ![]() $(a_{ij})_{1\leq i,j \leq 2}$ is in
$(a_{ij})_{1\leq i,j \leq 2}$ is in ![]() $\mathrm {GL}_2(\mathcal {O}_F)$. This guarantees that
$\mathrm {GL}_2(\mathcal {O}_F)$. This guarantees that ![]() $L^\flat$ is a direct summand of
$L^\flat$ is a direct summand of ![]() $\Lambda ^\sharp$ by the Gram–Schmidt process. Hence,
$\Lambda ^\sharp$ by the Gram–Schmidt process. Hence, ![]() $\Lambda ^\sharp$ is, in fact, the lattice
$\Lambda ^\sharp$ is, in fact, the lattice ![]() $\mathrm {Span}_{\mathcal {O}_F}\{b({\bf x}_1),b({\bf x}_2),b_3\}$. The fact that all
$\mathrm {Span}_{\mathcal {O}_F}\{b({\bf x}_1),b({\bf x}_2),b_3\}$. The fact that all ![]() $\Lambda _0\in \mathcal {V}^0(L^\flat )$ are in
$\Lambda _0\in \mathcal {V}^0(L^\flat )$ are in ![]() $\Lambda$ follows from Lemma 9.5.
$\Lambda$ follows from Lemma 9.5.
When ![]() $a=0$, part (2) follows from the fact that
$a=0$, part (2) follows from the fact that ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x}_1)=\mathcal {N}^\mathrm {Pap}_{2,-1}$ (by Proposition 2.6) and
$\mathcal {Z}^\mathrm {Pap}({\bf x}_1)=\mathcal {N}^\mathrm {Pap}_{2,-1}$ (by Proposition 2.6) and ![]() $\mathcal {Z}^\mathrm {Pap}(L^\flat )_{\mathrm {red}}=\mathcal {Z}^\mathrm {Pap}({\bf x}_1)_{\mathrm {red}}$ is a unique superspecial point. Similarly when
$\mathcal {Z}^\mathrm {Pap}(L^\flat )_{\mathrm {red}}=\mathcal {Z}^\mathrm {Pap}({\bf x}_1)_{\mathrm {red}}$ is a unique superspecial point. Similarly when ![]() $a=0$, (3) follows from the fact that
$a=0$, (3) follows from the fact that ![]() $\mathcal {Z}^\mathrm {Pap}({\bf x}_1)=\mathcal {N}^\mathrm {Pap}_{2,1}$ and [Reference He, Shi and YangHSY23, Corollary 3.13].
$\mathcal {Z}^\mathrm {Pap}({\bf x}_1)=\mathcal {N}^\mathrm {Pap}_{2,1}$ and [Reference He, Shi and YangHSY23, Corollary 3.13].
Now we prove parts (1), (2) and (3) for general ![]() $a$. First,
$a$. First, ![]() $\mathcal {L}(L^\flat )=\mathcal {L}(\pi ^a{\bf x}_1)\cap \mathcal {L}(\pi ^a{\bf x}_2)$ by definition. By Corollary 9.3 we have
$\mathcal {L}(L^\flat )=\mathcal {L}(\pi ^a{\bf x}_1)\cap \mathcal {L}(\pi ^a{\bf x}_2)$ by definition. By Corollary 9.3 we have
Note that for a sub-tree ![]() $\mathcal {L}'$ of a tree
$\mathcal {L}'$ of a tree ![]() $\mathcal {L}$ and a vertex
$\mathcal {L}$ and a vertex ![]() $x\in \mathcal {L}\setminus \mathcal {L}'$, there is a unique geodesic segment joining
$x\in \mathcal {L}\setminus \mathcal {L}'$, there is a unique geodesic segment joining ![]() $x$ with
$x$ with ![]() $\mathcal {L}'$. Given
$\mathcal {L}'$. Given ![]() $\Lambda \in \mathcal {L}(L^\flat )=\mathcal {L}(\pi ^a {\bf x}_1)\cap \mathcal {L}(\pi ^a {\bf x}_2)$, let
$\Lambda \in \mathcal {L}(L^\flat )=\mathcal {L}(\pi ^a {\bf x}_1)\cap \mathcal {L}(\pi ^a {\bf x}_2)$, let ![]() $\gamma$ be the unique geodesic segment joining
$\gamma$ be the unique geodesic segment joining ![]() $\Lambda$ with
$\Lambda$ with ![]() $\mathcal {L}(\pi ^{-a} L^\flat )$. Assume that
$\mathcal {L}(\pi ^{-a} L^\flat )$. Assume that ![]() $\gamma$ intersects
$\gamma$ intersects ![]() $\mathcal {L}(\pi ^{-a}L^\flat )$ at
$\mathcal {L}(\pi ^{-a}L^\flat )$ at ![]() $\Lambda (L^\flat )$. Since
$\Lambda (L^\flat )$. Since ![]() $\mathcal {L}(\pi ^{-a} L^\flat )=\mathcal {L}({\bf x}_1)\cap \mathcal {L}({\bf x}_2)$,
$\mathcal {L}(\pi ^{-a} L^\flat )=\mathcal {L}({\bf x}_1)\cap \mathcal {L}({\bf x}_2)$, ![]() $\gamma$ necessarily intersects both
$\gamma$ necessarily intersects both ![]() $\mathcal {L}({\bf x}_1)$ and
$\mathcal {L}({\bf x}_1)$ and ![]() $\mathcal {L}({\bf x}_2)$. Without loss of generality we assume that
$\mathcal {L}({\bf x}_2)$. Without loss of generality we assume that ![]() $\gamma$ intersects
$\gamma$ intersects ![]() $\mathcal {L}({\bf x}_1)$ at
$\mathcal {L}({\bf x}_1)$ at ![]() $\Lambda ({\bf x}_1)$ first. Hence, the intersection of
$\Lambda ({\bf x}_1)$ first. Hence, the intersection of ![]() $\gamma$ with
$\gamma$ with ![]() $\mathcal {L}({\bf x}_2)$ is
$\mathcal {L}({\bf x}_2)$ is ![]() $\Lambda (L^\flat )$ and
$\Lambda (L^\flat )$ and
Now by Proposition 9.6, we have
Hence, ![]() $d(\Lambda,\mathcal {L}(\pi ^{-a}L^\flat ))\leq a$. This shows that
$d(\Lambda,\mathcal {L}(\pi ^{-a}L^\flat ))\leq a$. This shows that
The general case of parts (1), (2) and (3) follows from the above equation and the case ![]() $a=0$.
$a=0$.
Note that parts (1), (2) and (3) have covered all possibilities of ![]() $L^\flat$ due to the classification of Hermitian lattices. Note that in every case
$L^\flat$ due to the classification of Hermitian lattices. Note that in every case ![]() $\mathcal {V}(L^\flat )$ is finite. This finishes the proof of the proposition.
$\mathcal {V}(L^\flat )$ is finite. This finishes the proof of the proposition.
Definition 9.8 Assume that ![]() $L^\flat$ is an integral lattice of rank
$L^\flat$ is an integral lattice of rank ![]() $2$ in
$2$ in ![]() $\mathbb {V}$. Define
$\mathbb {V}$. Define ![]() $\mathcal {S}(L^\flat )$, the skeleton of
$\mathcal {S}(L^\flat )$, the skeleton of ![]() $\mathcal {L}(L^\flat )$, as follows. If the fundamental invariant of
$\mathcal {L}(L^\flat )$, as follows. If the fundamental invariant of ![]() $L^\flat$ is
$L^\flat$ is ![]() $(2a,b)$ (
$(2a,b)$ (![]() $b\geq 2a$), define
$b\geq 2a$), define ![]() $\mathcal {S}(L^\flat ):= \mathcal {L}(\pi ^{-a}L^\flat )$. If the fundamental invariant of
$\mathcal {S}(L^\flat ):= \mathcal {L}(\pi ^{-a}L^\flat )$. If the fundamental invariant of ![]() $L^\flat$ is
$L^\flat$ is ![]() $(2a+1,2a+1)$, define
$(2a+1,2a+1)$, define ![]() $\mathcal {S}(L^\flat ):= \emptyset$.
$\mathcal {S}(L^\flat ):= \emptyset$.
Remark 9.9 The skeleton ![]() $\mathcal {S}(L^\flat )$ is isomorphic to a ball in the Bruhat–Tits tree of
$\mathcal {S}(L^\flat )$ is isomorphic to a ball in the Bruhat–Tits tree of ![]() $\mathcal {N}^\mathrm {Pap}_{2,\pm 1}$.
$\mathcal {N}^\mathrm {Pap}_{2,\pm 1}$.
Corollary 9.10 For each ![]() $\Lambda _2\in \mathcal {V}^2(L^\flat )$ not on the skeleton
$\Lambda _2\in \mathcal {V}^2(L^\flat )$ not on the skeleton ![]() $\mathcal {S}(L^\flat )$, one can find
$\mathcal {S}(L^\flat )$, one can find ![]() $\Lambda _0\in \mathcal {V}^0(L^\flat )$ such that
$\Lambda _0\in \mathcal {V}^0(L^\flat )$ such that ![]() $\Lambda _2$ has the largest distance to the boundary
$\Lambda _2$ has the largest distance to the boundary ![]() $\mathcal {B}(L^\flat )$ of
$\mathcal {B}(L^\flat )$ of ![]() $\mathcal {L}(L^\flat )$ among all type
$\mathcal {L}(L^\flat )$ among all type ![]() $2$ lattices in
$2$ lattices in ![]() $\mathcal {V}^2(L^\flat )$ containing
$\mathcal {V}^2(L^\flat )$ containing ![]() $\Lambda _0$.
$\Lambda _0$.
Proof. Assume the fundamental invariant of ![]() $L^\flat$ is
$L^\flat$ is ![]() $(2a,b)$ or
$(2a,b)$ or ![]() $(2a+1,2a+1)$. Define
$(2a+1,2a+1)$. Define ![]() $M^\flat := \pi ^{-a}L^\flat$. Let
$M^\flat := \pi ^{-a}L^\flat$. Let ![]() $b$ be the unique integer such that
$b$ be the unique integer such that ![]() $\Lambda _2\in \mathcal {L}(\pi ^b M^\flat )\setminus \mathcal {L}(\pi ^{b-1} M^\flat )$. Choose any
$\Lambda _2\in \mathcal {L}(\pi ^b M^\flat )\setminus \mathcal {L}(\pi ^{b-1} M^\flat )$. Choose any ![]() $\Lambda _0\in \mathcal {B}(\pi ^b M^\flat )$ such that
$\Lambda _0\in \mathcal {B}(\pi ^b M^\flat )$ such that ![]() $\Lambda _0\subset \Lambda$. Then by Proposition 9.7,
$\Lambda _0\subset \Lambda$. Then by Proposition 9.7, ![]() $\Lambda _0$ satisfies the assumption of the corollary.
$\Lambda _0$ satisfies the assumption of the corollary.
9.4 The Krämer model
For ![]() $\Lambda \in \mathcal {V}^2$, let
$\Lambda \in \mathcal {V}^2$, let ![]() $\tilde {\mathcal {N}}_\Lambda$ be the strict transform of
$\tilde {\mathcal {N}}_\Lambda$ be the strict transform of ![]() $\mathcal {N}_\Lambda$ under the blow-up
$\mathcal {N}_\Lambda$ under the blow-up ![]() $\mathcal {N}^\mathrm {Kra}\rightarrow \mathcal {N}^\mathrm {Pap}$. Since the strict transform of a regular curve along any of its closed point is an isomorphism, we know
$\mathcal {N}^\mathrm {Kra}\rightarrow \mathcal {N}^\mathrm {Pap}$. Since the strict transform of a regular curve along any of its closed point is an isomorphism, we know ![]() $\tilde {\mathcal {N}}_\Lambda \cong \mathbb {P}^1$.
$\tilde {\mathcal {N}}_\Lambda \cong \mathbb {P}^1$.
Lemma 9.11 For ![]() $\Lambda \ne \Lambda '\in \mathcal {V}^2$,
$\Lambda \ne \Lambda '\in \mathcal {V}^2$, ![]() $\tilde {\mathcal {N}}_\Lambda$ and
$\tilde {\mathcal {N}}_\Lambda$ and ![]() $\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect.
$\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect.
Proof. If ![]() $\mathcal {N}_{\Lambda }$ and
$\mathcal {N}_{\Lambda }$ and ![]() $\mathcal {N}_{\Lambda '}$ do not intersect in
$\mathcal {N}_{\Lambda '}$ do not intersect in ![]() $\mathcal {N}^\mathrm {Pap}$, then obviously
$\mathcal {N}^\mathrm {Pap}$, then obviously ![]() $\tilde {\mathcal {N}}_\Lambda$ and
$\tilde {\mathcal {N}}_\Lambda$ and ![]() $\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect. Without loss of generality we can assume
$\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect. Without loss of generality we can assume ![]() $\Lambda =\mathrm {Span}\{e_1,e_2,e_3\}$ and
$\Lambda =\mathrm {Span}\{e_1,e_2,e_3\}$ and ![]() $\Lambda '=\mathrm {Span}\{\pi ^{-1}e_1,\pi e_2,e_3\}$ where the Gram matrix of
$\Lambda '=\mathrm {Span}\{\pi ^{-1}e_1,\pi e_2,e_3\}$ where the Gram matrix of ![]() $\{e_1,e_2,e_3\}$ is
$\{e_1,e_2,e_3\}$ is ![]() $\mathrm {Diag}(\mathcal {H}, \epsilon )$. Take
$\mathrm {Diag}(\mathcal {H}, \epsilon )$. Take ![]() ${\bf x}_0=e_3$. Then by Proposition 9.7, both
${\bf x}_0=e_3$. Then by Proposition 9.7, both ![]() $\tilde {\mathcal {N}}_{\Lambda }$ and
$\tilde {\mathcal {N}}_{\Lambda }$ and ![]() $\tilde {\mathcal {N}}_{\Lambda '}$ are in
$\tilde {\mathcal {N}}_{\Lambda '}$ are in ![]() $\tilde {\mathcal {Z}}({\bf x}_0)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$. Now by [Reference He, Shi and YangHSY23, Lemma 5.3],
$\tilde {\mathcal {Z}}({\bf x}_0)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$. Now by [Reference He, Shi and YangHSY23, Lemma 5.3], ![]() $\tilde {\mathcal {N}}_{\Lambda }$ and
$\tilde {\mathcal {N}}_{\Lambda }$ and ![]() $\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect.
$\tilde {\mathcal {N}}_{\Lambda '}$ do not intersect.
Lemma 9.12 Let ![]() $\Lambda \in \mathcal {V}^2$ and
$\Lambda \in \mathcal {V}^2$ and ![]() $\Lambda _0\in \mathcal {V}^0$. When
$\Lambda _0\in \mathcal {V}^0$. When ![]() $\Lambda _0 \subset \Lambda$,
$\Lambda _0 \subset \Lambda$, ![]() $\tilde {\mathcal {N}}_\Lambda$ intersects properly with
$\tilde {\mathcal {N}}_\Lambda$ intersects properly with ![]() $\mathrm {Exc}_{\Lambda _0}$ and
$\mathrm {Exc}_{\Lambda _0}$ and
When ![]() $\Lambda _0$ is not contained in
$\Lambda _0$ is not contained in ![]() $\Lambda$,
$\Lambda$, ![]() $\tilde {\mathcal {N}}_\Lambda$ does not intersect with
$\tilde {\mathcal {N}}_\Lambda$ does not intersect with ![]() $\mathrm {Exc}_{\Lambda _0}$.
$\mathrm {Exc}_{\Lambda _0}$.
Proof. First assume ![]() $\Lambda _0\subset \Lambda$. Since
$\Lambda _0\subset \Lambda$. Since ![]() $\tilde {\mathcal {N}}_\Lambda$ is a strict transformation of a curve, it intersects the exceptional divisor properly. Let
$\tilde {\mathcal {N}}_\Lambda$ is a strict transformation of a curve, it intersects the exceptional divisor properly. Let ![]() ${\bf x}_0$ be as in the proof of Lemma 9.11. Then
${\bf x}_0$ be as in the proof of Lemma 9.11. Then ![]() $\tilde {\mathcal {N}}_{\Lambda }$ is in
$\tilde {\mathcal {N}}_{\Lambda }$ is in ![]() $\tilde {\mathcal {Z}}({\bf x}_0)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$:
$\tilde {\mathcal {Z}}({\bf x}_0)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$:
 \begin{align*} \chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}) &=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes_{\mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}} \mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}\otimes\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}})\\ &=\chi(\tilde{\mathcal{Z}}({\bf x}_0),\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes_{\mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}} \mathcal{O}_{\mathrm{Exc}'}). \end{align*}
\begin{align*} \chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}) &=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes_{\mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}} \mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}\otimes\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}})\\ &=\chi(\tilde{\mathcal{Z}}({\bf x}_0),\mathcal{O}_{\tilde{\mathcal{N}}_\Lambda}\otimes_{\mathcal{O}_{\tilde{\mathcal{Z}}({\bf x}_0)}} \mathcal{O}_{\mathrm{Exc}'}). \end{align*}
Here ![]() $\mathrm {Exc}'\cong \mathbb {P}^1_k$ is the exceptional divisor on
$\mathrm {Exc}'\cong \mathbb {P}^1_k$ is the exceptional divisor on ![]() $\tilde {\mathcal {Z}}({\bf x}_0)$ corresponding to the rank
$\tilde {\mathcal {Z}}({\bf x}_0)$ corresponding to the rank ![]() $2$ self-dual lattice
$2$ self-dual lattice
By [Reference He, Shi and YangHSY23, Lemma 5.2(a)], we know ![]() $\chi (\tilde {\mathcal {Z}}({\bf x}_0),\mathcal {O}_{\tilde {\mathcal {N}}_\Lambda }\otimes _{\mathcal {O}_{\tilde {\mathcal {Z}}({\bf x}_0)}} \mathcal {O}_{\mathrm {Exc}'})=1$. When
$\chi (\tilde {\mathcal {Z}}({\bf x}_0),\mathcal {O}_{\tilde {\mathcal {N}}_\Lambda }\otimes _{\mathcal {O}_{\tilde {\mathcal {Z}}({\bf x}_0)}} \mathcal {O}_{\mathrm {Exc}'})=1$. When ![]() $\Lambda _0$ is not contained in
$\Lambda _0$ is not contained in ![]() $\Lambda$, the superspecial point
$\Lambda$, the superspecial point ![]() $\mathcal {N}_{\Lambda _0}(k)$ is not contained in
$\mathcal {N}_{\Lambda _0}(k)$ is not contained in ![]() $\mathcal {N}_\Lambda$, hence
$\mathcal {N}_\Lambda$, hence ![]() $\tilde {\mathcal {N}}_\Lambda$ does not intersect with
$\tilde {\mathcal {N}}_\Lambda$ does not intersect with ![]() $\mathrm {Exc}_{\Lambda _0}$.
$\mathrm {Exc}_{\Lambda _0}$.
10. Intersection of vertical components and special divisors
In this section we study the intersection of ![]() $\tilde {\mathcal {N}}_{\Lambda }$ and special divisors. The main result is Theorem 10.2. To proceed we first study the decomposition of
$\tilde {\mathcal {N}}_{\Lambda }$ and special divisors. The main result is Theorem 10.2. To proceed we first study the decomposition of ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ when
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ when ![]() $\mathrm {v}(L^\flat )=0$. Since
$\mathrm {v}(L^\flat )=0$. Since ![]() $n$ is odd, we can without loss of generality assume that
$n$ is odd, we can without loss of generality assume that ![]() $\chi (\mathbb {V})=\chi (C)=1$. In the rest of the paper, we identify
$\chi (\mathbb {V})=\chi (C)=1$. In the rest of the paper, we identify ![]() $\mathbb {V}$ with
$\mathbb {V}$ with ![]() $C$ by the isomorphism
$C$ by the isomorphism ![]() $b$ defined in (2.3).
$b$ defined in (2.3).
10.1 Decomposition of  ${}^{\mathbb {L}}\mathcal {Z}^{\mathrm {Kra}}(L^\flat )$
${}^{\mathbb {L}}\mathcal {Z}^{\mathrm {Kra}}(L^\flat )$
Let ![]() $L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ where
$L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ where ![]() ${\bf x}_1,{\bf x}_2\in \mathbb {V}$ are linearly independent and the Hermitian form restricted to
${\bf x}_1,{\bf x}_2\in \mathbb {V}$ are linearly independent and the Hermitian form restricted to ![]() $L$ is non-degenerate.
$L$ is non-degenerate.
Lemma 10.1 We have that ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )=[\mathcal {O}_{\mathcal {Z}^\mathrm {Kra}({\bf x}_1)}\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}^\mathrm {Kra}({\bf x}_2)}]\in K_0(\mathcal {N}^\mathrm {Kra})$ is, in fact, in
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )=[\mathcal {O}_{\mathcal {Z}^\mathrm {Kra}({\bf x}_1)}\otimes ^\mathbb {L} \mathcal {O}_{\mathcal {Z}^\mathrm {Kra}({\bf x}_2)}]\in K_0(\mathcal {N}^\mathrm {Kra})$ is, in fact, in ![]() $\mathrm {F}^{2} K_0(\mathcal {N}^\mathrm {Kra})$. Moreover, we have the decomposition in
$\mathrm {F}^{2} K_0(\mathcal {N}^\mathrm {Kra})$. Moreover, we have the decomposition in ![]() $\mathrm {Gr}^2 K_0^{\mathcal {Z}^\mathrm {Kra}(L^\flat )}(\mathcal {N}^\mathrm {Kra})$:
$\mathrm {Gr}^2 K_0^{\mathcal {Z}^\mathrm {Kra}(L^\flat )}(\mathcal {N}^\mathrm {Kra})$:
where ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )_h$ is described in Theorem 4.2 and
$\mathcal {Z}^\mathrm {Kra}(L^\flat )_h$ is described in Theorem 4.2 and ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L)_v\in \mathrm {Gr}^2 K_0^{\mathcal {Z}^\mathrm {Kra}(L^\flat )_v}(\mathcal {N}^\mathrm {Kra})$.
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L)_v\in \mathrm {Gr}^2 K_0^{\mathcal {Z}^\mathrm {Kra}(L^\flat )_v}(\mathcal {N}^\mathrm {Kra})$.
Proof. By Lemma 2.10, ![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is Noetherian and has a decomposition
$\mathcal {Z}^\mathrm {Kra}(L^\flat )$ is Noetherian and has a decomposition
Expressing ![]() $\mathcal {Z}({\bf x}_i)$ (
$\mathcal {Z}({\bf x}_i)$ (![]() $i=1,2$) as in (3.1) and applying Propositions 3.2, 3.3 and Lemma 3.4,
$i=1,2$) as in (3.1) and applying Propositions 3.2, 3.3 and Lemma 3.4, ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ equals
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )$ equals
![]() $\mathcal {Z}^\mathrm {Kra}(L^\flat )_h$ is contained in
$\mathcal {Z}^\mathrm {Kra}(L^\flat )_h$ is contained in ![]() $\tilde {\mathcal {Z}}({\bf x}_1)\cap \tilde {\mathcal {Z}}({\bf x}_2)$ and has dimension
$\tilde {\mathcal {Z}}({\bf x}_1)\cap \tilde {\mathcal {Z}}({\bf x}_2)$ and has dimension ![]() $1$ by Theorem 4.2;
$1$ by Theorem 4.2; ![]() $\tilde {\mathcal {Z}}({\bf x}_1)\cap \tilde {\mathcal {Z}}({\bf x}_2)_v$ also has dimension
$\tilde {\mathcal {Z}}({\bf x}_1)\cap \tilde {\mathcal {Z}}({\bf x}_2)_v$ also has dimension ![]() $1$ as it is supported on the reduced locus of
$1$ as it is supported on the reduced locus of ![]() $\mathcal {N}^\mathrm {Kra}$ by Lemma 2.11 and does not contain any exceptional divisor
$\mathcal {N}^\mathrm {Kra}$ by Lemma 2.11 and does not contain any exceptional divisor ![]() $\mathrm {Exc}_{\Lambda _0}$. Hence,
$\mathrm {Exc}_{\Lambda _0}$. Hence,
see, for example, [Reference ZhangZha21, Lemma B.2]. Hence, we know that ![]() ${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L^\flat )\in \mathrm {F}^{2} K_0(\mathcal {N}^\mathrm {Kra})$. The desired decomposition then follows from Theorem 4.2.
${}^\mathbb {L}\mathcal {Z}^\mathrm {Kra}(L^\flat )\in \mathrm {F}^{2} K_0(\mathcal {N}^\mathrm {Kra})$. The desired decomposition then follows from Theorem 4.2.
By Lemma 10.1 and (2.9) we know that ![]() ${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )_v\in K'_0(Y)$ where we can take
${}^\mathbb {L} \mathcal {Z}^\mathrm {Kra}(L^\flat )_v\in K'_0(Y)$ where we can take ![]() $Y$ to be the reduced locus of
$Y$ to be the reduced locus of ![]() $\mathcal {N}^\mathrm {Kra}$. By the Bruhat–Tits stratification of
$\mathcal {N}^\mathrm {Kra}$. By the Bruhat–Tits stratification of ![]() $\mathcal {N}^\mathrm {Kra}$ and the fact that
$\mathcal {N}^\mathrm {Kra}$ and the fact that ![]() $\mathrm {Gr}^1 K_0^{\mathrm {Exc}_{\Lambda _0}}(\mathcal {N}^\mathrm {Kra})\cong \mathrm {CH}^1(\mathrm {Exc}_{\Lambda _0})$ is generated by
$\mathrm {Gr}^1 K_0^{\mathrm {Exc}_{\Lambda _0}}(\mathcal {N}^\mathrm {Kra})\cong \mathrm {CH}^1(\mathrm {Exc}_{\Lambda _0})$ is generated by ![]() $H_{\Lambda _0}$, we have the following decomposition in
$H_{\Lambda _0}$, we have the following decomposition in ![]() $\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra})$:
$\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra})$:
We determine the multiplicities ![]() $m(\Lambda _2,L^\flat )$ and
$m(\Lambda _2,L^\flat )$ and ![]() $m(\Lambda _0,L^\flat )$ when
$m(\Lambda _0,L^\flat )$ when ![]() $\mathrm {v}(L^\flat )=0$ in this section and deal with the general case in § 11.
$\mathrm {v}(L^\flat )=0$ in this section and deal with the general case in § 11.
Now assume ![]() $L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ with Gram matrix
$L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ with Gram matrix ![]() $\mathrm {Diag}(u_1,u_2 (-\pi _0)^n)$ with
$\mathrm {Diag}(u_1,u_2 (-\pi _0)^n)$ with ![]() $u_1,u_2\in \mathcal {O}_{F_0}^\times$. Applying Proposition 3.2 to
$u_1,u_2\in \mathcal {O}_{F_0}^\times$. Applying Proposition 3.2 to ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x}_1)$, we find
$\mathcal {Z}^\mathrm {Kra}({\bf x}_1)$, we find
By Proposition 2.6, we know the intersection ![]() $\tilde {\mathcal {Z}}({\bf x}_1)\cap \mathcal {Z}^\mathrm {Kra}({\bf x}_2)$ is proper and is isomorphic to
$\tilde {\mathcal {Z}}({\bf x}_1)\cap \mathcal {Z}^\mathrm {Kra}({\bf x}_2)$ is proper and is isomorphic to ![]() $\mathcal {Z}^\mathrm {Kra}_{2,\chi (u_1)}({\bf x}_2)$. Combining this with Corollary 3.5 we obtain
$\mathcal {Z}^\mathrm {Kra}_{2,\chi (u_1)}({\bf x}_2)$. Combining this with Corollary 3.5 we obtain
where ![]() $i_*$ is the map
$i_*$ is the map ![]() $\mathrm {Gr}^1 K_0(\mathcal {N}^\mathrm {Kra}_{2,\chi (u_1)})\rightarrow \mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra}_{3,1})$ induced by the closed immersion
$\mathrm {Gr}^1 K_0(\mathcal {N}^\mathrm {Kra}_{2,\chi (u_1)})\rightarrow \mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra}_{3,1})$ induced by the closed immersion ![]() $i:\mathcal {N}^\mathrm {Kra}_{2,\chi (u_1)}\rightarrow \mathcal {N}^\mathrm {Kra}_{3,1}$. Equation (10.4) reduces the problem of decomposing
$i:\mathcal {N}^\mathrm {Kra}_{2,\chi (u_1)}\rightarrow \mathcal {N}^\mathrm {Kra}_{3,1}$. Equation (10.4) reduces the problem of decomposing ![]() ${}^{\mathbb {L}}\mathcal {Z}^{\mathrm {Kra}}(L^\flat )$ in this case to [Reference ShiShi22, Theorem 4.5] and [Reference He, Shi and YangHSY23, Theorem 4.1]. We do not make the effort to write the complete result down, but instead look at two basic examples.
${}^{\mathbb {L}}\mathcal {Z}^{\mathrm {Kra}}(L^\flat )$ in this case to [Reference ShiShi22, Theorem 4.5] and [Reference He, Shi and YangHSY23, Theorem 4.1]. We do not make the effort to write the complete result down, but instead look at two basic examples.
Let us begin by the case when ![]() $L^\flat$ is unimodular. By (10.4) and either [Reference ShiShi22, Theorem 4.5] or [Reference He, Shi and YangHSY23, Theorem 4.1], we have
$L^\flat$ is unimodular. By (10.4) and either [Reference ShiShi22, Theorem 4.5] or [Reference He, Shi and YangHSY23, Theorem 4.1], we have
in the notation of Theorem 4.2.
Next consider ![]() $L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ with Gram matrix
$L^\flat =\mathrm {Span}\{{\bf x}_1,{\bf x}_2\}$ with Gram matrix ![]() $\mathrm {Diag}(1,-u\pi _0)$ where
$\mathrm {Diag}(1,-u\pi _0)$ where ![]() $u\in \mathcal {O}_{F_0}^\times$. Then
$u\in \mathcal {O}_{F_0}^\times$. Then ![]() $\mathrm {Span}\{{\bf x}_1\}^{\perp }$ is split and
$\mathrm {Span}\{{\bf x}_1\}^{\perp }$ is split and ![]() $\tilde {\mathcal {Z}}({\bf x}_1)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$. By Proposition 9.7(3),
$\tilde {\mathcal {Z}}({\bf x}_1)\cong \mathcal {N}^\mathrm {Kra}_{2,1}$. By Proposition 9.7(3), ![]() $\mathcal {V}^2(L^\flat )$ consists of two adjacent lattices
$\mathcal {V}^2(L^\flat )$ consists of two adjacent lattices ![]() $\Lambda$ and
$\Lambda$ and ![]() $\Lambda '$. Moreover, by [Reference He, Shi and YangHSY23, Theorem 4.1] and (10.4), we have
$\Lambda '$. Moreover, by [Reference He, Shi and YangHSY23, Theorem 4.1] and (10.4), we have
10.2 The intersection number
Assume ![]() $\Lambda \in \mathcal {V}^2$. For
$\Lambda \in \mathcal {V}^2$. For ![]() ${\bf x}\in \mathbb {V}\backslash \{0\}$, define
${\bf x}\in \mathbb {V}\backslash \{0\}$, define
In this subsection we prove the following theorem.
Theorem 10.2 Let ![]() $\Lambda \in \mathcal {V}^2$ and
$\Lambda \in \mathcal {V}^2$ and ![]() ${\bf x}\in \mathbb {V}\backslash \{0\}$. Then
${\bf x}\in \mathbb {V}\backslash \{0\}$. Then
where ![]() $1_{\Lambda }$ is the characteristic function of
$1_{\Lambda }$ is the characteristic function of ![]() $\Lambda \subset \mathbb {V}$.
$\Lambda \subset \mathbb {V}$.
Corollary 10.3 Assume that ![]() $\Lambda _0\in \mathcal {L}_0$ and
$\Lambda _0\in \mathcal {L}_0$ and ![]() $\Lambda \in \mathcal {L}_2$ such that
$\Lambda \in \mathcal {L}_2$ such that ![]() $\Lambda _0\subset \Lambda$. Then for any
$\Lambda _0\subset \Lambda$. Then for any ![]() $y_0\in \Lambda _0\setminus \pi \Lambda _0$ such that
$y_0\in \Lambda _0\setminus \pi \Lambda _0$ such that ![]() $y_0^\bot$ is non-split, we have
$y_0^\bot$ is non-split, we have
Proof. By Proposition 3.2, we know
Now the corollary follows immediately from Theorem 10.2 and Lemma 9.12.
Proof of Theorem 10.2 We consider three different cases. First, if ![]() $x\notin \Lambda$ or
$x\notin \Lambda$ or ![]() $\mathrm {v}({\bf x})<0$, then by Lemma 9.2,
$\mathrm {v}({\bf x})<0$, then by Lemma 9.2, ![]() $\mathcal {Z}^\mathrm {Kra}({\bf x})\cap \tilde {\mathcal {N}}_\Lambda =\emptyset$, hence
$\mathcal {Z}^\mathrm {Kra}({\bf x})\cap \tilde {\mathcal {N}}_\Lambda =\emptyset$, hence ![]() $\mathrm {Int}_\Lambda ({\bf x})=0$. From now on we assume
$\mathrm {Int}_\Lambda ({\bf x})=0$. From now on we assume ![]() $x\in \Lambda$ and
$x\in \Lambda$ and ![]() $\mathrm {v}({\bf x})\geq 0$. Write
$\mathrm {v}({\bf x})\geq 0$. Write ![]() ${\bf x}= {\bf x}_0 \pi ^{n}$ with
${\bf x}= {\bf x}_0 \pi ^{n}$ with ![]() ${\bf x}_0 \in \Lambda \backslash \pi \Lambda$ and
${\bf x}_0 \in \Lambda \backslash \pi \Lambda$ and ![]() $n \ge 0$.
$n \ge 0$.
Case 1. First we assume ![]() ${\bf x}_0\in \Lambda \backslash \Lambda ^\sharp$. Choose a basis
${\bf x}_0\in \Lambda \backslash \Lambda ^\sharp$. Choose a basis ![]() $\{e'_1,e'_2,e'_3\}$ of
$\{e'_1,e'_2,e'_3\}$ of ![]() $\Lambda$ with Gram matrix
$\Lambda$ with Gram matrix ![]() $\mathcal {H}_{3,1}^1$ such that
$\mathcal {H}_{3,1}^1$ such that
Then one of ![]() $x$ and
$x$ and ![]() $y$ is in
$y$ is in ![]() $\mathcal {O}_{F}^\times$ as
$\mathcal {O}_{F}^\times$ as ![]() $\Lambda ^\sharp =\mathrm {Span}\{\pi e'_1, \pi e'_2, e_3\}$. Apparently the equation
$\Lambda ^\sharp =\mathrm {Span}\{\pi e'_1, \pi e'_2, e_3\}$. Apparently the equation
has a solution ![]() $(u,v)\in \mathcal {O}_{F_0}^2$ with
$(u,v)\in \mathcal {O}_{F_0}^2$ with ![]() $u\in \mathcal {O}_{F_0}^\times$. Now according to Lemma A.2, we can find a matrix
$u\in \mathcal {O}_{F_0}^\times$. Now according to Lemma A.2, we can find a matrix ![]() $g\in \mathrm {U}(\mathcal {H}_{3,1}^1)(\mathcal {O}_{F_0})$ such that
$g\in \mathrm {U}(\mathcal {H}_{3,1}^1)(\mathcal {O}_{F_0})$ such that
 \[ g\left(\begin{array}{c} x \\ y \\ z \end{array}\right)=\left(\begin{array}{c} \pi u \\ 1 \\ v \end{array}\right). \]
\[ g\left(\begin{array}{c} x \\ y \\ z \end{array}\right)=\left(\begin{array}{c} \pi u \\ 1 \\ v \end{array}\right). \]
Now replace the basis ![]() $\{e'_1,e'_2,e'_3\}$ by
$\{e'_1,e'_2,e'_3\}$ by ![]() $\{e_1,e_2,e_3\}=\{e'_1,e'_2,e'_3\}g^{-1}$, we have
$\{e_1,e_2,e_3\}=\{e'_1,e'_2,e'_3\}g^{-1}$, we have
where ![]() $u\in \mathcal {O}_{F_0}^\times$,
$u\in \mathcal {O}_{F_0}^\times$, ![]() $v\in \mathcal {O}_F$.
$v\in \mathcal {O}_F$.
Define
Then ![]() $\{f_1,f_2,f_3\}$ has also Gram matrix
$\{f_1,f_2,f_3\}$ has also Gram matrix ![]() $\mathcal {H}_{3,1}^1$ and
$\mathcal {H}_{3,1}^1$ and ![]() $\Lambda ':= \mathrm {Span}\{f_1,f_2,f_3\}$ is a type
$\Lambda ':= \mathrm {Span}\{f_1,f_2,f_3\}$ is a type ![]() $2$ lattice adjacent to
$2$ lattice adjacent to ![]() $\Lambda$ with
$\Lambda$ with ![]() $\Lambda _c=\Lambda \cap \Lambda '=\mathrm {Span}\{\pi e_1,e_2,e_3\}$ is a type
$\Lambda _c=\Lambda \cap \Lambda '=\mathrm {Span}\{\pi e_1,e_2,e_3\}$ is a type ![]() $0$ lattice. Now in terms of the basis
$0$ lattice. Now in terms of the basis ![]() $\{f_1,f_2,f_3\}$ we have
$\{f_1,f_2,f_3\}$ we have
Define ![]() $\theta \in \mathrm {U}(\mathbb {V})$ by taking the basis
$\theta \in \mathrm {U}(\mathbb {V})$ by taking the basis ![]() $\{e_1,e_2,e_3\}$ to
$\{e_1,e_2,e_3\}$ to ![]() $\{f_1,f_2,f_3\}$. Then
$\{f_1,f_2,f_3\}$. Then
In particular, ![]() $\theta (\mathcal {Z}^\mathrm {Kra}({\bf x}))=\mathcal {Z}^\mathrm {Kra}({\bf x})$ and
$\theta (\mathcal {Z}^\mathrm {Kra}({\bf x}))=\mathcal {Z}^\mathrm {Kra}({\bf x})$ and
Now let
![]() $L^\flat =\mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1\}$, and
$L^\flat =\mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1\}$, and ![]() $L=\mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1,{\bf x}\}$. Then by (10.6) and Theorem 4.2, we have
$L=\mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1,{\bf x}\}$. Then by (10.6) and Theorem 4.2, we have
where ![]() $\tilde {\mathcal {Z}}(M^\flat )$ is the quasi-canonical lifting cycle of the lattice
$\tilde {\mathcal {Z}}(M^\flat )$ is the quasi-canonical lifting cycle of the lattice
Combining with (10.9), we have
Let ![]() ${\bf x}'=\pi ^n(\pi u e_1+e_2)= {\bf x} - \pi ^n v e_3$. Then we have
${\bf x}'=\pi ^n(\pi u e_1+e_2)= {\bf x} - \pi ^n v e_3$. Then we have
 \begin{align*} \mathrm{Int}(L) &=\chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_0)\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x})\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1))\\ &=\chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_0)\cdot{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x}')\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1))\\ &=\chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})\\ &\quad +\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big), \end{align*}
\begin{align*} \mathrm{Int}(L) &=\chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_0)\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x})\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1))\\ &=\chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_0)\cdot{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x}')\cdot {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1))\\ &=\chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})\\ &\quad +\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big), \end{align*}
where we have used linear invariance [Reference HowardHow19, Corollary D] and Proposition 3.2. Note that the Gram matrix of ![]() $\{{\bf x}',\mathbf {y}_1\}$ is
$\{{\bf x}',\mathbf {y}_1\}$ is ![]() $\mathrm {Diag}(2u(-\pi _0)^n,-2u\pi _0)$. By Proposition 2.6 and [Reference He, Shi and YangHSY23, Theorem 1.1],
$\mathrm {Diag}(2u(-\pi _0)^n,-2u\pi _0)$. By Proposition 2.6 and [Reference He, Shi and YangHSY23, Theorem 1.1],
 \[ \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=\begin{cases} 1, & \text{if } n=0,\\ 1+n-2q, & \text{if } n\geq 1. \end{cases} \]
\[ \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=\begin{cases} 1, & \text{if } n=0,\\ 1+n-2q, & \text{if } n\geq 1. \end{cases} \]
By Corollary 3.6 and [Reference He, Shi and YangHSY23, Lemma 3.15], we know that
 \[ \sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=|\mathcal{V}^0(L)| =\begin{cases} 1, & \text{if } n=0,\\ 2q+1, & \text{if } n\geq 1.\end{cases} \]
\[ \sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=|\mathcal{V}^0(L)| =\begin{cases} 1, & \text{if } n=0,\\ 2q+1, & \text{if } n\geq 1.\end{cases} \]
Combining the above two equations we know that
On the other hand, by Corollary 3.8,
By [Reference GrossGro86, Proposition 3.3]
Hence, we obtain by (10.11)
Case 2. Now we assume ![]() ${\bf x}_0\in \Lambda ^\sharp \backslash \pi \Lambda$. As in the proof of the previous case, we can find a basis
${\bf x}_0\in \Lambda ^\sharp \backslash \pi \Lambda$. As in the proof of the previous case, we can find a basis ![]() $\{e_1,e_2,e_3\}$ of
$\{e_1,e_2,e_3\}$ of ![]() $\Lambda$ with Gram matrix
$\Lambda$ with Gram matrix ![]() $\mathcal {H}_{3,1}^1$ by Lemma A.4 such that
$\mathcal {H}_{3,1}^1$ by Lemma A.4 such that
where ![]() $u\in \mathcal {O}_{F_0}^\times$. Define
$u\in \mathcal {O}_{F_0}^\times$. Define
then ![]() ${\bf x}_0\in \Lambda '\backslash \Lambda '^\sharp$. Also define
${\bf x}_0\in \Lambda '\backslash \Lambda '^\sharp$. Also define
and ![]() $L^\flat := \mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1\}$. Then by Theorem 4.2 and (10.6) we have
$L^\flat := \mathrm {Span}\{\mathbf {y}_0,\mathbf {y}_1\}$. Then by Theorem 4.2 and (10.6) we have
where ![]() $\tilde {\mathcal {Z}}(M^\flat )$ is the quasi-canonical lifting cycle of the lattice
$\tilde {\mathcal {Z}}(M^\flat )$ is the quasi-canonical lifting cycle of the lattice
Let ![]() ${\bf x}':= \pi ^{n+1} e_1={\bf x} -\pi ^n u e_3$, then we have
${\bf x}':= \pi ^{n+1} e_1={\bf x} -\pi ^n u e_3$, then we have
 \begin{align*} \chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x})\cdot{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L^\flat)) &=\chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big)\\ &\quad +\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big). \end{align*}
\begin{align*} \chi(\mathcal{N}^\mathrm{Kra}, {}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x})\cdot{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L^\flat)) &=\chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big)\\ &\quad +\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big). \end{align*}
Note that the Gram matrix of ![]() $\{{\bf x}',\mathbf {y}_1\}$ is equivalent to
$\{{\bf x}',\mathbf {y}_1\}$ is equivalent to ![]() $\mathcal {H}_1$ when
$\mathcal {H}_1$ when ![]() $n=0$, and to
$n=0$, and to ![]() $\mathrm {Diag}(u_1\pi _0^n,u_2\pi _0)$ for some
$\mathrm {Diag}(u_1\pi _0^n,u_2\pi _0)$ for some ![]() $u_1,u_2\in \mathcal {O}_{F_0}^\times$ when
$u_1,u_2\in \mathcal {O}_{F_0}^\times$ when ![]() $n\geq 1$. Hence, by Proposition 2.6 and [Reference He, Shi and YangHSY23, Theorem 1.1], we know that
$n\geq 1$. Hence, by Proposition 2.6 and [Reference He, Shi and YangHSY23, Theorem 1.1], we know that
 \[ \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=\begin{cases} -(q-1), & \text{if } n=0,\\ 1+n-2q, & \text{if } n\geq 1. \end{cases} \]
\[ \chi(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\tilde{\mathcal{Z}}(\mathbf{y}_0)}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)})=\begin{cases} -(q-1), & \text{if } n=0,\\ 1+n-2q, & \text{if } n\geq 1. \end{cases} \]
By Corollary 3.6 and Lemmas 3.15 and 3.16 of [Reference He, Shi and YangHSY23], we know that
 \[ \sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big) =|\mathcal{V}^0(L)|=\begin{cases} q+1, & \text{if } n=0,\\ 2q+1, & \text{if } n\geq 1. \end{cases} \]
\[ \sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra}, \mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}({\bf x}')}\otimes^\mathbb{L}\mathcal{O}_{\mathcal{Z}^\mathrm{Kra}(\mathbf{y}_1)}\big) =|\mathcal{V}^0(L)|=\begin{cases} q+1, & \text{if } n=0,\\ 2q+1, & \text{if } n\geq 1. \end{cases} \]
Hence, we know that
On the other hand, by Corollary 3.8,
By [Reference GrossGro86, Proposition 3.3]
Since ![]() ${\bf x}\in \Lambda '\backslash \Lambda '^\sharp$, by the previous case we also have
${\bf x}\in \Lambda '\backslash \Lambda '^\sharp$, by the previous case we also have
Combining all of the above, we have by (10.13)
This finishes the proof of Theorem 10.2.
11. Proof of the modified Kudla–Rapoport conjecture: three-dimensional case
In this section, we prove Theorem 1.2. We need some preparation.
Proposition 11.1 Assume that ![]() $L \subset \mathbb {V}$ has a Gram matrix
$L \subset \mathbb {V}$ has a Gram matrix ![]() $T=\mathrm {Diag}(u_1, u_2 (-\pi _0)^{b}, u_3 (-\pi _0)^c)$ with
$T=\mathrm {Diag}(u_1, u_2 (-\pi _0)^{b}, u_3 (-\pi _0)^c)$ with ![]() $u_i \in \mathcal {O}_{F_0}^\times$ and
$u_i \in \mathcal {O}_{F_0}^\times$ and ![]() $0 \le b \le c$. Then
$0 \le b \le c$. Then
Moreover, for every decomposition ![]() $L =L^\flat \oplus \mathrm {Span}\{{\bf x}\}$, we have
$L =L^\flat \oplus \mathrm {Span}\{{\bf x}\}$, we have
Proof. Fix a basis ![]() $\{{\bf x}_1,{\bf x}_2,{\bf x}_3\}$ of
$\{{\bf x}_1,{\bf x}_2,{\bf x}_3\}$ of ![]() $L$ such that the Gram matrix of
$L$ such that the Gram matrix of ![]() $\{{\bf x}_1,{\bf x}_2,{\bf x}_3\}$ is
$\{{\bf x}_1,{\bf x}_2,{\bf x}_3\}$ is ![]() $T=\mathrm {Diag}(u_1, T_2)$ where
$T=\mathrm {Diag}(u_1, T_2)$ where ![]() $u_1\in \mathcal {O}_{F_0}^\times$ and
$u_1\in \mathcal {O}_{F_0}^\times$ and ![]() $T_2\in \mathrm {Herm}_2(\mathcal {O}_{F})$. Let
$T_2\in \mathrm {Herm}_2(\mathcal {O}_{F})$. Let ![]() $u_1^{-1}\cdot L$ be a lattice represented by
$u_1^{-1}\cdot L$ be a lattice represented by ![]() $u_1^{-1}\cdot T$. Since
$u_1^{-1}\cdot T$. Since ![]() $\mathrm {Int}(u_1^{-1}\cdot L)=\mathrm {Int}(L)$ and
$\mathrm {Int}(u_1^{-1}\cdot L)=\mathrm {Int}(L)$ and ![]() $\partial \mathrm {Den}(u_1^{-1}\cdot L)=\partial \mathrm {Den}(L)$, we may assume
$\partial \mathrm {Den}(u_1^{-1}\cdot L)=\partial \mathrm {Den}(L)$, we may assume ![]() $u_1=1$. Let
$u_1=1$. Let ![]() $L^{\flat }=\mathrm {Span}\{{\bf x}_2,{\bf x}_3\}$. According to Propositions 2.6 and 3.2 and Corollary 3.6, we have
$L^{\flat }=\mathrm {Span}\{{\bf x}_2,{\bf x}_3\}$. According to Propositions 2.6 and 3.2 and Corollary 3.6, we have
 \begin{align} \mathrm{Int}(L)-\mathrm{Int}(L^\flat) & =\chi\big(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x}_1)\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)-\chi\big(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\tilde{\mathcal{Z}}({\bf x}_1)\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)\nonumber\\ &=\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra},[\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}]\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)\nonumber\\ &=|\{\mathcal{V}^0(L)\}|. \end{align}
\begin{align} \mathrm{Int}(L)-\mathrm{Int}(L^\flat) & =\chi\big(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}({\bf x}_1)\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)-\chi\big(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\tilde{\mathcal{Z}}({\bf x}_1)\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)\nonumber\\ &=\sum_{\Lambda_0\in \mathcal{V}^0(L)} \chi\big(\mathcal{N}^\mathrm{Kra},[\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}]\cdot {}^{\mathbb{L}}\mathcal{Z}^{\mathrm{Kra}}(L^\flat)\big)\nonumber\\ &=|\{\mathcal{V}^0(L)\}|. \end{align}
Now the result we want follows by comparing (11.1) with (8.5), and the identity ![]() $\mathrm {Int}(L^\flat )=\partial \mathrm {Den}(L^\flat )$ proved in [Reference ShiShi22, Theorem 1.3] and [Reference He, Shi and YangHSY23, Theorem 1.3]. Part (2) follows from part (1) and Theorem 5.6(2).
$\mathrm {Int}(L^\flat )=\partial \mathrm {Den}(L^\flat )$ proved in [Reference ShiShi22, Theorem 1.3] and [Reference He, Shi and YangHSY23, Theorem 1.3]. Part (2) follows from part (1) and Theorem 5.6(2).
Proof of Theorem 1.4 Under the assumption ![]() $\mathrm {v}(L^\flat )>0$, we can decompose
$\mathrm {v}(L^\flat )>0$, we can decompose ![]() $\mathcal {D}(L^\flat )$ in
$\mathcal {D}(L^\flat )$ in ![]() $\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra})$ as
$\mathrm {Gr}^2 K_0(\mathcal {N}^\mathrm {Kra})$ as
by (10.3) and Proposition 4.6.
Claim 1 We claim that ![]() $m(\mathcal {D}(L^\flat ),\Lambda _0)=0$ unless
$m(\mathcal {D}(L^\flat ),\Lambda _0)=0$ unless ![]() $L^\flat \subset \Lambda _0$. In such a case,
$L^\flat \subset \Lambda _0$. In such a case,
 \begin{equation} m(\mathcal{D}(L^\flat),\Lambda_0)=\begin{cases} q+1, & \text{if }\Lambda_0\in \mathcal{V}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ 1, & \text{if }\Lambda_0\in \mathcal{B}(L^\flat). \end{cases} \end{equation}
\begin{equation} m(\mathcal{D}(L^\flat),\Lambda_0)=\begin{cases} q+1, & \text{if }\Lambda_0\in \mathcal{V}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ 1, & \text{if }\Lambda_0\in \mathcal{B}(L^\flat). \end{cases} \end{equation}
Indeed, since ![]() $\Lambda _0$ is of type
$\Lambda _0$ is of type ![]() $0$, we may choose a
$0$, we may choose a ![]() $y_0\in \mathbb {V}\setminus L^\flat _F$ such that
$y_0\in \mathbb {V}\setminus L^\flat _F$ such that ![]() $\mathrm {Span}\{y_0\}^\bot$ is non-split and
$\mathrm {Span}\{y_0\}^\bot$ is non-split and ![]() $y_0 \in \Lambda _0\setminus \pi \Lambda _0$. In this case, Proposition 3.2 and Corollaries 3.7 and 3.8 imply that
$y_0 \in \Lambda _0\setminus \pi \Lambda _0$. In this case, Proposition 3.2 and Corollaries 3.7 and 3.8 imply that
Thus, by (11.2) and Corollaries 10.3 and 2.7, we have
Let ![]() $(2a,2b)$ (
$(2a,2b)$ (![]() $b>a$) be the fundamental invariant of the projection of
$b>a$) be the fundamental invariant of the projection of ![]() $L^\flat$ onto
$L^\flat$ onto ![]() $\mathrm {Span}\{y_0\}^\bot$. Let
$\mathrm {Span}\{y_0\}^\bot$. Let ![]() $\varphi$ be the natural quotient map
$\varphi$ be the natural quotient map ![]() $\Lambda _0\rightarrow \Lambda _0/\pi \Lambda _0$ and define
$\Lambda _0\rightarrow \Lambda _0/\pi \Lambda _0$ and define
Equation (9.1) implies that ![]() $m=0$ if and only if
$m=0$ if and only if ![]() $\Lambda _0\in \mathcal {L}(L^\flat )\setminus \mathcal {B}(L^\flat )$. First assume
$\Lambda _0\in \mathcal {L}(L^\flat )\setminus \mathcal {B}(L^\flat )$. First assume ![]() $m=0$, in other words,
$m=0$, in other words, ![]() $L^\flat \subset \pi \Lambda _0$ so
$L^\flat \subset \pi \Lambda _0$ so ![]() $b\geq a \geq 1$. By the definition of
$b\geq a \geq 1$. By the definition of ![]() $\mathcal {D}(L^\flat )$ and [Reference ShiShi22, Theorem 1.2], we have
$\mathcal {D}(L^\flat )$ and [Reference ShiShi22, Theorem 1.2], we have
as claimed where
 \begin{equation} \mu(a,b)=\chi(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L^\flat) \cdot [\mathcal{O}_{\tilde{\mathcal{Z}}(y_0)}])=\begin{cases} 2\displaystyle\sum_{s=0}^{a}q^s(a+b+1-2s)-a-b-2, & \text{if } a\geq 0\\ 0, & \text{if } a<0. \end{cases}\end{equation}
\begin{equation} \mu(a,b)=\chi(\mathcal{N}^\mathrm{Kra},{}^\mathbb{L}\mathcal{Z}^\mathrm{Kra}(L^\flat) \cdot [\mathcal{O}_{\tilde{\mathcal{Z}}(y_0)}])=\begin{cases} 2\displaystyle\sum_{s=0}^{a}q^s(a+b+1-2s)-a-b-2, & \text{if } a\geq 0\\ 0, & \text{if } a<0. \end{cases}\end{equation} Now assume ![]() $m=1$, then
$m=1$, then ![]() $\varphi (L^\flat )$ is a line
$\varphi (L^\flat )$ is a line ![]() $\ell$ and
$\ell$ and ![]() $b\geq 1$. By the assumption that
$b\geq 1$. By the assumption that ![]() $y_0\notin L^\flat _F$, we know
$y_0\notin L^\flat _F$, we know ![]() $\ell$ is not in
$\ell$ is not in ![]() $\mathrm {Span}\{\varphi (y_0)\}$, hence the projection of
$\mathrm {Span}\{\varphi (y_0)\}$, hence the projection of ![]() $\ell$ onto
$\ell$ onto ![]() $\varphi (y_0)^\bot$ is non-zero. Since
$\varphi (y_0)^\bot$ is non-zero. Since ![]() $\varphi (y_0)^\bot$ is non-split, we must have
$\varphi (y_0)^\bot$ is non-split, we must have ![]() $a=0$. Hence, by the definition of
$a=0$. Hence, by the definition of ![]() $\mathcal {D}(L^\flat )$ and (11.4), we have
$\mathcal {D}(L^\flat )$ and (11.4), we have
as claimed. Finally, ![]() $m=2$ is impossible since
$m=2$ is impossible since ![]() $v(L^\flat ) >0$. This finishes the proof of Claim 1.
$v(L^\flat ) >0$. This finishes the proof of Claim 1.
Claim 2 We claim that ![]() $m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ for any
$m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ for any ![]() $\Lambda _2 \in \mathcal {V}^2(L^\flat )$.
$\Lambda _2 \in \mathcal {V}^2(L^\flat )$.
Indeed, according to Lemma 3.9, we have ![]() $\chi (\mathcal {N}^\mathrm {Kra},\mathcal {D}(L^\flat ) \cdot [\mathcal {O}_{\mathrm {Exc}_{\Lambda _0}}])=0$. On the other hand, Corollary 3.7 and Lemma 9.12 imply that
$\chi (\mathcal {N}^\mathrm {Kra},\mathcal {D}(L^\flat ) \cdot [\mathcal {O}_{\mathrm {Exc}_{\Lambda _0}}])=0$. On the other hand, Corollary 3.7 and Lemma 9.12 imply that
Combining the above with Claim 1, we have
 \begin{equation} 0=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat) \cdot [\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}])=\begin{cases} \displaystyle\sum_{\Lambda_0\subset \Lambda_2 }m(\mathcal{D}(L^\flat),\Lambda_2)-2(q+1), & \text{if }\Lambda_0 \in \mathcal{L}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ \displaystyle\sum_{\Lambda_0\subset \Lambda_2 }m(\mathcal{D}(L^\flat),\Lambda_2)-2, & \text{if }\Lambda_0 \in \mathcal{B}(L^\flat).\end{cases} \end{equation}
\begin{equation} 0=\chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat) \cdot [\mathcal{O}_{\mathrm{Exc}_{\Lambda_0}}])=\begin{cases} \displaystyle\sum_{\Lambda_0\subset \Lambda_2 }m(\mathcal{D}(L^\flat),\Lambda_2)-2(q+1), & \text{if }\Lambda_0 \in \mathcal{L}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ \displaystyle\sum_{\Lambda_0\subset \Lambda_2 }m(\mathcal{D}(L^\flat),\Lambda_2)-2, & \text{if }\Lambda_0 \in \mathcal{B}(L^\flat).\end{cases} \end{equation}
Recall ![]() $\mathcal {S}(L^\flat )$ in Definition 9.8. First assume
$\mathcal {S}(L^\flat )$ in Definition 9.8. First assume ![]() $\Lambda _2\in \mathcal {L}(L^\flat )\setminus \mathcal {S}(L^\flat )$. If
$\Lambda _2\in \mathcal {L}(L^\flat )\setminus \mathcal {S}(L^\flat )$. If ![]() $d(\Lambda _2,\mathcal {B}(L^\flat ))$ is equal to
$d(\Lambda _2,\mathcal {B}(L^\flat ))$ is equal to ![]() $\tfrac {1}{2}$, choose
$\tfrac {1}{2}$, choose ![]() $\Lambda _0\in \mathcal {B}(L^\flat )$ such that
$\Lambda _0\in \mathcal {B}(L^\flat )$ such that ![]() $\Lambda _0\subset \Lambda _2$, then
$\Lambda _0\subset \Lambda _2$, then ![]() $\Lambda _2$ is the unique lattice in
$\Lambda _2$ is the unique lattice in ![]() $\mathcal {V}^2(L^\flat )$ that contains
$\mathcal {V}^2(L^\flat )$ that contains ![]() $\Lambda _0$, hence (11.6) implies that
$\Lambda _0$, hence (11.6) implies that ![]() $m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ in this case. Now Corollary 9.10 allows us to show
$m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ in this case. Now Corollary 9.10 allows us to show ![]() $m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ by induction on the distance
$m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ by induction on the distance ![]() $d(\Lambda _2,\mathcal {B}(L^\flat ))$ for any
$d(\Lambda _2,\mathcal {B}(L^\flat ))$ for any ![]() $\Lambda _2\in \mathcal {L}(L^\flat )\setminus \mathcal {S}(L^\flat )$.
$\Lambda _2\in \mathcal {L}(L^\flat )\setminus \mathcal {S}(L^\flat )$.
Similarly for ![]() $\Lambda _2\in \mathcal {S}(L^\flat )$, we can show
$\Lambda _2\in \mathcal {S}(L^\flat )$, we can show ![]() $m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ by induction on its distance to
$m(\mathcal {D}(L^\flat ),\Lambda _2)=2$ by induction on its distance to ![]() $\mathcal {S}(L^\flat )\cap \mathcal {B}(L^\flat )$. This finishes the proof of Claim 2.
$\mathcal {S}(L^\flat )\cap \mathcal {B}(L^\flat )$. This finishes the proof of Claim 2.
Note that for ![]() $\Lambda _0 \in \mathcal {V}(L^\flat )$
$\Lambda _0 \in \mathcal {V}(L^\flat )$
 \[ \sum_{\Lambda_2 \in \mathcal{V}^2(L^\flat)} \sum_{\Lambda_0 \subset \Lambda_2} 1 = \begin{cases} q+1, & \text{if }\Lambda_0 \in \mathcal{V}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ 1, & \text{if } \Lambda_0 \in \mathcal{B}(L^\flat). \end{cases} \]
\[ \sum_{\Lambda_2 \in \mathcal{V}^2(L^\flat)} \sum_{\Lambda_0 \subset \Lambda_2} 1 = \begin{cases} q+1, & \text{if }\Lambda_0 \in \mathcal{V}(L^\flat)\setminus \mathcal{B}(L^\flat),\\ 1, & \text{if } \Lambda_0 \in \mathcal{B}(L^\flat). \end{cases} \]
This finishes the proof of Theorem 1.4.
In the following discussion we freely use Theorem 10.2 and Corollary 3.8 without explicitly referring to them.
Proposition 11.2 Assume ![]() $L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$ with Gram matrix
$L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$ with Gram matrix
where ![]() $a$ is a positive odd integer, and
$a$ is a positive odd integer, and ![]() $c\ge 0$. Then
$c\ge 0$. Then
 \begin{equation} \mathrm{Int}(L)^{(2)}=\partial \mathrm{Den} (L)^{(2)}= \begin{cases} 1-q^{a}, & \text{if }a\le 2c,\\ 1-q^{2c+1}, & \text{if }a> 2c. \end{cases} \end{equation}
\begin{equation} \mathrm{Int}(L)^{(2)}=\partial \mathrm{Den} (L)^{(2)}= \begin{cases} 1-q^{a}, & \text{if }a\le 2c,\\ 1-q^{2c+1}, & \text{if }a> 2c. \end{cases} \end{equation}Proof. By Proposition 8.5, it suffices to prove the identity for ![]() $\mathrm {Int}(L)^{(2)}$.
$\mathrm {Int}(L)^{(2)}$.
Now we compute ![]() $\mathrm {Int}(L)^{(2)}$. We may take
$\mathrm {Int}(L)^{(2)}$. We may take ![]() $L^\flat =\mathrm {Span}\{\pi ^{({a+1})/2} e_1,\pi ^{({a+1})/2} e_2\}$, where the Gram matrix of
$L^\flat =\mathrm {Span}\{\pi ^{({a+1})/2} e_1,\pi ^{({a+1})/2} e_2\}$, where the Gram matrix of ![]() $\{e_1,e_2\}$ is
$\{e_1,e_2\}$ is ![]() $\mathcal {H}$. Let
$\mathcal {H}$. Let ![]() $e_3=\pi ^{-c} {\bf x}$. Then
$e_3=\pi ^{-c} {\bf x}$. Then ![]() $\mathcal {L}(L^\flat )$ is centered at
$\mathcal {L}(L^\flat )$ is centered at ![]() $\mathrm {Span}\{e_1,e_2,e_3\}$ of radius
$\mathrm {Span}\{e_1,e_2,e_3\}$ of radius ![]() ${a}/{2}$ by Proposition 9.7.
${a}/{2}$ by Proposition 9.7.
Assume ![]() $a\le 2c$ first. In this case,
$a\le 2c$ first. In this case, ![]() $\mathcal {L}(L^\flat )\subset \mathcal {L}({\bf x})$. As a result, we have
$\mathcal {L}(L^\flat )\subset \mathcal {L}({\bf x})$. As a result, we have ![]() $\mathrm {Int}_{\Lambda _2}({\bf x})=1$ and
$\mathrm {Int}_{\Lambda _2}({\bf x})=1$ and ![]() $\mathrm {Int}_{\Lambda _0}({\bf x})=-1$ for any
$\mathrm {Int}_{\Lambda _0}({\bf x})=-1$ for any ![]() $\Lambda _2\in \mathcal {V}^2(L^\flat )$ and
$\Lambda _2\in \mathcal {V}^2(L^\flat )$ and ![]() $\Lambda _0\in \mathcal {V}^0(L^\flat )$. Hence, by Theorem 1.4, we have
$\Lambda _0\in \mathcal {V}^0(L^\flat )$. Hence, by Theorem 1.4, we have
 \begin{align} \mathrm{Int}(L)^{(2)} &=\sum_{\Lambda_2\in \mathcal{L}(L^{\flat})}\chi\biggl(\mathcal{N}^\mathrm{Kra}, \biggl(2\big[\mathcal{O}_{\tilde{\mathcal{N}}_{\Lambda_2}}\big]+\sum_{\Lambda_0\subset \Lambda_2}H_{\Lambda_0}\biggr)\cdot \mathcal{Z}^{\mathrm{Kra}}({\bf x})\biggr)\nonumber\\ &=(1-q)|\{\Lambda_2\mid \Lambda_2\in \mathcal{L}(L^\flat)\}| \nonumber\\ &=(1-q)(1+(1+q)q+(1+q)q^3+\cdots+(1+q)q^{a-2})\nonumber\\ &=1-q^a, \end{align}
\begin{align} \mathrm{Int}(L)^{(2)} &=\sum_{\Lambda_2\in \mathcal{L}(L^{\flat})}\chi\biggl(\mathcal{N}^\mathrm{Kra}, \biggl(2\big[\mathcal{O}_{\tilde{\mathcal{N}}_{\Lambda_2}}\big]+\sum_{\Lambda_0\subset \Lambda_2}H_{\Lambda_0}\biggr)\cdot \mathcal{Z}^{\mathrm{Kra}}({\bf x})\biggr)\nonumber\\ &=(1-q)|\{\Lambda_2\mid \Lambda_2\in \mathcal{L}(L^\flat)\}| \nonumber\\ &=(1-q)(1+(1+q)q+(1+q)q^3+\cdots+(1+q)q^{a-2})\nonumber\\ &=1-q^a, \end{align}as claimed.
Now we assume ![]() $a>2c$. We consider the case
$a>2c$. We consider the case ![]() $c=0$ first. Recall that
$c=0$ first. Recall that ![]() $\tilde {\mathcal {Z}}(e_3)\approx \mathcal {N}^{\mathrm {Kra}}_{2,1}$, hence
$\tilde {\mathcal {Z}}(e_3)\approx \mathcal {N}^{\mathrm {Kra}}_{2,1}$, hence ![]() $\mathcal {L}(L^\flat )\cap \mathcal {L}(e_3)$ is a ball of radius
$\mathcal {L}(L^\flat )\cap \mathcal {L}(e_3)$ is a ball of radius ![]() ${a}/{2}$ in the Bruhat–Tits tree
${a}/{2}$ in the Bruhat–Tits tree ![]() $\mathcal {L}_{2,1}$ of
$\mathcal {L}_{2,1}$ of ![]() $\mathcal {N}^{\mathrm {Pap}}_{2,1}$ centered at the vertex lattice corresponding to
$\mathcal {N}^{\mathrm {Pap}}_{2,1}$ centered at the vertex lattice corresponding to ![]() $\pi ^{-({a+1})/{2}}\,{\cdot}\, L^\flat$, within which a vertex lattice
$\pi ^{-({a+1})/{2}}\,{\cdot}\, L^\flat$, within which a vertex lattice ![]() $\Lambda _0$ of type
$\Lambda _0$ of type ![]() $0$ is contained in two vertex lattices of type
$0$ is contained in two vertex lattices of type ![]() $2$, and a vertex lattice
$2$, and a vertex lattice ![]() $\Lambda _2$ of type
$\Lambda _2$ of type ![]() $2$ contains
$2$ contains ![]() $q+1$ vertex lattice of type
$q+1$ vertex lattice of type ![]() $0$. Hence,
$0$. Hence,
and
Moreover, note that if ![]() $e_3\in \Lambda _0$, then
$e_3\in \Lambda _0$, then ![]() $\mathrm {Int}_{\Lambda _2}(e_3)=1$ for any
$\mathrm {Int}_{\Lambda _2}(e_3)=1$ for any ![]() $\Lambda _2$ such that
$\Lambda _2$ such that ![]() $\Lambda _0\subset \Lambda _2$. As a result,
$\Lambda _0\subset \Lambda _2$. As a result,
 \begin{align*}
\chi\big(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot
\mathcal{Z}^{\mathrm{Kra}}(e_3)\big) &=2(1+
q\cdot|\big\{\Lambda_0\mid \Lambda_0\in
\big(\mathcal{L}(L^\flat)\setminus
\mathcal{B}(L^\flat)\big)\cap \mathcal{L}(e_3)\big\}|)\\
&\quad -(q+1) |\{\Lambda_0\mid \Lambda_0\in
(\mathcal{L}(L^\flat)\setminus \mathcal{B}(L^\flat))\cap
\mathcal{L}(e_3)\}|\\ &\quad-|\big\{\Lambda_0\mid
\Lambda_0\in \mathcal{B}(L^\flat)\cap
\mathcal{L}(e_3)\big\}|\\
&=2+(q-1)(1+q+(1+q)q+\cdots+(1+q)q^{({a-3})/{2}})\\
&\quad-(1+q)q^{({a-1})/{2}}=1-q, \end{align*}
\begin{align*}
\chi\big(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot
\mathcal{Z}^{\mathrm{Kra}}(e_3)\big) &=2(1+
q\cdot|\big\{\Lambda_0\mid \Lambda_0\in
\big(\mathcal{L}(L^\flat)\setminus
\mathcal{B}(L^\flat)\big)\cap \mathcal{L}(e_3)\big\}|)\\
&\quad -(q+1) |\{\Lambda_0\mid \Lambda_0\in
(\mathcal{L}(L^\flat)\setminus \mathcal{B}(L^\flat))\cap
\mathcal{L}(e_3)\}|\\ &\quad-|\big\{\Lambda_0\mid
\Lambda_0\in \mathcal{B}(L^\flat)\cap
\mathcal{L}(e_3)\big\}|\\
&=2+(q-1)(1+q+(1+q)q+\cdots+(1+q)q^{({a-3})/{2}})\\
&\quad-(1+q)q^{({a-1})/{2}}=1-q, \end{align*}
which is compatible with (11.7).
Next we show
According to Proposition 9.6, ![]() $\mathcal {V}(\pi e_3)=\{\Lambda \mid d(\Lambda,\mathcal {L}(e_3))\le 1\}$. Hence, around each
$\mathcal {V}(\pi e_3)=\{\Lambda \mid d(\Lambda,\mathcal {L}(e_3))\le 1\}$. Hence, around each ![]() $\Lambda _0\in (\mathcal {L}(L^\flat )\setminus \mathcal {B}(L^\flat ))\cap \mathcal {L}(e_3)$, there will be
$\Lambda _0\in (\mathcal {L}(L^\flat )\setminus \mathcal {B}(L^\flat ))\cap \mathcal {L}(e_3)$, there will be ![]() $q(q-1)$ many new vertex lattices of type
$q(q-1)$ many new vertex lattices of type ![]() $0$ in
$0$ in ![]() $\mathcal {L}(L^\flat )\cap \mathcal {L}(\pi e_3)\setminus \mathcal {L}(L^\flat )\cap \mathcal {L}(e_3)$. Hence,
$\mathcal {L}(L^\flat )\cap \mathcal {L}(\pi e_3)\setminus \mathcal {L}(L^\flat )\cap \mathcal {L}(e_3)$. Hence,
 \begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot (\mathcal{Z}^{\mathrm{Kra}}(\pi e_3)-\mathcal{Z}^{\mathrm{Kra}}(e_3)))\\ &\quad =2q\cdot q(q-1)(1+q+(1+q)q+(1+q)q^2+\cdots+(1+q)q^{({a-1})/{2}-2})\\ &\qquad -q(q-1)(q+1)(1+q+(1+q)q+(1+q)q^2+\cdots+(1+q)q^{({a-1})/{2}-2})\\ &\qquad -q(q-1) (1+q)q^{({a-1})/{2}-1}\\ &\quad=q-q^{3}. \end{align*}
\begin{align*} &\chi(\mathcal{N}^\mathrm{Kra},\mathcal{D}(L^\flat)\cdot (\mathcal{Z}^{\mathrm{Kra}}(\pi e_3)-\mathcal{Z}^{\mathrm{Kra}}(e_3)))\\ &\quad =2q\cdot q(q-1)(1+q+(1+q)q+(1+q)q^2+\cdots+(1+q)q^{({a-1})/{2}-2})\\ &\qquad -q(q-1)(q+1)(1+q+(1+q)q+(1+q)q^2+\cdots+(1+q)q^{({a-1})/{2}-2})\\ &\qquad -q(q-1) (1+q)q^{({a-1})/{2}-1}\\ &\quad=q-q^{3}. \end{align*}
Continuing in this way, we can show
for ![]() $2i< a$. Thus,
$2i< a$. Thus,
as claimed.
Proposition 11.3 Assume ![]() $L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$ with Gram matrix
$L=L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$ with Gram matrix
where ![]() $0< a\le b \le c$, then
$0< a\le b \le c$, then
Proof. By Proposition 8.4, it suffices to show
Note that since ![]() $a\le b\le c$, we have
$a\le b\le c$, we have ![]() $\mathcal {L}(L^\flat )\subset \mathcal {L}({\bf x})$ by Propositions 9.6 and 9.7.
$\mathcal {L}(L^\flat )\subset \mathcal {L}({\bf x})$ by Propositions 9.6 and 9.7.
First, we assume ![]() $\chi (-u_2u_3)=-1$, then (11.9) specializes to
$\chi (-u_2u_3)=-1$, then (11.9) specializes to
On the other hand, ![]() $\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type
$\mathcal {L}(L^\flat )$ is a ball centered at a vertex lattice of type ![]() $0$ with radius
$0$ with radius ![]() $a$ in this case. One can show
$a$ in this case. One can show ![]() $\mathrm {Int}(L)^{(2)}=1-q^{2a}$ exactly as in (11.8).
$\mathrm {Int}(L)^{(2)}=1-q^{2a}$ exactly as in (11.8).
Now we assume ![]() $\chi (-u_2u_3)=1$. In this case, (11.9) specializes to
$\chi (-u_2u_3)=1$. In this case, (11.9) specializes to
Let ![]() $r=b-a$, and
$r=b-a$, and ![]() $L^\flat =\mathrm {Span}\{x_1,x_2\}$. Then
$L^\flat =\mathrm {Span}\{x_1,x_2\}$. Then ![]() $\mathcal {L}(\pi ^{-a}L^\flat )$ is a ball centered at a vertex lattice of type
$\mathcal {L}(\pi ^{-a}L^\flat )$ is a ball centered at a vertex lattice of type ![]() $0$ with radius
$0$ with radius ![]() $r$ in the Bruhat–Tits tree
$r$ in the Bruhat–Tits tree ![]() $\mathcal {L}_{2,1}$. Hence,
$\mathcal {L}_{2,1}$. Hence,
When ![]() $a=1$,
$a=1$, ![]() $\mathcal {V}^0(\pi ^{-1}L^\flat )=\mathcal {V}^0(L^\flat )\setminus \mathcal {B}(L^\flat )$. Then combining with Theorem 1.4, it is not hard to see
$\mathcal {V}^0(\pi ^{-1}L^\flat )=\mathcal {V}^0(L^\flat )\setminus \mathcal {B}(L^\flat )$. Then combining with Theorem 1.4, it is not hard to see
 \begin{align*} \mathrm{Int}(L)^{(2)} &=2(q+1+q\cdot 2(q+q^2+\cdots+q^r)) -(q+1)|\mathcal{V}^0(L^\flat)\setminus \mathcal{B}(L^\flat)|-|\mathcal{B}(L^\flat)|\\ &=1+q^2-2q^{b+1}, \end{align*}
\begin{align*} \mathrm{Int}(L)^{(2)} &=2(q+1+q\cdot 2(q+q^2+\cdots+q^r)) -(q+1)|\mathcal{V}^0(L^\flat)\setminus \mathcal{B}(L^\flat)|-|\mathcal{B}(L^\flat)|\\ &=1+q^2-2q^{b+1}, \end{align*}
where we use the fact
and
Now assume ![]() $a> 1$. Let
$a> 1$. Let ![]() $T$ be the Hermitian matrix associated with
$T$ be the Hermitian matrix associated with ![]() $L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$, then
$L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\}$, then
 \begin{align*} &\partial \mathrm{Den}
(\pi L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \partial
\mathrm{Den} (L^\flat{\unicode{x29BA}} \mathrm{Span}\{{\bf
x}\})^{(2)}\\ &\quad= 1+q^{2a+2}-2q^{r+2a+2}-(
1+q^{2a}-2q^{r+2a})\\ &\quad=q^{2a}(q^2-1)(1-q^{2r})\\
&\quad=q^2\big(\partial \mathrm{Den}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \partial
\mathrm{Den} (\pi^{-1}L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf
x}\})^{(2)}\big), \end{align*}
\begin{align*} &\partial \mathrm{Den}
(\pi L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \partial
\mathrm{Den} (L^\flat{\unicode{x29BA}} \mathrm{Span}\{{\bf
x}\})^{(2)}\\ &\quad= 1+q^{2a+2}-2q^{r+2a+2}-(
1+q^{2a}-2q^{r+2a})\\ &\quad=q^{2a}(q^2-1)(1-q^{2r})\\
&\quad=q^2\big(\partial \mathrm{Den}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \partial
\mathrm{Den} (\pi^{-1}L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf
x}\})^{(2)}\big), \end{align*}
and
 \begin{align*} &\mathrm{Int} (\pi
L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \mathrm{Int}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}\\
&\quad=2q|\mathcal{B}(L^\flat)|-q|\mathcal{B}(L^\flat)|-|\mathcal{B}(\pi
L^\flat)|\\ &\quad=(2q-q-q^2)|\mathcal{B}(L^\flat)|\\
&\quad=q^2\bigl(\mathrm{Int}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \mathrm{Int}
(\pi^{-1} L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf
x}\})^{(2)}\bigr), \end{align*}
\begin{align*} &\mathrm{Int} (\pi
L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \mathrm{Int}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}\\
&\quad=2q|\mathcal{B}(L^\flat)|-q|\mathcal{B}(L^\flat)|-|\mathcal{B}(\pi
L^\flat)|\\ &\quad=(2q-q-q^2)|\mathcal{B}(L^\flat)|\\
&\quad=q^2\bigl(\mathrm{Int}
(L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf x}\})^{(2)}- \mathrm{Int}
(\pi^{-1} L^\flat{\unicode{x29BA}}\mathrm{Span}\{{\bf
x}\})^{(2)}\bigr), \end{align*}
where we use the fact ![]() $|\mathcal {B}(\pi L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\})|=q^2|\mathcal {B}(L^\flat )|$. Since
$|\mathcal {B}(\pi L^\flat {\unicode{x29BA}} \mathrm {Span}\{{\bf x}\})|=q^2|\mathcal {B}(L^\flat )|$. Since ![]() $r$ is arbitrary, an induction on
$r$ is arbitrary, an induction on ![]() $a$ gives the result we want.
$a$ gives the result we want.
Proof of Theorem 1.2 The case ![]() $\mathrm {v}(L)< 0$ follows from Proposition 8.1 and the fact that
$\mathrm {v}(L)< 0$ follows from Proposition 8.1 and the fact that ![]() $\mathrm {Int}(L)=0$ under this condition. Assume
$\mathrm {Int}(L)=0$ under this condition. Assume ![]() $v(L) \ge 0$. There are three cases.
$v(L) \ge 0$. There are three cases.
Case 1. When ![]() $L$ has a Gram matrix
$L$ has a Gram matrix ![]() $\mathrm {Diag}(u_1, u_2(-\pi _0)^b, u_3 (-\pi _0)^c)$ as in Proposition 11.1, it is proved by Proposition 11.1.
$\mathrm {Diag}(u_1, u_2(-\pi _0)^b, u_3 (-\pi _0)^c)$ as in Proposition 11.1, it is proved by Proposition 11.1.
Case 2. When ![]() $L$ has a basis
$L$ has a basis ![]() $\{ {\bf x}_1, {\bf x}_2, {\bf x}_3\}$ whose Gram matrix is
$\{ {\bf x}_1, {\bf x}_2, {\bf x}_3\}$ whose Gram matrix is ![]() $T=\mathrm {Diag}( \mathcal {H}_a, u_3 (-\pi _0)^c)$, take
$T=\mathrm {Diag}( \mathcal {H}_a, u_3 (-\pi _0)^c)$, take ![]() $L^\flat = \text {Span}({\bf x}_1, {\bf x}_2)$ and
$L^\flat = \text {Span}({\bf x}_1, {\bf x}_2)$ and ![]() ${\bf x}={\bf x}_3$. By Propositions 11.1, 11.2 and 11.3, we have
${\bf x}={\bf x}_3$. By Propositions 11.1, 11.2 and 11.3, we have
for any ![]() $L^\flat \subset L^{\flat, \prime } \subset L^\flat _F$ (direct sums in the above identity are actually orthogonal direct sums). Thus, by Theorem 5.6(1) we have
$L^\flat \subset L^{\flat, \prime } \subset L^\flat _F$ (direct sums in the above identity are actually orthogonal direct sums). Thus, by Theorem 5.6(1) we have
Case 3. When ![]() $L$ has a Gram matrix
$L$ has a Gram matrix ![]() $\mathrm {Diag}(u_1 (-\pi _0)^a, u_2(-\pi _0)^b, u_3 (-\pi _0)^c)$ with
$\mathrm {Diag}(u_1 (-\pi _0)^a, u_2(-\pi _0)^b, u_3 (-\pi _0)^c)$ with ![]() $0\le a \le b \le c$, the same argument as Case 2 gives
$0\le a \le b \le c$, the same argument as Case 2 gives ![]() $\mathrm {Int}(L)=\partial \mathrm {Den}(L)$. This finishes the proof of the theorem.
$\mathrm {Int}(L)=\partial \mathrm {Den}(L)$. This finishes the proof of the theorem.
Theorems 1.2 and 5.6 imply the following corollary.
Corollary 11.4 For any lattice ![]() $L=L^\flat \oplus \mathcal {O}_F{\bf x} \subset \mathbb {V}$ of rank
$L=L^\flat \oplus \mathcal {O}_F{\bf x} \subset \mathbb {V}$ of rank ![]() $3$, we have
$3$, we have
12. Global applications
In this section we assume that ![]() $F$ is an imaginary quadratic field with discriminant
$F$ is an imaginary quadratic field with discriminant ![]() $d_F$. Denote by
$d_F$. Denote by ![]() $a\mapsto \bar a$ the complex conjugation on
$a\mapsto \bar a$ the complex conjugation on ![]() $F$. The result in this section can be easily extended to CM number fields (totally imaginary quadratic extension of a totally real number field) and more general level structures at split places, see [Reference Li and ZhangLZ22a] and [Reference He, Li, Shi and YangHLSY22]. We restrict to the imaginary quadratic fields to make the exposition as simple as possible.
$F$. The result in this section can be easily extended to CM number fields (totally imaginary quadratic extension of a totally real number field) and more general level structures at split places, see [Reference Li and ZhangLZ22a] and [Reference He, Li, Shi and YangHLSY22]. We restrict to the imaginary quadratic fields to make the exposition as simple as possible.
12.1 Unitary Shimura varieties and special cycles
In this subsection, we briefly review the definition of an integral model of Shimura variety defined in [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20] over ![]() $\mathrm {Spec}\, \mathcal {O}_F$ . Let
$\mathrm {Spec}\, \mathcal {O}_F$ . Let
be the algebraic stack which assigns to each ![]() $\mathcal {O}_F$-scheme
$\mathcal {O}_F$-scheme ![]() $S$ the groupoid of isomorphism classes of quadruples
$S$ the groupoid of isomorphism classes of quadruples ![]() $(A,\iota,\lambda,\mathcal {F}_A)$ where:
$(A,\iota,\lambda,\mathcal {F}_A)$ where:
(1)
 $A\rightarrow S$ is an abelian scheme of relative dimension
$A\rightarrow S$ is an abelian scheme of relative dimension  $n$;
$n$;(2)
 $\iota :\mathcal {O}_F\rightarrow \mathrm {End}(A)$ is an action satisfying the following determinant condition (the Kottwitz condition of signature
$\iota :\mathcal {O}_F\rightarrow \mathrm {End}(A)$ is an action satisfying the following determinant condition (the Kottwitz condition of signature  $(1,n-1)$)
for all
$(1,n-1)$)
for all \[ \mathrm{char}(T-\iota(\alpha)\mid \mathrm{Lie}\, A)=(T-s(\alpha)) (T-s(\bar{\alpha}))^{n-1} \in \mathcal{O}_S[T], \]
\[ \mathrm{char}(T-\iota(\alpha)\mid \mathrm{Lie}\, A)=(T-s(\alpha)) (T-s(\bar{\alpha}))^{n-1} \in \mathcal{O}_S[T], \]
 $\alpha \in \mathcal {O}_F$ where
$\alpha \in \mathcal {O}_F$ where  $s:\mathcal {O}_F\rightarrow \mathcal {O}_S$ is the structure morphism;
$s:\mathcal {O}_F\rightarrow \mathcal {O}_S$ is the structure morphism;(3)
 $\lambda :A\rightarrow A^\vee$ is a principal polarization whose Rosati involution satisfies
$\lambda :A\rightarrow A^\vee$ is a principal polarization whose Rosati involution satisfies  $\iota (\alpha )^*=\iota (\bar {\alpha })$ for all
$\iota (\alpha )^*=\iota (\bar {\alpha })$ for all  $\alpha \in \mathcal {O}_F$;
$\alpha \in \mathcal {O}_F$;(4)
 $\mathcal {F}_A \subset \mathrm {Lie}\, A$ is an
$\mathcal {F}_A \subset \mathrm {Lie}\, A$ is an  $\mathcal {O}_F$-stable
$\mathcal {O}_F$-stable  $\mathcal {O}_S$-module local direct summand of rank
$\mathcal {O}_S$-module local direct summand of rank  $n-1$ satisfying the Krämer condition;
$n-1$ satisfying the Krämer condition;  $\mathcal {O}_F$ acts on
$\mathcal {O}_F$ acts on  $\mathrm {Lie}\, A/\mathcal {F}_A$ by the structure map
$\mathrm {Lie}\, A/\mathcal {F}_A$ by the structure map  $s:\mathcal {O}_F \rightarrow \mathcal {O}_S$ and acts on
$s:\mathcal {O}_F \rightarrow \mathcal {O}_S$ and acts on  $\mathcal {F}_A$ by the complex conjugate of the structure map.
$\mathcal {F}_A$ by the complex conjugate of the structure map.
Two objects ![]() $(A,\iota,\lambda,\mathcal {F}_A)$ and
$(A,\iota,\lambda,\mathcal {F}_A)$ and ![]() $(A',\iota ',\lambda ',\mathcal {F}_{A'})$ in
$(A',\iota ',\lambda ',\mathcal {F}_{A'})$ in ![]() $\mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}(S)$ are isomorphic if there is an
$\mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}(S)$ are isomorphic if there is an ![]() $\mathcal {O}_F$-linear isomorphism
$\mathcal {O}_F$-linear isomorphism ![]() $f:A\rightarrow A'$ of abelian schemes such that
$f:A\rightarrow A'$ of abelian schemes such that ![]() $f^*(\lambda ')=\lambda$ and
$f^*(\lambda ')=\lambda$ and ![]() $f_*(\mathcal {F}_A)=\mathcal {F}_{A'}$. The stack
$f_*(\mathcal {F}_A)=\mathcal {F}_{A'}$. The stack ![]() $\mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}$ is flat of dimension
$\mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}$ is flat of dimension ![]() $n-1$ over
$n-1$ over ![]() $\mathrm {Spec}\, \mathcal {O}_F$. It is smooth over
$\mathrm {Spec}\, \mathcal {O}_F$. It is smooth over ![]() $\mathrm {Spec}\, \mathcal {O}_F[{1}/{{d_F}}]$ and has semi-stable reduction over primes of
$\mathrm {Spec}\, \mathcal {O}_F[{1}/{{d_F}}]$ and has semi-stable reduction over primes of ![]() $F$ dividing
$F$ dividing ![]() ${d_F}$. This is indicated by the corresponding behaviour of its local model studied in [Reference KrämerKrä03]. Analogously one can define
${d_F}$. This is indicated by the corresponding behaviour of its local model studied in [Reference KrämerKrä03]. Analogously one can define ![]() $\mathcal {M}_{(0,1)}\rightarrow \mathcal {O}_F$ be the algebraic stack which assigns to each
$\mathcal {M}_{(0,1)}\rightarrow \mathcal {O}_F$ be the algebraic stack which assigns to each ![]() $\mathcal {O}_F$-scheme
$\mathcal {O}_F$-scheme ![]() $S$ the groupoid of isomorphism classes of triples
$S$ the groupoid of isomorphism classes of triples ![]() $(E,\iota _0,\lambda _0)$ where:
$(E,\iota _0,\lambda _0)$ where:
(1)
 $E\rightarrow S$ is an abelian scheme of relative dimension
$E\rightarrow S$ is an abelian scheme of relative dimension  $1$;
$1$;(2)
 $\iota _0:\mathcal {O}_F\rightarrow \mathrm {End}(E)$ is an action such that its induced action on
$\iota _0:\mathcal {O}_F\rightarrow \mathrm {End}(E)$ is an action such that its induced action on  $\mathrm {Lie}\, E$ agrees with the complex conjugate of the structural map
$\mathrm {Lie}\, E$ agrees with the complex conjugate of the structural map  $s:\mathcal {O}_F\rightarrow \mathcal {O}_S$;
$s:\mathcal {O}_F\rightarrow \mathcal {O}_S$;(3)
 $\lambda _0:E\rightarrow E^\vee$ is a principal polarization whose Rosati involution satisfies
$\lambda _0:E\rightarrow E^\vee$ is a principal polarization whose Rosati involution satisfies  $\iota _0(\alpha )^*=\iota _0(\bar {\alpha })$ for all
$\iota _0(\alpha )^*=\iota _0(\bar {\alpha })$ for all  $\alpha \in \mathcal {O}_F$.
$\alpha \in \mathcal {O}_F$.
The stack ![]() $\mathcal {M}_{(0,1)}$ is smooth of relative dimension
$\mathcal {M}_{(0,1)}$ is smooth of relative dimension ![]() $0$ over
$0$ over ![]() $\mathrm {Spec}\, \mathcal {O}_F$, see, for example, [Reference HowardHow15, Proposition 2.1.2].
$\mathrm {Spec}\, \mathcal {O}_F$, see, for example, [Reference HowardHow15, Proposition 2.1.2].
Assume that ![]() $\mathbb {F}$ is an algebraically closed field of characteristic
$\mathbb {F}$ is an algebraically closed field of characteristic ![]() $p$ over
$p$ over ![]() $\mathcal {O}_F$. Let
$\mathcal {O}_F$. Let
For any prime number ![]() $\ell \neq p$, we can define a Hermitian form
$\ell \neq p$, we can define a Hermitian form ![]() $h(x,y)$ on the Tate module
$h(x,y)$ on the Tate module
as in [Reference Kudla and RapoportKR14b, § 2.3] using the polarizations ![]() $\lambda _0,\lambda$ and Weil pairings on
$\lambda _0,\lambda$ and Weil pairings on ![]() $E_0,A$.
$E_0,A$.
Fix a Hermitian space ![]() $W$ over
$W$ over ![]() $F$ of signature
$F$ of signature ![]() $(1,n-1)$ that contains a self-dual lattice
$(1,n-1)$ that contains a self-dual lattice ![]() $\mathfrak {a}$ and a Hermitian space
$\mathfrak {a}$ and a Hermitian space ![]() $W_0$ over
$W_0$ over ![]() $F$ of signature
$F$ of signature ![]() $(0,1)$ that contains a self-dual lattice
$(0,1)$ that contains a self-dual lattice ![]() $\mathfrak {a}_0$. Define
$\mathfrak {a}_0$. Define
Here ![]() $V$ and
$V$ and ![]() $L$ are equipped with Hermitian forms coming from those on
$L$ are equipped with Hermitian forms coming from those on ![]() $W_0$ and
$W_0$ and ![]() $W$. Define
$W$. Define ![]() $G:=\mathrm {U}(W)$. Also define the group scheme
$G:=\mathrm {U}(W)$. Also define the group scheme ![]() $\mathrm {GU}(W)$ over
$\mathrm {GU}(W)$ over ![]() $\mathbb {Q}$ by
$\mathbb {Q}$ by
where ![]() $R$ is any
$R$ is any ![]() $\mathbb {Q}$-algebra. Also define
$\mathbb {Q}$-algebra. Also define ![]() $Z:=\mathrm {Res}_{F/\mathbb {Q}} \mathbb {G}_m=\mathrm {GU}(W_0)$ and
$Z:=\mathrm {Res}_{F/\mathbb {Q}} \mathbb {G}_m=\mathrm {GU}(W_0)$ and
where the maps from the factors on the right-hand side to ![]() $\mathbb {G}_m$ are
$\mathbb {G}_m$ are ![]() $\mathrm {Nm}_{F/\mathbb {Q}}$ and the similitude character
$\mathrm {Nm}_{F/\mathbb {Q}}$ and the similitude character ![]() $c(g)$, respectively. We have an isomorphism of group schemes
$c(g)$, respectively. We have an isomorphism of group schemes
Let ![]() $K_G$ be the compact subgroup of
$K_G$ be the compact subgroup of ![]() $G(\mathbb {A}_f)$ that stabilizes the lattice
$G(\mathbb {A}_f)$ that stabilizes the lattice ![]() $\mathfrak {a}\otimes \hat {\mathbb {Z}}$ and
$\mathfrak {a}\otimes \hat {\mathbb {Z}}$ and ![]() $K_Z=\hat {\mathbb {Z}}^\times \subset Z(\mathbb {A}_f)$. Under the isomorphism (12.4), define
$K_Z=\hat {\mathbb {Z}}^\times \subset Z(\mathbb {A}_f)$. Under the isomorphism (12.4), define
Now define ![]() $\mathcal {M}\subset \mathcal {M}_{(0,1)}\times \mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}$ to be the open and closed substack such that
$\mathcal {M}\subset \mathcal {M}_{(0,1)}\times \mathcal {M}^{\mathrm {Kra}}_{(1,n-1)}$ to be the open and closed substack such that
if and only if there is an isomorphism of Hermitian ![]() $\mathcal {O}_F\otimes \mathbb {Z}_\ell$-modules
$\mathcal {O}_F\otimes \mathbb {Z}_\ell$-modules
for any geometric point ![]() $s\in S$ and prime
$s\in S$ and prime ![]() $\ell$ that is not the same as the characteristic of
$\ell$ that is not the same as the characteristic of ![]() $s$. Then
$s$. Then ![]() $\mathcal {M}$ is an integral model of the Shimura variety associated to the group
$\mathcal {M}$ is an integral model of the Shimura variety associated to the group ![]() $\tilde {G}$ with level structure defined by
$\tilde {G}$ with level structure defined by ![]() $K$.
$K$.
Now we review the definition of special cycles. For ![]() $(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A)\in \mathcal {M}(S)$ where
$(E,\iota _0,\lambda _0, A,\iota, \lambda,\mathcal {F}_A)\in \mathcal {M}(S)$ where ![]() $S$ is an
$S$ is an ![]() $\mathcal {O}_F$-scheme, consider the projective
$\mathcal {O}_F$-scheme, consider the projective ![]() $\mathcal {O}_F$-module of finite rank
$\mathcal {O}_F$-module of finite rank
On this module there is a Hermitian form ![]() $h'(x,y)$ defined by
$h'(x,y)$ defined by
where ![]() $y^\vee$ is the dual homomorphism of
$y^\vee$ is the dual homomorphism of ![]() $y$. It is proved in [Reference Kudla and RapoportKR14b, Lemma 2.7] that
$y$. It is proved in [Reference Kudla and RapoportKR14b, Lemma 2.7] that ![]() $h'(x,y)$ is positive semi-definite. The following is [Reference Kudla and RapoportKR14b, Definition 2.8].
$h'(x,y)$ is positive semi-definite. The following is [Reference Kudla and RapoportKR14b, Definition 2.8].
Definition 12.1 For ![]() $T\in \mathrm {Herm}_m(\mathbb {Z})_{>0}$, the special cycle
$T\in \mathrm {Herm}_m(\mathbb {Z})_{>0}$, the special cycle ![]() $\mathcal {Z}(T)$ is the stack of collections
$\mathcal {Z}(T)$ is the stack of collections ![]() $(E,\iota _0,\lambda _0,A,\iota,\lambda,\mathcal {F}_A,{\bf x})$ where
$(E,\iota _0,\lambda _0,A,\iota,\lambda,\mathcal {F}_A,{\bf x})$ where
and ![]() ${\bf x}=(x_1,\ldots,x_m)\in \mathrm {Hom}_{\mathcal {O}_F}(E,A)^m$ such that
${\bf x}=(x_1,\ldots,x_m)\in \mathrm {Hom}_{\mathcal {O}_F}(E,A)^m$ such that
When ![]() $t\in \mathbb {Z}_{>0}$, each component of
$t\in \mathbb {Z}_{>0}$, each component of ![]() $\mathcal {Z}(t)$ is a divisor by [Reference HowardHow15, Proposition 3.2.3]. In general,
$\mathcal {Z}(t)$ is a divisor by [Reference HowardHow15, Proposition 3.2.3]. In general, ![]() $\mathcal {Z}(T)$ does not necessarily have the expected codimension which is the rank of
$\mathcal {Z}(T)$ does not necessarily have the expected codimension which is the rank of ![]() $T$.
$T$.
Let ![]() $\mathcal {C} =\{ \mathcal {C}_p\}$ be a incoherent collection of local Hermitian spaces of rank
$\mathcal {C} =\{ \mathcal {C}_p\}$ be a incoherent collection of local Hermitian spaces of rank ![]() $n$ such that
$n$ such that ![]() $\mathcal {C}_\ell \cong V_\ell$ for all finite
$\mathcal {C}_\ell \cong V_\ell$ for all finite ![]() $\ell$ and
$\ell$ and ![]() $\mathcal {C}_\infty$ is positive definite. For a non-singular Hermitian matrix
$\mathcal {C}_\infty$ is positive definite. For a non-singular Hermitian matrix ![]() $T$ of rank
$T$ of rank ![]() $n$ with values in
$n$ with values in ![]() $\mathcal {O}_F$, Let
$\mathcal {O}_F$, Let ![]() $V_T$ be the Hermitian space with Gram matrix
$V_T$ be the Hermitian space with Gram matrix ![]() $T$. Define
$T$. Define
Then ![]() $\mathrm {Diff}(T,\mathcal {C})$ is a finite set consisting of places of
$\mathrm {Diff}(T,\mathcal {C})$ is a finite set consisting of places of ![]() $\mathbb {Q}$ inert or ramified in
$\mathbb {Q}$ inert or ramified in ![]() $F$. By [Reference Kudla and RapoportKR14b, Proposition 2.22],
$F$. By [Reference Kudla and RapoportKR14b, Proposition 2.22], ![]() $\mathcal {Z}(T)$ is empty if
$\mathcal {Z}(T)$ is empty if ![]() $|\mathrm {Diff}(T,\mathcal {C})|>1$. If
$|\mathrm {Diff}(T,\mathcal {C})|>1$. If ![]() $\mathrm {Diff}(T,\mathcal {C})=\{p\}$ for a finite prime
$\mathrm {Diff}(T,\mathcal {C})=\{p\}$ for a finite prime ![]() $p$ inert or ramified in
$p$ inert or ramified in ![]() $F$, it is proved in [Reference Kudla and RapoportKR14b] that the support of
$F$, it is proved in [Reference Kudla and RapoportKR14b] that the support of ![]() $\mathcal {Z}(T)$ is on the supersingular locus of
$\mathcal {Z}(T)$ is on the supersingular locus of ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathrm {Spec}\, \bar {\mathbb {F}}_p$. Let
$\mathrm {Spec}\, \bar {\mathbb {F}}_p$. Let ![]() $e$ be the ramification index of
$e$ be the ramification index of ![]() $F_p/\mathbb {Q}_p$. Define the arithmetic degree
$F_p/\mathbb {Q}_p$. Define the arithmetic degree
where ![]() $\otimes ^\mathbb {L}$ denotes the derived tensor product on the category of coherent sheaves on
$\otimes ^\mathbb {L}$ denotes the derived tensor product on the category of coherent sheaves on ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $\chi$ is Euler characteristic and
$\chi$ is Euler characteristic and ![]() $t_i$ (
$t_i$ (![]() $1 \le i \le n$) are the diagonal entries of
$1 \le i \le n$) are the diagonal entries of ![]() $T$. When
$T$. When ![]() $\mathrm {Diff}(T,\mathcal {C})=\{\infty \}$,
$\mathrm {Diff}(T,\mathcal {C})=\{\infty \}$, ![]() $\mathcal {Z}(T)$ is empty [Reference Kudla and RapoportKR14b, Lemma 2.7] and the arithmetic degree
$\mathcal {Z}(T)$ is empty [Reference Kudla and RapoportKR14b, Lemma 2.7] and the arithmetic degree ![]() $\widehat {\mathrm {deg}}_T(v)$ is the integration of a green current
$\widehat {\mathrm {deg}}_T(v)$ is the integration of a green current ![]() $G(T, v)$ (
$G(T, v)$ (![]() $v >0$ is a positive-definite Hermitian matrix of order
$v >0$ is a positive-definite Hermitian matrix of order ![]() $n$) defined by Liu [Reference LiuLiu11] and Garcia and Sankaran [Reference Garcia and SankaranGS19]; see, for example, [Reference Li and ZhangLZ22a, Equation (15.3.0.2)].
$n$) defined by Liu [Reference LiuLiu11] and Garcia and Sankaran [Reference Garcia and SankaranGS19]; see, for example, [Reference Li and ZhangLZ22a, Equation (15.3.0.2)].
12.2 Eisenstein series
On the analytic side, let ![]() $\chi :\mathbb {A}/\mathbb {Q}^\times \rightarrow \mathbb {C}^\times$ be the quadratic character associated to the extension
$\chi :\mathbb {A}/\mathbb {Q}^\times \rightarrow \mathbb {C}^\times$ be the quadratic character associated to the extension ![]() $F/\mathbb {Q}$. Fix a character
$F/\mathbb {Q}$. Fix a character ![]() $\eta :\mathbb {A}_F^\times \rightarrow \mathbb {C}^\times$ such that
$\eta :\mathbb {A}_F^\times \rightarrow \mathbb {C}^\times$ such that ![]() $\eta |_{\mathbb {A}^\times }=\chi ^n$. We consider an incoherent Eisenstein series
$\eta |_{\mathbb {A}^\times }=\chi ^n$. We consider an incoherent Eisenstein series ![]() $E(z,s,\Phi )$ associated to a section
$E(z,s,\Phi )$ associated to a section ![]() $\Phi =\otimes \Phi _p$ in a degenerate principal series representation
$\Phi =\otimes \Phi _p$ in a degenerate principal series representation ![]() $I(s, \eta )$ of
$I(s, \eta )$ of ![]() $\mathrm {U}(n,n)(\mathbb {A})$ (see [Reference Li and ZhangLZ22a, § 12] or [Reference Kudla and RapoportKR14b]), where
$\mathrm {U}(n,n)(\mathbb {A})$ (see [Reference Li and ZhangLZ22a, § 12] or [Reference Kudla and RapoportKR14b]), where ![]() $\tau \in \mathbb {H}_n$ (see (1.18)),
$\tau \in \mathbb {H}_n$ (see (1.18)), ![]() $s\in \mathbb {C}$ and
$s\in \mathbb {C}$ and ![]() $\Phi _p$ is given as follows. The section
$\Phi _p$ is given as follows. The section ![]() $\Phi _\infty$ is the standard weight
$\Phi _\infty$ is the standard weight ![]() $n$ section. When
$n$ section. When ![]() $p < \infty$ is unramified in
$p < \infty$ is unramified in ![]() $F$,
$F$, ![]() $\Phi _p$ is the standard section associated to the characteristic function of
$\Phi _p$ is the standard section associated to the characteristic function of ![]() $L_p^n$ via the map
$L_p^n$ via the map ![]() $\lambda : S(\mathcal {C}_p^n) \rightarrow I(0, \eta _p)$:
$\lambda : S(\mathcal {C}_p^n) \rightarrow I(0, \eta _p)$:
where ![]() $\omega$ is the Weil representation of
$\omega$ is the Weil representation of ![]() $\mathrm {U}(n,n)$ associated to the character
$\mathrm {U}(n,n)$ associated to the character ![]() $\chi$. When
$\chi$. When ![]() $p$ is ramified in
$p$ is ramified in ![]() $F$, define
$F$, define
 \begin{equation} \Phi_{p}=\Phi_p^0+\sum_{i=1}^{\lfloor {n}/{2}\rfloor} A_{p,\epsilon}^i(s) \cdot \Phi_p^i. \end{equation}
\begin{equation} \Phi_{p}=\Phi_p^0+\sum_{i=1}^{\lfloor {n}/{2}\rfloor} A_{p,\epsilon}^i(s) \cdot \Phi_p^i. \end{equation}
Here ![]() $\Phi _p^0$ is the standard section associated to the characteristic function
$\Phi _p^0$ is the standard section associated to the characteristic function ![]() $L_p^n$,
$L_p^n$, ![]() $\Phi _p^i$ is the standard section associated to the characteristic function of
$\Phi _p^i$ is the standard section associated to the characteristic function of ![]() $(\mathcal {H}_{n,i}^{\epsilon })^n$ at
$(\mathcal {H}_{n,i}^{\epsilon })^n$ at ![]() $p$ with
$p$ with ![]() $\epsilon =-\chi _p(L_p)$, and
$\epsilon =-\chi _p(L_p)$, and
where ![]() $c_{n,i}^\epsilon$ are as in (1.9). Let
$c_{n,i}^\epsilon$ are as in (1.9). Let ![]() $\psi$ be the standard additive character of
$\psi$ be the standard additive character of ![]() $\mathbb {A}/\mathbb {Q}$, i.e.
$\mathbb {A}/\mathbb {Q}$, i.e.
where ![]() $\lambda$ is the canonical map
$\lambda$ is the canonical map ![]() $\mathbb {Q}_\ell \rightarrow \mathbb {Q}_\ell /\mathbb {Z}_\ell \hookrightarrow \mathbb {Q}/\mathbb {Z}$. Let
$\mathbb {Q}_\ell \rightarrow \mathbb {Q}_\ell /\mathbb {Z}_\ell \hookrightarrow \mathbb {Q}/\mathbb {Z}$. Let ![]() $E_T(\tau,s,\Phi )$ (respectively,
$E_T(\tau,s,\Phi )$ (respectively, ![]() $E'_T(\tau,\Phi )$) be the
$E'_T(\tau,\Phi )$) be the ![]() $T$th Fourier coefficient of
$T$th Fourier coefficient of ![]() $E(\tau,s,\Phi )$ (respectively,
$E(\tau,s,\Phi )$ (respectively, ![]() $E'(\tau, 0, \Phi )$) with respect to
$E'(\tau, 0, \Phi )$) with respect to ![]() $\psi$. Then, for
$\psi$. Then, for ![]() $s\gg 0$, we have the following product formula (see, for example, [Reference Li and ZhangLZ22a, § 12.4]):
$s\gg 0$, we have the following product formula (see, for example, [Reference Li and ZhangLZ22a, § 12.4]):
where ![]() $c_\infty$ is a constant independent of
$c_\infty$ is a constant independent of ![]() $T$ calculated in [Reference LiuLiu11, Proposition 4.5], and
$T$ calculated in [Reference LiuLiu11, Proposition 4.5], and ![]() $W_{T,p}(1,s,\Phi _p)$ is the local Whittaker integral defined in [Reference Kudla and RapoportKR14b, Equation (10.2)].
$W_{T,p}(1,s,\Phi _p)$ is the local Whittaker integral defined in [Reference Kudla and RapoportKR14b, Equation (10.2)].
12.3 An equivalent form of Conjecture 1.1
In this subsection we assume ![]() $p$ is a prime of
$p$ is a prime of ![]() $\mathbb {Q}$ ramified in
$\mathbb {Q}$ ramified in ![]() $F$. Let
$F$. Let ![]() $|\cdot |_p$ be the non-Archimedean valuation on
$|\cdot |_p$ be the non-Archimedean valuation on ![]() $F_p$ normalized so that
$F_p$ normalized so that ![]() $|\sqrt {d_F}|_p={1}/{p}$. For
$|\sqrt {d_F}|_p={1}/{p}$. For ![]() $\epsilon =\pm 1$, let
$\epsilon =\pm 1$, let ![]() $V_{p}^{\epsilon }$ be the (unique up to isomorphism)
$V_{p}^{\epsilon }$ be the (unique up to isomorphism) ![]() $F_p/\mathbb {Q}_p$-Hermitian space of dimension
$F_p/\mathbb {Q}_p$-Hermitian space of dimension ![]() $n$ and sign
$n$ and sign ![]() $\epsilon$. For any lattice
$\epsilon$. For any lattice ![]() $M_p$ of rank
$M_p$ of rank ![]() $n$ in
$n$ in ![]() $V_p^\epsilon$, let
$V_p^\epsilon$, let ![]() $\Phi _{M_p}\in I_p(s,\eta _p)$ be the standard section associated to the characteristic function of
$\Phi _{M_p}\in I_p(s,\eta _p)$ be the standard section associated to the characteristic function of ![]() $M_p^n$. By [Reference ShiShi22, Proposition 9.7], we have
$M_p^n$. By [Reference ShiShi22, Proposition 9.7], we have
where ![]() $f=\tfrac {1}{2}n^2+\tfrac {1}{4}n(n-1)$,
$f=\tfrac {1}{2}n^2+\tfrac {1}{4}n(n-1)$, ![]() $\alpha _p(\cdot,\cdot,X)$ is the local density polynomial defined in (5.1) at the place
$\alpha _p(\cdot,\cdot,X)$ is the local density polynomial defined in (5.1) at the place ![]() $p$ and
$p$ and ![]() $\gamma _p(V_{p}^{\epsilon })$ is an
$\gamma _p(V_{p}^{\epsilon })$ is an ![]() $8$th root of unity defined in [Reference Kudla and RapoportKR14b, Equation (10.3)]. By [Reference Kudla and RapoportKR14b], we know
$8$th root of unity defined in [Reference Kudla and RapoportKR14b, Equation (10.3)]. By [Reference Kudla and RapoportKR14b], we know
For ![]() $T\in \mathrm {Herm}_n(F)$, choose a lattice
$T\in \mathrm {Herm}_n(F)$, choose a lattice ![]() $L_T$ in the Hermitian space
$L_T$ in the Hermitian space ![]() $V_{p}^{\chi _p(T)}$ with Gram matrix
$V_{p}^{\chi _p(T)}$ with Gram matrix ![]() $T$. Then (12.14) and (12.15) imply that Conjecture 1.1 at the place
$T$. Then (12.14) and (12.15) imply that Conjecture 1.1 at the place ![]() $p$ is equivalent to the following conjecture.
$p$ is equivalent to the following conjecture.
Conjecture 12.2 Let ![]() $\mathbb {V}$ be the space of special quasi-homomorphisms as in (1.2) such that
$\mathbb {V}$ be the space of special quasi-homomorphisms as in (1.2) such that ![]() $\chi _p(\mathbb {V}) =\epsilon$. Let
$\chi _p(\mathbb {V}) =\epsilon$. Let ![]() $T\in \mathrm {Herm}_n(F)$ such that
$T\in \mathrm {Herm}_n(F)$ such that ![]() $\chi _p(T)=\epsilon$ and
$\chi _p(T)=\epsilon$ and ![]() $L_T$ be a lattice of rank
$L_T$ be a lattice of rank ![]() $n$ in
$n$ in ![]() $\mathbb {V}$ with Gram matrix
$\mathbb {V}$ with Gram matrix ![]() $T$. Then
$T$. Then
 \[ \mathrm{Int}(L_T)\cdot \log p= \frac{W'_{T,p}(1,0,\Phi_p)}{W_{I_n^{-\epsilon},p}(1,0,\Phi_p)}, \]
\[ \mathrm{Int}(L_T)\cdot \log p= \frac{W'_{T,p}(1,0,\Phi_p)}{W_{I_n^{-\epsilon},p}(1,0,\Phi_p)}, \]
where ![]() $\Phi _p$ is defined in (12.10).
$\Phi _p$ is defined in (12.10).
12.4 (Global) arithmetic Siegel–Weil formula
Similar to [Reference Li and ZhangLZ22a, Theorem 1.3.1], we have the following theorem.
Theorem 12.3 (Arithmetic Siegel–Weil formula for non-singular coefficients)
Assume that the fundamental discriminant of ![]() $F$ is
$F$ is ![]() $d_F \equiv 1 \pmod 8$ and that Conjecture 1.1 holds for every
$d_F \equiv 1 \pmod 8$ and that Conjecture 1.1 holds for every ![]() $F_p$ with
$F_p$ with ![]() $p|d_F$. For any non-singular Hermitian matrix
$p|d_F$. For any non-singular Hermitian matrix ![]() $T$ with values in
$T$ with values in ![]() $\mathcal {O}_F$ of size
$\mathcal {O}_F$ of size ![]() $n$, we have
$n$, we have
where ![]() $C$ is an explicit constant that only depends on
$C$ is an explicit constant that only depends on ![]() $F$ and
$F$ and ![]() $L$,
$L$, ![]() $\widehat {\mathrm {deg}}_{T}(v)=\widehat {\mathrm {deg}}_{T}$ for positive-definite
$\widehat {\mathrm {deg}}_{T}(v)=\widehat {\mathrm {deg}}_{T}$ for positive-definite ![]() $T$, and
$T$, and ![]() $\tau =u + i v$. In particular, the arithmetic Siegel–Weil formula holds for
$\tau =u + i v$. In particular, the arithmetic Siegel–Weil formula holds for ![]() $n=2, 3$ for non-singular
$n=2, 3$ for non-singular ![]() $T$.
$T$.
Proof. We sketch the main idea of the proof. When ![]() $|\text {Diff}(T, \mathcal {C})| >1$, both sides are zero. When
$|\text {Diff}(T, \mathcal {C})| >1$, both sides are zero. When ![]() $\text {Diff}(T, \mathcal {C}) =\{ p\}$ for a finite prime
$\text {Diff}(T, \mathcal {C}) =\{ p\}$ for a finite prime ![]() $p\ne 2$ (as
$p\ne 2$ (as ![]() $d_F \equiv 1 \pmod 8$), then
$d_F \equiv 1 \pmod 8$), then ![]() $T$ is positive definite and the support of
$T$ is positive definite and the support of ![]() $\mathcal {Z}(T)$ is on the supersingular locus of
$\mathcal {Z}(T)$ is on the supersingular locus of ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathrm {Spec}\, \bar {\mathbb {F}}_p$ although it has higher than expected dimension and needs ‘derivation’ to make it correct dimensional cycle (we skip it here and just define its degree in the following). When
$\mathrm {Spec}\, \bar {\mathbb {F}}_p$ although it has higher than expected dimension and needs ‘derivation’ to make it correct dimensional cycle (we skip it here and just define its degree in the following). When ![]() $p$ is inert in
$p$ is inert in ![]() $F$, the theorem is proved in [Reference Li and ZhangLZ22a, Theorem 1.3.1]. When
$F$, the theorem is proved in [Reference Li and ZhangLZ22a, Theorem 1.3.1]. When ![]() $p$ is ramified in
$p$ is ramified in ![]() $F$, the theorem can be proved in a similar fashion assuming Conjecture 1.1. The key is that by the
$F$, the theorem can be proved in a similar fashion assuming Conjecture 1.1. The key is that by the ![]() $p$-adic uniformization theorem [Reference Rapoport and ZinkRZ96, Chapter 6], for each component
$p$-adic uniformization theorem [Reference Rapoport and ZinkRZ96, Chapter 6], for each component ![]() $\mathcal {Z}$ of
$\mathcal {Z}$ of ![]() ${Z}(T) (\bar {\mathbb {F}}_p)$, the arithmetic degree of
${Z}(T) (\bar {\mathbb {F}}_p)$, the arithmetic degree of ![]() $\mathcal {Z}(T)$ supported on
$\mathcal {Z}(T)$ supported on ![]() $\mathcal {Z}$
$\mathcal {Z}$
is the same as ![]() $\mathrm {Int}(L) \log p$ (
$\mathrm {Int}(L) \log p$ (![]() $L$ has Gram matrix
$L$ has Gram matrix ![]() $T$) in Conjecture 1.1. In particular, this number is independent of the choice of
$T$) in Conjecture 1.1. In particular, this number is independent of the choice of ![]() $\mathcal {Z}$ and depends only on
$\mathcal {Z}$ and depends only on ![]() $T$. Assuming that Conjecture 1.1 (or rather its equivalent form Conjecture 12.2) holds, this is then equal to
$T$. Assuming that Conjecture 1.1 (or rather its equivalent form Conjecture 12.2) holds, this is then equal to ![]() $c_{p, 1} W_{T, p}'(1, 0, \Phi _p)$ for some constant
$c_{p, 1} W_{T, p}'(1, 0, \Phi _p)$ for some constant ![]() $c_{p, 1}\ne 0$. Thus,
$c_{p, 1}\ne 0$. Thus, ![]() $\widehat {\mathrm {deg}}_T$ is this number times the number of components of
$\widehat {\mathrm {deg}}_T$ is this number times the number of components of ![]() ${Z}(T)(\bar {\mathbb {F}}_p)$, which can be counted via the Siegel–Weil formula. Combining these results together with (12.13), we can prove
${Z}(T)(\bar {\mathbb {F}}_p)$, which can be counted via the Siegel–Weil formula. Combining these results together with (12.13), we can prove
for come explicit constant ![]() $C_p$ independent of
$C_p$ independent of ![]() $T$. Similar argument holds when
$T$. Similar argument holds when ![]() $\text {Diff}(T, \mathcal {C}) =\{ \infty \}$ in which case the theorem is proved in [Reference LiuLiu11] and [Reference Garcia and SankaranGS19]. Finally, one checks that
$\text {Diff}(T, \mathcal {C}) =\{ \infty \}$ in which case the theorem is proved in [Reference LiuLiu11] and [Reference Garcia and SankaranGS19]. Finally, one checks that ![]() $C_p$ is independent of the choice of
$C_p$ is independent of the choice of ![]() $p$.
$p$.
Acknowledgements
We thank C. Li for his help during the preparation of this paper. We thank the referees for their careful reading of the paper and their comments which make the paper more readable.
Conflicts of Interest
None.
Appendix A Calculation of primitive local density
In this appendix, we provide the proofs of Propositions 5.9 and 5.10. Throughout this section, ![]() $M$ is unimodular of rank
$M$ is unimodular of rank ![]() $m\ge 2$ unless clearly stated otherwise. Let
$m\ge 2$ unless clearly stated otherwise. Let ![]() $\{ v_1, \ldots, v_{2k}, v_{2k+1}, \ldots, v_{2k+m}\}$ be a basis of
$\{ v_1, \ldots, v_{2k}, v_{2k+1}, \ldots, v_{2k+m}\}$ be a basis of ![]() $M^{[k]}=\mathcal {H}^k{\unicode{x29BA}} M$ with Gram matrix
$M^{[k]}=\mathcal {H}^k{\unicode{x29BA}} M$ with Gram matrix ![]() $\mathcal {H}^k{\unicode{x29BA}} \mathrm {Diag}(I_{m-1}, \nu )$. Let
$\mathcal {H}^k{\unicode{x29BA}} \mathrm {Diag}(I_{m-1}, \nu )$. Let ![]() $L$ be a Hermitian lattice of rank
$L$ be a Hermitian lattice of rank ![]() $n$ with Gram matrix
$n$ with Gram matrix ![]() $T$. An isometric embedding
$T$. An isometric embedding ![]() $\varphi :L\to M$ is called primitive if its image in
$\varphi :L\to M$ is called primitive if its image in ![]() $M/\pi M$ has dimension
$M/\pi M$ has dimension ![]() $\mathrm {rank}_{\mathcal {O}_F} (L)$. We call a vector
$\mathrm {rank}_{\mathcal {O}_F} (L)$. We call a vector ![]() $v$ primitive in
$v$ primitive in ![]() $M$ if
$M$ if ![]() $\pi ^{-1}v \not \in M$ or, equivalently, the natural embedding
$\pi ^{-1}v \not \in M$ or, equivalently, the natural embedding ![]() $\varphi :\mathrm {Span_{\mathcal {O}_F}}\{v\}\hookrightarrow M$ is primitive. For a
$\varphi :\mathrm {Span_{\mathcal {O}_F}}\{v\}\hookrightarrow M$ is primitive. For a ![]() $v\in M^{[k]}$, we let
$v\in M^{[k]}$, we let ![]() $\Pr _{\mathcal {H}^k}(w_i)$ be the projection of
$\Pr _{\mathcal {H}^k}(w_i)$ be the projection of ![]() $w_i$ to
$w_i$ to ![]() $\mathcal {H}^{k}$.
$\mathcal {H}^{k}$.
A.1 Proof of Proposition 5.9
The main purpose of this subsection is to prove the first four parts of Proposition 5.9. Part (5) of this proposition follows from Proposition 5.7 and Corollaries A.10 and A.12.
Proof. For part (1), choose ![]() $M(1)=({t\pi }/{2})v_1+v_2 \in M^{[k]}$ with
$M(1)=({t\pi }/{2})v_1+v_2 \in M^{[k]}$ with ![]() $q(M(1))=t$. Then
$q(M(1))=t$. Then
 \begin{align} M(1)^{\perp}&=\mathrm{Span_{\mathcal{O}_F}}\biggl\{\frac{-t\pi }{2}v_1+v_2,v_3,\ldots,v_{2k}, v_{2k+1}, \ldots, v_{2k+m}\biggr\}\nonumber\\ &\cong \langle -t \rangle {\unicode{x29BA}} \mathcal{H}^{k-1} {\unicode{x29BA}} M , \end{align}
\begin{align} M(1)^{\perp}&=\mathrm{Span_{\mathcal{O}_F}}\biggl\{\frac{-t\pi }{2}v_1+v_2,v_3,\ldots,v_{2k}, v_{2k+1}, \ldots, v_{2k+m}\biggr\}\nonumber\\ &\cong \langle -t \rangle {\unicode{x29BA}} \mathcal{H}^{k-1} {\unicode{x29BA}} M , \end{align}
which is represented by ![]() $\mathrm {Diag}(-t, \mathcal {H}^{k-1}, S)$. It is easy to check
$\mathrm {Diag}(-t, \mathcal {H}^{k-1}, S)$. It is easy to check
For parts (2) and (3), assume first that ![]() $M$ is isotropic (and unimodular). In this case, we may choose a basis
$M$ is isotropic (and unimodular). In this case, we may choose a basis ![]() $\{v_{2k+1}',\ldots,v_{2k+m}'\}$ of
$\{v_{2k+1}',\ldots,v_{2k+m}'\}$ of ![]() $M$ with Gram matrix
$M$ with Gram matrix ![]() $\mathrm {Diag}(\mathcal {H}_0,1,\ldots,1,-\nu )$. Choose
$\mathrm {Diag}(\mathcal {H}_0,1,\ldots,1,-\nu )$. Choose ![]() $M(0)= ({t}/2) v_{2k+1}'+ v_{2k+2}'$ with
$M(0)= ({t}/2) v_{2k+1}'+ v_{2k+2}'$ with ![]() $q(M(0))=t$. Then
$q(M(0))=t$. Then
 \begin{align*} M(0)^\perp&=\text{Span}\biggl\{v_1, \ldots, v_{2k}, -\frac{t}2 v_{2k+1}'+ v_{2k+2}', v_{2k+3}', \ldots, v_{2k+m}'\biggr\}\\ & \cong \mathcal{H}^k {\unicode{x29BA}} \text{Span}\{v_{2k+3}', \ldots, v_{2k+m}'\} {\unicode{x29BA}} \langle -t \rangle. \end{align*}
\begin{align*} M(0)^\perp&=\text{Span}\biggl\{v_1, \ldots, v_{2k}, -\frac{t}2 v_{2k+1}'+ v_{2k+2}', v_{2k+3}', \ldots, v_{2k+m}'\biggr\}\\ & \cong \mathcal{H}^k {\unicode{x29BA}} \text{Span}\{v_{2k+3}', \ldots, v_{2k+m}'\} {\unicode{x29BA}} \langle -t \rangle. \end{align*}
as claimed. Moreover,
Next, assume that ![]() $M$ is anisotropic. In this case,
$M$ is anisotropic. In this case, ![]() $M$ has rank
$M$ has rank ![]() $2$ and has Gram matrix
$2$ and has Gram matrix ![]() $\mathrm {Diag}(1, \nu )$ with
$\mathrm {Diag}(1, \nu )$ with ![]() $\chi (M)= \chi (-\nu ) =-1$. In this case,
$\chi (M)= \chi (-\nu ) =-1$. In this case, ![]() $E=F_0(\sqrt {-\nu })$ is a unramified quadratic field extension of
$E=F_0(\sqrt {-\nu })$ is a unramified quadratic field extension of ![]() $F_0$, and
$F_0$, and ![]() $N_{E/F_0}\mathcal {O}_E^\times = \mathcal {O}_{F_0}^\times$. When
$N_{E/F_0}\mathcal {O}_E^\times = \mathcal {O}_{F_0}^\times$. When ![]() $\mathrm {v}(t)=0$,
$\mathrm {v}(t)=0$, ![]() $t \in N_{E/F_0}\mathcal {O}_E^\times$, i.e.
$t \in N_{E/F_0}\mathcal {O}_E^\times$, i.e. ![]() $t =a \bar a + b \bar b \nu$. Take
$t =a \bar a + b \bar b \nu$. Take ![]() $M(0) = a v_{2k+1} + b v_{2k+2}$. Then
$M(0) = a v_{2k+1} + b v_{2k+2}$. Then ![]() $q(M(0))=t$, and
$q(M(0))=t$, and
and
When ![]() $\mathrm {v}(t) >0$,
$\mathrm {v}(t) >0$, ![]() $t \not \in N_{E/F_0}\mathcal {O}_E^\times$. Thus, there is no primitive
$t \not \in N_{E/F_0}\mathcal {O}_E^\times$. Thus, there is no primitive ![]() $M(0) \in M$ with
$M(0) \in M$ with ![]() $q(M(0))=t$. This proves Proposition 5.9(1)–(3).
$q(M(0))=t$. This proves Proposition 5.9(1)–(3).
The proof of part (4) follows from the following four lemmas.
Lemma A.1 For primitive vectors ![]() $w_1,\ w_2\in \mathcal {H}_i$ with
$w_1,\ w_2\in \mathcal {H}_i$ with ![]() $q(w_1)=q(w_2)$, we can find an element
$q(w_1)=q(w_2)$, we can find an element ![]() $g\in \mathrm {U}(\mathcal {H}_i)$ such that
$g\in \mathrm {U}(\mathcal {H}_i)$ such that ![]() $g(w_1)=w_2$.
$g(w_1)=w_2$.
Proof. We treat the case ![]() $i$ is odd first. Assume
$i$ is odd first. Assume ![]() $v=a_1v_1+a_2v_2$. Then
$v=a_1v_1+a_2v_2$. Then ![]() $v$ is primitive implies that
$v$ is primitive implies that ![]() $a_1$ or
$a_1$ or ![]() $a_2$ is a unit. Without loss of generality, we assume
$a_2$ is a unit. Without loss of generality, we assume ![]() $a_2$ is a unit and we can further assume
$a_2$ is a unit and we can further assume ![]() $a_2=1$ by the action of
$a_2=1$ by the action of ![]() $\bigl (\begin {smallmatrix}\bar {a}_2 & 0\\0 & a_2^{-1}\end {smallmatrix}\bigr )$. Now note that
$\bigl (\begin {smallmatrix}\bar {a}_2 & 0\\0 & a_2^{-1}\end {smallmatrix}\bigr )$. Now note that ![]() $q(v)=(v,v)=(a_1-\bar {a}_1)\pi ^{i}$. Hence, we can write
$q(v)=(v,v)=(a_1-\bar {a}_1)\pi ^{i}$. Hence, we can write ![]() $a_1=\alpha +{q(v)\pi ^{-i}}/{2}$, where
$a_1=\alpha +{q(v)\pi ^{-i}}/{2}$, where ![]() $\alpha \in \mathcal {O}_{F_0}$. Now let
$\alpha \in \mathcal {O}_{F_0}$. Now let ![]() $g=\bigl (\begin {smallmatrix}1 & -\alpha \\0 & 1\end {smallmatrix}\bigr )$, and it is straightforward to check that
$g=\bigl (\begin {smallmatrix}1 & -\alpha \\0 & 1\end {smallmatrix}\bigr )$, and it is straightforward to check that ![]() $g\in \mathrm {U}(\mathcal {H}_i)$ and
$g\in \mathrm {U}(\mathcal {H}_i)$ and ![]() $g(v)=({q(v)\pi ^{-i}}/{2})v_1 + v_2$.
$g(v)=({q(v)\pi ^{-i}}/{2})v_1 + v_2$.
Now we deal with the case ![]() $i$ is even. Again, we can assume
$i$ is even. Again, we can assume ![]() $v=a_1v_1+v_2$. Then
$v=a_1v_1+v_2$. Then ![]() $q(v)=(a_1+\bar {a}_1)\pi ^i$. Hence we can write
$q(v)=(a_1+\bar {a}_1)\pi ^i$. Hence we can write ![]() $a_1=({q(v)}/{2})\pi ^{-i}+\beta \pi$, where
$a_1=({q(v)}/{2})\pi ^{-i}+\beta \pi$, where ![]() $\beta \in \mathcal {O}_{F_0}$. Now let
$\beta \in \mathcal {O}_{F_0}$. Now let ![]() $g=\bigl (\begin {smallmatrix}1 & -\beta \pi \\0 & 1\end {smallmatrix}\bigr )$, and it is straightforward to check that
$g=\bigl (\begin {smallmatrix}1 & -\beta \pi \\0 & 1\end {smallmatrix}\bigr )$, and it is straightforward to check that ![]() $g\in \mathrm {U}(\mathcal {H}_i)$ and
$g\in \mathrm {U}(\mathcal {H}_i)$ and ![]() $g(v)=({q(v)\pi ^{-i}}/{2})v_1+v_2$.
$g(v)=({q(v)\pi ^{-i}}/{2})v_1+v_2$.
Lemma A.2 Assume ![]() $M$ is any lattice such that
$M$ is any lattice such that ![]() $\mathrm {v}(M)\geq i$. For
$\mathrm {v}(M)\geq i$. For ![]() $w_1,\ w_2 \in \mathcal {H}_i^k{\unicode{x29BA}} M$, if
$w_1,\ w_2 \in \mathcal {H}_i^k{\unicode{x29BA}} M$, if ![]() $\Pr _{\mathcal {H}_{i}^k}(w_1)$ and
$\Pr _{\mathcal {H}_{i}^k}(w_1)$ and ![]() $\Pr _{\mathcal {H}_{i}^k}(w_2)$ are primitive and
$\Pr _{\mathcal {H}_{i}^k}(w_2)$ are primitive and ![]() $q(w_1)=q(w_2)$, then there exists
$q(w_1)=q(w_2)$, then there exists ![]() $g\in \mathrm {U}(\mathcal {H}_i^k{\unicode{x29BA}} M)$ with
$g\in \mathrm {U}(\mathcal {H}_i^k{\unicode{x29BA}} M)$ with ![]() $g(w_1)=w_2$.
$g(w_1)=w_2$.
Proof. Choose a basis ![]() $\{v_1,\ldots,v_{2k}\}$ of
$\{v_1,\ldots,v_{2k}\}$ of ![]() $\mathcal {H}_i^{k}$ such that the associated Gram matrix is
$\mathcal {H}_i^{k}$ such that the associated Gram matrix is ![]() $\mathcal {H}_i^k$. We also choose a basis
$\mathcal {H}_i^k$. We also choose a basis ![]() $\{v_{2k+1},\ldots,v_{2k+m}\}$ of
$\{v_{2k+1},\ldots,v_{2k+m}\}$ of ![]() $M$. Write
$M$. Write ![]() $w_1=\sum _{i=1}^{2k+m}a_iv_i$. Since
$w_1=\sum _{i=1}^{2k+m}a_iv_i$. Since ![]() $\mathrm {Pr}_{\mathcal {H}_i^k}(w_1)$ is primitive,
$\mathrm {Pr}_{\mathcal {H}_i^k}(w_1)$ is primitive, ![]() $a_i$ is a unit for some
$a_i$ is a unit for some ![]() $i\in \{1,\ldots,2k\}$. Without loss of generality, we may assume
$i\in \{1,\ldots,2k\}$. Without loss of generality, we may assume ![]() $a_1=1$. Let
$a_1=1$. Let ![]() $w'=w_1+({(-1)^{i+1}q(w_1)\pi ^{-i}}/{2}) v_2$, then
$w'=w_1+({(-1)^{i+1}q(w_1)\pi ^{-i}}/{2}) v_2$, then
and ![]() $(w', v_2) =(v_1, v_2)$. As a result,
$(w', v_2) =(v_1, v_2)$. As a result, ![]() $M_1=\mathrm {Span}_{\mathcal {O}_F}\{w_1,v_2\}=\mathrm {Span}_{\mathcal {O}_F}\{w',v_2\}$ is isometric to
$M_1=\mathrm {Span}_{\mathcal {O}_F}\{w_1,v_2\}=\mathrm {Span}_{\mathcal {O}_F}\{w',v_2\}$ is isometric to ![]() $\mathcal {H}_i$. Note that
$\mathcal {H}_i$. Note that ![]() $\mathrm {val}_{\pi }(q(w_1))\ge i$ is guaranteed by the assumption
$\mathrm {val}_{\pi }(q(w_1))\ge i$ is guaranteed by the assumption ![]() $\mathrm {v}(M)\ge i$.
$\mathrm {v}(M)\ge i$.
Similarly, we can show ![]() $w_2\in M_2$ for some
$w_2\in M_2$ for some ![]() $M_2$ that is isometric to
$M_2$ that is isometric to ![]() $\mathcal {H}_i$. However, the assumption
$\mathcal {H}_i$. However, the assumption ![]() $\mathrm {v}(M)\ge i$ and [Reference JacobowitzJac62, Proposition
$\mathrm {v}(M)\ge i$ and [Reference JacobowitzJac62, Proposition ![]() $4.2$] imply that there exist
$4.2$] imply that there exist ![]() $g\in \mathrm {U}(\mathcal {H}_i^k{\unicode{x29BA}} M)$ such that
$g\in \mathrm {U}(\mathcal {H}_i^k{\unicode{x29BA}} M)$ such that ![]() $g(M_1)=M_2$. In particular,
$g(M_1)=M_2$. In particular, ![]() $g(w_1)\in M_2$. Since both
$g(w_1)\in M_2$. Since both ![]() $g(w_1)$ and
$g(w_1)$ and ![]() $w_2$ are in
$w_2$ are in ![]() $M_2$, the problem is reduced to Lemma A.1.
$M_2$, the problem is reduced to Lemma A.1.
Lemma A.3 For primitive vectors ![]() $w_1,\ w_2\in M$ with
$w_1,\ w_2\in M$ with ![]() $q(w_1)=q(w_2)$, we can find an element
$q(w_1)=q(w_2)$, we can find an element ![]() $g\in \mathrm {U}(M)$ such that
$g\in \mathrm {U}(M)$ such that ![]() $g(w_1)=w_2.$
$g(w_1)=w_2.$
Proof. Since ![]() $M$ is unimodular, we can decompose
$M$ is unimodular, we can decompose
where ![]() $M'=0$ or an anisotropic unimodular Hermiatian lattice of rank
$M'=0$ or an anisotropic unimodular Hermiatian lattice of rank ![]() $1$ or
$1$ or ![]() $2$. If
$2$. If ![]() $\Pr _{\mathcal {H}_{0}^k}(w_1)$ and
$\Pr _{\mathcal {H}_{0}^k}(w_1)$ and ![]() $\Pr _{\mathcal {H}_{0}^k}(w_2)$ are primitive, this is Lemma A.2. If
$\Pr _{\mathcal {H}_{0}^k}(w_2)$ are primitive, this is Lemma A.2. If ![]() $\Pr _{\mathcal {H}_{0}^k}(w_1)$ is not primitive, then
$\Pr _{\mathcal {H}_{0}^k}(w_1)$ is not primitive, then ![]() $\Pr _{M'}(w_1)$ is primitive and, thus,
$\Pr _{M'}(w_1)$ is primitive and, thus, ![]() $q(\Pr _{M'}(w_1)) \in \mathcal {O}_F^\times$. This implies that
$q(\Pr _{M'}(w_1)) \in \mathcal {O}_F^\times$. This implies that ![]() $q(w_2)=q(w_1)$ is a unit, and
$q(w_2)=q(w_1)$ is a unit, and ![]() $M= \mathcal {O}_F w_i {\unicode{x29BA}} (\mathcal {O}_F w_i)^\perp$. Therefore, there is some
$M= \mathcal {O}_F w_i {\unicode{x29BA}} (\mathcal {O}_F w_i)^\perp$. Therefore, there is some ![]() $g \in \mathrm {U}(M)$ with
$g \in \mathrm {U}(M)$ with ![]() $g(w_1)=w_2$.
$g(w_1)=w_2$.
Lemma A.4 Assume that ![]() $w_1,\ w_2\in M^{[k]}$ are primitive and that
$w_1,\ w_2\in M^{[k]}$ are primitive and that ![]() $\Pr _{\mathcal {H}^k}(w_1)$ and
$\Pr _{\mathcal {H}^k}(w_1)$ and ![]() $\Pr _{\mathcal {H}^k}(w_2)$ are not primitive. Then we can find
$\Pr _{\mathcal {H}^k}(w_2)$ are not primitive. Then we can find ![]() $g\in \mathrm {U}(M^{[k]})$ such that
$g\in \mathrm {U}(M^{[k]})$ such that ![]() $g(w_1)=w_2$.
$g(w_1)=w_2$.
Proof. Let ![]() $\{v_1,\ldots,v_{2k+m}\}$ be a basis of
$\{v_1,\ldots,v_{2k+m}\}$ be a basis of ![]() $\mathcal {H}^k{\unicode{x29BA}} M$, whose Gram matrix is
$\mathcal {H}^k{\unicode{x29BA}} M$, whose Gram matrix is ![]() $\mathcal {H}^k{\unicode{x29BA}} \mathrm {Diag}(1,\ldots,\nu )$ where
$\mathcal {H}^k{\unicode{x29BA}} \mathrm {Diag}(1,\ldots,\nu )$ where ![]() $\nu$ is a unit. Assume
$\nu$ is a unit. Assume ![]() $v\in M^{[k]}$ is primitive and
$v\in M^{[k]}$ is primitive and ![]() $\Pr _{\mathcal {H}^k}(v)$ is not primitive, then we can write
$\Pr _{\mathcal {H}^k}(v)$ is not primitive, then we can write ![]() $v=\sum _{i=1}^{2k}\pi a_i v_i + \sum _{j=2k+1}^{2k+m}a_jv_j$, where some
$v=\sum _{i=1}^{2k}\pi a_i v_i + \sum _{j=2k+1}^{2k+m}a_jv_j$, where some ![]() $a_j$ is a unit for
$a_j$ is a unit for ![]() $2k+1\leq j \leq 2k+m.$ Again, without loss of generality, we may assume
$2k+1\leq j \leq 2k+m.$ Again, without loss of generality, we may assume ![]() $a_{2k+m}=1.$ For
$a_{2k+m}=1.$ For ![]() $i\leq k$, we set
$i\leq k$, we set
Let ![]() $M_v=\mathrm {Span}_{\mathcal {O}_F}\{v_1',\ldots,v_{2k}'\}.$ Then it is easy to check that
$M_v=\mathrm {Span}_{\mathcal {O}_F}\{v_1',\ldots,v_{2k}'\}.$ Then it is easy to check that ![]() $M_v$ is perpendicular to
$M_v$ is perpendicular to ![]() $v$. Moreover,
$v$. Moreover, ![]() $M_v$ is isometric to
$M_v$ is isometric to ![]() $\mathcal {H}^{k}$ since
$\mathcal {H}^{k}$ since ![]() $\mathrm {val}_{\pi }((v'_{2i-1},v'_{2i}))=-1$ and
$\mathrm {val}_{\pi }((v'_{2i-1},v'_{2i}))=-1$ and ![]() $0\leq \mathrm {val}_{\pi }((v'_i,v'_j))$ for other
$0\leq \mathrm {val}_{\pi }((v'_i,v'_j))$ for other ![]() $1\leq i,j\leq 2k$. Hence, we can find
$1\leq i,j\leq 2k$. Hence, we can find ![]() $g_v\in \mathrm {U}(M^{[k]})$ such that
$g_v\in \mathrm {U}(M^{[k]})$ such that ![]() $g_v(M_v)=\mathrm {Span_{\mathcal {O}_F}}\{v_1,\ldots,v_{2k}\}$ and
$g_v(M_v)=\mathrm {Span_{\mathcal {O}_F}}\{v_1,\ldots,v_{2k}\}$ and ![]() $g_v(v)\in \mathrm {Span_{\mathcal {O}_F}}\{v_{2k+1},\ldots,v_{2k+m}\}=M$.
$g_v(v)\in \mathrm {Span_{\mathcal {O}_F}}\{v_{2k+1},\ldots,v_{2k+m}\}=M$.
Applying the above to ![]() $w_1$ and
$w_1$ and ![]() $w_2$, we can find
$w_2$, we can find ![]() $g_{w_1},g_{w_2}\in \mathrm {U}(M^{[k]})$ such that
$g_{w_1},g_{w_2}\in \mathrm {U}(M^{[k]})$ such that ![]() $g_{w_1}(w_1),\ g_{w_2}(w_2)\in M$. Now the problem is reduced to Lemma A.3, and the lemma is proved.
$g_{w_1}(w_1),\ g_{w_2}(w_2)\in M$. Now the problem is reduced to Lemma A.3, and the lemma is proved.
According to Lemmas A.2 and A.4, a primitive vector ![]() $v\in M^{[k]}$ is either in the same orbit of a vector
$v\in M^{[k]}$ is either in the same orbit of a vector ![]() $M(1)\in \mathcal {H}^k$ or a vector
$M(1)\in \mathcal {H}^k$ or a vector ![]() $M(0)\in M$. Lemma A.1 implies that primitive vectors
$M(0)\in M$. Lemma A.1 implies that primitive vectors ![]() $M(1),M'(1)\in \mathcal {H}^k$ with
$M(1),M'(1)\in \mathcal {H}^k$ with ![]() $q(M(1))=q(M'(1))$ lie in the same orbit. Lemma A.3 implies the similar result for primitive
$q(M(1))=q(M'(1))$ lie in the same orbit. Lemma A.3 implies the similar result for primitive ![]() $M(0),M'(0)\in M$ with
$M(0),M'(0)\in M$ with ![]() $q(M(0))=q(M'(0))$. A combination of the above proves part
$q(M(0))=q(M'(0))$. A combination of the above proves part ![]() $(4)$ of Proposition 5.9.
$(4)$ of Proposition 5.9.
A.2 Proof of Proposition 5.10
In this subsection, we prove the first part of Proposition 5.10, which we restate as follows for the convenience of the reader.
Proposition A.5 Let ![]() $L$ be a Hermitian
$L$ be a Hermitian ![]() $\mathcal {O}_F$-lattice of rank
$\mathcal {O}_F$-lattice of rank ![]() $2$ and
$2$ and ![]() $\mathrm {v}(L) >0$. Let
$\mathrm {v}(L) >0$. Let ![]() $\varphi :L\rightarrow M^{[k]}$ be a primitive isometric embedding. Let
$\varphi :L\rightarrow M^{[k]}$ be a primitive isometric embedding. Let ![]() $d(\varphi )$ be the dimension of the image of the map
$d(\varphi )$ be the dimension of the image of the map
in ![]() $\mathcal {H}^k/\pi \mathcal {H}^k$. Then
$\mathcal {H}^k/\pi \mathcal {H}^k$. Then
where ![]() $M^{(d(\varphi ))}$ is unimodular of rank equal to
$M^{(d(\varphi ))}$ is unimodular of rank equal to ![]() $(\mathrm {rank}(M)-2(2-d(\varphi )))$ and
$(\mathrm {rank}(M)-2(2-d(\varphi )))$ and ![]() $\mathrm {det} M^{(d(\varphi ))}=(-1)^{d(\varphi )}\mathrm {det} M$. In particular, if
$\mathrm {det} M^{(d(\varphi ))}=(-1)^{d(\varphi )}\mathrm {det} M$. In particular, if ![]() $d(\varphi )=1$, then
$d(\varphi )=1$, then ![]() $\mathrm {rank}(M)\geq 2$, and if
$\mathrm {rank}(M)\geq 2$, and if ![]() $d(\varphi )=0$, then
$d(\varphi )=0$, then ![]() $\mathrm {rank}(M)\geq 4$.
$\mathrm {rank}(M)\geq 4$.
Lemma A.6 Let the notation be as in Proposition A.5. If ![]() $\mathrm {rank}(M^{[k]})\le 4$, then
$\mathrm {rank}(M^{[k]})\le 4$, then
In particular, such an ![]() $\varphi$ does not exist if
$\varphi$ does not exist if ![]() $\chi (M^{[k]})=-1$ or
$\chi (M^{[k]})=-1$ or ![]() $\mathrm {rank}(M^{[k]}) <4$.
$\mathrm {rank}(M^{[k]}) <4$.
Proof. First, assume ![]() $M^{[k]}=\mathcal {H}^2$ and
$M^{[k]}=\mathcal {H}^2$ and ![]() $L\approx \mathcal {H}_i$ where
$L\approx \mathcal {H}_i$ where ![]() $i>0$. Let
$i>0$. Let ![]() $\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of
$\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of ![]() $\{w_1,w_2\}$ is
$\{w_1,w_2\}$ is ![]() $\mathcal {H}_i$. By Lemma A.1, we may assume
$\mathcal {H}_i$. By Lemma A.1, we may assume ![]() $w_1=v_1$. Then we may write
$w_1=v_1$. Then we may write ![]() $w_2=a_1v_1+\pi ^{i+1}v_2+a_3v_3+a_4v_4,$ and
$w_2=a_1v_1+\pi ^{i+1}v_2+a_3v_3+a_4v_4,$ and ![]() $\min \{\mathrm {v}_{\pi }(a_3),\mathrm {v}_{\pi }(a_4)\}=0$ by assumption. Without loss of generality, we may assume
$\min \{\mathrm {v}_{\pi }(a_3),\mathrm {v}_{\pi }(a_4)\}=0$ by assumption. Without loss of generality, we may assume ![]() $a_3=1$. Now a direct calculation shows that
$a_3=1$. Now a direct calculation shows that
Its Gram matrix is
hence
Now we treat the case ![]() $M^{[k]}=\mathcal {H}^2$ and
$M^{[k]}=\mathcal {H}^2$ and ![]() $L\approx \mathrm {Diag}(u_1(-\pi _0^a),u_2(-\pi _0)^b)$ where
$L\approx \mathrm {Diag}(u_1(-\pi _0^a),u_2(-\pi _0)^b)$ where ![]() $0< a\le b$. Again, let
$0< a\le b$. Again, let ![]() $\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of
$\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of ![]() $\{w_1,w_2\}$ is
$\{w_1,w_2\}$ is ![]() $\mathrm {Diag}(u_1(-\pi _0^a),u_2(-\pi _0)^b)$, and we can assume
$\mathrm {Diag}(u_1(-\pi _0^a),u_2(-\pi _0)^b)$, and we can assume ![]() $w_1=v_1-({q(w_1)\pi }/{2})v_2$ without loss of generality. Then we may write
$w_1=v_1-({q(w_1)\pi }/{2})v_2$ without loss of generality. Then we may write ![]() $w_2=a_1(v_1+({q(w_1)\pi }/{2})v_2)+a_3v_3+a_4v_4$, hence
$w_2=a_1(v_1+({q(w_1)\pi }/{2})v_2)+a_3v_3+a_4v_4$, hence ![]() $\min \{v_{\pi }(a_3),v_{\pi }(a_4)\}=0$ by assumption again. We may assume
$\min \{v_{\pi }(a_3),v_{\pi }(a_4)\}=0$ by assumption again. We may assume ![]() $a_3=1$ and a direct calculation shows that
$a_3=1$ and a direct calculation shows that
Set
Then ![]() $\varphi (L)^\perp =\mathrm {Span_{\mathcal {O}_F}}\{v_3',v_4'\}$ and the Gram matrix of
$\varphi (L)^\perp =\mathrm {Span_{\mathcal {O}_F}}\{v_3',v_4'\}$ and the Gram matrix of ![]() $\{v_3',v_4'\}$ is
$\{v_3',v_4'\}$ is
Now assume ![]() $M^{[k]}=\mathcal {H}{\unicode{x29BA}} M$, where
$M^{[k]}=\mathcal {H}{\unicode{x29BA}} M$, where ![]() $M$ is unimodular of rank
$M$ is unimodular of rank ![]() $2$. We only treat the case
$2$. We only treat the case ![]() $L\approx \mathcal {H}_i$ in detail, and the argument for
$L\approx \mathcal {H}_i$ in detail, and the argument for ![]() $L$ represented by a diagonal matrix is similar. We assume that
$L$ represented by a diagonal matrix is similar. We assume that ![]() $M^{[k]}$ has a basis
$M^{[k]}$ has a basis ![]() $\{v_1,\ldots,v_4\}$ with Gram matrix
$\{v_1,\ldots,v_4\}$ with Gram matrix ![]() $\mathcal {H}{\unicode{x29BA}} \mathrm {Diag}(1,\nu )$ where
$\mathcal {H}{\unicode{x29BA}} \mathrm {Diag}(1,\nu )$ where ![]() $\nu$ is a unit. Let
$\nu$ is a unit. Let ![]() $\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ where the Gram matrix of
$\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ where the Gram matrix of ![]() $\{w_1,w_2\}$ is
$\{w_1,w_2\}$ is ![]() $\mathcal {H}_i$. Then one can check that at least one of
$\mathcal {H}_i$. Then one can check that at least one of ![]() $w_1$ and
$w_1$ and ![]() $w_2$ is primitive in
$w_2$ is primitive in ![]() $\mathcal {H}$. By Lemma A.1, we can assume that
$\mathcal {H}$. By Lemma A.1, we can assume that
and
By our assumption we know that ![]() $\min \{\mathrm {v}_\pi (a_3),\mathrm {v}_\pi (a_4)\}=0$. Since we assume
$\min \{\mathrm {v}_\pi (a_3),\mathrm {v}_\pi (a_4)\}=0$. Since we assume ![]() $i\geq 1$, (A.2) implies that both
$i\geq 1$, (A.2) implies that both ![]() $a_3$ and
$a_3$ and ![]() $a_4$ are in
$a_4$ are in ![]() $\mathcal {O}_{F_0}^\times$. This, in turn, implies that
$\mathcal {O}_{F_0}^\times$. This, in turn, implies that ![]() $-\nu \in \mathrm {Nm}_{F/F_0^\times }(\mathcal {O}_F^\times )=\mathcal {O}_{F_0}^2$. Hence,
$-\nu \in \mathrm {Nm}_{F/F_0^\times }(\mathcal {O}_F^\times )=\mathcal {O}_{F_0}^2$. Hence, ![]() $M^{[k]}\approx \mathcal {H}{\unicode{x29BA}} \mathcal {H}_0$ and we can instead assume that
$M^{[k]}\approx \mathcal {H}{\unicode{x29BA}} \mathcal {H}_0$ and we can instead assume that ![]() $\{v_1,v_2,v_3,v_4\}$ has Gram matrix
$\{v_1,v_2,v_3,v_4\}$ has Gram matrix ![]() $\mathcal {H}{\unicode{x29BA}} \mathcal {H}_0$. We can further assume that
$\mathcal {H}{\unicode{x29BA}} \mathcal {H}_0$. We can further assume that
with
By direct calculation, it is easy to see that
Its Gram matrix is
Finally, assume ![]() $M^{[k]}$ is unimodular of rank
$M^{[k]}$ is unimodular of rank ![]() $4$. We treat the case
$4$. We treat the case ![]() $L\approx \mathcal {H}_i$ in detail, and the other cases follow from a similar argument. Let
$L\approx \mathcal {H}_i$ in detail, and the other cases follow from a similar argument. Let ![]() $\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of
$\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$ such that the Gram matrix of ![]() $\{w_1,w_2\}$ is
$\{w_1,w_2\}$ is ![]() $\mathcal {H}_i$. Apparently
$\mathcal {H}_i$. Apparently ![]() $M^{[k]}$ contains a
$M^{[k]}$ contains a ![]() $\mathcal {H}_0$. We can assume that
$\mathcal {H}_0$. We can assume that ![]() $M^{[k]}$ has a basis
$M^{[k]}$ has a basis ![]() $\{v_1,v_2,v_3,v_4\}$ with Gram matrix
$\{v_1,v_2,v_3,v_4\}$ with Gram matrix ![]() $\mathcal {H}_0{\unicode{x29BA}} \mathrm {diag}\{1,\epsilon \}$ where
$\mathcal {H}_0{\unicode{x29BA}} \mathrm {diag}\{1,\epsilon \}$ where ![]() $\epsilon \in \mathcal {O}_{F_0}^\times$. By Lemma A.3 we can assume that
$\epsilon \in \mathcal {O}_{F_0}^\times$. By Lemma A.3 we can assume that ![]() $w_1=v_1$. Then we have
$w_1=v_1$. Then we have
 \[ w_2=a_1 v_1+\pi^{i} v_2+\sum_{j=3}^4 a_j v_j, \]
\[ w_2=a_1 v_1+\pi^{i} v_2+\sum_{j=3}^4 a_j v_j, \]
and
By our assumption we know that ![]() $\min \{\mathrm {v}_\pi (a_3),\mathrm {v}_\pi (a_4)\}=0$. Since we assume
$\min \{\mathrm {v}_\pi (a_3),\mathrm {v}_\pi (a_4)\}=0$. Since we assume ![]() $i\geq 1$, (A.3) implies that both
$i\geq 1$, (A.3) implies that both ![]() $a_3$ and
$a_3$ and ![]() $a_4$ are in
$a_4$ are in ![]() $\mathcal {O}_{F_0}^\times$. This, in turn, implies that
$\mathcal {O}_{F_0}^\times$. This, in turn, implies that ![]() $-\epsilon \in \mathrm {Nm}_{F/F_0^\times }(\mathcal {O}_F^\times )=\mathcal {O}_{F_0}^2$. Hence,
$-\epsilon \in \mathrm {Nm}_{F/F_0^\times }(\mathcal {O}_F^\times )=\mathcal {O}_{F_0}^2$. Hence, ![]() $M^{[k]}=\mathcal {H}_0^2$ and we can instead assume that
$M^{[k]}=\mathcal {H}_0^2$ and we can instead assume that ![]() $\{v_1,v_2,v_3,v_4\}$ has Gram matrix
$\{v_1,v_2,v_3,v_4\}$ has Gram matrix ![]() $\mathcal {H}_0{\unicode{x29BA}} \mathcal {H}_0$. We can further assume that
$\mathcal {H}_0{\unicode{x29BA}} \mathcal {H}_0$. We can further assume that
with
By a direct calculation, it is easy to see that
Its Gram matrix is
Note that, as a byproduct of the above argument, we actually also proved that if ![]() $\mathrm {rank}(M^{[k]})<4$ or
$\mathrm {rank}(M^{[k]})<4$ or ![]() $M$ is not split, then no such
$M$ is not split, then no such ![]() $\varphi$ exists. The lemma is proved.
$\varphi$ exists. The lemma is proved.
Lemma A.7 Assume ![]() $\mathrm {v}(L)\ge 0$. Let
$\mathrm {v}(L)\ge 0$. Let ![]() $\varphi :L\rightarrow M^{[k]}$ be a primitive isometric embedding. Let
$\varphi :L\rightarrow M^{[k]}$ be a primitive isometric embedding. Let ![]() $d(\varphi )$ be the dimension of
$d(\varphi )$ be the dimension of ![]() $\mathrm {Pr}_{\mathcal {H}^k}(\varphi (L))\otimes _{\mathcal {O}_F}\mathbb {F}_{q}$ in
$\mathrm {Pr}_{\mathcal {H}^k}(\varphi (L))\otimes _{\mathcal {O}_F}\mathbb {F}_{q}$ in ![]() $\mathcal {H}^k/\pi \mathcal {H}^k$. Then there exist a
$\mathcal {H}^k/\pi \mathcal {H}^k$. Then there exist a ![]() $g\in \mathrm {U}(M^{[k]})$ such that
$g\in \mathrm {U}(M^{[k]})$ such that
where ![]() $I_{4-2d(\varphi )}$ is a unimodular sublattice of
$I_{4-2d(\varphi )}$ is a unimodular sublattice of ![]() $M^{[k]}$ with rank
$M^{[k]}$ with rank ![]() $4-2d(\varphi )$.
$4-2d(\varphi )$.
Proof. We prove the case for ![]() $L\approx \mathcal {H}_i$ in detail, and the other cases are similar. Let
$L\approx \mathcal {H}_i$ in detail, and the other cases are similar. Let ![]() $\{v_1,\ldots,v_{2k+m}\}$ be a basis of
$\{v_1,\ldots,v_{2k+m}\}$ be a basis of ![]() $M^{[k]}$ whose Gram matrix is
$M^{[k]}$ whose Gram matrix is ![]() $\mathcal {H}^k{\unicode{x29BA}} \mathrm {diag}\{1,\ldots,1,\nu \}$ where
$\mathcal {H}^k{\unicode{x29BA}} \mathrm {diag}\{1,\ldots,1,\nu \}$ where ![]() $\nu$ is a unit. Set
$\nu$ is a unit. Set ![]() $\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$.
$\varphi (L)=\mathrm {Span_{\mathcal {O}_F}}\{w_1,w_2\}$.
Assume ![]() $d(\varphi )=2$. If
$d(\varphi )=2$. If ![]() $i=-1$, then there is nothing to prove. Therefore, we may assume
$i=-1$, then there is nothing to prove. Therefore, we may assume ![]() $i>-1$. By Lemma A.2, without loss of generality, we can assume that
$i>-1$. By Lemma A.2, without loss of generality, we can assume that ![]() $w_1=v_1$. Then
$w_1=v_1$. Then
 \[ w_2=a_1v_1+\pi^{i+1} v_2+\sum_{j=3}^{2k+m} a_j v_j. \]
\[ w_2=a_1v_1+\pi^{i+1} v_2+\sum_{j=3}^{2k+m} a_j v_j. \]
By the assumption that ![]() $d(\varphi )=2$, we know that
$d(\varphi )=2$, we know that
Hence, applying Lemma A.2 to ![]() $\mathcal {H}^{k-1}{\unicode{x29BA}} M$, we can find a
$\mathcal {H}^{k-1}{\unicode{x29BA}} M$, we can find a ![]() $g\in \mathrm {U}(M^{[k]})$ such that
$g\in \mathrm {U}(M^{[k]})$ such that
where ![]() $\mathcal {H}^2$ refers to the first direct summand in the decomposition
$\mathcal {H}^2$ refers to the first direct summand in the decomposition ![]() $\mathcal {H}^k{\unicode{x29BA}} M=\mathcal {H}^2{\unicode{x29BA}} \mathcal {H}^{k-2}{\unicode{x29BA}} M$.
$\mathcal {H}^k{\unicode{x29BA}} M=\mathcal {H}^2{\unicode{x29BA}} \mathcal {H}^{k-2}{\unicode{x29BA}} M$.
When ![]() $d(\varphi )=1$, without loss of generality, we can assume
$d(\varphi )=1$, without loss of generality, we can assume ![]() $\Pr _{\mathcal {H}^k}(w_1)$ is primitive. By Lemma A.2, we can assume that
$\Pr _{\mathcal {H}^k}(w_1)$ is primitive. By Lemma A.2, we can assume that ![]() $w_1=v_1$. Then
$w_1=v_1$. Then
 \[ w_2=a_1v_1+\pi^{i+1} v_2+\sum_{j=3}^{2k+m} a_j v_j. \]
\[ w_2=a_1v_1+\pi^{i+1} v_2+\sum_{j=3}^{2k+m} a_j v_j. \]
By the assumption that ![]() $d(\varphi )=1$, we know that
$d(\varphi )=1$, we know that
Since we assume ![]() $\varphi$ is primitive, we know that
$\varphi$ is primitive, we know that
Then we are done by applying Lemma A.4 to ![]() $\mathcal {H}^{k-1} {\unicode{x29BA}} M$.
$\mathcal {H}^{k-1} {\unicode{x29BA}} M$.
When ![]() $d(\varphi )=0$, without loss of generality, we may assume
$d(\varphi )=0$, without loss of generality, we may assume ![]() $w_1=v_{2k+1}+v_{2k+2}$ by Lemma A.4. Here, we pick
$w_1=v_{2k+1}+v_{2k+2}$ by Lemma A.4. Here, we pick ![]() $v_{2k+i}$ so that the corresponding Gram matrix is
$v_{2k+i}$ so that the corresponding Gram matrix is ![]() $\mathrm {Diag}(1,-1,1,\ldots,-\nu )$ (this is possible since we assume
$\mathrm {Diag}(1,-1,1,\ldots,-\nu )$ (this is possible since we assume ![]() $m\ge 4$). Since
$m\ge 4$). Since ![]() $\varphi$ is primitive with
$\varphi$ is primitive with ![]() $d(\varphi )=0$, then
$d(\varphi )=0$, then
 \[ w_2=\sum_{i=1}^{2k}\pi a_iv_i+\sum_{i=2k+1}^{2k+m}a_iv_i, \]
\[ w_2=\sum_{i=1}^{2k}\pi a_iv_i+\sum_{i=2k+1}^{2k+m}a_iv_i, \]
and
We are done by applying Lemma A.4 to ![]() $\mathcal {H}^k{\unicode{x29BA}} \mathrm {Span_{\mathcal {O}_F}}\{v_{2k+3},\ldots,v_{2k+m}\}$.
$\mathcal {H}^k{\unicode{x29BA}} \mathrm {Span_{\mathcal {O}_F}}\{v_{2k+3},\ldots,v_{2k+m}\}$.
A.3 Calculation of primitive local density
In this subsection, we compute primitive local density polynomials and prove the formulas in Propositions 5.9 and 5.10. Assume ![]() $L$ is represented by a non-singular Hermitian matrix
$L$ is represented by a non-singular Hermitian matrix ![]() $T$ of rank
$T$ of rank ![]() $n\le 2$. We let
$n\le 2$. We let ![]() $\bar {v}$ denote the image of
$\bar {v}$ denote the image of ![]() $v$ in
$v$ in ![]() $M^{[k]}\otimes _{\mathcal {O}_F}\mathbb {F}_q$. Let
$M^{[k]}\otimes _{\mathcal {O}_F}\mathbb {F}_q$. Let
where ![]() $M^{n,(n)}$ is as in (5.5), and
$M^{n,(n)}$ is as in (5.5), and
Note that
 \begin{equation} \sum_{i=0}^{n}\beta_i(M, L,X)=\beta(M, L,X)^{(n)} \end{equation}
\begin{equation} \sum_{i=0}^{n}\beta_i(M, L,X)=\beta(M, L,X)^{(n)} \end{equation}
is the primitive local density defined earlier, and we will shorten it as ![]() $\beta (M, L,X)$. Note that if
$\beta (M, L,X)$. Note that if ![]() $L$ is of the form
$L$ is of the form ![]() $\mathcal {H}^{j}$, then
$\mathcal {H}^{j}$, then ![]() $\beta (M, L,X)=\beta _{n}(M, L,X)$.
$\beta (M, L,X)=\beta _{n}(M, L,X)$.
First, by a variant of [Reference Cho and YamauchiCY20], Chao Li and Yifeng Liu obtained the following formula of ![]() $\beta (\mathcal {H}^k,L)$.
$\beta (\mathcal {H}^k,L)$.
Lemma A.8 [Reference Li and LiuLL22, Lemma ![]() $2.16$]
$2.16$]
Let ![]() $b_1\le \cdots \le b_n$ be the unique integers such that
$b_1\le \cdots \le b_n$ be the unique integers such that ![]() $L^{\vee }/L\approx \mathcal {O}_F/(\pi ^{b_1})\oplus \cdots \oplus \mathcal {O}_F/(\pi ^{b_n})$. Let
$L^{\vee }/L\approx \mathcal {O}_F/(\pi ^{b_1})\oplus \cdots \oplus \mathcal {O}_F/(\pi ^{b_n})$. Let ![]() $t_o(L)$ be the number of non-zero entries in
$t_o(L)$ be the number of non-zero entries in ![]() $(b_1,\ldots,b_n)$. Then
$(b_1,\ldots,b_n)$. Then
Lemma A.9 Assume ![]() $L$ is of rank
$L$ is of rank ![]() $n$, then
$n$, then
In particular, if ![]() $L$ is of the form
$L$ is of the form ![]() $\mathcal {H}^j$, then
$\mathcal {H}^j$, then
Proof. Recall that ![]() $T({\bf x})=({\bf x}, {\bf x})$ is the moment matrix of
$T({\bf x})=({\bf x}, {\bf x})$ is the moment matrix of ![]() ${\bf x} \in (M^{[k]})^n$. For a
${\bf x} \in (M^{[k]})^n$. For a ![]() ${\bf x}_2 \in M^n$, let
${\bf x}_2 \in M^n$, let ![]() $T'({\bf x}_2)=T-T({\bf x}_2)$. Then
$T'({\bf x}_2)=T-T({\bf x}_2)$. Then
 \begin{align*} \beta_n( M,L,q^{-2k}) &=\int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}}\psi (\langle Y,T({}^t({\bf x}_1,{\bf x}_2))-T \rangle)\,d{\bf x}_{1} \,d{\bf x}_{2}\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)+T({\bf x}_2)-T\rangle)\,d{\bf x}_1 \,d{\bf x}_2\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T'({\bf x}_2)\rangle)\,d{\bf x}_1 \,d{\bf x}_2. \end{align*}
\begin{align*} \beta_n( M,L,q^{-2k}) &=\int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}}\psi (\langle Y,T({}^t({\bf x}_1,{\bf x}_2))-T \rangle)\,d{\bf x}_{1} \,d{\bf x}_{2}\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)+T({\bf x}_2)-T\rangle)\,d{\bf x}_1 \,d{\bf x}_2\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{M^n} \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T'({\bf x}_2)\rangle)\,d{\bf x}_1 \,d{\bf x}_2. \end{align*}
Note that if ![]() $L$ and
$L$ and ![]() $L'$ are two Hermitian
$L'$ are two Hermitian ![]() $\mathcal {O}_F$-lattices with moment matrix
$\mathcal {O}_F$-lattices with moment matrix ![]() $T$ and
$T$ and ![]() $T'$ such that
$T'$ such that ![]() $T-T'\in \mathrm {Herm}_n(\mathcal {O}_{F_0})$, then
$T-T'\in \mathrm {Herm}_n(\mathcal {O}_{F_0})$, then ![]() $t_o(L)=t_o(L')$. Hence, for any
$t_o(L)=t_o(L')$. Hence, for any ![]() ${\bf x}_2 \in M^n$, we have by Lemma A.8
${\bf x}_2 \in M^n$, we have by Lemma A.8
 \begin{align*} \beta(\mathcal{H}^k,T'({\bf x}_2))&= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T'({\bf x}_2)\rangle)\,d{\bf x}_1 \\ &=\int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &=\beta(\mathcal{H}^k,T). \end{align*}
\begin{align*} \beta(\mathcal{H}^k,T'({\bf x}_2))&= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T'({\bf x}_2)\rangle)\,d{\bf x}_1 \\ &=\int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &=\beta(\mathcal{H}^k,T). \end{align*}
Therefore,
 \begin{align*} \beta_n(M,L,q^{-2k}) &=\mathrm{vol}(M^n,d{\bf x}_2) \cdot \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &= \beta(\mathcal{H}^k,L). \end{align*}
\begin{align*} \beta_n(M,L,q^{-2k}) &=\mathrm{vol}(M^n,d{\bf x}_2) \cdot \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &= \int_{\mathrm{Herm}_{n}(F)} \,dY \int_{(\mathcal{H}^k)^{n,(n)}} \psi (\langle Y, T({\bf x}_1)-T\rangle)\,d{\bf x}_1\\ &= \beta(\mathcal{H}^k,L). \end{align*}
□
Combining the above two lemmas, we have the following.
Corollary A.10
(1) If
 $L$ is of rank
$L$ is of rank  $1$, then we have
$1$, then we have
 \[ \beta_{1}(M, L,X)=1-X. \]
\[ \beta_{1}(M, L,X)=1-X. \]
(2) If
 $L$ is of rank
$L$ is of rank  $2$, then we have
$2$, then we have
 \[ \beta_{2}(M,L,X)=\begin{cases} (1-X), & \text{if }L=\mathcal{H},\\ (1-X)(1-q^2X), & \text{otherwise}. \end{cases} \]
\[ \beta_{2}(M,L,X)=\begin{cases} (1-X), & \text{if }L=\mathcal{H},\\ (1-X)(1-q^2X), & \text{otherwise}. \end{cases} \]
Lemma A.11 For an ![]() $\mathcal {O}_F$-Hermitian lattice, let
$\mathcal {O}_F$-Hermitian lattice, let ![]() $\bar L= L/\pi L$ be its reduction modulo
$\bar L= L/\pi L$ be its reduction modulo ![]() $\pi$ with resulting quadratic form. Let
$\pi$ with resulting quadratic form. Let ![]() $r(\overline {M},\overline {L})$ to be the number of isometries from
$r(\overline {M},\overline {L})$ to be the number of isometries from ![]() $\overline {L}$ to
$\overline {L}$ to ![]() $\overline {M}$. Then
$\overline {M}$. Then
Proof. The second identity follows from the same proof of [Reference Cho and YamauchiCY20, Theorem 3.12]. Then a similar argument as in the proof of Lemma A.9 gives the first identity. In this case, we need to replace ![]() $M^n{\unicode{x29BA}} (\mathcal {H}^{k})^{n,(n)}$ in the proof of Lemma A.9 with
$M^n{\unicode{x29BA}} (\mathcal {H}^{k})^{n,(n)}$ in the proof of Lemma A.9 with ![]() $M^{n,(n)}{\unicode{x29BA}} (\pi \mathcal {H}^{k})^n$. The factor
$M^{n,(n)}{\unicode{x29BA}} (\pi \mathcal {H}^{k})^n$. The factor ![]() $X^n$ shows up because
$X^n$ shows up because ![]() $\mathrm {vol}((\pi \mathcal {H}^k)^n)=(q^{-2k})^n$. We leave the details to the reader.
$\mathrm {vol}((\pi \mathcal {H}^k)^n)=(q^{-2k})^n$. We leave the details to the reader.
Note that [Reference Li and ZhangLZ22b, Lemma 3.2.1] provides a uniform formula for ![]() $|r(\overline {M},\overline {L})|$. As a result, we obtain the following corollaries.
$|r(\overline {M},\overline {L})|$. As a result, we obtain the following corollaries.
Corollary A.12 Assume ![]() $L=\mathcal {O}_F {\bf x}$ is of rank
$L=\mathcal {O}_F {\bf x}$ is of rank ![]() $1$ (we allow
$1$ (we allow ![]() $q({\bf x}) =0$).
$q({\bf x}) =0$).
(1) If
 $\mathrm {v}(L)=0$, then
$\mathrm {v}(L)=0$, then
 \[ \beta_0(M,L,X)=\begin{cases}
(1+\chi(M) \chi(L)q^{-({m-1})/{2}})X, & \text{if }m\text{
is odd},\\ (1-\chi(M)q^{-{m}/{2}})X, & \text{if }m\text{
is even}. \end{cases} \]
\[ \beta_0(M,L,X)=\begin{cases}
(1+\chi(M) \chi(L)q^{-({m-1})/{2}})X, & \text{if }m\text{
is odd},\\ (1-\chi(M)q^{-{m}/{2}})X, & \text{if }m\text{
is even}. \end{cases} \]
(2) If
 $\mathrm {v}(L)>0$, then
$\mathrm {v}(L)>0$, then
 \[ \beta_0(M,L,X)=\begin{cases}
(1-q^{1-m})X , & \text{if }m\text{ is odd},\\
(1-q^{1-m}+\chi(M)(q-1)q^{-{m}/{2}})X, & \text{if
}m\text{ is even}. \end{cases} \]
\[ \beta_0(M,L,X)=\begin{cases}
(1-q^{1-m})X , & \text{if }m\text{ is odd},\\
(1-q^{1-m}+\chi(M)(q-1)q^{-{m}/{2}})X, & \text{if
}m\text{ is even}. \end{cases} \]
Corollary A.13 Assume ![]() $L$ is of rank
$L$ is of rank ![]() $2$. When
$2$. When ![]() $t(L)=1$, we assume that
$t(L)=1$, we assume that ![]() $L$ has Gram matrix
$L$ has Gram matrix ![]() $T=\mathrm {Diag}(u_1,u_2(-\pi _0)^b)$ with
$T=\mathrm {Diag}(u_1,u_2(-\pi _0)^b)$ with ![]() $b >0$.
$b >0$.
(1) If
 $m$ is odd, then
$m$ is odd, then
 \[ \beta_0(M,L,X)=\begin{cases} q(1-q^{1-m})X^2, & \text{if }t(L)=0,\\ q(1+\chi(M)\chi( u_1)q^{({3-m})/{2}})(1-q^{1-m})X^2, & \text{if }t(L)=1,\\ q(1-q^{1-m})(1-q^{3-m})X^2, & \text{if }t(L)=2. \end{cases} \]
\[ \beta_0(M,L,X)=\begin{cases} q(1-q^{1-m})X^2, & \text{if }t(L)=0,\\ q(1+\chi(M)\chi( u_1)q^{({3-m})/{2}})(1-q^{1-m})X^2, & \text{if }t(L)=1,\\ q(1-q^{1-m})(1-q^{3-m})X^2, & \text{if }t(L)=2. \end{cases} \]
(2) If
 $m$ is even, then
$m$ is even, then
 \[ \beta_0(M,L,X)=\begin{cases} q (
1-\chi(L)q^{1-m} +\chi(L)\chi(M)(q-\chi(L))q^{-{m}/{2}} )
X^2, & \text{if }t(L)=0,\\
q(1-\chi(M)q^{-{m}/{2}})(1-q^{2-m})X^2, & \text{if
}t(L)=1,\\ q ( (1-q^{2-m})+\chi(M)(q^2-1)q^{-{m}/{2}}
)(1-q^{2-m})X^2, & \text{if }t(L)=2. \end{cases}
\]
\[ \beta_0(M,L,X)=\begin{cases} q (
1-\chi(L)q^{1-m} +\chi(L)\chi(M)(q-\chi(L))q^{-{m}/{2}} )
X^2, & \text{if }t(L)=0,\\
q(1-\chi(M)q^{-{m}/{2}})(1-q^{2-m})X^2, & \text{if
}t(L)=1,\\ q ( (1-q^{2-m})+\chi(M)(q^2-1)q^{-{m}/{2}}
)(1-q^{2-m})X^2, & \text{if }t(L)=2. \end{cases}
\]
Finally, we calculate ![]() $\beta _1(M,L,X)$.
$\beta _1(M,L,X)$.
Proposition A.14 Assume ![]() $L$ is as in Corollary A.13. Let
$L$ is as in Corollary A.13. Let ![]() $\delta _e(m)=1$ or
$\delta _e(m)=1$ or ![]() $0$ depending on whether
$0$ depending on whether ![]() $m$ is even or odd.
$m$ is even or odd.
(1) If
 $t(L)=2$, then
$t(L)=2$, then
 \[ \beta_1(M,L,X)= q(q+1) (
(1-q^{1-m})+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}
)X(1-X). \]
\[ \beta_1(M,L,X)= q(q+1) (
(1-q^{1-m})+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}
)X(1-X). \]
(2) If
 $t(L)=1$, then
$t(L)=1$, then
 \[ \beta_1(M,L,X) =\begin{cases}
q(1+q-q^{1-m}+\chi(M)\chi( u_1)q^{({3-m})/{2}})X(1-X), &
\text{if }m\text{ is odd},\\
q(1+q-q^{1-m}-\chi(M)q^{-{m}/{2}})X(1-X), & \text{if
}m\text{ is even}. \end{cases} \]
\[ \beta_1(M,L,X) =\begin{cases}
q(1+q-q^{1-m}+\chi(M)\chi( u_1)q^{({3-m})/{2}})X(1-X), &
\text{if }m\text{ is odd},\\
q(1+q-q^{1-m}-\chi(M)q^{-{m}/{2}})X(1-X), & \text{if
}m\text{ is even}. \end{cases} \]
(3) If
 $t(L)=0$ and
$t(L)=0$ and  $\chi (L)=1$, i.e.
$\chi (L)=1$, i.e.  $L\cong \mathcal {H}_0$, then
$L\cong \mathcal {H}_0$, then
 \[ \beta_1(M,L,X)= q (
q+1-2q^{1-m}+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}
)X(1-X). \]
\[ \beta_1(M,L,X)= q (
q+1-2q^{1-m}+\delta_{e}(m)\chi(M)(q-1)q^{-{m}/{2}}
)X(1-X). \]
(4) If
 $t(L)=0$ and
$t(L)=0$ and  $\chi (L)=-1$, then
$\chi (L)=-1$, then
 \[ \beta_1(M,L,X)= q (q+1) (
1-\delta_{e}(m)\chi(M)q^{-{m}/{2}} )X(1-X).
\]
\[ \beta_1(M,L,X)= q (q+1) (
1-\delta_{e}(m)\chi(M)q^{-{m}/{2}} )X(1-X).
\]
Proof. First we assume ![]() $L=\mathcal {H}_i$. We claim that
$L=\mathcal {H}_i$. We claim that
 \[ \beta_1(M, \mathcal{H}_i, X) =\begin{cases} q(1-X)\biggl(2\beta_0(M,0,X)+\displaystyle\sum_{\alpha \in (\mathcal{O}_{F_0}/(\pi_0))^{\times}}\beta_0(M, \langle -2\alpha \rangle,X) \biggr), & \text{if }i=0,\\ q(q+1) (1-X)\beta_0(M,0,X), & \text{if }i\ge 1. \end{cases} \]
\[ \beta_1(M, \mathcal{H}_i, X) =\begin{cases} q(1-X)\biggl(2\beta_0(M,0,X)+\displaystyle\sum_{\alpha \in (\mathcal{O}_{F_0}/(\pi_0))^{\times}}\beta_0(M, \langle -2\alpha \rangle,X) \biggr), & \text{if }i=0,\\ q(q+1) (1-X)\beta_0(M,0,X), & \text{if }i\ge 1. \end{cases} \]
Here ![]() $\alpha (M, 0, X)=\alpha (M, \mathcal {O}_F {\bf x}, X)$ with
$\alpha (M, 0, X)=\alpha (M, \mathcal {O}_F {\bf x}, X)$ with ![]() $q({\bf x}) =0$ and
$q({\bf x}) =0$ and ![]() ${\bf x} \ne 0$. Assuming the claim, the proposition for
${\bf x} \ne 0$. Assuming the claim, the proposition for ![]() $L=\mathcal {H}_i$ follows from Corollary A.12.
$L=\mathcal {H}_i$ follows from Corollary A.12.
To prove the claim, it suffices to show the identity for ![]() $X=q^{-2k}$ for sufficiently many
$X=q^{-2k}$ for sufficiently many ![]() $k\ge 0$. Recall
$k\ge 0$. Recall
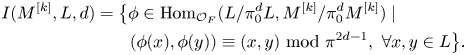 \begin{align*} I(M^{[k]},L,d)&=\big\{
\phi \in \mathrm{Hom}_{\mathcal{O}_F}(L/\pi_0^d L, M^{[k]}/
\pi_0^d M^{[k]}) \mid\\ &\qquad (\phi(x),\phi(y))\equiv(x,y) \text{ mod } \pi^{2d-1},\
\forall x,y \in L\big\}. \end{align*}
\begin{align*} I(M^{[k]},L,d)&=\big\{
\phi \in \mathrm{Hom}_{\mathcal{O}_F}(L/\pi_0^d L, M^{[k]}/
\pi_0^d M^{[k]}) \mid\\ &\qquad (\phi(x),\phi(y))\equiv(x,y) \text{ mod } \pi^{2d-1},\
\forall x,y \in L\big\}. \end{align*}
Let
Then
Let ![]() $\{l_1,l_2\}$ be a basis of
$\{l_1,l_2\}$ be a basis of ![]() $L$ with Gram matrix
$L$ with Gram matrix ![]() $\mathcal {H}_i$. For
$\mathcal {H}_i$. For ![]() $\phi \in J(M^{[k]},L,d)$, it will be determined by
$\phi \in J(M^{[k]},L,d)$, it will be determined by ![]() $w_i=\phi (l_i)$. Let
$w_i=\phi (l_i)$. Let ![]() $w_{i,\mathcal {H}}=\mathrm {Pr}_{\mathcal {H}^k}(w_i)$, and
$w_{i,\mathcal {H}}=\mathrm {Pr}_{\mathcal {H}^k}(w_i)$, and ![]() $w_{i,M}=\mathrm {Pr}_{M}(w_i)$. Since
$w_{i,M}=\mathrm {Pr}_{M}(w_i)$. Since ![]() $\mathrm {rank}_{\mathbb {F}_{q}}\overline {\mathrm {Pr}_{\mathcal {H}^k}(\phi (L))}=1$,
$\mathrm {rank}_{\mathbb {F}_{q}}\overline {\mathrm {Pr}_{\mathcal {H}^k}(\phi (L))}=1$, ![]() $\mathrm {rank}_{\mathbb {F}_{q}}\overline {\mathrm {Pr}_{\mathcal {H}^k}(w_i)}=1$ for
$\mathrm {rank}_{\mathbb {F}_{q}}\overline {\mathrm {Pr}_{\mathcal {H}^k}(w_i)}=1$ for ![]() $i=1$ or
$i=1$ or ![]() $2$.
$2$.
Now we define a partition of ![]() $J(M^{[k]},L,d)$. Assume
$J(M^{[k]},L,d)$. Assume ![]() $\alpha \in \mathcal {O}_{F_0}$. Let
$\alpha \in \mathcal {O}_{F_0}$. Let
 \begin{align*}
J_{\alpha}(M^{[k]},L,d)&:= \{\phi\in
I(M^{[k]},L,d)\mid
\mathrm{rank}_{\mathbb{F}_{q}}\overline{w}_{1,\mathcal{H}}
=1,\ \overline{w}_{2,\mathcal{H}}=\alpha
\overline{w}_{1,\mathcal{H}}\},\\
J_{\infty}(M^{[k]},L,d)&:= \{\phi\in
I(M^{[k]},L,d)\mid
\mathrm{rank}_{\mathbb{F}_{q}}\overline{w}_{2,\mathcal{H}}=1,\
\overline{w}_{1,\mathcal{H}}=0 \}.
\end{align*}
\begin{align*}
J_{\alpha}(M^{[k]},L,d)&:= \{\phi\in
I(M^{[k]},L,d)\mid
\mathrm{rank}_{\mathbb{F}_{q}}\overline{w}_{1,\mathcal{H}}
=1,\ \overline{w}_{2,\mathcal{H}}=\alpha
\overline{w}_{1,\mathcal{H}}\},\\
J_{\infty}(M^{[k]},L,d)&:= \{\phi\in
I(M^{[k]},L,d)\mid
\mathrm{rank}_{\mathbb{F}_{q}}\overline{w}_{2,\mathcal{H}}=1,\
\overline{w}_{1,\mathcal{H}}=0 \}.
\end{align*}
Then it is easy to verify
Now we compute ![]() $|J_{\alpha }(M^{[k]},L,d)|$. To determine a
$|J_{\alpha }(M^{[k]},L,d)|$. To determine a ![]() $\phi \in J_{\alpha }(M^{[k]},L,d)$, we choose
$\phi \in J_{\alpha }(M^{[k]},L,d)$, we choose ![]() $w_1=\phi (l_1)$ first. By definition, we have
$w_1=\phi (l_1)$ first. By definition, we have
 \begin{align} & \lim_{d\to \infty}q^{(2(2k+m)-1)d}\#\big\{w_1\in M^{[k]}/\pi_0^d M^{[k]} \mid w_{1,\mathcal{H}}\text{ is primitive, and } q(w_1)\equiv 0 \text{ mod } \pi_0^d \big\}\nonumber\\ &\qquad=\beta_1(M^{[k]},0)=1-q^{-2k}. \end{align}
\begin{align} & \lim_{d\to \infty}q^{(2(2k+m)-1)d}\#\big\{w_1\in M^{[k]}/\pi_0^d M^{[k]} \mid w_{1,\mathcal{H}}\text{ is primitive, and } q(w_1)\equiv 0 \text{ mod } \pi_0^d \big\}\nonumber\\ &\qquad=\beta_1(M^{[k]},0)=1-q^{-2k}. \end{align} Given such a ![]() $w_1$, now we find the number of
$w_1$, now we find the number of ![]() $w_2=\phi (l_2)$ such that
$w_2=\phi (l_2)$ such that ![]() $\phi$ lies in
$\phi$ lies in ![]() $J_{\alpha }(M^{[k]},L,d)$. By Lemma A.2, we may assume
$J_{\alpha }(M^{[k]},L,d)$. By Lemma A.2, we may assume ![]() $w_{1,S}=0$. Let
$w_{1,S}=0$. Let ![]() $w_2=w_{2,M}+\alpha w_1+\pi w_\mathcal {H}$, where
$w_2=w_{2,M}+\alpha w_1+\pi w_\mathcal {H}$, where ![]() $w_\mathcal {H}\in \mathcal {H}^k$. Then the corresponding
$w_\mathcal {H}\in \mathcal {H}^k$. Then the corresponding ![]() $\phi$ lies in
$\phi$ lies in ![]() $J_{\alpha }(M^{[k]},L,d)$ if and only if
$J_{\alpha }(M^{[k]},L,d)$ if and only if
and
 \begin{align*} 0\equiv q(w_2)&\equiv\mathrm{tr}((\alpha w_1,\pi w_\mathcal{H}))-\pi_0 q(w_\mathcal{H})+q(w_{2,M}) \\ &\equiv\alpha\mathrm{tr}(\pi^i)-\pi_0 q(w_\mathcal{H})+q(w_{2,M}) \mod \pi^{2d-1}. \end{align*}
\begin{align*} 0\equiv q(w_2)&\equiv\mathrm{tr}((\alpha w_1,\pi w_\mathcal{H}))-\pi_0 q(w_\mathcal{H})+q(w_{2,M}) \\ &\equiv\alpha\mathrm{tr}(\pi^i)-\pi_0 q(w_\mathcal{H})+q(w_{2,M}) \mod \pi^{2d-1}. \end{align*}
First,
Second, for each fixed ![]() $\pi w_\mathcal {H}$ we have
$\pi w_\mathcal {H}$ we have
 \begin{align} &\lim_{d\to
\infty}q^{(-2m+1)d} \#\{ w_{2,M} \in M/\pi_0^d M\mid
w_{2,M} \text{ primitive, } q(w_{2,M})\equiv -\alpha
\mathrm{tr}(\pi^i)+\pi_0 q(w_\mathcal{H})\ \text{mod } \pi_0^d\} \nonumber\\ &\qquad =\beta(M,\langle
-\alpha \mathrm{tr}(\pi^i)+\pi_0
q(w_\mathcal{H})\rangle)\nonumber\\ &\qquad =\begin{cases}
\beta(M, \langle -2 \alpha \rangle), & \text{if } i=0,\\
\beta(M, 0), & \text{if } i > 0. \end{cases}
\end{align}
\begin{align} &\lim_{d\to
\infty}q^{(-2m+1)d} \#\{ w_{2,M} \in M/\pi_0^d M\mid
w_{2,M} \text{ primitive, } q(w_{2,M})\equiv -\alpha
\mathrm{tr}(\pi^i)+\pi_0 q(w_\mathcal{H})\ \text{mod } \pi_0^d\} \nonumber\\ &\qquad =\beta(M,\langle
-\alpha \mathrm{tr}(\pi^i)+\pi_0
q(w_\mathcal{H})\rangle)\nonumber\\ &\qquad =\begin{cases}
\beta(M, \langle -2 \alpha \rangle), & \text{if } i=0,\\
\beta(M, 0), & \text{if } i > 0. \end{cases}
\end{align}
By symmetry, ![]() $| J_{\infty }(M^{[k]},L,d)|=| J_{0}(M^{[k]},L,d)|$. Now a combination of (A.6), (A.7) and (A.8) implies that
$| J_{\infty }(M^{[k]},L,d)|=| J_{0}(M^{[k]},L,d)|$. Now a combination of (A.6), (A.7) and (A.8) implies that
 \begin{align*} \beta_1(M, \mathcal{H}_i, q^{-2k}) &=\lim_{d\to \infty}q^{(-4(2k+m)+4)d} \biggl(\sum_{\alpha\in \mathcal{O}_{F_0}/(\pi_0)}| J_{\alpha}(M^{[k]},L,d)|+| J_{\infty}(M^{[k]},L,d)|\biggr)\\ &=\begin{cases} q(1-X)\biggl(2\beta_0(M,0,q^{-2k})+\displaystyle\sum_{\alpha \in \mathcal{O}_{F_0}^{\times}/(\pi_0)}\beta_0(M,-2\alpha,q^{-2k}) \biggr), & \text{if }i=0,\\ q(q+1) (1-X)\beta_0(M,0,q^{-2k}), & \text{if }i\ge 1, \end{cases} \end{align*}
\begin{align*} \beta_1(M, \mathcal{H}_i, q^{-2k}) &=\lim_{d\to \infty}q^{(-4(2k+m)+4)d} \biggl(\sum_{\alpha\in \mathcal{O}_{F_0}/(\pi_0)}| J_{\alpha}(M^{[k]},L,d)|+| J_{\infty}(M^{[k]},L,d)|\biggr)\\ &=\begin{cases} q(1-X)\biggl(2\beta_0(M,0,q^{-2k})+\displaystyle\sum_{\alpha \in \mathcal{O}_{F_0}^{\times}/(\pi_0)}\beta_0(M,-2\alpha,q^{-2k}) \biggr), & \text{if }i=0,\\ q(q+1) (1-X)\beta_0(M,0,q^{-2k}), & \text{if }i\ge 1, \end{cases} \end{align*}
as claimed.
Next, we assume ![]() $L$ has a basis
$L$ has a basis ![]() $\{ l_1, l_2\}$ whose Gram matrix is
$\{ l_1, l_2\}$ whose Gram matrix is ![]() $\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with
$\mathrm {Diag}(u_1(-\pi _0)^a,u_2(-\pi _0)^b)$ with ![]() $0 \le a \le b$. Let
$0 \le a \le b$. Let ![]() $w_i=\phi (l_i)$ as before. Then the number of possible choices for
$w_i=\phi (l_i)$ as before. Then the number of possible choices for ![]() $w_1$ is given by
$w_1$ is given by
for sufficiently large ![]() $d$. We may assume
$d$. We may assume ![]() $w_1=w_{1,\mathcal {H}}$ without loss of generality. Let
$w_1=w_{1,\mathcal {H}}$ without loss of generality. Let ![]() $w_2=w_{2,M}+\alpha w_1+\pi w_\mathcal {H}$ as before. Then
$w_2=w_{2,M}+\alpha w_1+\pi w_\mathcal {H}$ as before. Then ![]() $\phi$ lies in
$\phi$ lies in ![]() $J_{\alpha }(M^{[k]},L,d)$ if and only if
$J_{\alpha }(M^{[k]},L,d)$ if and only if
and
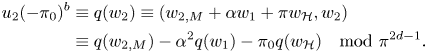 \begin{align*} u_2(-\pi_0)^b&\equiv q(w_2)\equiv(w_{2,M}+\alpha w_{1}+\pi w_\mathcal{H} , w_2)\\ &\equiv q(w_{2,M})-\alpha^2 q( w_1)-\pi_0 q(w_\mathcal{H})\mod \pi^{2d-1}. \end{align*}
\begin{align*} u_2(-\pi_0)^b&\equiv q(w_2)\equiv(w_{2,M}+\alpha w_{1}+\pi w_\mathcal{H} , w_2)\\ &\equiv q(w_{2,M})-\alpha^2 q( w_1)-\pi_0 q(w_\mathcal{H})\mod \pi^{2d-1}. \end{align*}
Now
and for a fixed ![]() $\pi w_\mathcal {H}$ we have
$\pi w_\mathcal {H}$ we have
 \begin{align*}
&\lim_{d\to \infty}q^{(-2m+1)d} \#\bigl\{ w_{2,M} \in L_{S}/\pi_0^d
L_{S}\mid w_{2,M} \text{ primitive},\\ & q(w_{2,M})\equiv u_2(-\pi_0)^b+\alpha^2 q( w_1)+\pi_0
q(w_\mathcal{H})\ \text{mod}\ \pi^{2d-1}\bigr\}\\
&\quad=\beta(M, \langle u_2(-\pi_0)^b+\alpha^2 q(
w_1)+\pi_0 q(w_\mathcal{H})\rangle).
\end{align*}
\begin{align*}
&\lim_{d\to \infty}q^{(-2m+1)d} \#\bigl\{ w_{2,M} \in L_{S}/\pi_0^d
L_{S}\mid w_{2,M} \text{ primitive},\\ & q(w_{2,M})\equiv u_2(-\pi_0)^b+\alpha^2 q( w_1)+\pi_0
q(w_\mathcal{H})\ \text{mod}\ \pi^{2d-1}\bigr\}\\
&\quad=\beta(M, \langle u_2(-\pi_0)^b+\alpha^2 q(
w_1)+\pi_0 q(w_\mathcal{H})\rangle).
\end{align*}
Now this proposition follows from a similar argument as before, and we leave the details to the reader.