Article contents
The Kodaira dimension of complex hyperbolic manifolds with cusps
Published online by Cambridge University Press: 28 November 2017
Abstract
We prove a bound relating the volume of a curve near a cusp in a complex ball quotient 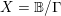 $X=\mathbb{B}/\unicode[STIX]{x1D6E4}$ to its multiplicity at the cusp. There are a number of consequences: we show that for an
$X=\mathbb{B}/\unicode[STIX]{x1D6E4}$ to its multiplicity at the cusp. There are a number of consequences: we show that for an  $n$-dimensional toroidal compactification
$n$-dimensional toroidal compactification 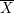 $\overline{X}$ with boundary
$\overline{X}$ with boundary 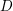 $D$,
$D$, 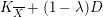 $K_{\overline{X}}+(1-\unicode[STIX]{x1D706})D$ is ample for
$K_{\overline{X}}+(1-\unicode[STIX]{x1D706})D$ is ample for 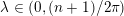 $\unicode[STIX]{x1D706}\in (0,(n+1)/2\unicode[STIX]{x1D70B})$, and in particular that
$\unicode[STIX]{x1D706}\in (0,(n+1)/2\unicode[STIX]{x1D70B})$, and in particular that 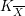 $K_{\overline{X}}$ is ample for
$K_{\overline{X}}$ is ample for 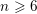 $n\geqslant 6$. By an independent algebraic argument, we prove that every ball quotient of dimension
$n\geqslant 6$. By an independent algebraic argument, we prove that every ball quotient of dimension 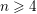 $n\geqslant 4$ is of general type, and conclude that the phenomenon famously exhibited by Hirzebruch in dimension 2 does not occur in higher dimensions. Finally, we investigate the applications to the problem of bounding the number of cusps and to the Green–Griffiths conjecture.
$n\geqslant 4$ is of general type, and conclude that the phenomenon famously exhibited by Hirzebruch in dimension 2 does not occur in higher dimensions. Finally, we investigate the applications to the problem of bounding the number of cusps and to the Green–Griffiths conjecture.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 4
- Cited by


