Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cellarosi, Francesco
and
Marklof, Jens
2016.
Quadratic Weyl sums, automorphic functions and invariance principles.
Proceedings of the London Mathematical Society,
Vol. 113,
Issue. 6,
p.
775.
Vogt, Trenton
and
Ulness, Darin J.
2019.
Cornu Spirals and the Triangular Lacunary Trigonometric System.
Fractal and Fractional,
Vol. 3,
Issue. 3,
p.
40.
Lamzouri, Youness
2020.
ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 4,
p.
1259.
Chen, Changhao
and
Shparlinski, Igor E.
2021.
Small values of Weyl sums.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 2,
p.
124743.
Autissier, Pascal
Bonolis, Dante
and
Lamzouri, Youness
2021.
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions.
Compositio Mathematica,
Vol. 157,
Issue. 7,
p.
1610.
Granville, Andrew
and
Lamzouri, Youness
2021.
Large deviations of sums of random variables.
Lithuanian Mathematical Journal,
Vol. 61,
Issue. 3,
p.
345.
BONOLIS, DANTE
2022.
On the size of the maximum of incomplete Kloosterman sums.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 172,
Issue. 3,
p.
563.
Hussain, Ayesha
2022.
The Limiting Distribution of Character Sums.
International Mathematics Research Notices,
Vol. 2022,
Issue. 20,
p.
16292.
Milićević, Djordje
and
Zhang, Sichen
2023.
Distribution of Kloosterman paths to high prime power moduli.
Transactions of the American Mathematical Society, Series B,
Vol. 10,
Issue. 20,
p.
636.
Cellarosi, Francesco
Griffin, Jory
and
Osman, Tariq
2023.
Improved tail estimates for the distribution of quadratic Weyl sums.
Bollettino dell'Unione Matematica Italiana,
Vol. 16,
Issue. 2,
p.
203.
Hussain, Ayesha
and
Lamzouri, Youness
2024.
The limiting distribution of Legendre paths.
Journal de l’École polytechnique — Mathématiques,
Vol. 11,
Issue. ,
p.
589.
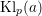 $\text{Kl}_{p}(a)$, as
$\text{Kl}_{p}(a)$, as  $a$ varies over
$a$ varies over 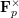 $\mathbf{F}_{p}^{\times }$ and as
$\mathbf{F}_{p}^{\times }$ and as 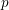 $p$ tends to infinity. Using independence of Kloosterman sheaves, we prove convergence in the sense of finite distributions to a specific random Fourier series. We also consider Birch sums, for which we can establish convergence in law in the space of continuous functions. We then derive some applications.
$p$ tends to infinity. Using independence of Kloosterman sheaves, we prove convergence in the sense of finite distributions to a specific random Fourier series. We also consider Birch sums, for which we can establish convergence in law in the space of continuous functions. We then derive some applications.

