Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T09:41:33.708Z Has data issue: false hasContentIssue false
  • English
  • Français

K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant

Part of: Partial differential equations on manifolds; differential operators Surfaces and higher-dimensional varieties Discontinuous groups and automorphic forms Curves

Published online by Cambridge University Press:  19 November 2020

Shouhei Ma  and
Ken-Ichi Yoshikawa
Shouhei Ma
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, Tokyo152-8551, [email protected]
Ken-Ichi Yoshikawa
Affiliation:
Faculty of Science, Department of Mathematics, Kyoto University, Kyoto606-8502, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Yoshikawa in [Invent. Math. 156 (2004), 53–117] introduces a holomorphic torsion invariant of 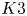$K3$ surfaces with involution. In this paper we completely determine its structure as an automorphic function on the moduli space of such 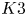$K3$ surfaces. On every component of the moduli space, it is expressed as the product of an explicit Borcherds lift and a classical Siegel modular form. We also introduce its twisted version. We prove its modularity and a certain uniqueness of the modular form corresponding to the twisted holomorphic torsion invariant. This is used to study an equivariant analogue of Borcherds’ conjecture.

Keywords

K3 surfacesanalytic torsionBorcherds productstheta constants

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables) 14H45: Special curves and curves of low genus 14J28: $K3$ surfaces and Enriques surfaces 58J52: Determinants and determinant bundles, analytic torsion
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 10 , October 2020 , pp. 1965 - 2019
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexeev, V. and Nikulin, V. V., Del Pezzo and K3 surfaces, MSJ Memoires, vol. 15 (Mathematical Society of Japan, 2006).CrossRefGoogle Scholar
Alvarez-Gaumé, L., Moore, G. and Vafa, C., Theta functions, modular invariance, and strings, Commun. Math. Phys. 106 (1986), 1–40.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of algebraic curves, I (Springer, Berlin, 1985).CrossRefGoogle Scholar
Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A., Compact complex surfaces, second edition (Springer, Berlin, 2004).CrossRefGoogle Scholar
Bershadsky, M., Cecotti, S., Ooguri, H. and Vafa, C., Kodaira-Spencer theory of gravity and exact results for quantum string amplitudes, Commun. Math. Phys. 165 (1994), 311–427.CrossRefGoogle Scholar
Bismut, J.-M., Equivariant immersions and Quillen metrics, J. Differential Geom. 41 (1995), 53–157.CrossRefGoogle Scholar
Bismut, J.-M., Gillet, H. and Soulé, C., Analytic torsion and holomorphic determinant bundles I, II, III, Commun. Math. Phys. 115 (1988), 49–78, 79–126, 301–351.CrossRefGoogle Scholar
Borcherds, R. E., Automorphic forms with singularities on Grassmanians, Invent. Math. 132 (1998), 491–562.CrossRefGoogle Scholar
Borcherds, R. E., Reflection groups of Lorentzian lattices, Duke Math. J. 104 (2000), 319–366.CrossRefGoogle Scholar
Borcherds, R. E., Katzarkov, L., Pantev, T. and Shepherd-Barron, N. I., Families of $K3$ surfaces, J. Algebraic Geom. 7 (1998), 183–193.Google Scholar
Borel, A., Some metric properties of arithmetic quotients of symmetric spaces and an extension theorem, J. Differential Geom. 6 (1972), 543–560.CrossRefGoogle Scholar
Bost, J.-B. and Nelson, P., Spin-$\frac {1}{2}$ bosonization on compact surfaces, Phys. Rev. Lett. 57 (1986), 795–798.CrossRefGoogle ScholarPubMed
Fang, H., Lu, Z. and Yoshikawa, K.-I., Analytic torsion for Calabi–Yau threefolds, J. Differential Geom. 80 (2008), 175–259.CrossRefGoogle Scholar
Fay, J., Kernel functions, analytic torsion, and moduli spaces, Mem. Amer. Math. Soc. 464 (1992).Google Scholar
Finashin, S. and Kharlamov, V., Deformation classes of real four-dimensional cubic hypersurfaces, J. Algebraic Geom. 17 (2008), 677–707.CrossRefGoogle Scholar
Fontanari, C. and Pascolutti, S., An affine open covering of ${\mathcal {M}}_{g}$ for $g\leq 5$, Geom. Dedicata 158 (2012), 61–68.CrossRefGoogle Scholar
Gillet, H. and Soulé, C., An arithmetic Riemann-Roch theorem, Invent. Math. 110 (1992), 473–543.CrossRefGoogle Scholar
Gross, M. and Wilson, P. M. H., Mirror symmetry via $3$-tori for a class of Calabi-Yau threefolds, Math. Ann. 309 (1997), 505–531.CrossRefGoogle Scholar
Grothenidieck, A., Éléments de géométrie algébrique: II, Publ. Math. Inst. Hautes Etudes Sci. 8 (1961), 5–222.Google Scholar
Grushevsky, S. and Salvati-Manni, R., The superstring cosmological constant and the Schottky form in genus $5$, Amer. J. Math. 133 (2011), 1007–1027.CrossRefGoogle Scholar
Igusa, J.-I., Modular forms and projective invariants, Amer. J. Math. 89 (1967), 817–855.CrossRefGoogle Scholar
Igusa, J.-I., Theta functions (Springer, Berlin, 1972).CrossRefGoogle Scholar
Igusa, J.-I., On the irreducibility of Schottky's divisor, J. Fac. Sci. Univ. Tokyo 28 (1982), 531–545.Google Scholar
Kondō, S., The rationality of the moduli space of Enriques surfaces, Compositio Math. 91 (1994), 159–173.Google Scholar
Ma, S., Rationality of the moduli spaces of $2$-elementary $K3$ surfaces, J. Algebraic Geom. 24 (2015), 81–158.CrossRefGoogle Scholar
Ma, X., Submersions and equivariant Quillen metrics, Ann. Inst. Fourier 50 (2000), 1539–1588.CrossRefGoogle Scholar
Ma, X., Orbifolds and analytic torsions, Trans. Amer. Math. Soc. 357 (2005), 2205–2233.CrossRefGoogle Scholar
Maillot, V. and Rössler, D., Formes automorphes et théorèmes de Riemann–Roch arithmétiques, Astérisque 328 (2009), 233–249.Google Scholar
Martens, G. and Schreyer, F.-O., Line bundles and syzygies of trigonal bundles, Abh. Math. Semin. Univ. Hambg. 86 (1986), 169–189.CrossRefGoogle Scholar
Mayer, A. L., Families of $K3$ surfaces, Nagoya Math. J. 48 (1972), 1–17.CrossRefGoogle Scholar
Mumford, D., Fogarty, J. and Kirwan, F. C., Geometric invariant theory, third edition (Springer, Berlin, 1994).CrossRefGoogle Scholar
Nikulin, V. V., Integral symmetric bilinear forms and some of their applications, Math. USSR Izv. 14 (1980), 103–167.CrossRefGoogle Scholar
Nikulin, V. V., Factor groups of groups of automorphisms of hyperbolic forms with respect to subgroups generated by $2$-reflections, J. Soviet Math. 22 (1983), 1401–1476.CrossRefGoogle Scholar
Ray, D. B. and Singer, I. M., Analytic torsion for complex manifolds, Ann. Math. 98 (1973), 154–177.CrossRefGoogle Scholar
Saint-Donat, B., Projective models of $K3$ surfaces, Amer. J. Math. 96 (1974), 602–639.CrossRefGoogle Scholar
Scattone, F., On the compactification of moduli spaces for algebraic $K3$ surfaces, Mem. Amer. Math. Soc. 70 (1987), 374.Google Scholar
Scheithauer, N. R., On the classification of automorphic products and generalized Kac–Moody algebras, Invent. Math. 164 (2006), 641–678.CrossRefGoogle Scholar
Schofer, J., Borcherds forms and generalizations of singular moduli, J. Reine Angew. Math. 629 (2009), 1–36.CrossRefGoogle Scholar
Shah, J., A complete moduli space for $K3$ surfaces of degree $2$, Ann. Math. 112 (1980), 485–510.CrossRefGoogle Scholar
Skoruppa, N.-P., Jacbi forms of critical weight and Weil representations, in Modular forms on Schiermonnikoog (Cambridge University Press, Cambridge, 2008), 239–266.CrossRefGoogle Scholar
Teixidor i Bigas, M., The divisor of curves with a vanishing theta-null, Compo. Math. 66 (1988), 15–22.Google Scholar
Tsuyumine, S., Thetanullwerte on a moduli space of curves and hyperelliptic loci, Math. Zeit. 207 (1991), 539–568.CrossRefGoogle Scholar
Wentworth, R. A., Gluing formulas for determinants of Dolbeault Laplacians on Riemann surfaces, Commun. Anal. Geom. 20 (2012), 455–499.CrossRefGoogle Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation, I, Commun. Pure Appl. Math. 31 (1978), 339–411.CrossRefGoogle Scholar
Yoshikawa, K.-I., $K3$ surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space, Invent. Math. 156 (2004), 53–117.CrossRefGoogle Scholar
Yoshikawa, K.-I., Real $K3$ surfaces without real points, equivariant determinant of the Laplacian, and the Borcherds $\Phi$-function, Math. Zeit. 258 (2008), 213–225.CrossRefGoogle Scholar
Yoshikawa, K.-I., $K3$ surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space III, Math. Zeit. 272 (2012), 175–190.CrossRefGoogle Scholar
Yoshikawa, K.-I., $K3$ surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space II, J. Reine Angew. Math. 677 (2013), 15–70.Google Scholar
Yoshikawa, K.-I., Analytic torsion for Borcea-Voisin threefolds, in Geometry, analysis and probability: in honor of Jean-Michel Bismut, Progress in Mathematics, vol. 310, eds. Bost, J.-B., Hofer, H., Labourie, F., Le Jan, Y., Ma, X. and Zhang, W. (Birkhäuser, Cham, 2017), 279–361.CrossRefGoogle Scholar